超越方程的全局优化解法

夏绿玉

(铜陵职业技术学院，安徽 铜陵 244000)



超越方程的全局优化解法

夏绿玉

(铜陵职业技术学院，安徽 铜陵 244000)

现有的粒子群算法在求解超越方程时具有局部搜索能力差、后期收敛速度较慢的缺陷，导致了粒子群算法无法得到较为精确的超越方程的根。在粒子群算法的基础上，加入局部搜索能力较好、后期收敛速度较快的拟牛顿算法，依照算法的进程自动甄选粒子群算法和拟牛顿算法，充分发挥粒子群算法的全局搜索性能和拟牛顿法的局部搜索性能，进而将超越方程转化为了纯粹的函数优化问题，并基于此方法进行求解实验，结果表明该方法具有极高的收敛速度和求解精度。

粒子群算法；全局优化；拟牛顿法；超越方程

超越方程是数学、工程实践中广泛存在的棘手问题，但五次及以上方程并没有根式解，只能使用数值解法进行求解。传统的数值方法种类繁杂：对分法、单形调优法、复形调优法、弦截法等[1-2]。但这些方法受方程本身特性的影响较为严重，不同的初值会得到不同结果，通用性较差、精度较低。需要科研人员根据以往的经验针对具体的问题选择适用的方法，其主观性较强，不适合工程实际中的大范围推广与应用。

20世纪90年代，Kennedy等[3]提出了粒子群(Particle Swarm Optimization，简称PSO)算法，该算法在求解超越方程时可以很好地探寻超越方程的根。Particle Swarm Optimization的通用性较好、迭代格式较为简单，对于连续性、非连续性问题具有很好的适用性，也是一种方便掌握的数学工具[4]，但是，Particle Swarm Optimization在后期收敛之时耗时较多，且收敛效果较差，不能够很好地收敛至较小的范围[5-6]。拟牛顿法(Quasi-Newton Methods)是一种迭代算法，是求解非线性优化问题最有效的方法之一，于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon提出。

本文糅合了Quasi-Newton Methods和Particle Swarm Optimization的优点，提出全局优化解法(Global Optimization Solution)，充分发挥粒子群算法的全局搜索性能和拟牛顿法的局部搜索性能，进而将超越方程转化为了纯粹的函数优化问题，并利用C++开发计算程序，与传统的计算方法相比较，验证Global Optimization Solution的全局搜索能力与局部搜索能力。

1　问题描述

有一超越方程

f(x)=0,

(1)

全部的实数根位于(a,b)中，可以将式(1)转化为

g(x)=f(x)2，

(2)

式(2)在[a,b]区间内的极小值点便是式(1)在(a,b)区间内的根，当g(x)的最小值为0时，所对应的x就是式(1)的根。

2　全局优化算法描述

拟牛顿法是一种收敛性很强的算法，具体做法如下：取X=(x0,y0,R)，假设(x0,y0,R)第i次迭代的值为

(3)

则第i+1次迭代的值为

X(i+1)=(x0,y0,R)(i)-(f0(X(i))+f1(X(i))+f2(X(i)))TF(X(i))-1。

(4)

其中

(5)

令δ(i)=F(X(i))-1(f0(X(i))+f1(X(i))+f2(X(i)))T，

(6)

δ(i)=(δ(i)(x0),δ(i)(y0),δ(i)(R))T，

则有

(7)

由此，我们给定一个精度和初值

(8)

一直迭代，当

|max(f0(X(i))+f1(X(i))+f2(X(i)))T|<ε，

(9)

时便得结果

(10)

此后，将拟牛顿法嵌入粒子群算法中，具体做法如下：

1)初始化粒子群，假设粒子群的种群规模为N，定义随机位置，取k=0；

2)对粒子群中的每一个粒子计算其适应度的值pi；

3)将当下计算的粒子适应度的值pi与粒子历史上适应度最好的位置pbi进行比较，如果pi比pbi更好，则将其作为当前的最好位置；

4)将当下计算的粒子适应度的值pi与粒子全局适应度最好的位置pgi进行比较，如果pi比pgi更好，则将其作为全局的最好位置；

5)对粒子速度和位置进行更新，更新方法如下：

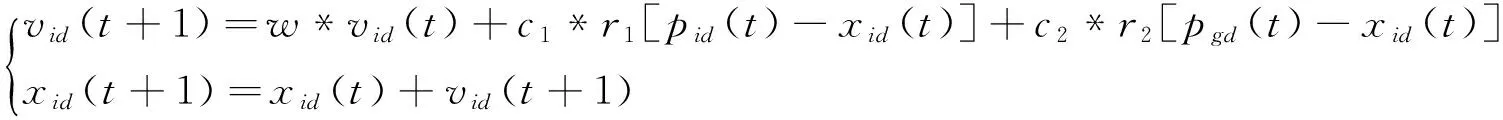
(11)

其中，1≤i≤N并且1≤d≤D；

6)当达到最大的代数M，找出当前全局最优个体pg，进行下一步，如果未达到最大的代数M，令k=k+1，重新进入步骤2)；

7)进行式(3)和式(10)的计算；

8)输出结果。

3　数值计算

利用上述思想，编制GlobalOptimizationSolution的C+ +程序GOS，利用GOS进行计算。

3.1全局搜索

算例1：求解x44+x+1=0的根，见表1。

表1　x44+x+1=0的根

根据基础的数学知识可知，x44+x+1=0共有44个根，通过表1可知，GlobalOptimizationSolution搜索出了44个根，说明GlobalOptimizationSolution的全局搜索能力较佳。

算例2：求解27-18x+2x2=cosx的根。

根据数学知识，27-18x+2x2=cosx有2个根(如图1所示)，GlobalOptimizationSolution搜索出了2个根：x1=1.936 571 998 300 551 6;x2=7.158 983 280 758 961。

通过图1可知，GlobalOptimizationSolution搜索出了2个根，说明GlobalOptimizationSolution的全局搜索能力较佳。

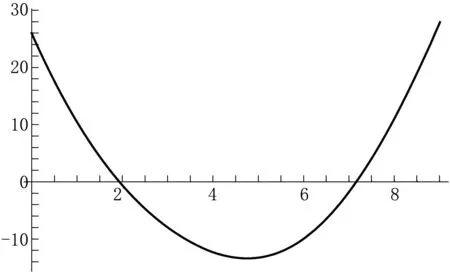
图1　27-27-18x+2x2=cosx的图像

3.2局部搜索

将GlobalOptimizationSolution搜索出的局部根同文献[7]中FAC算法搜索出的局部根进行比较。

算例3：求解(x-1)2sin2x+(x-1)3cos3x+5(x2-1)=0在区间[-5,5]内的根。

通过表2可以看出，结果保留小数点后6位，GlobalOptimizationSolution搜索出的局部根与精确解相等，而FAC方法最大绝对误差为0.000 120，最大相对误差为0.000 120。GlobalOptimizationSolution比FAC方法要精确。

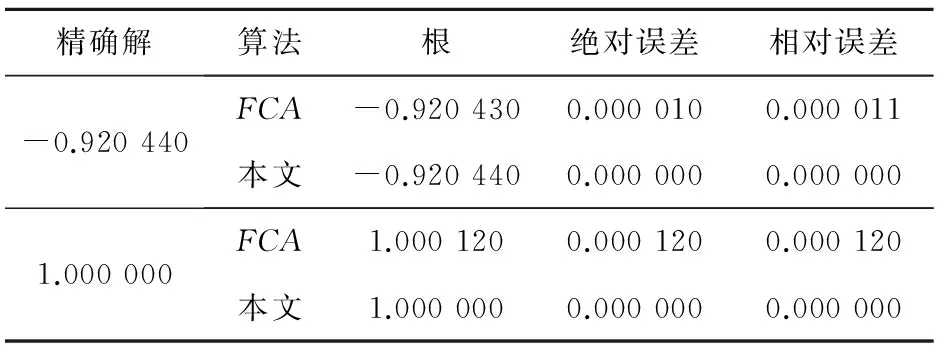
表2　本文方法和FAC法的对比

算例4：求解cos(x-1)-sin2x=0在区间[-3,3]内的根。

通过表3可以看出，结果保留小数点后6位，GlobalOptimizationSolution搜索出的局部根与精确解相比，最大绝对误差为0.000 001，最大相对误差为0.000 002，而FAC方法最大绝对误差为0.000 100，最大相对误差为0.000 046。GlobalOptimi-zationSolution比FAC方法要精确。

3.3计算时间

算例5：分别求解

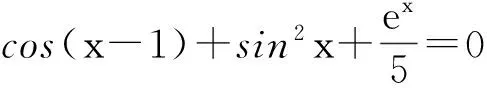
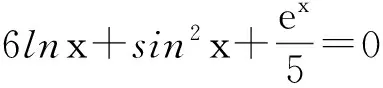
在区间[-3,3]内的根。

表3　本文方法和FAC法的对比

利用文献7中FAC算法、SPSO算法进行计算，与Global Optimization Solution搜索出局部根所花时间进行对比，结果见表4。

表4　本文方法和FAC法、SPSO法的对比

由表4可以看出，Global Optimization Solution的最大耗时为55 ms，FAC法、SPSO法最大耗时分别为398 ms、452 ms。Global Optimization Solution耗时仅为FAC法、SPSO法的13.8%、12.2%；Global Optimization Solution的平均最大耗时为29 ms，FAC法、SPSO法最大耗时分别为224 ms、275.6 ms。Global Optimization Solution的平均耗时仅为FAC法、SPSO法的12.9%、10.5%；Global Optimization Solution的计算成功率为100%，FAC法的计算成功率为100%，但SPSO法的计算成功率在47%～75%。说明Global Optimization Solution是一种计算成功率高，耗时极短的计算方法。

5　结语

Global Optimization Solution充分发挥粒子群算法的全局搜索性能和拟牛顿法的局部搜索性能，进而将超越方程转化为了纯粹的函数优化问题，优点可总结如下：1)Global Optimization Solution全局搜索能力强；2)Global Optimization Solution局部搜索能力强，计算精度高；3)Global Optimization Solution计算耗时短。

[1] Bianchini M,Fanelli S,Gori M.Optimal Algorithms for Well-Conditioned Nonlinear Systems of Equations[J].IEEE Transactions on Computers,2001,50(7):689-698.

[2] 陈子仪,康立山,胡欣.遗传算法在方程求根中的应用[J].Wuhan University Journal of Natural Sciences,1998(5):577-580.

[3] Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C]// Micro Machine and Human Science,1995.MHS '95.,Proceedings of the Sixth International Symposium on.IEEE,1995:39-43.

[4] 刘华蓥.粒子群优化算法的改进研究及在石油工程中的应用[D].大庆：东北石油大学,2012.

[5] 田明俊,周晶.岩土工程参数反演的一种新方法[J].岩石力学与工程学报,2005,24(9):1492-1496.

[6] Jing K E,Qian J X,Qiao Y Z.A modified particle swarm optimization algorithm[J].Journal of Circuits & Systems,2003,26(2):151-155.

[7] 郭改文,黄卡玛.森林竞争算法及在超越方程求解中的应用[J].四川大学学报:工程科学版,2008(6)：127-132.

The Global Optimization Method to Transcendental Equation

XIA Lyu-yu

(TonglingPolytechnic，TonglingAnhui244000，China)

The existing PSO (particle swarm optimization) algorithm has many problems in solving the transcendental equation，such as poor local search ability，post-convergence slower，which causes that PSO algorithm can not get more precise transcendental equation roots.In this article，based on particle swarm optimization algorithm，and adding quasi-Newton algorithm with better local search ability and faster post-convergence，the particle swarm algorithm and quasi-Newton method have been automatically selected and given full performance in local search ability abut this two algorithms.Thus the transcendental equation has been transformed into purely function optimization problem.Based on this method，a solution experiment has been made，and the results show that this method has the very high convergence speed and solution accuracy.

particle swarm optimization；global optimization；quasi-Newton method；transcendental equation

10.3969/j.issn.1009-8984.2016.03.028

2016-05-23

夏绿玉(1983-)，女(汉)，安徽铜陵，硕士，讲师

主要研究概率论与数理统计。

O241.7

A

1009-8984(2016)03-0125-04