经验模态分解的端点问题数值处理方法研究

刘玫星

（湖南邮电职业技术学院经济管理系，湖南长沙410015）

经验模态分解的端点问题数值处理方法研究

刘玫星

（湖南邮电职业技术学院经济管理系，湖南长沙410015）

经验模态分解（EMD）是由Huang等发展的一种新的数据分析方法，但在利用样条插值获得上下包络过程中存在着棘手的端点问题。文章在该问题已有解决方法的基础上，提出了基于极值点单调性一致的EMD端点问题处理方法。根据信号的极值序列查找与数据末端极值的差值和同时具备最小、单调性一致且在单调性内的点数相等三个条件的极值序列，进而构造方程组进行极值预测。通过与其他两种方法的对比验证，证明了提出的方法可以有效抑制端点效应。

EMD端点问题；极值点；单调性一致

1998年，Huang等人在瞬时频率的研究中，提出了希尔伯特黄变换方法，即：HHT；随后对该方法进行了改进，使其分解精度提高；接着对相关的准则进行了完善，给出了一种高尺度分辨率的改进方法。该方法根据信号本身具有的特征时间尺度，第一次提出了本征模态函数（tmf）概念以及将信号分解为固有模态的方法，即：EMD方法［1］。随着研究的深入，EMD方法被运用到越来越多的领域中，EMD方法分解质量也就受到广泛的关注；EMD方法分解是用上下极值点的三次样条插补拟合均值来获得分解信号，但是采用三次样条插补方法存在特殊的端点效应，严重的会影响到信号分解的层数和端部信号的污染。由此，陈忠、郑时雄提出了通过在其两端添加极值点的方法来抑制端点效应，该方法利用端点处三分之一数据时间间隔均值作为时间轴上的延伸和两端点幅值或全局统计平均幅值作为附加极值，由于附加极值预测采用的是两端点幅值或全局统计平均幅值，因此不能很好的体现附加极值的预测性［2］；刘慧婷等人采用了多项式拟合算法来处理EMD端点效应，提出了附加极值预测方法［3］；还有一些学者利用径向基函数神经网络预测附加极值的方法［4］［5］［6］［7］，在信号的两端分别预测下一个极大值和极小值，再进行三次样条曲线插补，该方法预测精确，但时间运行太久；毛博，高斐等人用分段幂函数插值法代替原EMD方法算法中的三次样条插值法［8］，该方法虽然从源头解决了采用三次样条插值法产生的端点效应，但其精度较差，且还产生了一些新的问题。上述研究方法中，主要存在时间和精度不能同时达到最优的问题，因此本文基于附加极值的思想提出了使时间和精度能同时达到最优的单调性一致的EMD端点附加极值预测方法，简称单调性算法。

1　EMD端点问题的极值点单调性处理方法研究

EMD方法［9］从原理上讲是对一个信号进行平稳化处理，其结果是将信号中不同尺度的波动或趋势逐级分解，产生一系列具有不同特征尺度的数据序列，每个序列成为1个固有模态函数（imf）。但是在分解过程中会有端点效应的产生，针对端点效应常见采用的有端点极值法、用全局统计平均幅值作为端点的附加极值法［2］、多项式拟合算法、对称延拓算法和镜像延拓基算法。在上述算法中对称延拓和镜像延拓是基于局部近似预测，而端点极值法、全局统计平均幅值作为端点的附加极值法和多项式拟合算法都是基于三次样条插补算法。

信号可以分为周期信号和非周期信号，而非周期信号可以看作是周期无限大的周期信号，可以近似的认为信号具有周期性，因此提出了对称延拓算法和镜像延拓基算法。而对称延拓算法和镜像延拓基算法只是基本的运用信号具有周期性、计算简单和时间短等特点，但并没有去判断和识别出与末端局部信号最近似的局部信号进行对称或镜像，所以计算精度很低，因此本文提出基于信号极值点之间的相关性（单调性）来寻找最近似的局部信号，然后采用极值点的多项式拟合求解末端的下一个极大和极小值，具体方法如下：

1）提取信号x（t）的极大值pmax与极小值pmin，右端最近的一个极大pmax（end）与极小值pmin（end）；将对应的极大值与极小值之差的绝对值相加得误差集，即：并将误差集从小到大排列；

2）求右端点最近的极大值与极小值的左边的单调性情况，即：，与所求误差集中的每一点（i）的左边的单调性进行比较，如果单调性与数量的个数（m1）一样，则保留，否则删除；

3）计算误差集中的点（i）右边第一个极值是否与左边单调性一致的情况，即：，比较1-4四种情况的出现频率，选择出现频率较高者，相差不大（＜3）认为同等；

4）选择单调性中点的个数（m1）与误差集中的点的个数（m2）较小的数（m），构造方程或方程组，即：

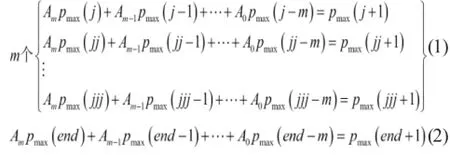
将方程（1），即：AX=B求解出的系数A代入方程（2）中，解出pmax（end+1），其坐标由误差集中最小误差点坐标和后一个坐标差加上端点pmax（end）坐标。右端极小值可以使用同样的方法求得；将信号倒置后，采用同样的方法可以得到左端极大值与极小值。

由于该方法是基于极值误差和的方法寻找近似点得出的，部分筛选条件将过于严格，因此在数据很少时可能导致无解，这时将进行如下处理：在步骤a提取出极大值pmax与极小值pmin时，右端的第一个极大pmax（end）与第一个极小值pmin（end）分别与剩余的极大值与极小值相减得到差值，两差值的绝对值相加就得了误差集，如下式并从小到大排列，再按照b，c，d步骤进行求解，单调性算法流程如图1。

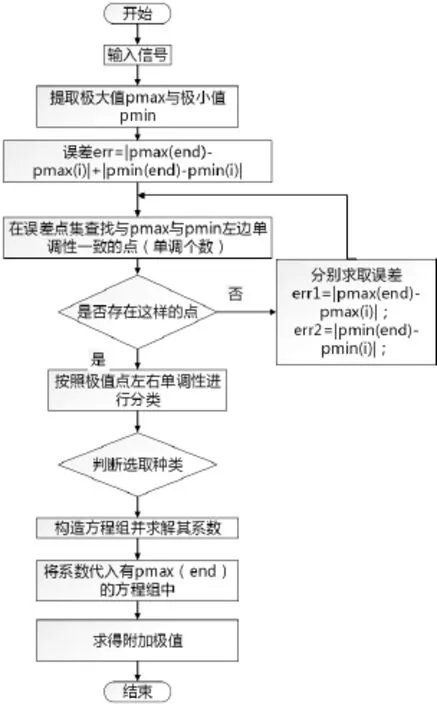
图1　单调性算法流程图

2　方法论证

2.1三种方法的端点极值的预测比较

在经验模态分解过程中常用来处理端点效应的方法是三次样条插补，其实质是对信号两端的极大值和极小值预测，其预测的极值与真实值越接近，其误差就越小［10］。所以通过比较预测两端的极大值和极小值，可以得出端点效应强与弱，因此下面将通过端点极值法、径向神经网络RBF和本文提出的单调一致性方法对信号两端的极值进行对比分析，并与真实值进行比较。

设信号x（t）由调幅信号x1（t）和正弦信号x2（t）合成，即：

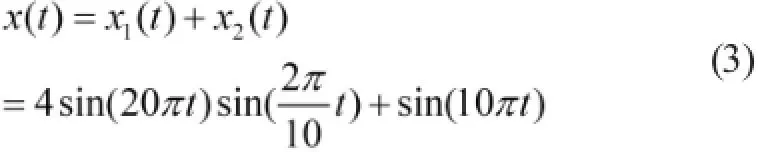
其信号如图2所示。

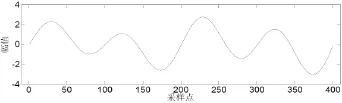
图2　信号x（t）图

图3　三种方法求得预测极值和实际极值的包络线图

如图3是分别采用上述三种方法得到包络线图和实际包络线图。其中“.”代表实际值包络线点；“*”点是由端点极值法得到极值再采用三次样条插补得到点，从图4中可以看出左端极大值和右端极小值所拟合得到的点较为靠近真实的值，而左端极小值和右端极大值拟合所得出来的点离真实值较远，其端点效应较为强烈；“+”点指由径向神经网络RBF三次样条插补曲线，其左右两端的极小值所预测值的插值点离实际点较小的偏差，而两端的极大值所预测值的插值点与真实结果十分靠近，其端点效应较弱；“-”是由本文提出的单调一致性算法得出的结果，其左右两端的极大值所预测值的插值点离实际点有较小的偏差，而两端的极小值所预测值的插值点与真实结果基本一致，因此所带来的端点效应较弱。从整体上，单调性预测极值和径向神经网预测极值都比以数据端点作为极值点好，且单调性算法预测的极值与径向神经网络预测的极值具有相等的精度。

2.2实验验证

发生机械故障时，故障信息往往以调制形式存在于振动和噪声中，调制信号反映了故障的特征信息［11］［12］。下面仿真常见的机械振动信号，信号是由基频为7.5Hz，调制频率15Hz，30Hz的调频调幅信号和频率为120Hz正弦信号叠加。以MATLAB14a为仿真软件，win8系统，处理器为Intel（R）Core（TM）i5-2400，表达式为［13］：

图4三种方法分解的结果比较图

图4是利用以数据端点作为极值点、神经网络延拓、单调性三种算法对该振动信号分解后的结果（图中纵坐标为幅值；横坐标为采样点数）。从图4（a）的分解结果可知，对于该仿真的振动信号，采用直接以数据端点作为极值点，虽然很好地抑制了分解得到的imf的端部特征，但是它实质是强制扭曲了信号的端部特征，因此严重污染了信号。从图4（b）的分解结果可知，神经网络延RBF拓算法较好地抑制了端点效应，还能很好分解出x1（t）与x2（t），但由于在每次循环中要利用该方法对原始数据序列的两端进行数据延拓，每次若延拓到下一个极值点，循环次数为从信号的末点到下一个极值点中间所有的点个数。但采样率过高时则循环次数增加，运算时间也会进一步增加，由表1可知，循环次数太多造成了运算速度太慢。从图4（c）的分解结果可知，单调性方法对该振动信号的分析结果十分理想，不但能抑制端点效应，还能将表达式x1（t）与x2（t）很好分解出来，而且时间很短，由表1可知。

表1　三种算法运行时间

由端点数据为附加极值、神经网络RBF、单调性三种方法来预测附加极值的比较中，能够得出数据端点为附加极值点的方法抑制端点效应非常有效果，但是在数据量少时，其附加极值的误差带来了分解层数的增加，产生不存在的im f分量；神经网络延拓算法，抑制端点效应结果很好，没有产生不存在的imf分量，但缺点却十分的明显，运算速度太慢了；单调性方法能抑制端点效应，没有产生不存在的imf分量，运算时间小于神经网络RBF的百分之一，其分解的精度和神经网络相差甚小。所以不论从理论分析还是实验分析中可以看出该算法是一种能较好处理端点效应的方法。

3　结论

本文基于信号周期性的特点，提出单调性一致算法，该方法能减弱经验模态分解时所产生的端点效应，并保证了端点局部信号完整性，保证了端点预测值与端点局部密切相关，由此保证了预测值的可靠性和高精度性。单调性算法本质属于对称延拓算法和镜像算法的改进，所以单调性算法同时具有计算简单和计算时间短的特性。

［1］范虹.非平稳信号特征提取方法及其应用［M］.北京：科学出版社，2013.125-126.

［2］陈忠，郑时雄.EMD信号分析方法边缘效应的分析［J］.数据采集与处理，2003（3）：114-118.

［3］刘慧婷，张旻，程家兴.基于多项式拟合算法的EMD端点问题的处理［J］.计算机工程与应用，2004（16）：84-86.

［4］乔新勇，赵秀玉，刘春华.一种抑制EMD端点效应的改进方法［J］.软件，2012（8）：72-74.

［5］瞿威廉，程磊.应用径向基函数神经网络处理EMD方法中的边界问题［J］.华中科技大学学报（城市科学版），2006（4）：1-4.

［6］韩建平，钱炯，董小军.采用镜像延拓和RBF神经网络处理EMD中端点效应［J］.振动.测试与诊断，2010（4）：414-417，474.

［7］郭云喜，张洁.采用RBF和BP神经网络处理EMD分解过程中端点效应［J］.机械，2012（8）：18-21.

［8］毛博，高斐，孟军.一种基于分段幂函数插值法的经验模态分解方法及其应用研究［J］.中国测试，2013（2）：125-128.

［9］Huang NE eta1.The empiricalmode decomposition and the HilbertSpectrum fornonlinearand non-stationary time seriesanalysis［J］.ProcRSoc Lond A.，1998（1971）：903-995.

［10］程军圣，于德介，杨宇.机械故障诊断的Hilbert-Huang变换方法［M］.北京：科学出版社，2006.

［11］Jonathan Derota，etal.Correlation between long-term marine temperature time series from theeastern andwestern English Channel：Scaling analysisusingempiricalmode decomposition［J］.ComptesRendusGeoscience，2016（5）：343-349.

［12］ShutangYou，etal.Oscillationmode identification based on wide-area ambientmeasurementsusingmultivariate empiricalmode decomposition［J］.Electric PowerSystem Research，2016（134）：158-166.

［13］顾小兴，金涛，郭艳威.改进EMD端点效应电力系统HHT谐波检测研究［J］.中国测试，2015（3）：99-102，107.

Numericalprocessingmethod of endpoint issueof EMD

LIU Mei-xing
（DepartmentofEconomic Management，Hunan Postand Telecommunication College，Changsha，Hunan，China410015）

The EmpiricalMode Decomposition（EMD）is a newmethod for data analysis developed by Huang，etc.But there is a troublesome endpoint issue during the course of obtaining two envelops of the data with spline interpolation.A new endpoint issue processingmethod based on samemonotonicity of extreme points is proposed on the basis of existing algorithms.The difference values between theextremumsof data end are looked up according to theextremum sequencewhich satisfies the conditions simultaneously such as minimum value，same monotonicity and equal point count in the monotonicity zone.Then the extremums are predicted with constructed equation set.It is verified that the proposed method can restrain endpoint effectavailably by the comparison experiments with theother twomethods.

endpoint issue of EMD；extreme point；samemonotonicity

10.3969/j.issn.2095-7661.2016.03.022】

TN911.7

A

2095-7661（2016）03-0076-04

2016-06-25

刘玫星（1967-），女，湖南新化人，湖南邮电职业技术学院副教授，本科，研究方向：数据处理、智能算法。