斜拉桥易损性分析的合理地震动强度指标评估

钟　剑， 庞于涛， 袁万城

(同济大学 土木工程防灾国家重点实验室，上海 200092)



斜拉桥易损性分析的合理地震动强度指标评估

钟剑， 庞于涛， 袁万城

(同济大学 土木工程防灾国家重点实验室，上海 200092)

以迫龙沟特大跨斜拉作为工程背景，用OpenSEES开源程序建立考虑多重非线性效应的有限元模型，从太平洋地震工程研究中心(PEER)中选择80组地震波纵向和横向输入.通过高效性、实用性、熟练性、充分性以及灾害可计算性等5个指标，详细讨论并比较了峰值加速度(PGA)、峰值速度(PGV)、和结构一阶周期、0.2 s以及1.0 s对应的加速度反应谱数值(Sa-T1、Sa-02、Sa-10)作为地震动强度指标的优缺点.结果表明，PGA具有最好的充分性和实用性，在高效性和熟练性上也表现得很好，因此是最为合理的斜拉桥地震动强度指标.

地震易损性; 概率需求地震模型; 斜拉桥; 地震动强度指标; OpenSEES

1　背景

作为目前抗震理论研究的热点问题，美国太平洋地震工程研究中心(PEER)于2005年提出新一代基于性能的地震工程研究框架[1]，其中地震易损性分析为该框架的重要环节和热点之一.

易损性曲线是在特定的地震动强度水平下，构件响应(D)达到或超越某一损伤水平(C)的条件概率，概率需求地震模型(PSDM)是计算得到易损性曲线的第一步.结构易损性曲线的计算见式(1).因此，地震动强度指标(intensity measure,IM，以IM表示)选择的好与坏是影响易损性曲线准确与否的一个至关重要的因素.

(1)

式中:Fr为地震损伤概率;IM为地震动强度指标;Φ(·)为标准正态分布累积密度函数;SD和SC分别为响应与能力的均值;βD|IM为地震响应的标准差.

由此可见IM的选择好与坏对易损性曲线的计算结果正确与否至关重要.

很多学者都致力于IM选择的研究.美国应用技术委员会(ATC)[2]早在1985年ATC-13的时候用修正的麦加利地震烈度作为IM，而最近ATC-63/FEMA P695[3]改为使用结构基本周期对应的加速度反应谱值Sa(T1)最为合理的IM.而风险评估软件包HAZUS-MH[4]所选择的IM为峰值加速度(PGA，以PGA表示)，峰值速度(PGV以PGV表示)和1.0 s周期对应的加速度反应谱Sa-1.0.Luco等[5]也认为跟结构特性有关联的Sa-T1最为合理的IM.考虑结构第二阶周期和非线性的有关的IM也被学者发现并测试，认为是比较合理的IM[5].Bazzurro等[6]以及Shome等[7]建议用向量IM，包含Sa-T1和Sa-T1/Sa-T2，其中T2为结构的第二阶周期.Baker等[8]同样提出了向量作为合理的IM，该向量元素为Sa-T1以及地震震级(M)，震中距(R)取其一.Padgett等[9]，Shafieezadeh等[10]对一组考虑几何参数(比如墩高，跨度)变换的桥梁进行研究，结果表明PGA是比较合理的IM选择.Mackie等[11]用典型的加州桥梁为模型研究了24个IM来模拟PSDM的优缺点，研究表明，Sa(T1)以及T1对应的位移谱Sd-T1是比较理想的IM，可以减少PSDM的方差.

以上的研究绝大多数都是基于跨度较小的普通梁桥，其周期较短，高阶阵型较少.但是大跨度斜拉桥具有周期长，高阶阵型对结构响应影响大等特点，因此，合理的地震动强度指标很有可能不同于普通梁桥.故本文展开斜拉桥概率地震需求模型的合理地震动强度指标的研究，为大跨度斜拉桥的地震易损性曲线以及基于性能的斜拉桥概率性抗震设计做理论支撑.

2　方法

一个理想的IM应该具有怎么样的特性？

Giovenale等[12]指出充分性(sufficiency)，高效性(efficiency)以及灾害可计算性(hazard computability)是一个好的IM应该具有的特征.此外实用性(practicality)[5]以及熟练性(proficiency)[9]也应该被考虑.Shafieezadeh[10]对每一个特性做了细致的讨论.

假设结构的地震动响应SD服从幂函数分布：

(2)

式中，a和b为幂函数的拟合系数.

(3)

(1) 高效性：指在生成PSDM模型的过程中，变异系数较低，简单地说就是式(1)中的标准差βD|IM较低.

(2) 实用性：指响应依赖IM程度的大小，通常通过拟合系数b来表示.当b很小时，说明对数线性拟合得到直线斜率较小，响应和IM的关联性就很小，因此不是实用的IM.

(3) 熟练性：结合高效性和实用性的一个复合指标，定义熟练性(为式(4),可以转化为式(5)).

(4)

(5)

式中，ζ为反应熟练性的一个参数，ζ越小，表明随机性越小，因此是更合理的IM.

(4) 充分性：该特性是为进行PSDM全概率理论的基础.充分性指IM和地震动的特性(比如震级M，震中距R)无关.这样在计算全概率结构失效概率时，不用在依据其他的条件概率.当IM不充分时，结构易损性需要表示为Fr[SD≥SC|IM,M,R].充分性以数理统计中假设检验结果的p值来经行验证，p值通过对基于IM的地震需求参数(EDPs)的残余值与地震动特性(震级M，震源距离R)进行回归分析计算得到.越小的p值表明越高的统计显著性，也是拒绝IM的原因.

(5) 灾害可计算性：是指通过IM建立的易损性曲线可以和地震危险性曲线结合起来，计算构件的全概率灾害：

(6)

式中:λ(D)为超越某一特定性能水平的概率;ν(IM)为地震灾害曲线.

3　工程实例

迫龙沟大桥是位于中国西藏自治区林芝地区波密县境内的一座公路斜拉桥，是西藏自治区主跨最长的斜拉桥.大桥全长742 m，为双塔双索面混合梁斜拉桥，本桥为主跨430 m的混凝土梁加组合梁的混合梁斜拉桥，其中主梁中跨采用组合梁，边跨采用混凝土梁.跨径组成为：156 m+430 m+156 m，桥型总体布置图见图1.图中A1和A2表示桥台1和桥台2，P1和P2表示桥塔1和桥塔2.

主桥纵向为漂浮体系，加劲梁与塔、墩之间均设置竖向支座，纵向滑动；主塔与主梁之间设置横向抗风支座，限制主梁的横向位移；辅助墩、桥台设置纵向滑动球型钢支座.

图1　迫龙沟桥总体布置示意图(单位：m)

3.1数值模拟

由于本文所选算例的塔柱为钢筋混凝土结构，本文利用OPNESEES的弹塑性纤维单元nonlinearBeamColumn模拟，该单元将钢筋和混凝土离散为纤维，假设纤维之间完全粘结，且满足平截面假定.

a Kent-Scott-Park模型

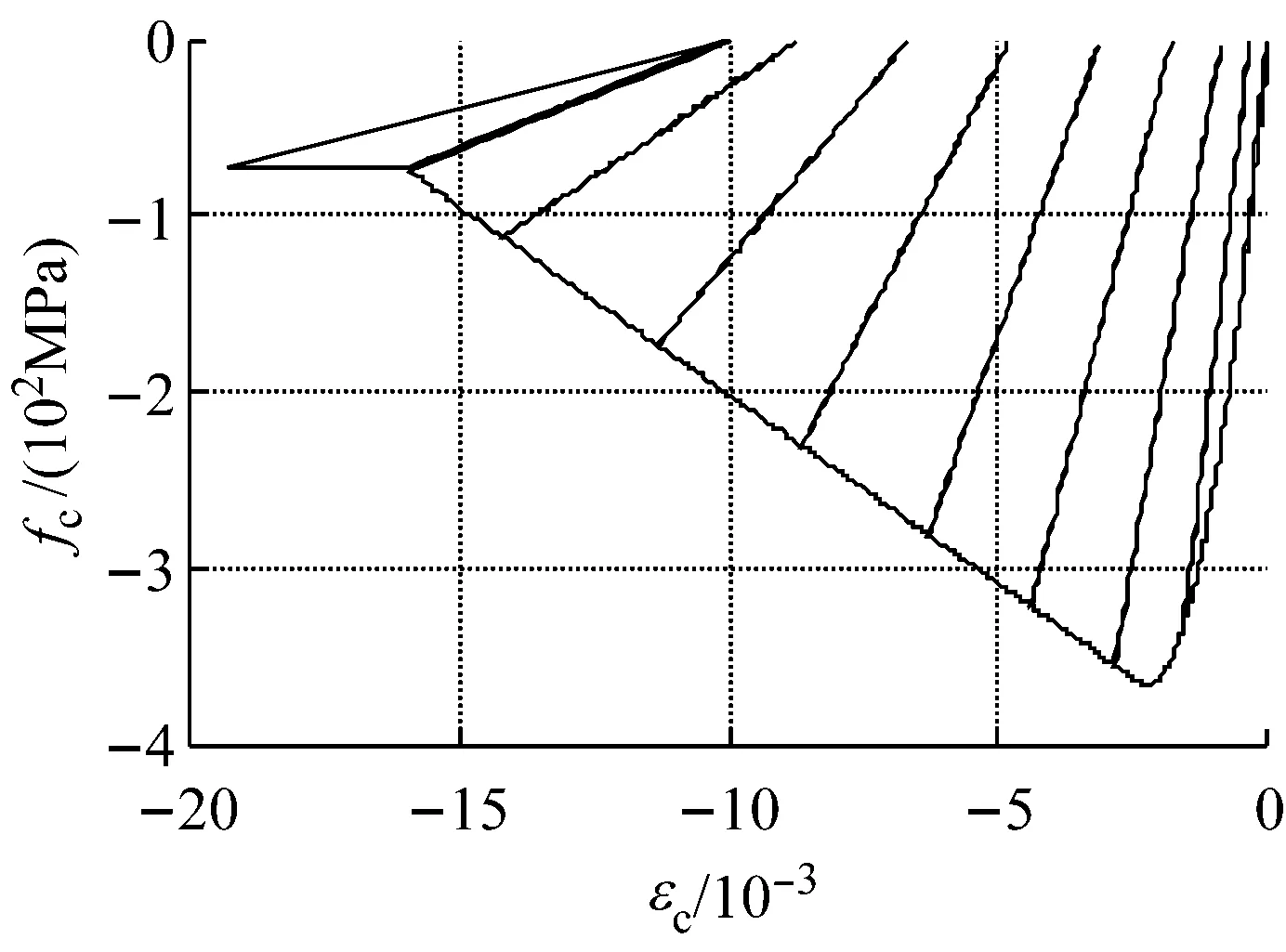
b 核心混凝土滞回曲线

桥台处和桥塔处布置纵向滑动、横向设置剪力销的球型钢支座，μ为滑动摩擦系数，FN为支座承受的压力，图中Δy为临界位移.按规范[13]取μ=0.02，Δy=0.002.对斜拉桥做恒载分析可以得到桥台处和桥塔处的支座反力分别为5 000 kN和15 000 kN；对应的初始刚度分别为5.0×104kN·m-1和1.5×105kN·m-1.

假定拉索在地震过程中处于弹性状态，用truss单元进行模拟，同时考虑斜拉索的垂度效应和拉索的预加应力.主塔的群桩基础的刚度用六弹簧模拟.

分析结果表明：与恒载作用下结构关键截面的响应相比，地震作用下主梁和拉索的地震反应均不起控制作用；其应力水平相对自身的材料能力水平较低，因而在地震中是不易损伤的构件，因此本文假设主梁处于弹性状态.

斜拉桥的计算模型及前四阶周期见表1.

3.2地震波选取

本文选用Shafieezadeh[10]在其文章中使用的地震波，为80条从太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center，PEER)(http://peer.berkeley.edu/smcat)强震地震库里选取的地震波[14]，从PEER里选择的是一组震级和震中距分布均匀的地震波，这些波震级从5.8到6.9，震中距从10～60 km.这些地震波的PGA，震级和震中距的分布图见图3a；纵向加速度反应谱见图3b，其中粗线条为80条反应谱的均值.

表1　计算模型基本动力特性

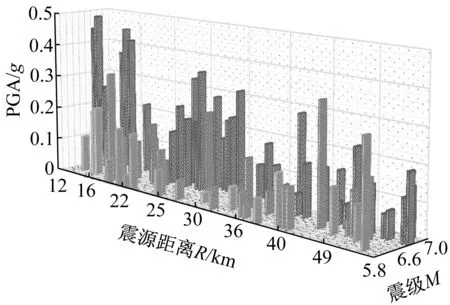
a 震级和震中距分布图

b 纵向加速度反应谱图

3.3合理的地震动强度指标比较

结合文献中常用的地震动强度指标，本文选取峰值加速度(PGA)，峰值速度(PGV)以及第一阶周期T1，0.2 s和1.0 s周期对应的加速度反应谱Sa-T1，Sa-02，Sa-10等5个地震动强度指标.由于Sa-T1是基于结构的指标，而大多数的地震灾害曲线都是针对跟结构无关的参数，比如PGA，PGV等，因此无法进行结构的灾害计算，故本文将仅比较PGA，PGV，Sa-02，Sa-10四个最常用的指标.

本章选用桥塔底部纵向横向弯矩屈服曲率(μφx和μφy)，桥台后填土被动土压力导致的桥台位移(δn)，桥台后填土主动土压力导致的桥台位移(δp)，桥台横向位移(δt)，支座纵向位移(δb)，主梁和桥台的相对位移(δd)等7个工程需求参数(EDPs).

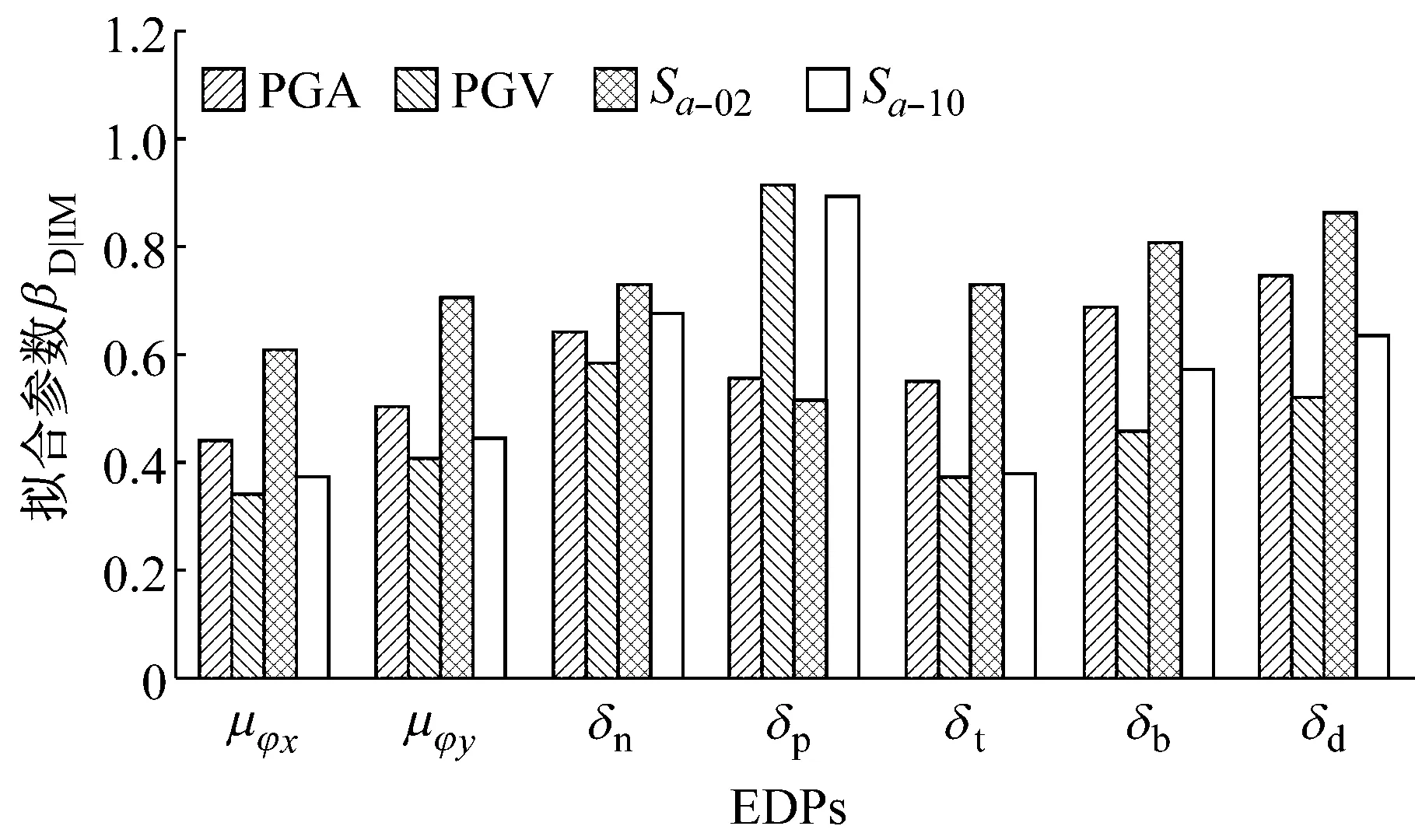
根据已知的加速度时程曲线，通过Matlab程序编程计算得到80条地震波的PGA，PGV，Sa-T1，Sa-02，Sa-10.对上述的4个EDPs参数，用不同IMs进行拟合，μφx拟合的结果如图4所示，其他具体的参数见表2，表中b的最大值以及ζ和βD|IM最小值标注为黑体，方便后续分析合理的IMs时使用.

(1) 高效性和实用性

指在生成PSDM模型的过程中，变异系数较低，简单地说就是标准差βD|IM较低.其具体的参数见表2，表中βD|IM最小值标注为黑体，从图5a可以进一步看出，除了对于δp这个EDP之外，其他6个EDPs的最小标准差βD|IM对于的IM均为PGV，因此仅从高效性的角度出发，PGV为最优的IM，基本排序大致为PGV>Sa-10≥PGA>Sa-02.

表2　不同IM的拟合参数

实用性指响应依赖IM程度的大小，通常通过拟合系数b来表示.当b很小时，说明响应和IM的关联性就很小，因此不是实用的IM.从表2(b最大值标注为黑体)和图5b中可以看出，针对不同的EDPs，PGA作为IM时所拟合出的b值最大.因此，从实用性角度出发，PGA为最合适的EDP.大致排序为PGA>Sa-02>Sa-10>PGA.

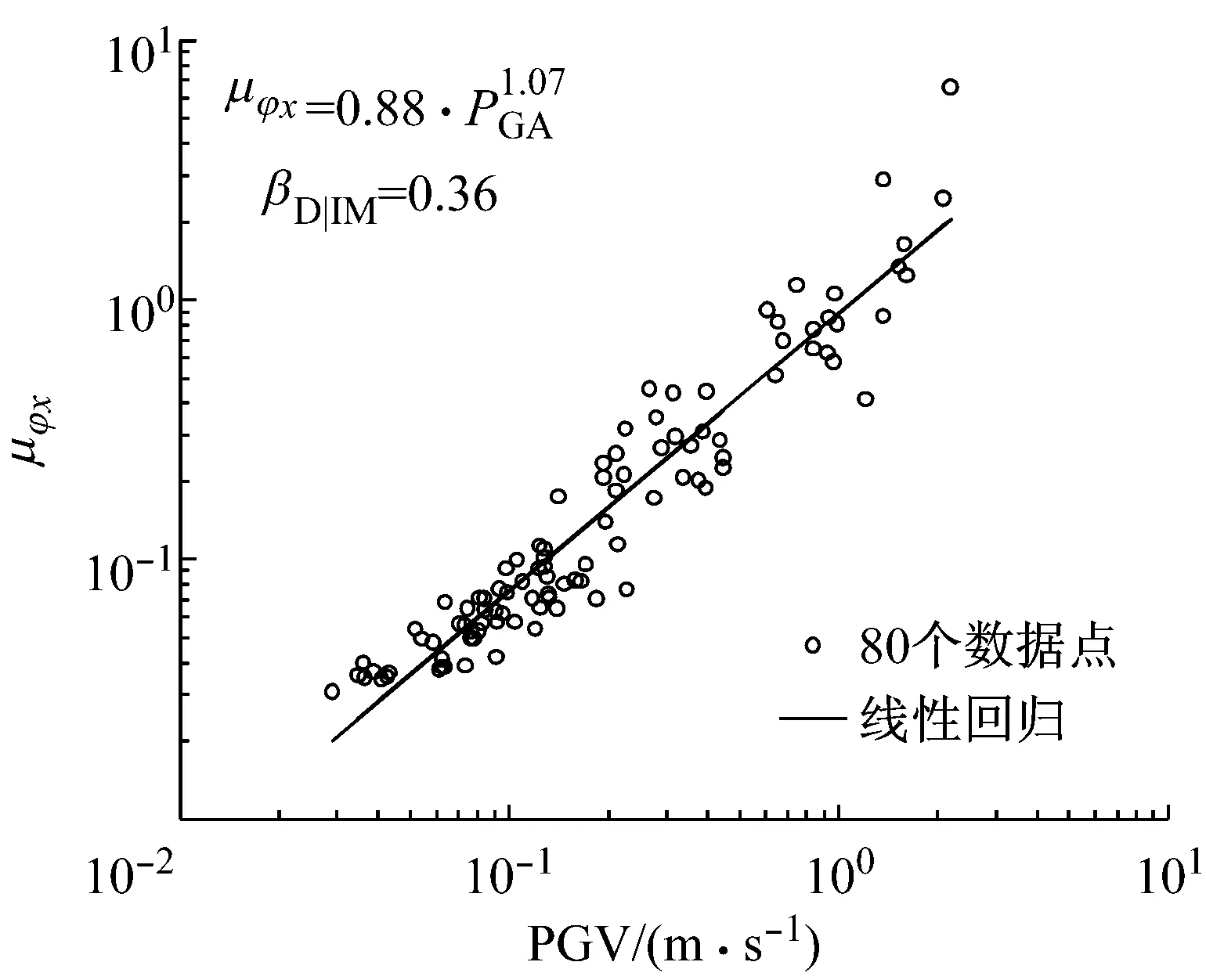
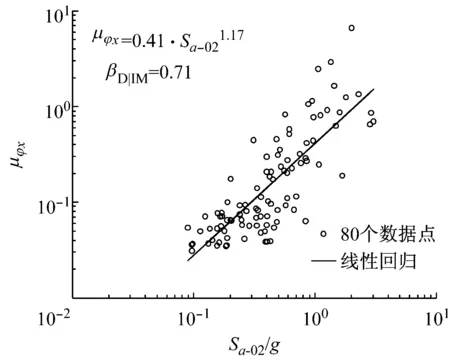
图4　μφx的PSDM曲线拟合

(2) 熟练性

是结合高效性和实用性的一个复合指标，ζ越小，表明随机性越小，因此是更合理的IM.从图5c中可以得出，6个EDPs的最小ζ所对应的EDP为PGV，因此仅从熟练性的角度出发，PGV为最优的IM，排序大致为PGV>Sa-10≥PGA>Sa-02.

a 高效性

b 实用性

c 熟练性

Fig.5Comparison of efficiency, practicality and proficiency between four different IM candidates

(3) 充分性

该特性是为进行PSDA全概率理论的基础.充分性指其和地震动的特性(比如震级M，震中距R以及ε)无关.这样在计算全概率结构失效概率时，不用在依据其他的条件概率.当IM不充分时，全概率需要表示为λ(D)=[D≥d|IM,M,R].充分性具体可以通过p值来计算，越小的p值表明越高的统计显著性，也是拒绝IM的原因.p值通过对基于IM的EDPs的残余值与地震动特性(震级M，震源距离R)进行回归分析计算得到.

(7)

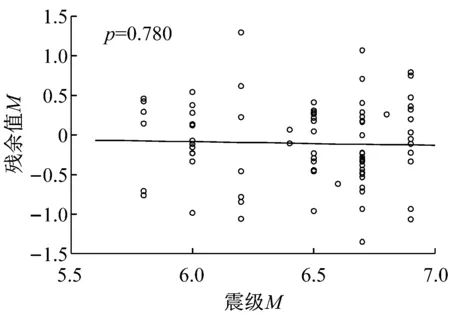
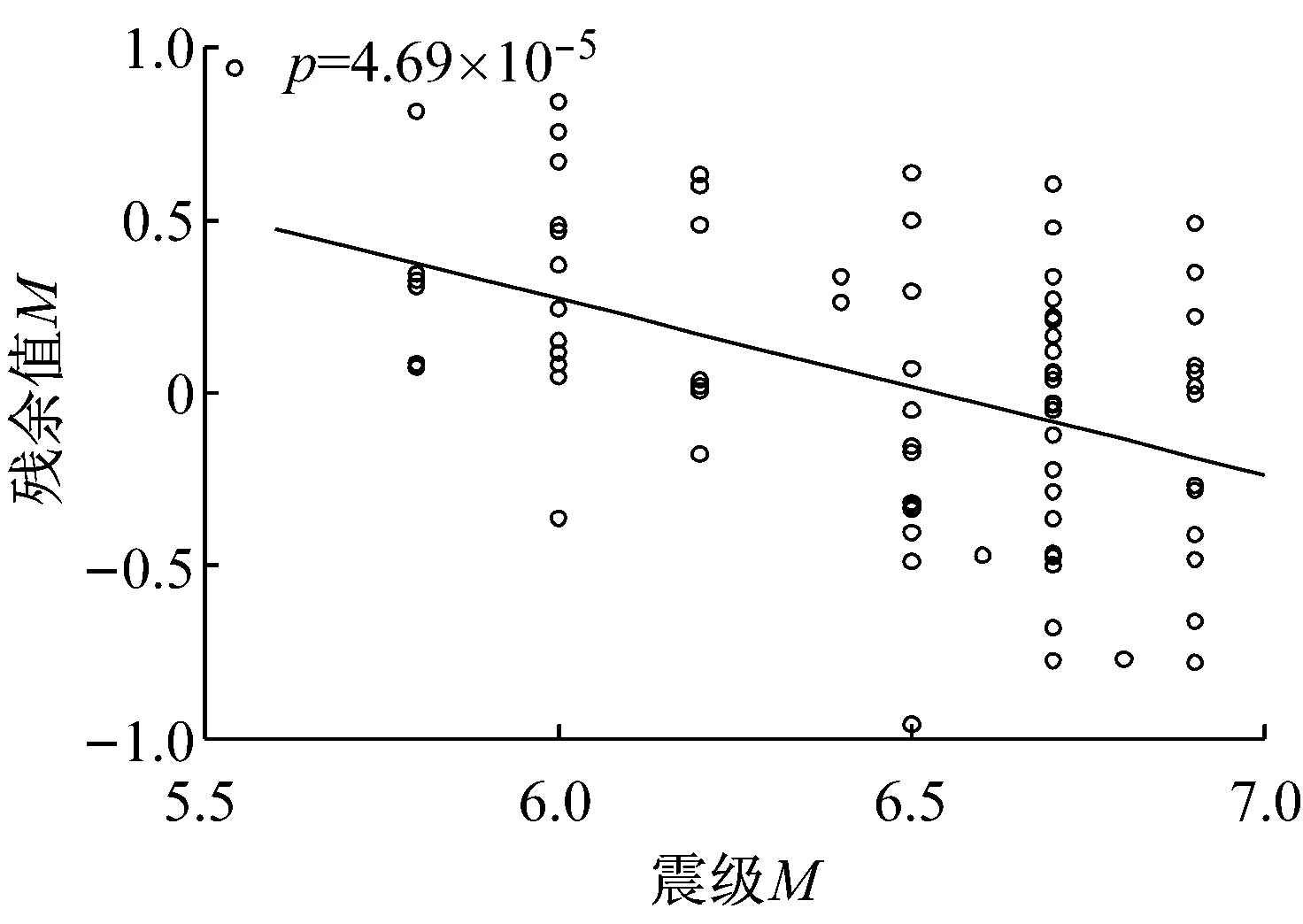
Shafieezadeh[10]给出了前80条实测地震波的震级M和震中距R，通过计算不同IM下的各个工程需求参数EDPs的残余值(真实值与拟合值的差值)，得到相对于地震特性的两个参数震级(M)和震中距(R)的p值，图6以μφx为例演示了震中距p值的计算方法，详细的结果见图7和表3.

a PGA

b PGV

a Sa-02

b Sa-10

a 相对于震级M的p值

越小的p值表明越高的统计显著性，也是拒绝IM的原因，本文中选择p值为0.1为拒绝的阀值，小于等于0.1的值在表3用黑体标出.

可以看出，相对与M的p值，当选择PGA为IM时，表格中前5个EDPs的p值均较大，后两个EDPs，即支座位移以及主梁与桥台的相对位移的p值小于0.1.当PGV为IM时，主塔底部弯曲曲率(纵向和横向)以及桥台的被动位移和横向位移等4个EDPs的p值均小于或等于0.1，对于支座位移以及主梁与桥台的相对位移，其p值较大.当Sa-02或者Sa-10为IM时，与PGA一样，都是δb和δd的p值小于0.1.

表3　不同地震需求参数4个地震强度指标的p值检验

相对于R的p值，除PGV作为IM时，δn的p值小于0.1，其余均大于0.1.

综合比较PGA，PGV，Sa-02，Sa-10等4个IMs对应的p值，以及综合考虑各个构件的重要性(比如，桥塔的延性曲率显然要比桥台的位移是更为重要的EDP)，4个参数的表现可以排序为PGA>Sa-02=Sa-10>PGV.

因此虽然PGV在高效性和实用性两个指标上比PGA略优，但是考虑充分性指标，PGA要比PGV好很多，综合考虑以上4个IMs，本文的迫龙沟斜拉桥选择PGA为IM是比较合适的.

Shafieezadeh[10]给出了前80条实测地震波的震级M和震中距R，通过计算不同IM下的各个工程需求参数EDPs的残余值(真实值与拟合值的差值)，得到相对于地震特性的两个参数震级(M)和震中距(R)的p值，图6以μφx为例演示了震中距p值的计算方法，详细的结果见图7和表3.

越小的p值表明越高的统计显著性，也是拒绝IM的原因，本文中选择p值为0.1为拒绝的阀值，小于等于0.1的值在表3用黑体标出.

可以看出，相对与M的p值，当选择PGA为IM时，表格中前5个EDPs的p值均较大，后两个EDPs，即支座位移以及主梁与桥台的相对位移的p值小于0.1.当PGV为IM时，主塔底部弯曲曲率(纵向和横向)以及桥台的被动位移和横向位移等4个EDPs的p值均小于或等于0.1，对于支座位移以及主梁与桥台的相对位移，其p值较大.当Sa-02或者Sa-10为IM时，与PGA一样，都是δb和δd的p值小于0.1.

相对于R的p值，除PGV作为IM时，δn的p值小于0.1，其余均大于0.1.

综合比较PGA，PGV，Sa-02，Sa-10等4个IMs对应的p值，以及综合考虑各个构件的重要性(比如，桥塔的延性曲率显然要比桥台的位移是更为重要的EDP)，4个参数的表现可以排序为PGA>Sa-02=Sa-10>PGV.

因此，虽然PGV在高效性和实用性两个指标上比PGA略优，但是考虑充分性指标，PGA要比PGV好很多，综合考虑以上4个IMs，本文的迫龙沟斜拉桥选择PGA为IM是比较合适的.

4　结论

本文以迫龙沟特大跨斜拉作为工程背景，用OPENSEES开源程序建立考虑多重非线性效应的有限元模型，从PEER中选择80条地震波.通过高效性、实用性、熟练性、充分性以及灾害可计算性等5个指标，详细讨论并比较了峰值加速度(PGA)、峰值速度(PGV)、和结构一阶周期、0.2 s以及1.0 s对应的加速度反应谱数值(Sa-T1、Sa-02、Sa-10)作为地震动强度指标的优缺点.

因此虽然PGV在高效性和实用性两个指标上比PGA略优，但是考虑充分性指标，PGA要比PGV好很多，综合考虑以上5个IMs，选择PGA作为斜拉桥IM时是比较合适的.

[1]ATC. FEMA 445, Next-generation performance-based seismic design guidelines-program plan for new and existing buildings [R]. Redwood City：Applied Technology Council, 2006.

[2]ATC. Earthquake damage evaluation data for California [R]. Redwood City: Applied Technology Council, 1985.

[3]ATC. Quantification of building seismic performance factors [R]. Redwood City：Applied Technology Council, 2008.

[4]HAZUS-MH. Multi-hazard loss estimation methodology: earthquake model HAZUS-MH MR5 [R]. Washington D C: Federal Emergency Management Agency, 2011.

[5]Luco N, Cornell C.A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions [J]. Earthquake Spectra, 2007, 23(2): 357.

[6]Bazzurro P, Cornell C A. Seismic hazard analysis of nonlinear structures. I: Methodology [J]. Journal of Structural Engineering, 1994, 120(11): 3320.

[7]Shome N, Probabilistic seismic demand analysis of nonlinear structures [D]. Stanford : Stanford University, 1999.

[8]Baker J W. Vector-valued ground motion intensity measures for probabilistic seismic demand analysis [R]. Stanford: Stanford University, 2006.

[9]Padgett J E, Nielson B G, DesRoches R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios [J]. Earthquake Engineering & Structural Dynamics, 2008, 37(5): 711.

[10]Shafieezadeh A, Ramanathan K, Padgett J E,etal. Fractional order intensity measures for probabilistic seismic demand modeling applied to highway bridges [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(3): 391.

[11]Mackie K. and Stojadinovic B. Probabilistic seismic demand model for California highway bridges [J]. Journal of Bridge Engineering, 2001, 6(6): 468.

[12]Giovenale P, Cornell C A, Esteva L. Comparing the adequacy of alternative ground motion intensity measures for the estimation of structural responses [J]. Earthquake Engineering & Structural Dynamics, 2004, 33(8): 951.

[14]Medina R A, Krawinkler H. Seismic demands for nondeteriorating frame structures and their dependence on ground motions [R]. Stanford: The John A. Blume Earthquake Engineering Center, Stanford University, 2003.

Evaluation of Optimal Intensity Measures in Fragility Analysis of Cable-stayed Bridges

ZHONG Jian, PANG Yutao, YUAN Wancheng

(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

In this study, the finite element model of Polonggou cable-stayed bridge is established using OpenSEES software considering multiple nonlinear effects. 80 pairs of ground motions are chosen from Pacific Earthguake Engineering Research Center(PEER), with the input of longitudinal and transvers direction. The five index: efficiency, practicality, proficiency, sufficiency and hazard computability, are adopted to discuss and compare the advantage and disadvantage of the five IMs, peak ground acceleration(PGA), peak ground velocity(PGV),Sa-T1、Sa-02、Sa-10(acceleration response spectrum at the period of the first mode, 0.2 s and 1.0 s). The results shows that PGA is the best in terms of the index of sufficiency and practicality, and relatively good in terms of the index of efficiency and proficiency. So the PGA is the selected as the best intensity measure(IM) for cable-stayed bridges.

seismic fragility; probabilistic seismic demand model(PSDM); cable-stayed bridges; intensity measure; OpenSEES

2015-08-19

国家自然基金(51478339,51278376,91315301),土木工程防灾国家重点实验室基金项目(SLDRCE14-B-14),江西省科技项目(20151BBG70064).

钟剑(1988—)，男，工学博士，主要研究方向为桥梁抗震与振动.E-mail: china01zhong@126.com

袁万城(1964—)，男，研究员，博士生导师，主要研究方向为桥梁抗震与振动.E-mail: yuan@tongji.edu.cn

TU312.1

A