铝合金构件高强螺栓牙板连接性能试验

蒋首超， 叶中楠， 郭小农

(1. 同济大学，土木工程学院，上海 200092；2. 土木工程防灾国家重点实验室(同济大学)，上海 200092)



铝合金构件高强螺栓牙板连接性能试验

蒋首超1,2， 叶中楠1,2， 郭小农1

(1. 同济大学，土木工程学院，上海 200092；2. 土木工程防灾国家重点实验室(同济大学)，上海 200092)

主要对铝合金构件采用高强螺栓牙板连接进行初步试探性的理论分析和试验研究.分析结果表明：连接承载力与螺栓预压力、板件厚度、牙纹规格等因素有关，并初步得出了承载力的计算公式.进行了4组铝合金构件高强螺栓牙板连接的抗剪承载力试验，试验结果表明：高强螺栓牙板连接具有变形小、承载力高等特点，而且较普通的摩擦型高强螺栓连接承载力有明显提高，主要是因为“牙板”增大了受力方向的抗滑移系数.

铝合金； 高强螺栓牙板连接； 抗剪承载力试验

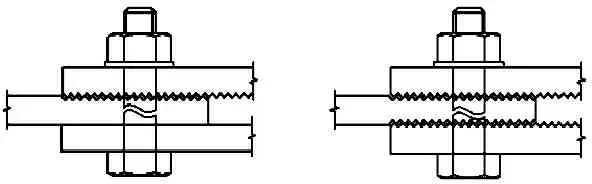
铝合金自重轻、耐腐蚀、易回收，在建筑结构中应用日益广泛.铝合金构件的主要连接方式有焊接和螺栓连接，而焊接将导致铝合金焊接热影响区的材料强度下降到母材强度的60%以下，因此工程中除特殊情况外大多都采用螺栓连接.螺栓连接对于安装精度的要求较高，而且一般摩擦型高强螺栓连接的承载力对被连接构件表面的粗糙度要求较高，当构件表面摩擦系数的离散性较大时，螺栓的利用效率就受到了制约.高强螺栓牙板连接(图1)作为一种创新型的连接技术，具有传力可靠、承载力高、变形较小等优点，可用于铝合金结构的连接.

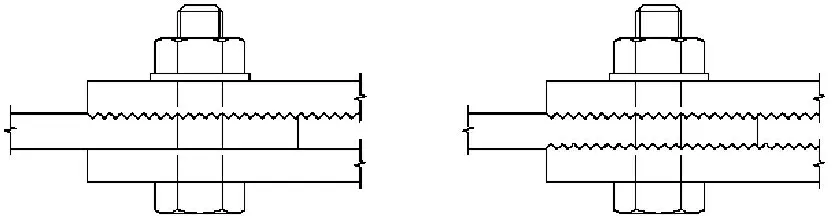
图1高强螺栓牙板连接示意图

Fig.1High strength bolted zigzag-plate connections

高强螺栓牙板连接是在传统高强螺栓连接的基础上，将连接件与被连接件的接触面改进为牙纹形，即“牙板”.由于其工作时螺栓不受剪，因此其螺栓孔可设计为长圆孔，使安装精度的要求大大降低；此外，其承载力将由于牙板的齿间预压力和齿间咬合摩擦力而大大提高.

1　理论分析

1.1传力机理

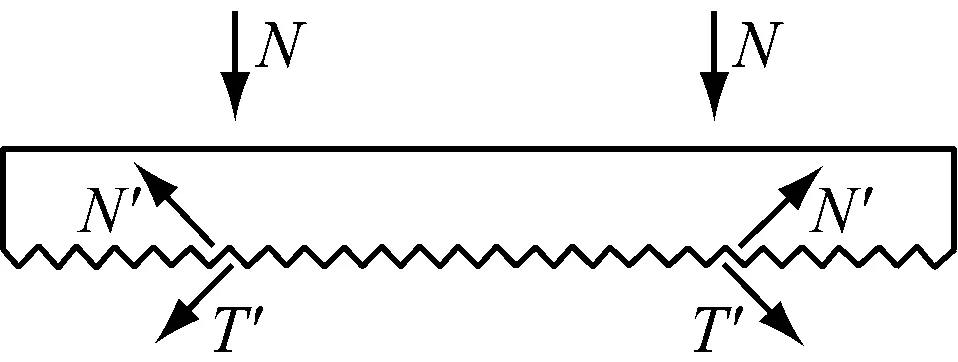
高强螺栓牙板连接的受力原理与摩擦型高强螺栓连接类似，都是通过旋紧螺栓使螺杆产生预压力压紧构件接触面，靠接触面的摩擦力来阻止其相互滑移，以达到传递外力的目的.如图2所示，在预压荷载N作用下，A、B和C三块板件得以紧密接触，令板件的摩擦面间拥有抗滑移强度，从而可以抵抗外荷载T.外荷载T通过牙板，一部分靠与接触齿面平行的摩擦力f′传递，一部分靠与接触齿面垂直的压力N′传递，最终全部传递至板件A和B.

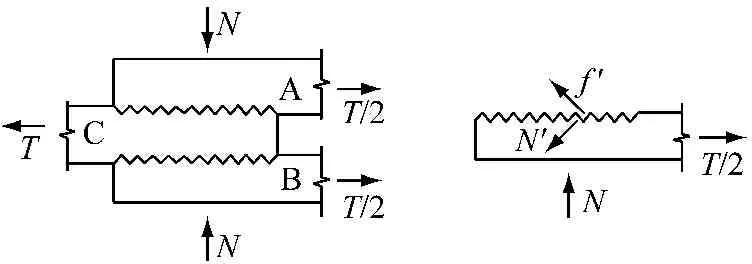
图2高强螺栓牙板连接受力简图

Fig.2Forces in HSBZP Connections

图2仅将螺栓的作用简化为一个大小为N的预压力；事实上，除提供预压力外，螺栓还相当于一个置于板件A和B外表面的弹性约束，以致预压力的值将随连接的变形而改变.当连接处于摩擦失效的临界状态时，并不会立即失效，因为螺栓本身的刚度将限制板件之间的滑移，此后，荷载T的增量将继续传至板件A和B，而随之增大的N′最终将传至螺栓使螺栓受到的拉力进一步增大.

1.2破环形式

根据受力机理，高强螺栓牙板连接可能发生以下几种破坏形式：①齿间滑移破坏(图3a)、②净截面强度破坏(图3b)、③螺栓受拉破坏(图3c)、④牙纹承压破坏和⑤牙纹受剪破坏.

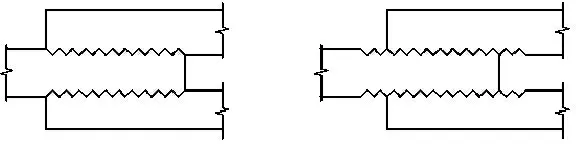
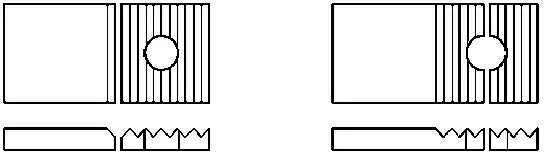
a 齿间滑移破坏

b 净截面强度破坏

c 螺栓受拉破坏

图3破坏形式示意图

Fig.3Failure mode configurations

当牙纹深度较大且刚度较大或螺栓分布不合理时，在齿间滑移发生到一定程度后可能会由于连接的过度变形而使螺栓被拉断；当牙纹数量较少且咬合并不充分密实时，可能只有部分牙纹在受力，此时将发生牙纹承压破坏；当牙纹数量较少、牙纹角度较大且咬合并不充分密实时，板件可能出现牙纹受剪破坏.

所以，当牙纹深浅适中、牙纹数量和牙纹角度合适且螺栓排布得当时，后三种破坏形式不会发生.因此，可以通过构造要求来限制牙板的几何参数和螺栓的排列间距及预压力大小，以此来排除后三种破坏发生的可能性；即：设计时只需对前两种破坏形式的承载力进行计算即可.

1.3构造要求

由于铝合金结构与钢直接接触时，会发生接触腐蚀.因此，钢螺栓需进行电镀锌或浸镀锌等表面处理，以确保不发生腐蚀.另外，当高强螺栓的抗拉强度超过铝合金构件抗拉强度的3倍时，需采用较大直径的硬质垫圈，以确保螺栓预紧力可以较为均匀地传递至构件.更重要地，为了防止连接出现螺栓受拉破坏、牙纹承压破坏和牙纹受剪破坏，需要对螺栓的容许间距、预拉力大小和牙板的几何尺寸进行相关限制：从受力性能来看，若牙纹角度太小或深度太浅，则牙纹的齿间咬合作用就不太明显，若牙纹角度太大或深度太大，则牙板的净截面强度无法得到保证；从施工便利性来看，牙纹整体尺寸过大会使得安装调整幅度变大.所以，适当的牙纹角度和牙纹深度对于整个连接而言是不可或缺的.

对于螺栓的容许间距和预拉力大小，可参照摩擦型高强螺栓连接中的相关规定[1-2].对于牙板，主要限制其牙纹角度和牙纹深度，本文初步选定其限值见表1.

表1　牙板各参数的最大、最小限值

注：h为被连接板件中较薄板件的厚度.

1.4承载力计算

满足了适当的构造要求后，设计时只需对前两种的破坏形式的承载力进行计算即可.

1.4.1抗滑移承载力

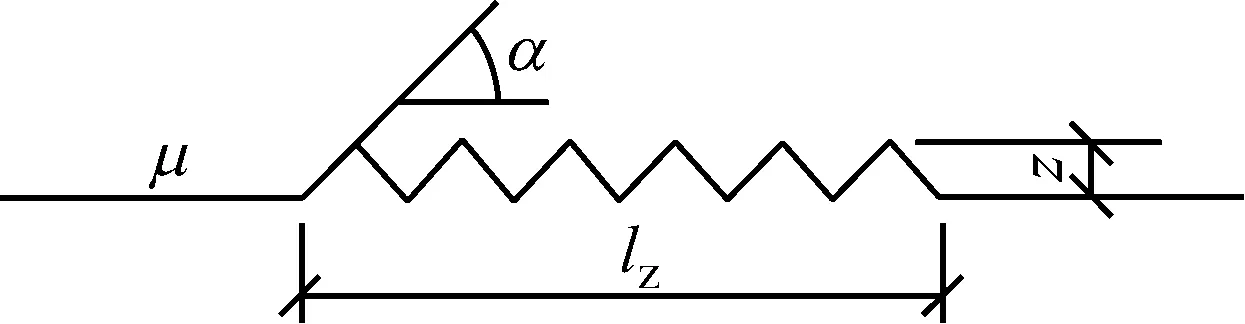
取其临界状态受力简图如图4所示.当连接处于滑移破坏临界状态时，螺栓对板件的压力为N，板件所受拉力为T，各板件之间将发生沿齿面的滑移，牙纹角度为α，材料本身的抗滑移系数为μ′.

根据投影定理，可求得：

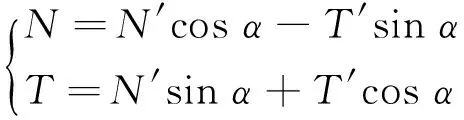
(1)

根据静力摩擦公式，当T=μ′N′时，发生滑移破坏，对应的滑移临界荷载为

(2)

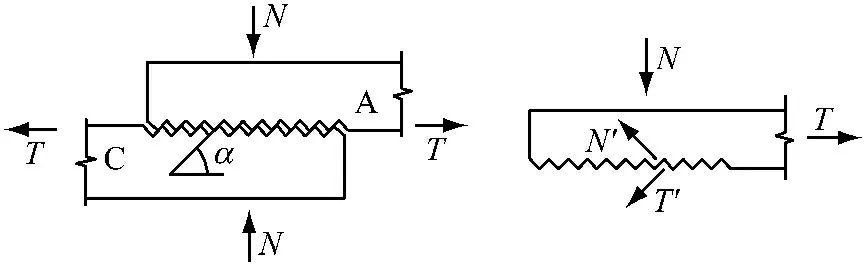
图4滑移破坏临界状态下的受力简图

Fig.4Forces in connections of plate shear dislocation

事实上，发生齿间滑移破坏时，牙纹的角度α及螺栓对板件的压力N都将由于受力而发生改变：牙纹的角度α将随着荷载增加逐渐变小，螺栓对板件的压力N将随着荷载增大到某一定值后逐渐随荷载增大，而破坏时的压力N与牙纹的深度z有关，z越大，N越大.

偏于安全地可以取α=βα0，N=Np，其中，α0为初始牙纹角度，β为角度变形系数，Np为螺栓设计预紧力.β与材料的弹性模量E、螺栓预紧力Np等因素都有关；其值越小，临界荷载T也将越小；但若牙纹变形超过一定范围，则连接可判定为发生了牙纹承压破坏或牙纹剪切破坏.对于铝合金构件，可以定性地取β=0.95，此处考虑5%的角度变形已经足够安全.

所以，对于齿间滑移破坏，其破坏时的承载力可偏于安全地按式(3)计算：

(3)

对于单面牙纹连接，其承载力可按式(4)计算：

(4)

对于双面牙纹连接，其承载力可按式(5)计算：

(5)

式(3)—(5)中：T为连接破坏时的承载力；n为高强螺栓数量；nf为摩擦面数量，取2；μ′为材料本身的抗滑移系数；β为牙纹角度变形系数，可取为0.95；α0为初始牙纹角度；Np为高强螺栓的预紧力.

1.4.2构件净截面承载力

截面的削弱来源于牙纹凹陷与螺栓孔两部分，两处截面均可能发生净截面强度破坏，如图5所示.

I-I截面(首个牙纹凹陷处的截面)的承载力计算公式为

(6)

式中：T为连接破坏时的承载力；AI为I-I截面的截面积；fy为板件的抗拉强度.

图5　削弱截面示意图

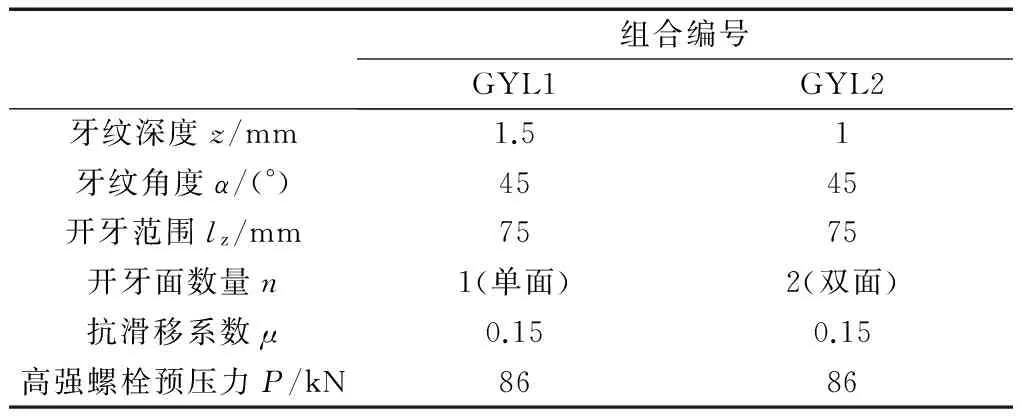
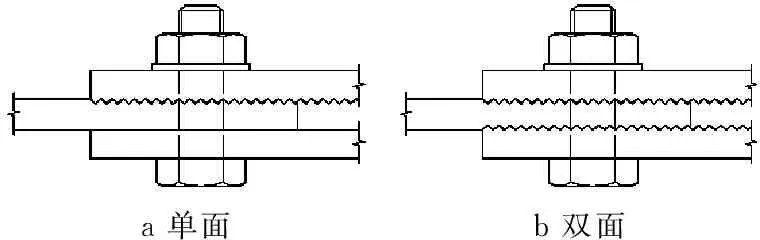
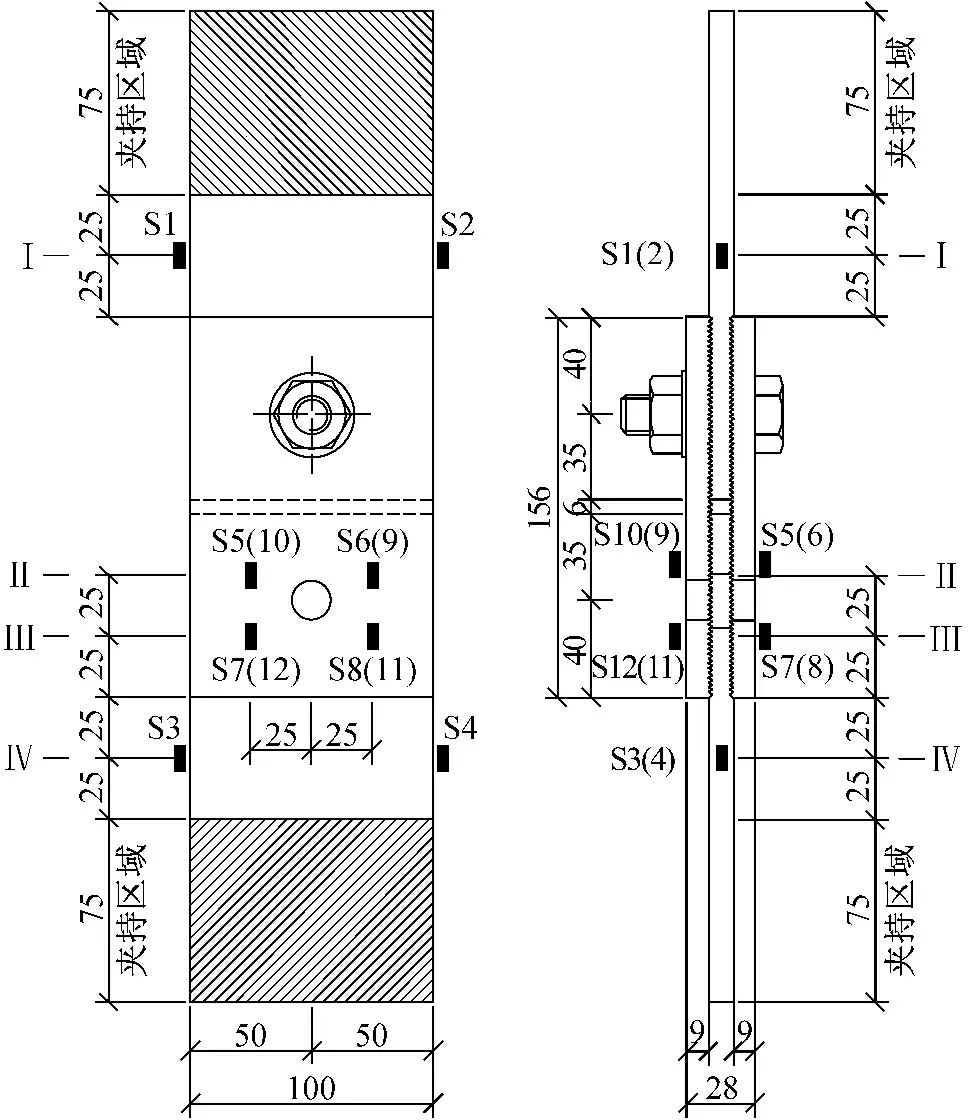
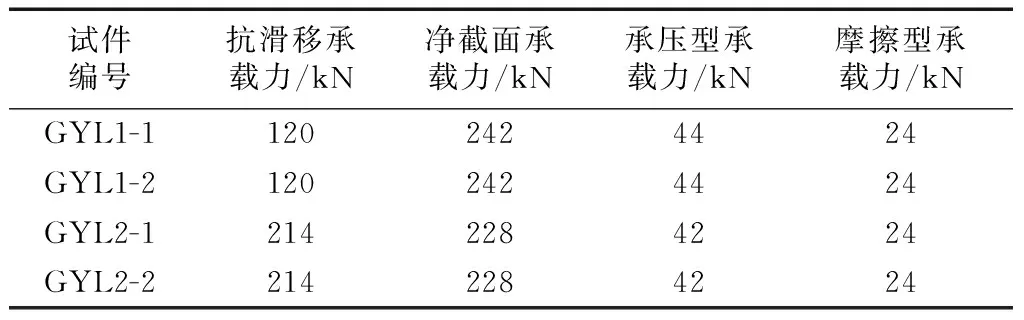
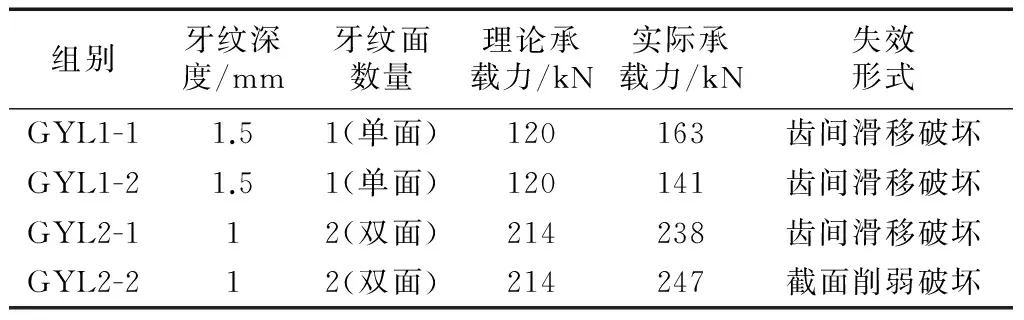
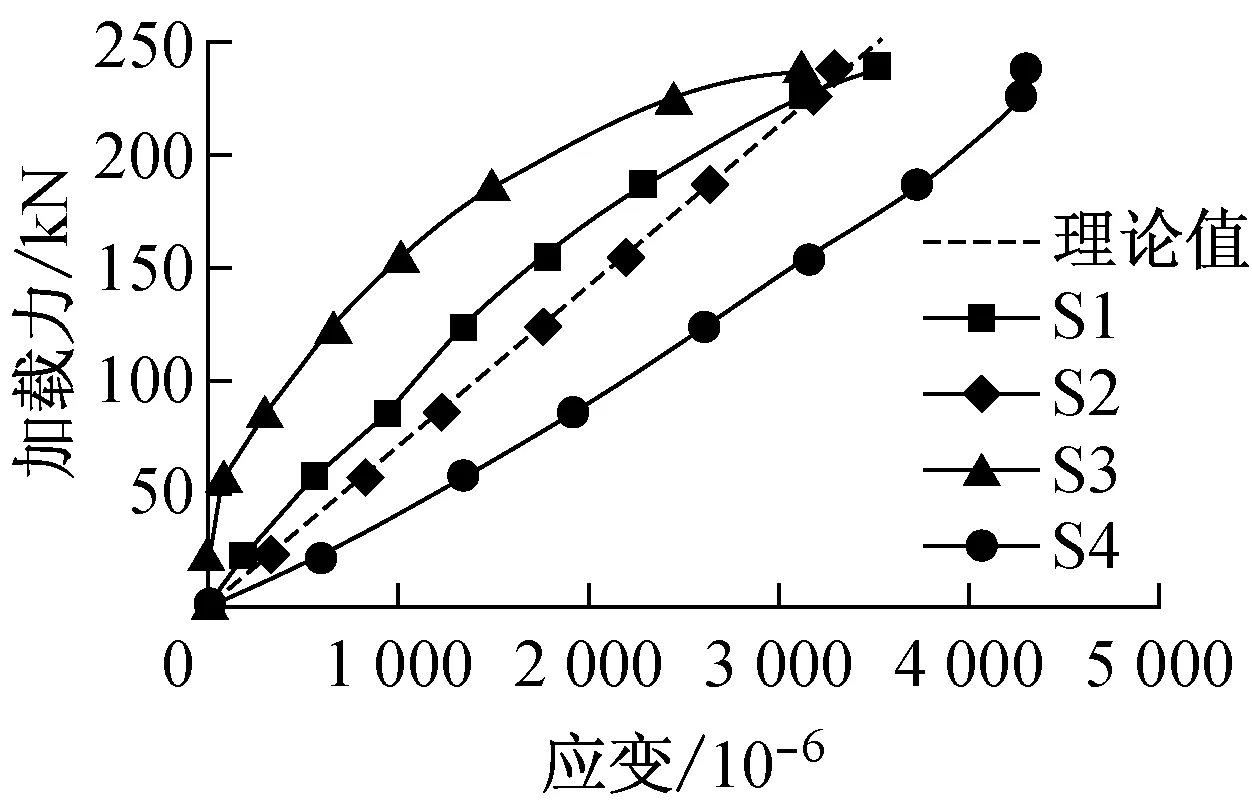
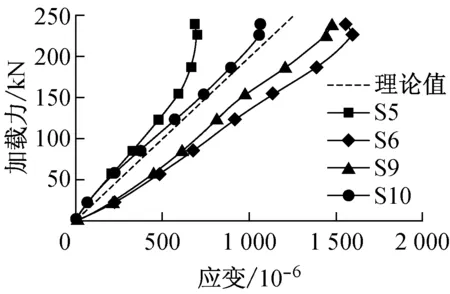
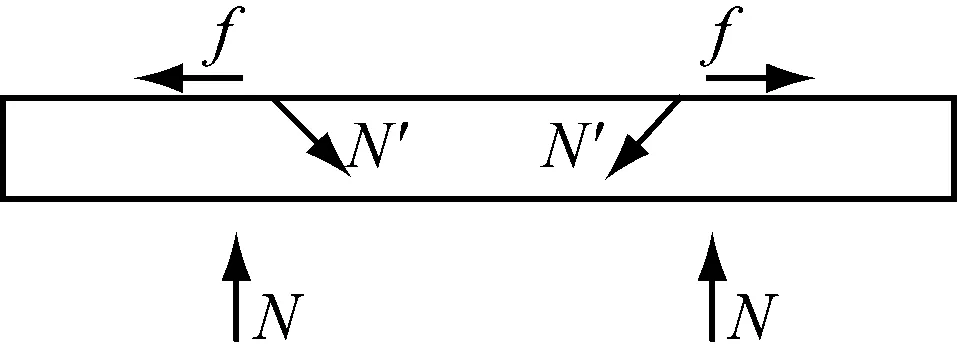
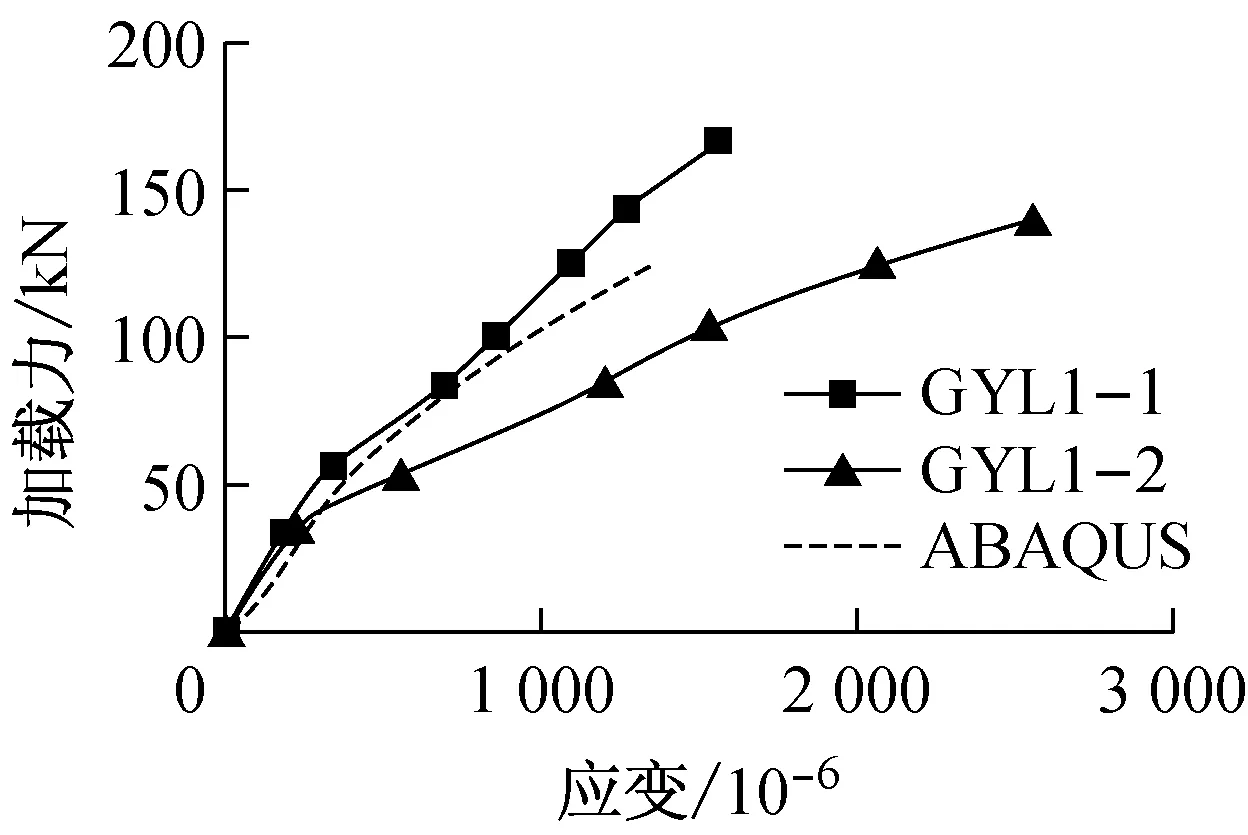
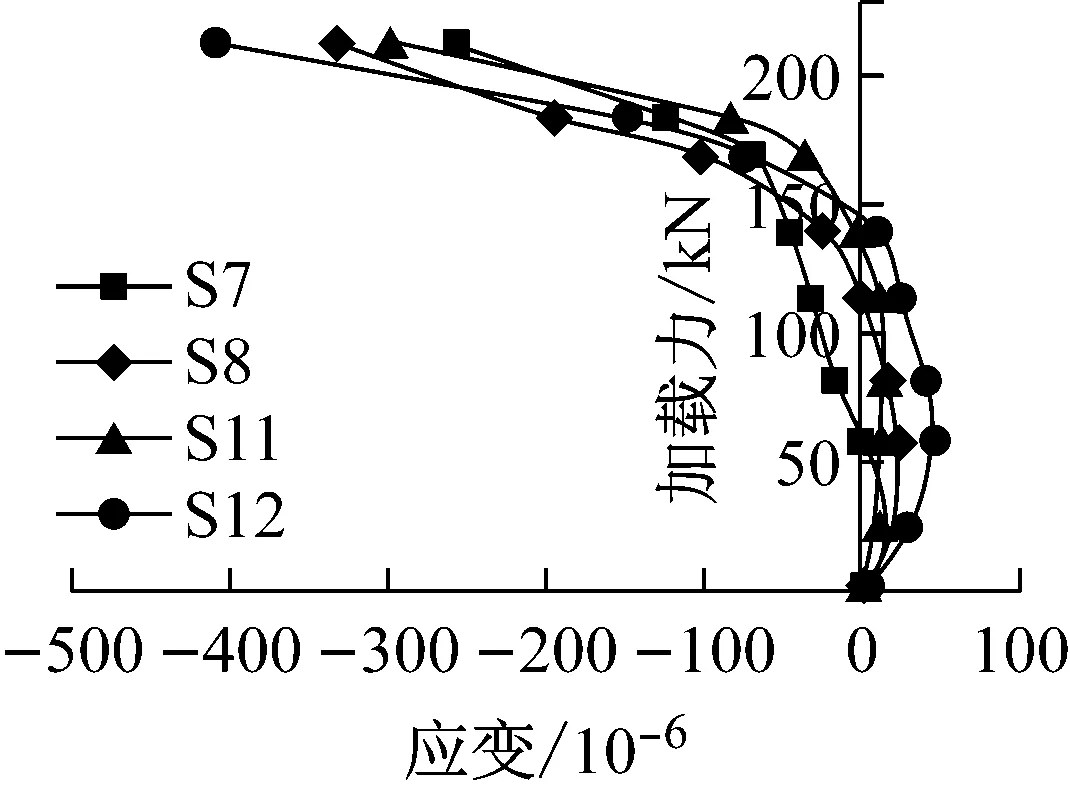
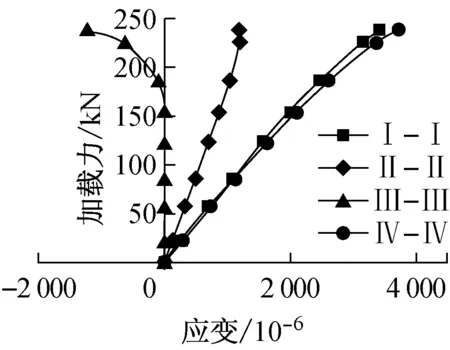
除I-I截面外，II-II截面(第一排螺栓孔处的截面)也是危险截面之一.但在这个截面上，连接所传递的轴荷载T已有一部分由孔前的牙板传递，所以净截面上的荷载Tn

设连接的螺栓数为n，所计算截面(最外列螺栓处)上的螺栓数为n1，则构件净截面所受的力为

(7)

II-II截面的承载力计算公式为

(8)

式中：An为II-II截面的截面积；fy为板件的抗拉强度.n1为II-II截面上的高强螺栓数量；n为高强螺栓数量.

所以，截面削弱破坏时的临界荷载为式(6)和(8)中较小的值，即：当荷载T达到此较小值时，连接将发生净截面强度破坏.

2　试验研究

本文通过4组试验来探究铝合金构件高强螺栓牙板连接在给定参数下的承载性能.所谓的给定参数包括牙纹深度z，牙纹角度α，开牙范围lz，开牙面数量n，抗滑移系数μ和高强螺栓预压力P等.本试验取两种参数组合，每种参数进行两组试验，试验参数见表2.牙板参数示意如图6所示.高强螺栓牙板连接如图7所示.

2.1试件设计

4组试件分别命名为GYL1-1、GYL1-2、GYL2-1和GLY2-2，表3给出了所有试件的具体信息.表中，10.9 SM16×50表示高强度螺栓性能等级为10.9S，螺栓公称直径16 mm，螺杆长度为50 mm.l,b,h分别为板的长度、宽度和厚度.

图6　牙板参数示意图

组合编号GYL1GYL2牙纹深度z/mm1.51牙纹角度α/(°)4545开牙范围lz/mm7575开牙面数量n1(单面)2(双面)抗滑移系数μ0.150.15高强螺栓预压力P/kN8686

a单面b双面

图7高强螺栓牙板连接示意图

Fig.7High strength bolted zigzag-plate connections

每组试件由两块被连接板和两块连接板经两个高强螺栓连接而成，如图8所示.高强螺栓采用10.9S级别M16×50大六角头高强螺栓，拟施加86 kN预紧力，安装时分两次用扭矩扳手拧紧.初拧扭矩值135 N·m，终拧扭矩值275 N·m.

表3　试件尺寸一览表

图8　试件组装示意图

2.2测点布置

每组试件布置12个应变片(S1～S12).S1～S2 (S3～S4)用于测量上(下)部被连接板件在施力处的应力情况；S5～S8(S9～S12)用于测量前(后)盖板在螺栓孔附近的应力情况；各测点具体位置如图9所示.对于单面牙纹连接，S5～S8所在盖板为平板.

图9测点布置示意图

Fig.9Measuring point arrangement of specimens

2.3材性试验

根据《金属材料拉伸试验第1部分：室温试验方法》GB/T 228.1—2010的相关要求[3]，本试验制作了三根材性试件，试验前后图片如图10所示，图中，a,b,c为试件编号.试验结果汇总见表4[4-5].

图10　试验前后的拉伸试样

注：后文理论承载力均以平均值为依据进行计算.

2.4承载力估算

按照式(4)—(5)和式(7)—(8)，代入试件的几何尺寸及材性试验结果，算得各试件理论承载力见表5.

表5　承载力估算结果

注：承压型承载力和摩擦型承载力仅供对比参考，连接的理论承载力取抗滑移承载力和净截面承载力的较小值.

2.5加载方案

本试验采用100 t万能试验机进行单调加载：加载初期控制应力增长速率为6 MPa·s-1，接近破坏时控制位移速率为0.5 mm·min-1.若试件出现滑移破坏，则继续加载至螺栓受剪破坏或板件孔壁承压破坏；若试件出现其他破坏形式，则结束试验.

3　试验结果

GYL1-1、GYL1-2的试验参数完全相同，同为牙纹深度为1.5 mm的单面牙板连接.GYL1-1在超出理论强度大约30%后于下部连接处发生滑移破坏，之后试件还可继续承载，但承载力降低至100 kN左右；GYL1-2在超出理论强度大约15%后于下部连接处发生滑移破坏，之后试件还可继续承载，但承载力降低至100 kN左右.失效形式如图11a和图11b所示.

GYL2-1、GYL2-2的试验参数完全相同，同为牙纹深度为1 mm的双面牙板连接.GYL2-1在超出理论强度大约10%后于下部连接处发生滑移破坏，之后试件还可继续承载，但承载力降低至50～100 kN之间；GYL2-2在超出理论强度大约15%后于下部连接处发现被连接板于薄弱界面处受拉破坏.这两组试验理论上应发生相同的失效形式，但是由于其抗滑移承载力和净截面承载力相近(由估算结果可知)，因此两种破坏形式出现的随机性较大.失效形式如图11c和图11d所示.

aGYL1-1bGYL1-2cGYL2-1dGYL2-2

图11各种破坏形式

Fig.11Failure modes

各组试验承载力与失效形式汇总见表6.

表6　各组试验承载力与失效形式

4　数据分析

通过数据采集装置，本试验可得到一系列荷载、应变以及支座位移的数据.将应变片S1和S2所在断面定义为截面I-I，将S5、S6、S9和S10所在断面定义为截面II-II，将S7、S8、S11和S12所在断面定义为截面III-III，将S3和S4所在断面定义为截面IV-IV，如图9所示.

图12描述了GYL2-1两块被连接板I-I和IV-IV截面上测点的荷载-应变关系.不难看出，随着荷载增大，两侧测点均受拉，且应变也不断增大.S1与S2同为上侧被连接板的两个测点，S3与S4同为下侧两个测点.理论上，若被连接板件尺寸标准、安装在试验机上时是完全对中且连接处受力均匀，此4个测点的应变应该等于理论值.而图12所示曲线有所偏离理论值，这可能是以下三部分原因导致：①板件厚度不均匀导致夹头夹持力不均匀，使得拉力不是均匀分布在板件宽度方向；②牙板连接的咬合度以及预紧力沿板件宽度方向分布不均匀，进而导致传力不均匀；③安装时试件没有完全对中.

图12　GYL2-1荷载-应变曲线(S1～S4)

图13描述了GYL2-1在II-II截面上4个测点的荷载-应变关系.图中理论值指的是：假定在此截面荷载已充分传至连接板上时，连接板上应有的应变.从图中可以看到，同一块板上的两个测点，其曲线一条低于理论值，一条高于理论值，这应该和之前提及的受力不均匀有关.但就其总体情况而言，此时连接板已开始和被连接板一同受力，说明牙板确实可以将荷载由被连接板传递至连接板.

图13　GYL2-1荷载应变曲线(II-II截面)

图14描述了GYL1-1在II-II截面上测点的荷载-应变关系.对于本组单面牙板连接试验，一侧为带有牙纹的牙板(S9与S10)，一侧为平板(S5与S6).由图可见，平板上测点的应变一直随荷载增加而增加，牙板上测点的应变先是随荷载增加而增加，到达一定值之后出现减小的趋势并最终进入受压状态.

考察牙板的受力情况，其受力图简化如图15a所示.在荷载达到40 kN以前，可以认为N′=T′，所以没有弯矩产生，牙板与平板共同受力且分配到的荷载相当.但当荷载超过40 kN以后，N′>T′，这将使板件产生相应的弯矩，使板件上部受压，下部受拉，此时板件在纵向进入拉弯状态，从而使相应测点的应变数值开始减小.随荷载继续增加，N′>T′的趋势越发明显，板件上部受压的趋势也将越发明显；同时，N也将随着N′的增大而增大，这使下部平板的预压力增大而增大了其抗滑移承载力.

图14　GYL1-1荷载应变曲线(II-II截面)

a 牙板受力简图

b 平板受力简图

对于下部的平连接盖板，其受力图简化如图15b所示.与牙板相对的，当N′开始加速增长时，平板也将出现受弯的趋势，并且这个附加的弯矩将使得两个螺栓孔之间的测点受拉，进而导致测点拉应变增长速率加快.

为了更好地解释这种附加弯矩效应，本文建立了与试验试件规格相同的ABAQUS模型，如图16所示.考虑结构及荷载的对称性，取左半部分进行建模，模型自上而下由5个构件组成：垫圈、牙板、被连接板、平板、垫圈.分别定义各接触面的切向性质和法向性质：法向“硬接触”，认为可以传递压应力而无法传递拉应力；切向考虑抗滑移系数为0.2且与接触面压应力成正比的摩擦力.预压力视为施加在两端垫圈表面的均布受压荷载，连接受到的拉力视为施加在被连接板左侧端部边界的均布受拉荷载.加载过程采用力控制的分步加载.

图17和图18为通过模型计算得到的相同测点处的荷载-应变曲线与试验数据的对照曲线.从图中可以看出，数值分析的结果与试验所得到的结果在受力趋势上相当一致.

图16　ABAQUS计算模型简图

图17　连接盖板(牙板)荷载应变曲线

图18　连接盖板(平板)荷载应变曲线

对于III-III截面，4组试验的荷载-应变曲线趋势大致相同，图19所示为GYL2-2的测点数据.在荷载达到150 kN之前，本截面基本不受力，之后随着荷载继续增大，截面开始受压.对比之前的理论假定，假定荷载由牙板沿长度方向渐渐开始传递，由于本截面靠近板件边缘，其分担到的荷载并不大，这是合理的；之后截面受压是因为在板件受荷时，被连接板与连接板间有相对运动的趋势，这导致III-III截面附近的连接板有一种“被顶开”的趋势，由于螺栓设置在III-III截面上方，无法在此处对这种趋势很好地加以约束，导致连接板在此处呈现“端部翘起”的现象，进而使牙板在此截面以下的咬合近乎失效；而由于“端部翘起”效应，这些失效的牙纹应承受荷载就由螺栓孔附近的牙纹代替它们受载，代替受载范围可能是以螺栓为中心的环形区域.从进而导致测点处产生压应变.由于4组试验在这4个测点上的结果较为一致，可以认为：排列螺栓时，限制最外侧螺栓孔至构件边缘的最大距离是非常有必要的，否则，将导致边缘区域的无效咬合以及无效摩擦.

将同一个截面上所有对称测点的应变值的平均值取为该截面的平均应变，GYL2-1试件中各截面的荷载-均值应变曲线整理如图20所示.可见，I-I、IV-IV截面上的荷载由被连接板件独自承担；进入连接区域后，未到达螺栓孔截面的III-III截面并没有和被连接板件共同承载，但到达II-II截面时，荷载已充分传递至连接板.

图19　GYL2-2荷载应变曲线(III-III截面)

图20　GYL2-1各截面荷载应变曲线

5　结论

本文针对铝合金构件高强螺栓牙板连接进行了4组试验，结合理论分析，可得出以下结论：

(1)高强螺栓牙板连接确能有效应用于铝合金结构，在相同的表面处理以及相同的螺栓设置和排列下，其抗滑移承载力较摩擦型高强螺栓连接有显著提高，提高倍数与构件本身的抗滑移系数以及牙纹角度有关.

(2)高强螺栓牙板连接一共可能出现5种破坏形式：齿间滑移破坏、截面削弱破坏、螺栓受拉破坏、牙纹承压破坏以及牙纹受剪破坏.通过构造要求可以避免连接发生后三种破坏形式，并通过承载力计算以确保不发生前两种破坏形式.

(3)通过试验，验证了本文提出的理论计算公式的可靠性.理论公式计算出的承载力都略小于试验测得的承载力，说明公式是可靠且偏于安全的，能用于该类连接设计承载力计算.

(4)试验研究发现单面牙纹高强螺栓牙板连接在承载后期出现“附加弯矩”，这种附加弯矩并不对承载力造成显著影响，但使用双面牙纹高强螺栓牙板连接时，其结构性能的对称性更好.

[1]沈祖炎, 陈扬骥, 陈以一, 等. 钢结构基本原理[M]. 北京: 中国建筑工业出版社, 2005.

SHEN Zuyan, CHEN Yangji, CHEN Yiyi,etal. Fundamental of steel structures[M]. Beijing: China Architecture& Building Press, 2005.

[2]中华人民共和国建设部. GB50017—2003 钢结构设计规范[S]. 北京: 中国建筑工业出版社, 2003.

Ministry of Construction, the People’s Republic of China. GB50017—2003 Code for design of Steel structures[S]. Beijing: China Architecture & Building Press, 2003.

[3]国家质量监督检验检疫总局和标准化管理委员会. GB/T 228.1—2010 金属材料拉伸试验第1部分：室温试验方法[S]. 北京: 中国标准出版社, 2010

General Administration of Quality Supervision, Inspection and Quarantine, the People’s Republic of China and Standardization Administration of the People's Republic of China. GB/T228.1—2010 Metallic materials-Tensile testing-Part 1: Method of test at room temperature[S]. Beijing: Standards Press of China, 2010

[4]中华人民共和国建设部. GB50429—2007 铝合金结构设计规范[S]. 北京: 中国建筑工业出版社, 2007.

Ministry of Construction, the People’s Republic of China. GB50429—2007 Code for design of aluminum alloy structures[S]. Beijing: China Architecture & Building Press, 2007.

[5]郭小农. 铝合金结构构件理论和试验研究[D]. 上海: 同济大学, 2006.

GUO Xiaonong. Theoretical and experimental research on the aluminum alloy structure members[D]. Shanghai: Tongji University, 2006.

[6]EN1999-1-1：2000 Eurocode 9：Design of aluminum structures-General rules and rules for buildings [S]. Brussels: European Committee for Standardization, 2000.

[7]BS8118-1：1991 Structural use of aluminum：Code of practice for design [S]. London: British Standard Institution, 1991.

[8]Aluminum Association. Aluminum design manual [S]. [S.l.]: Aluminum Association, 1994.

Experimental Research on High Strength Bolted Zigzag-Plate Connections of Aluminum Alloy Members

JIANG Shouchao1,2, YE Zhongnan1,2, GUO Xiaonong1

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering(Tongji University)，Shanghai 200092, China)

This paper focuses on the premature theoretical analysis and experimental research of high strength bolted zigzag-plate connections of aluminum alloys. It is found that the factors affecting the bearing capacity of the connection are prestress in boltes, thickness plates and zigzag dimensions. Shear-resistant capacity tests were conducted for aluminum alloy component with high strength bolted zigzag-plate connections (HSBZP). The test results showed that high strength bolted zigzag-plate connections had copious advantages including but not limited to reliable force transferring, comparatively slight deformation and much higher capacity than regular slip-critical bolted connections, The zigzag plates increased the slip resistance of the connection.

aluminum alloy; high strength bolted zigzag-plate connections; shear-bearing capacity tests

2015-11-11

科技部国家重点实验室基础研究资助项目(SLDRCE15-B-04)

蒋首超(1971—)，男，工学博士，主要研究方向为金属结构及工程结构抗火.E-mail：scjiang@tongji.edu.cn

TU395

A