有限体积法定价跳扩散期权模型

甘小艇, 殷俊锋, 李　蕊,3

(1. 同济大学 数学系, 上海 200092； 2. 楚雄师范学院 数学与统计学院，云南 楚雄 675000;3. 嘉兴学院 数理与信息工程学院, 浙江 嘉兴 314001)



有限体积法定价跳扩散期权模型

甘小艇1,2, 殷俊锋1, 李蕊1,3

(1. 同济大学 数学系, 上海 200092； 2. 楚雄师范学院 数学与统计学院，云南 楚雄 675000;3. 嘉兴学院 数理与信息工程学院, 浙江 嘉兴 314001)

考虑有限体积法求解Kou模型下美式跳扩散期权.基于线性有限元空间,构造了向后欧拉和Crank-Nicolson两种全离散有限体积格式,并采用简单高效的递推公式对偏微分积分方程中的积分项进行逼近.针对美式期权离散得到的线性互补问题(LCP),采用模超松弛迭代法(MSOR)进行求解,并证明了H+离散矩阵下算法的收敛性.数值实验表明,所构造的方法是高效而稳健的.

有限体积法;Kou跳扩散期权模型; 线性互补问题; 模超松弛迭代法

在金融经济学中, 标准的Black-Scholes定价方程是最成功也是使用最广泛的期权定价工具[1]. 然而实证分析结果显示: 标准的Black-Scholes假设——标的资产价格服从波动率为常数的对数正态分布——与实际的市场观察并不一致. 通常将这一现象称作波动率偏态或波动率微笑, 该现象如今在许多主要金融市场中都存在. 为了解决波动率微笑的存在问题, 人们提出了Black-Scholes模型的各种演变形式. 常见的有: 随机波动率模型、带跳跃过程模型、非确定波动率模型、市场状态转换模型及确定性波动率模型等. 其中Merton[2]和Kou[3]跳扩散模型所隐含的波动率曲线与市场中观察到的波动率微笑十分接近, 吸引了众多国内外学者和专家的广泛关注和研究[4].

近年来, 人们对跳扩散期权定价问题作了大量研究工作.Tavella和Randall[5]给出了欧式Merton跳扩散模型的隐式有限差分格式, 并提出了一种用于求解稠密系统的迭代格式.Andersen等[6]中构造了欧式跳扩散模型的交替方向(ADI)格式, 并引入快速傅里叶变换(FFT)对积分项进行逼近, 计算量为O(mlogm), m表示空间节点个数. 此后,d′Halluin等[7-8]结合积分项的FFT逼近, 同时对欧式和美式Merton和Kou模型进行了研究. 针对欧式期权, 采用文献[5]中的迭代格式进行求解, 并对该迭代格式进行了收敛性分析; 而针对美式期权, 则采用惩罚方法进行求解. 为了降低偏微分积分方程(PIDE)中积分项的计算量,Toivanen等[9-10]构造了简洁高效的线性插值逼近, 并从理论上证明了该插值逼近的二阶收敛精度且离散矩阵为M矩阵. 特别地,根据Kou模型中对数双指数分布函数的特点,Toivanen在文献[9]中针对积分项给出了具有最优计算量的递推公式, 仅需O(m). 另外, 为克服Black-Scholes偏微分方程固有的对流占优特性而引起的计算困难,Zhang等[11-12]讨论了欧式和美式Merton以及欧式Kou跳扩散模型的拟合有限体积方法(Fittedfinitevolumemethod). 该方法主要是将经典有限体积方法结合特定的逼近技术对偏微分方程(PDE)进行离散. 美式期权定价的经典有限体积方法及其最新研究进展可参阅文献 [13-14].

定价美式期权另一重要任务是对离散得到的线性互补问题进行求解. 目前常见的求解方法主要有: 投影超松弛迭代法(PSOR)[15];算子分裂方法[16]和惩罚函数方法[17]. 近年来, 另一类重要的迭代方法——模方法, 得到了人们的广泛研究. 其数学思想在于将线性互补问题(LCP)转化成一系列线性方程组的求解. 通过将LCP转化成隐式不动点方程,Murty[18]最早提出了模迭代方法. 此后,Hadjidimos[19]和Dong[20]通过引入参数, 分别提出了非定常外推方法[19]和改进模方法[20], 加速了模方法的收敛速度. 通过将LCP转化成一类新的不动点方程,Bai提出了一类基于模分裂的迭代算法(modulus-basedmatrixsplittingmethods)[21]. 此方法利用适当的矩阵分裂可以得到一系列新的迭代方法, 如: 模超松弛方法(MSOR)等. 关于模方法的最新研究进展,可以参阅文献 [22-23].

本文研究Kou模型下跳扩散期权的有限体积法求解. 基于线性有限元空间, 首先构造了向后欧拉和Crank-Nicolson两种稳定的全离散格式. 其次, 采用文献[9]中的线性插值技术对PIDE(partialintegro-differentialequation)中的积分项进行逼近. 针对离散得到的线性互补问题,采用MSOR方法进行求解,并进一步建立H+离散矩阵矩阵下算法的收敛性. 数值实验表明,文中方法是有效且稳健的.

1　跳扩散期权模型

假设标的资产价格x满足如下随机微分方程：

(1)

式中:dx(t)/x(t-)为跳跃大小与跳跃前一个时刻的价格的比例;μ和σ分别为资产价格没有发生跳跃时的期望收益率和波动率；W(t)为标准的布朗运动；N(t)为强度为λ的泊松过程；{Vj}是一系列独立同分步的随机变量的集合, 并且服从对数双指数密度分布

(2)

其中α1>1,α2,p,q都是正常数, 且p+q=1.

由文献[9]可知,Kou模型下欧式跳扩散期权值v满足如下PIDE：

(3)

(4)

初值条件为

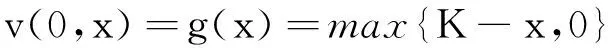
(5)

对于看涨期权, 边界条件为

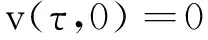
(6a)

(6b)

初值条件为

(7)

其中K为敲定价格.

另外,Kou模型下美式跳扩散期权可以通过求解如下互补问题得到：

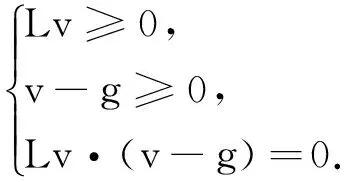
(8)

其中：

考察美式看跌期权, 初值条件为式(5), 边界条件为

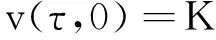
(9a)

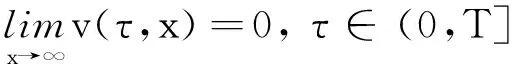
(9b)

为有限体积离散方便, 首先将方程(3)简化为如下变系数抛物型方程：

(10)

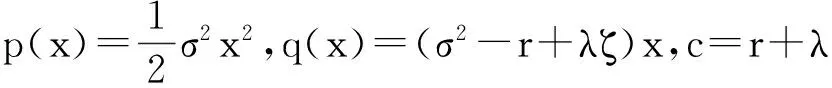
本文主要考虑美式看跌期权模型的有限体积离散, 看涨情况的处理相似.

2　积分项逼近及有限体积离散

期权定价问题是定义在无限的区域[0,∞)×[0,T]上, 为了采用有限体积求解, 必须把原问题限制在一个截断的区域[0,X]×[0,T]上, 其中X要取得足够大.

2.1积分项逼近

本小节中, 主要采用文献[9]中的线性插值技术和递推公式对方程(10)中的积分项

(11)

将Q分成两部分,Q=Q-+Q+, 其中：

(12)

(13)

接下来, 首先考虑Q-项的逼近. 在离散节点xi(i=1,2,…,m-1)处, 有：

(14)

其中：

(15)

在区间[xj,xj+1]上对v(z)进行线性插值处理, 可得：

(16)

其中：

(17)

经积分计算得：

(18)

(19)

同理, 对Q+项进行逼近, 即有：

(20)

其中：

(21)

(22)

在区间[xj,xj+1]上对v(z)进行插值处理并求积分, 则式(21)可以改写为

(23)

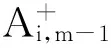
(24)

综上可知

(25)

其中v=(v1,v2…,vm-1)T为未知向量.

定理1[9]对任意给定的τ∈(0,T], 假设v(τ,x)关于x∈[0,X]二阶连续可导. 则当α2>0, α1>1时, 有如下结论成立：

定理2[9]矩阵R+λI是一个非负对角占优的Z矩阵, 即：

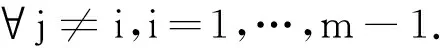
(26)

结合(16), 可得递推公式如下：

(27)

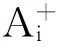
(28)

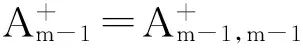
2.2有限体积格式

取试探函数空间Vh为相应于Th的线性有限元空间, 即Vh为满足下列条件的函数vh的集合:①vh∈C(E),vh(X)=0;②vh在每个Ei上是线性函数, 它完全由单元的两端点的值唯一确定. 由线性有限元空间的性质, 易知在单元Ei上有：

(29)

(30)

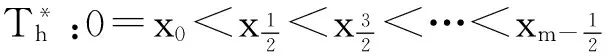
抛物型方程(10)的半离散有限体积格式为: 求vh=vh(τ,·)∈Vh使得:

(31)

或者等价地

(32)

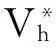
(33)

由式(30),(16)和(20), 则：

(34)

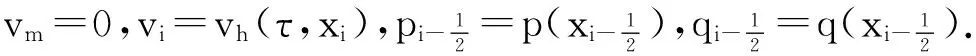
(35)

另外,时间项方向

(36)

由式(34)—(36)可得, 方程(31)对应的半离散矩阵形式为

(37)

其中S=P+R,R为积分部分离散所得稠密矩阵(25),P为非积分部分离散所得的三对角阵, 即:

且

式(37)的右端项为

证明首先对于P中的ai(i=2,…,m-1). 当i=2时,

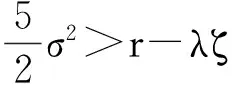
恒成立. 所以ai<0(i=2,…,m-1).

同理对P中的ci(i=1,…,m-2). 当i=1时, 有：

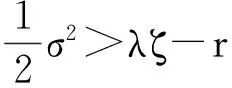
恒成立. 故ci<0(i=1,…,m-2).

最后对P中的bi(i=1,…,m-1). 当i=1和i=m-1时, 有：

另外, 当i=2,…,m-2时, 显然有

因此P-λI是一个严格对角占优矩阵, 即:

由此式可知, 对任意的i显然有(P-λI)i,i>0成立, 则定理得证.

由定理3.2和定理3.3可得如下推论.

(38)

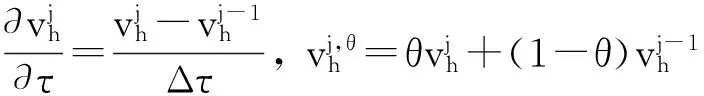
将式(38)写成矩阵形式：

(39)

由推论1可知, 下面推论2结论显然成立.

推论2说明了全离散系统(39)满足离散极大值原理且离散是单调的.

3.3线性互补问题

(40)

其中j=1,…,n, 向量g包含了收益函数g(x)在网格点处的函数值.特别地, 令z:=v(j)-g,A:=B,q:=Bg-Cv(j-1)-f,则式(40)变为标准的LCP

(41)

记为LCP(q,A), 本文主要采用模超松弛迭代法对其进行求解.

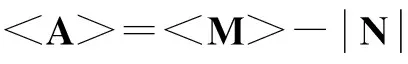
接下来, 建立MSOR方法求解Kou跳扩散期权定价模型的收敛定理.

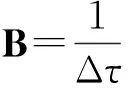
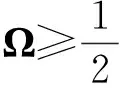
3　数值实验

用数值实验来验证文中方法的有效性.Kou模型参数取：

α2=3.077 5, p=0.344 5, q=0.655 5

(42)

且计算区域为[0,300]×[0,0.25]. 这里的模型参数与文献[8-10]中的取值相同.

首先, 表1给出了当取不同的网格剖分时,CN有限体积格式求解Kou模型下美式看跌期权所得的部分节点处的期权值, 并与文献[9]作比计较. 记m为时间方向离散网格数,n为空间方向离散网格数.从表中不难看出, 数值解随着网格剖分数的增大变得更加精确.

表1　美式Kou跳扩散看跌期权的期权值 (CN格式)

其次, 为了计算数值解的相对误差, 采用CN格式在网格(m,n)=(4 800,3 200)上求解美式看跌期权的价格作为参考解. 期权价格曲面如图1a所示. 图中还展示了当t=0时刻的期权值、Delta值和Gamma值. 从图中不难看出,数值结果是稳健的.

最后,比较PSOR方法和MSOR方法的求解时间, 平均迭代步数以及求解精度.

表2和表3中, 分别列出了BE和CN格式下PSOR和MSOR的平均迭代步数IT,CPU时间和相对误差Error. 由这两个表可以看出, 所有方法均随着网格剖分数的增大数值解变得更加精确,PSOR和MSOR方法的计算精度大致相当. 虽然PSOR的平均迭代步数略少于MSOR, 但是其所需的

表2两种方法的误差, 迭代步数和所需CPU时间 (BE格式)

Tab.2Comparisonoftwomethodsoniterationnumber,CPUtimeandError(BEscheme)

(m,n)PSORMSORITCPUError/10-6ITCPUError/10-6(50,25)8.90.043579.60.01357(100,50)8.90.181549.70.06154(200,100)9.90.7759.914.80.3159.9(400,200)16.86.2322.927.53.6422.9(800,400)31.9102.279.5153.664.089.51

CPU时间却比MSOR要多. 另外, 对比两个表格还可看出,CN格式的计算效率明显高于BE格式.在图2中, 还画出了MSOR和PSOR方法的CPU时间随着空间方向离散网格数m的变化曲线. 由图可以看出,PSOR比MSOR需要更多的CPU时间.

a 期权价格曲面

b 期权值

c Delta

d Gamma

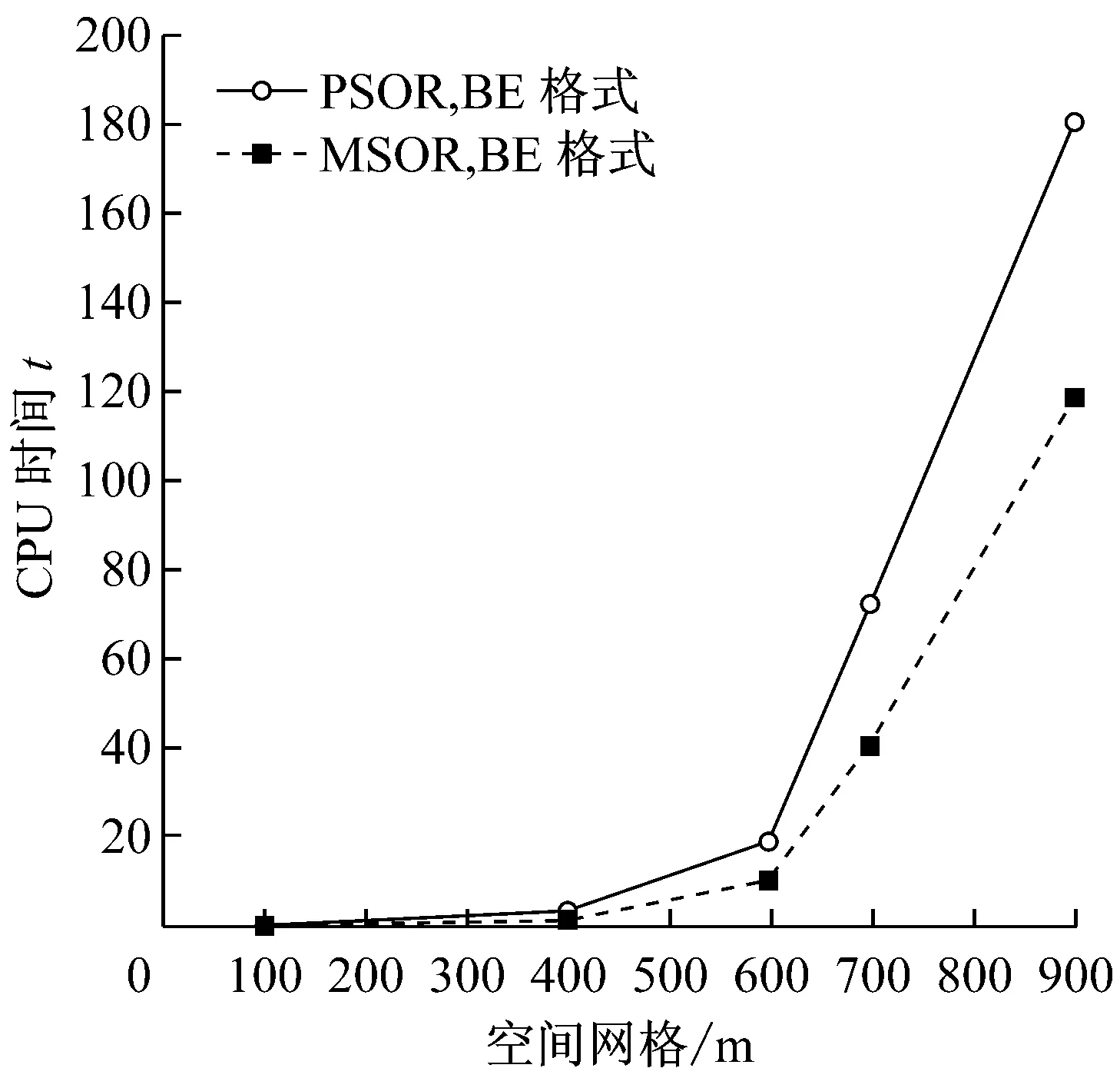
a BE格式

b CN格式

Tab.3Comparisonoftwomethodsoniterationnumber,CPUtimeandError(CNscheme)

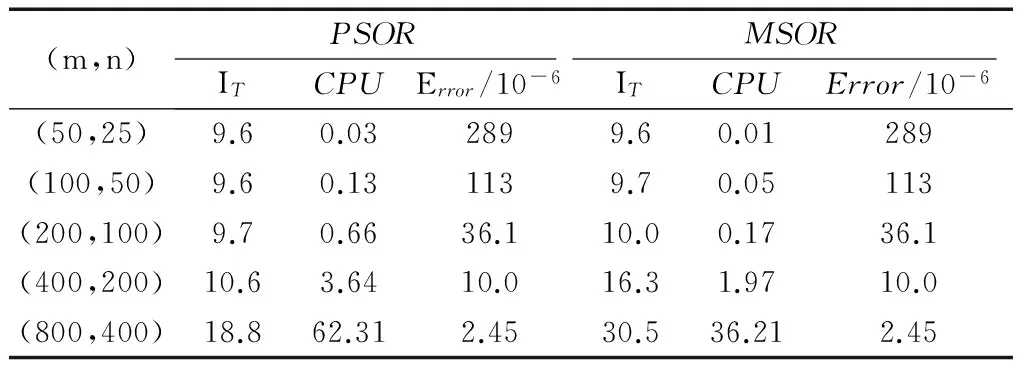
(m,n)PSORMSORITCPUError/10-6ITCPUError/10-6(50,25)9.60.032899.60.01289(100,50)9.60.131139.70.05113(200,100)9.70.6636.110.00.1736.1(400,200)10.63.6410.016.31.9710.0(800,400)18.862.312.4530.536.212.45

4　结论

本文主要研究了有限体积法定价Kou美式期权模型. 基于线性有限元空间, 构造了向后欧拉和Crank-Nicolson两种全离散有限体积格式, 针对Kou模型中的积分项, 采用文献[9]中高效的递归公式进行离散.针对美式期权定价离散得到的是一系列时间层上的线性互补问题, 采用模超松弛迭代方法进行求解, 并建立相应的收敛性定理. 数值实验验证了文中方法的高效性和稳健性. 但是，如何将文中方法推广至高维的美式跳扩散期权定价问题的求解, 例如Bates模型, 并进行相应的收敛性分析, 这仍需进一步的研究.

[1]BlackF,ScholesM.Thepricingofoptionsandcorporateliabilities[J].JournalofPoliticalEconomy, 1973, 81(3): 637.

[2]MertonRC.Optionpricingwhenunderlyingstockreturnarediscontinuous[J].JournalofFinancialEconomics, 1976, 3: 125.

[3]KouSG.Ajump-diffusionmodelforoptionpricing[J].ManagementScience, 2002, 48(8):1086.

[4]KouSG,WangH.Optionpricingunderadoubleexponentialjumpdiffusionmodel[J].ManagementScience, 2004, 50(7): 1178.

[5]TavellaD,RandallC.Pricingfinancialinstruments:Thefinitedifferencemethod[M].Chichester:JohnWileySons, 2000.

[6]AndersenL,AndreasenJ.Jump-diffusionprocesses:Volatilitysmilefittingandnumericalmethodsforoptionpricing[J].ReviewofDerivativesResearch, 2000, 4(3): 231.

[7]d'HalluinY,ForsythPA,LabahnG.ApenaltymethodforAmericanoptionswithjumpdiffusionprocesses[J].NumerischeMathematik, 2004, 97(2): 321.

[8]d'HalluinY,ForsythPA,VetzalKR.Robustnumericalmethodsforcontingentclaimsunderjumpdiffusionprocesses[J].IMAJournalofNumericalAnalysis, 2005, 25(1): 87.

[9]ToivanenJ.NumericalvaluationofEuropeanandAmericanoptionsunderKou'sjump-diffusionmodel[J].SIAMJournalonScientificComputing, 2008, 30(4): 1949.

[10]SalmiS,ToivanenJ.AniterativemethodforpricingAmericanoptionsunderjump-diffusionmodel[J].AppliedNumericalMathematics, 2011, 61(7): 821.

[11]ZhangK,WangS.Pricingoptionsunderjumpdiffusionprocesseswithfittedfinitevolumemethod[J].AppliedMathematicsandComputation, 2008, 201(1): 398.

[12]ZhangK,WangS.Acomputationalschemeforoptionsunderjumpdiffusionprocesses[J].InternationalJournalofNumericalAnalysisandModeling, 2009, 6(1): 110.

[13]甘小艇, 殷俊锋. 二次有限体积法定价美式期权 [J]. 计算数学, 2015, 37(1): 67.

GANXiaoting,YINJunfeng.QuadraticfinitevolumemethodforpricingAmericanoptions[J].MathematicNumericaSinica, 2015, 37(1): 67.

[14]GanXT,YinJF.Symmetricfinitevolumeelementapproximationsofsecondorderlinearhyperbolicintegro-differentialequations[J].ComputersandMathematicswithApplications, 2015, 70 (10): 2589.

[15]CryerCW.Thesolutionofaquadraticprogrammingusingsystematicoverrelaxation[J].SIAMJournalonControlandOptimization, 1971, 9(3): 385.

[16]IkonenS,ToivanenJ.OperatorsplittingmethodsforAmericanoptionpricingwithstochasticvolatility[J].NumerischeMathematik, 2009, 113(2): 299.

[17]张凯. 美式期权定价——基于罚方法的金融计算 [M]. 北京：经济科学出版社, 2012.

ZHANGKai.PricingAmericanoptions—financialcomputationbasedonthepenaltymethod[M].Beijing:EconomicSciencePress, 2012.

[18]MurtyK.Linearcomplementarity,linearandnonlinearprogramming[M].Berlin:Heldermann, 1988.

[19]HadjidimosA,TzoumasM.Nonstationaryextrapolatedmodulusalgorithmsforthesolutionofthelinearcomplementarityproblem[J].LinearAlgebraanditsApplications, 2009, 431(1): 197.

[20]DongJL,JiangMQ.Amodifiedmodulusmethodforsymmetricpositive-definitelinearcomplementarityproblems[J].NumericalLinearAlgebrawithApplications, 2009, 16(2): 129.

[21]BaiZZ.Modulus-basedmatrixsplittingiterationmethodsforlinearcomplementarityProblems[J].NumericalLinearAlgebrawithApplications, 2010, 17(6): 917.

[22]ZhengN,YinJF.Modulus-basedsuccessiveoverrelaxationmethodforpricingAmericanoptions[J].JournalofAppliedMathematicsandInformatics, 2013, 31(5): 769.

[23]ZhengN,YinJF.Acceleratedmodulus-basedmatrixsplittingiterationmethodsforlinearcomplementarityproblem[J].NumericalAlgorithms, 2013, 64(2): 245.

FiniteVolumeMethodsforPricingJump-DiffusionOptionModel

GANXiaoting1,2,YINJunfeng1,LIRui1,3

(1.DepartmentofMathematics,TongjiUniversity,Shanghai200092,China; 2.SchoolofMathematicsandStatistics,ChuxiongNormalUniversity,ChuxiongYunnan675000,China; 3.CollegeofMathematicsPhysicsandInformationEngineering,JiaxingUniversity,JiaxingZhejiang314001,China)

FinitevolumemethodsaredevelopedforpricingAmericanoptionsunderKoujump-diffusionmodel.Basedonalinearfiniteelementspace,bothbackwardEulerandCrank-Nicolsonfulldiscretefinitevolumeschemesareconstructed.Fortheapproximationoftheintegralterminthepartialintegro-differentialequation(PIDE),aneasy-to-implementrecursionformulaisemployed.Thenweproposethemodulus-basedsuccessiveoverrelaxation(MSOR)methodfortheresultinglinearcomplementarityproblems(LCPs).TheH+matrixpropertyofthesystemmatrixwhichguaranteestheconvergenceoftheMSORmethodisanalyzed.Numericalexperimentsconfirmtheefficiencyandrobustnessoftheproposedmethods.

finitevolumemethod;Koujump-diffusionoptionmodel;linearcomplementarityproblem;modulus-basedsuccessiveoverrelaxationmethod

2015-11-09

国家自然科学基金(11271289), 中央高校基本科研业务费专项资金, 云南省应用基础研究计划青年项目(2013FD045),云南省教育厅科学研究基金项目(2015Y443).

甘小艇(1983—), 男, 博士生, 主要研究方向为金融计算.E-mail: 9xtgan@tongji.edu.cn

殷俊锋(1979—), 男, 理学博士, 教授, 博士生导师, 主要研究方向为金融计算.E-mail:yinjf@tongji.edu.cn

O241.8

A