具有未知输入非线性系统的自适应观测器设计

朱芳来， 蒋　鹏， 李晓航

(同济大学 电子与信息工程学院，上海 201804)



具有未知输入非线性系统的自适应观测器设计

朱芳来， 蒋鹏， 李晓航

(同济大学 电子与信息工程学院，上海 201804)

针对具有未知输入和传感器噪声的的非线性系统，讨论了基于T-S(Takagi-Sugeno)模型的未知输入观测器设计方法.首先，给出了基于非线性系统构造T-S模型系数矩阵的计算方法.然后，以T-S模型作为设计模型，通过扩展传感器噪声为辅助状态向量的方式，将系统扩展为增维系统.继而，针对T-S模型，设计模糊自适应观测器以达到对非线性系统状态，未知输入和传感器噪声同时估计之目的.为此，基于线性矩阵不等式，给出了观测器存在的充分性条件.最后，通过实例仿真验证了此方法的有效性.

自适应观测器；T-S模型； 未知输入重构； 传感器噪声重构； 不可测前件变量

在实际的控制系统中，未知输入具有广义的含义，它可以是模型参数的不确定性，可以是系统所受到的外部干扰，也可以是系统的执行器故障信号等.基于这样的原因，未知输入观测器(unknowninputobservers,UIO)设计的研究，具有重要意义和很好的应用前景，如在容错控制、故障诊断与隔离和基于混沌同步的保密通讯等方面的应用，都有很好的应用，因而UIO设计成为控制领域所关注的热点问题之一[1-3].例如，文献[1]针对一类带有未知输入和相应延迟的线性系统，设计了未知输入观测器. 文献[2]对具有未知输入的线性系统，在观测器匹配条件不满足的情况下，设计了降维和高阶滑模观测器来估计系统的状态.文献[3]通过代数矩阵运算的方式，对线性变参数系统设计了未知输入观测器.

T-S模糊模型作为描述复杂非线性系统的有效手段之一，自提出以来，便得到国内外学者的广泛关注.T-S模型有着简单的动态结构，且能以任意的精度逼近任何一个光滑的非线性函数，这使得借用线性系统的设计方法来解决一些非线性问题就成为可能，由于这样的原因，基于T-S模糊模型的观测器设计，成为观测器设计领域中的研究热点之一[4-8].例如，文献[4]针对非线性动态系统，通过一步一步的将高阶滑模观测器扩展为T-S模糊模型方法，提出了一种传感器故障检测与隔离问题的解决方案.文献[5]对动态T-S模糊系统，分析和设计了两种不同的滑模观测器.文献[6]对具有未知多项式输入的T-S模糊系统，设计了自适应观测器来同时估计状态和未知输入.文献[7]研究了离散模糊观测器设计方法，提出了一种新的将非线性矩阵不等式(LMI)条件转化为LMI形式的解耦方法，并将其应用到主动容错控制中.文献[8]针对具有传感器故障的模糊随机系统，设计了鲁棒观测器进行故障估计，同时，基于观测器给出了模糊容错控制方案.值得注意的是，许多现有的工作是建立在可测量前件变量T-S(Takagi-Sugeno)模型的情况下完成的，然而在许多实际情况下，其前件变量是不可测的.目前，在基于T-S模型的观测器设计研究中，对于前件不可测的情况得到了广泛关注，并提出了一些成果[9-11].例如，文献[9]对具有不可测前件变量的T-S模糊系统，设计了未知输入比例积分观测器.文献[10]针对不可测前件变量的T-S模糊系统，采用广义冗余的方法，设计了鲁棒H∞跟踪器.文献[11]基于不可测前件变量设计了观测器，以达到故障诊断的目的.然而从目前已有的研究成果来看，文献[1-3,6]只考虑了未知输入的估计，文献[4,8,11]也只对故障进行诊断，而对同时具有未知输入和传感器故障的观测器设计尚未有报道.因而，基于前件为未知的T-S模型，讨论同时具有未知输入和传感器噪声的未知输入观测器设计，具有重大意义.

本文针对不可测前件变量的T-S模糊系统，在具有未知输入和传感器噪声的情况下，提出一种模糊自适应观测器设计方法来估计非线性系统的状态，同时还给出了未知输入和传感器噪声重构的方法.本文的主要创新点体现在：对不可测前件变量的模糊系统，设计了模糊自适应观测器，并提出了状态、未知输入和传感器噪声同时估计的方法.

1　T-S模型构造

考虑一类非线性系统模型如下：

(1)

其中,x∈Rn,y∈Rp,u∈Rm分别为状态、可测输出和控制输入向量；η∈Rr和ω∈Rw分别是未知输入和传感器噪声.函数φ为非线性项.B∈Rn×m，D∈Rn×r，C∈Rp×n和E∈Rp×w为相应维数的矩阵.假设矩阵D和E列满秩.

假设1:函数φ是连续可微的，φ(0)=0.

考虑T-S模糊模型如下：

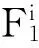
则:

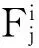
(2)

式中：Ai∈Rn×n，Bi∈Rn×m是第i个局部模型具有相应维数的矩阵，而

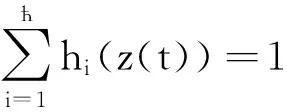
式(2)中具体参数矩阵可由文献[12]提出的方法得到，对任意状态x(j)，j=1,…,N，N是局部线性模型的个数，求出Aj和Bj，满足：

(3)

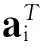
(4)

根据泰勒公式展开式(4)并忽略高阶项，则:

(5)

(6)

根据文献[13]给出的方法求解式(6)，则对x(j)≠0，有

定义Dφ(x(j))为φ在x=x(j)出的雅克比矩阵，非线性系统(1)可转化为

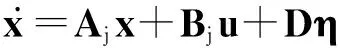
其中

(7)

命题1根据假设1，对于任意的εφ>0，存在带有模糊权值hi(·)的T-S模糊系统(2)，可近似地描述系统(1)，其近似误差为

证明因为矩阵B,C,D,E是常数矩阵，所以这是对文献[14]中证明的简单扩展.

引理1给定一个标量δ>0.对任意的向量α和β，有:

注1隶属度函数通常是非线性的，且依赖于前件变量的选取.对于系统而言，如果前件变量只包含{u(t),y(t)}，则前件变量是可测的；如果包含系统状态x(t)，则是不可测的.本文讨论的前件变量取为z(t)=x(t)，即前件变量是不可测的情形.

本文的主要目的，是以T-S模型(2)为设计模型，设计自适应观测器，来估计原非线性系统(1)的状态，同时给出未知输入和传感器噪声的重构方法.为后续阐述方便，在不引起歧义的情况下将变量进行简写，如Γ(t)写成Γ.

2　自适应观测器设计

(8)

如果系统(8)存在自适应观测器，就可以同时估计出x和ω.下面将设计一个自适应观测器来同时估计x，ω和η.

对于系统(8)，设计自适应观测器如下：

(9)

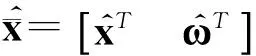
注2式(9)通过自适应调节律实现了未知输入η的在线跟踪，所以称式(9)所设计的观测器为自适应观测器.与文献[15]中的方法相比，本文式(9)中的第4个方程对未知输入的估计，只用到了输出误差的信息，而文献[15]，用到了输出误差的导数.

引理2存在两个矩阵G∈R(n+w)×n和F∈R(n+w)×p满足:

(10)

证明式(10)可等效为

(11)

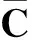
存在.于是式(11)存在关于矩阵G和F的解，它们的一个解为

(12)

所以误差动态系统可描述为

(13)

则误差方程可被描述为

(14)

此外，如果令Hi=Li+NiF，则式(13)可等效描述为

(15)

同理

(16)

注3故障可分为常数和缓时变故障.例如，在现实系统中，硬件突然遭到破坏或者出现大的偏差，就可以称之为常数故障；由于组件磨损和老化而导致的执行器性能的缓慢下降，可作为缓时变故障.因而，对于常数故障的检测和重构，具有重大意义.

根据假设3和式(9)的第4个方程，未知输入估计误差动态方程为

(17)

(18)

定理1针对系统(8)，对于给定的正的标量β和ε1，如果对正定矩阵P∈R(n+w+r)×(n+w+r)和矩阵Xi∈R(n+w+r)×p使如下的线性矩阵不等

(19)

通过引理1和假设2，且β>0，即可以得出：

所以

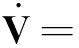
其中

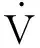
观测器(9)的未知矩阵Ni,Li,G,F和Φi的计算方法总结如下：

步骤1：通过式(12)计算出矩阵G和F.

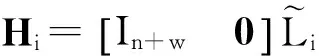
步骤4：通过式(15)和式(16)，计算出矩阵Ni，和Li.

3　仿真

考虑一个由直流电机驱动的倒立摆[16-17]，如图1所示.其基本控制输入方程为

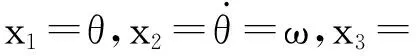
图1　倒立摆

通过文中第1部分提到的方法，系统可转化为局部线性系统，如下：

取两个平衡点为

则

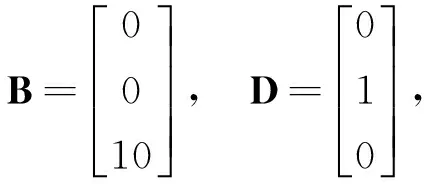
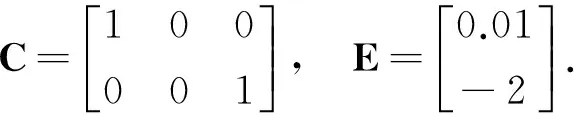
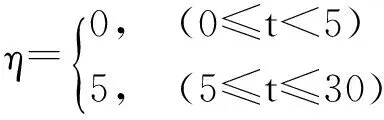
通过求解线性矩阵不等式(LMI)式(19)得到:

通过式(15)和式(16)可得：

根据设计的观测器得到系统的状态估计，如图2所示.由误差曲线图3可知，其是渐近收敛的.图4对传感器噪声进行了重构，图5则对未知输入进行了重构.由图2—5可知，系统的状态、传感器噪声和未知输入重构是令人满意的.

a x1

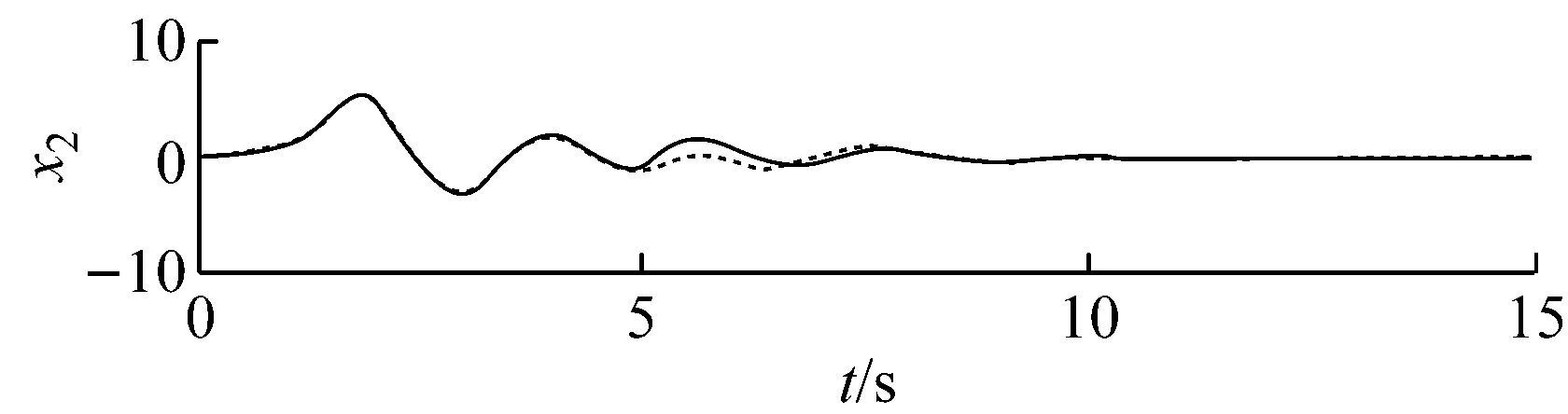
b x2

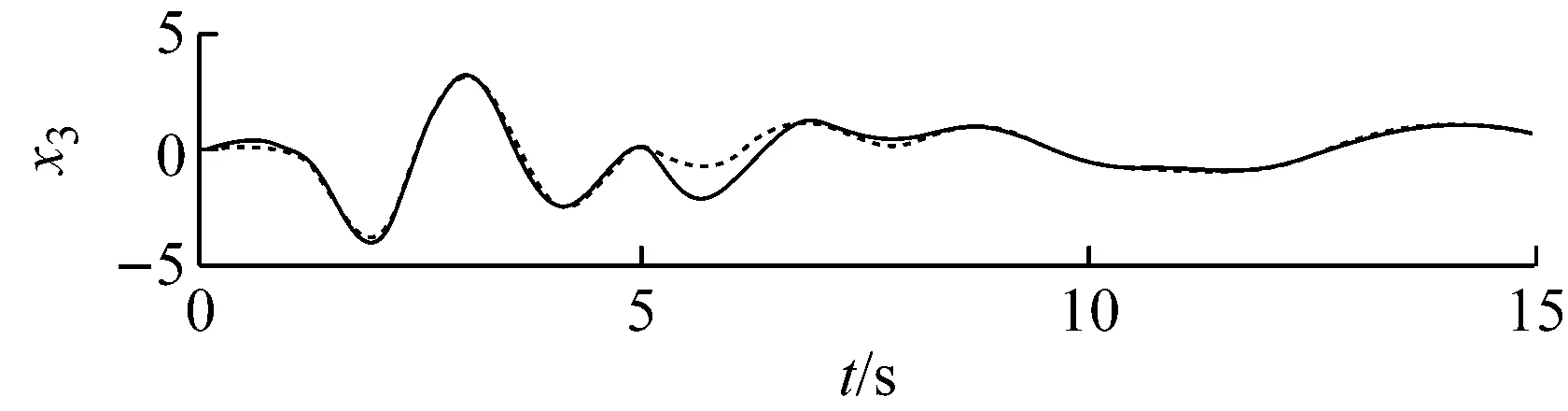
c x3

图2状态估计

Fig.2Stateestimation

a x1

b x2

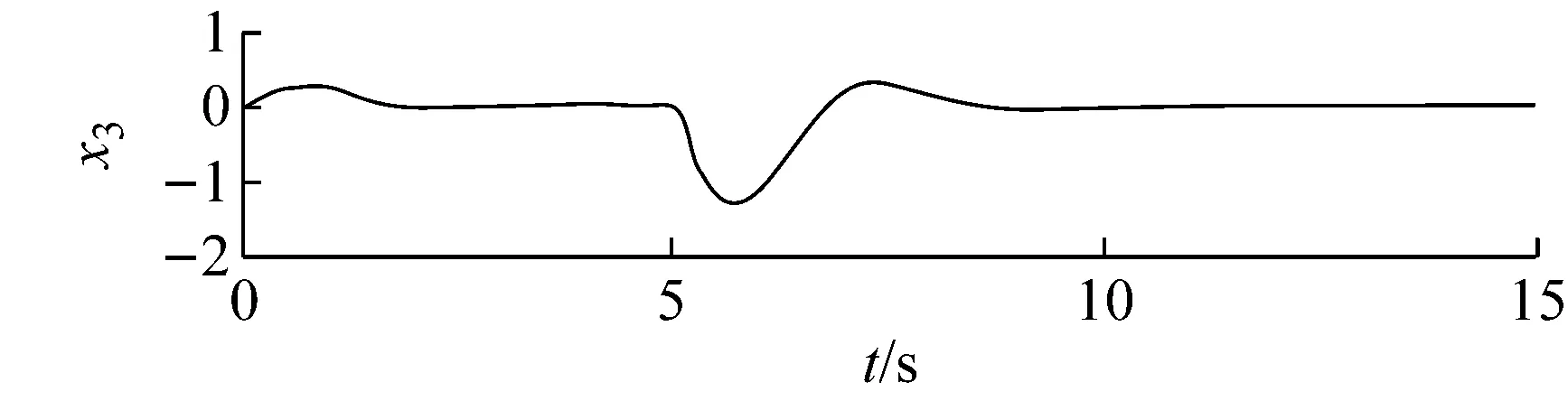
c x3

图4　传感器噪声重构Fig.4　Measurement noise reconstruction

图5　未知输入重构Fig.5　Unknown input reconstruction

4　结论

本文基于不可测前件变量的T-S模糊模型，对非线性系统提出了一种自适应未知输入观测器设计的方法，达到了对非线性系统状态，未知输入和传感器噪声同时估计之目的.通过线性矩阵不等式的方式，给出了观测器存在的充分性条件.仿真结果验证了所提出的方法对非线性系统的有效性.

[1]GangZ,FranciscoJB,WilfridP, et al.Unknowninputobserverforlineartime-delaysystems[J].Automatica, 2015,61: 35.

[2]ZhuF.Stateestimationandunknowninputreconstructionviabothreduced-orderandhighorderslidingmodeobservers[J].JournalofProcessControl,2012,22(1): 296.

[3]IchalalD.OnUnknownInputObserversforLPVSystems[J].IEEETransactionsonIndustrialElectronics,2015,62(9): 5870.

[4]HaouariFA,DjemaiM,CherkiB.SlidingmodeobserversforT-Sfuzzysystemswithapplicationtosensorfaultestimation[C]∥Control,Engineering&InformationTechnology, 2015 3rdInternationalConferenceon.Tlemcen:IEEE,2015：1-5 .

[5]BergstenP,PalmR,DriankovD.ObserversforTakagi-Sugenofuzzysystems[J].Systems,Man,andCybernetics,PartB:Cybernetics,IEEETransactionson,2002, 32(1): 114.

[6]LendekaZ,LauberbJ,GuerraTM.AdaptiveobserversforTSfuzzysystemswithunknownpolynomialinputs[J].FuzzySetsandSystems,2010,161(15)：2043.

[7]TsengCS,ChenBS,LiYF.Robustfuzzyobserver-basedfuzzycontroldesignfornonlinearsystemswithpersistentboundeddisturbances:anoveldecoupledapproach[J].FuzzySetsandSystems,2009, 160(19): 2824.

[8]LiuM,CaoX,ShiP.Faultestimationandtolerantcontrolforfuzzystochasticsystems[J].FuzzySystems,IEEETransactionson,2013, 21(2): 221.

[9]YoussefbT,ChadliaM,KarimiHR.DesignofunknowninputsproportionalintegralobserversforTSfuzzymodels[J].Neurocomputing,2014,123(10):156.

[10]AsemaniMH,MajdVJ.ArobustH-infinity-trackingdesignforuncertainTakagi-Sugenofuzzysystemswithunknownpremisevariablesusingdescriptorredundancyapproach[J].InternationalJournalofSystemsScience,2015,46(16): 2955.

[11]GhorbelH,SouissiM,ChaabaneM, et al.Observerdesignforfaultdiagnosisforthetakagi-sugenomodelwithunmeasurablepremisevariables[C]∥Control&Automation(MED), 2012 20thMediterraneanConferenceon.Barcelona:IEEE,2012:303-308.

[12]TeixeiraM,ZakS.Stabilizingcontrollerdesignforuncertainnonlinearsystemsusingfuzzymodels[J].IEEETransactionsonFuzzySystems,1999,7(2) 133.

[13]ChongE,ZakS.AnIntroductiontoOptimization[M]. 4thed.Beijing:JohnWiley&Sons, 2013.

[14]GaoQ,ZengX,FengG, et al.T-S-fuzzy-model-basedapproximationandcontrollerdesignforgeneralnonlinearsystems[J].IEEETransactionsonSystems,2012,42(4): 1143.

[15]ZhangJ,SwainAK,NguangSK.RobustH∞adaptivedescriptorobserverdesignforfaultestimationofuncertainnonlinearsystems[J].JournaloftheFranklinInstitute,2014, 351(11): 5162.

[16]KawamotoS.Nonlinearcontrolandrigorousstabilityanalysisbasedonfuzzysystemforinvertedpendulum[C]∥FuzzySystems, 1996,ProceedingsoftheFifthIEEEInternationalConferenceon.Neworleans:IEEE,1996: 1427-1432.

[17]KazuoT,TakayukiL,HuaOW.Fuzzyregulatorsandfuzzyobservers:relaxedstabilityconditionsandLMI-baseddesigns[J].IEEETransactionsonFuzzySystems, 1998,6(2): 250.

AdaptiveObserverDesignwithUnknownInputsforNonlinearSystems

ZHUFanglai,JIANGPeng,LIXiaohang

(1.SchoolofElectronicsandInformationEngineering,TongJiUniversity,Shanghai201804,China)

Forthenonlinearsystemswithunknowninputsandmeasurablenoises,thedesignmethodofunknowninputobserverbasedontheT-Smodelisdiscussed.Atfirst,thecalculationmethodofthecoefficientmatrixoftheT-Smodelconstructedbasedonnonlinearsystemispresented.Then,theT-Smodelisusedasthedesignmodel,andthesystemisextendedtoanaugmentedsystembyextendingthemeasurablenoiseasanauxiliarystate.Andthen,fortheT-Smodel,afuzzyadaptiveobserverisdesignedtoachievetheobjectiveofthesimultaneousestimationsofthestates,theunknowninputsandthemeasurablenoisesofthenonlinearsystem.Meanwhile,thesufficientconditionoftheexistenceoftheobserverisgivenbasedonalinearmatrixinequality.Finally,simulationexamplesdemonstratetheeffectivenessofthismethod.

adaptiveobserver;T-Smodel;unknowninputreconstruction;measurementnoisereconstruction;unmeasuredpremisevariables

2015-10-29

国家自然科学基金(61074009).

朱芳来(1965—)，男，教授，工学博士，博士生导师；主要研究方向为观测器设计，故障诊断与容错控制等.

E-mail:zhufanglai@tongji.edu.cn

TH317

A