挡土墙地震土压力的拟动力分析

王　浩， 董建华， 王永胜， 张　媛

(1．兰州理工大学 甘肃省土木工程防灾减灾重点实验室，兰州　730050；2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州　730050)



挡土墙地震土压力的拟动力分析

王浩1，2， 董建华1,2， 王永胜1,2， 张媛1,2

(1．兰州理工大学 甘肃省土木工程防灾减灾重点实验室，兰州730050；2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州730050)

基于均匀土层剪切梁理论建立了边坡水平地震动力运动方程，得到了边坡坡后土体的水平位移和加速度响应。将水平加速度应用到挡土墙地震土压力拟动力分析中，对坡体刚性假定和加速度沿坡高恒定的不足进行了改进，推导出主动、被动土压力的计算公式。结合实际工程分析了墙后填土面倾角、填土内摩擦角、挡墙与填土界面摩擦角对于总土压力大小的影响，并与传统的拟静力法和拟动力法进行了比较，结果表明：地震土压力随着时间呈一种类似正弦或者余弦状波动；随着墙后填土面倾角增大挡土墙地震总主、被土压力的也呈逐渐上升趋势；随填土内摩擦角、以及挡土墙与填土界面摩擦角的增大挡土墙地震总主动土压力逐渐减小，而被动土压力则随之增大;传统的计算方法由于计算值偏小而不安全。

剪切梁理论；拟动力分析；挡土墙；地震土压力；地震系数

近年来，世界各地频繁的地震灾害对人民的生命财产造成了巨大损失，其中交通生命线的破坏更是给抗震救灾工作造成了极大困难。挡土墙作为一种最常见的支护结构在公路、铁路等边坡工程中应用比较普遍[1]，地震时一旦发生破坏将严重阻碍道路的畅通，同时会危及人们的生命安全，因此挡土墙的抗震设计尤为重要。国内外很多学者对于挡土墙的抗震设计进行了大量研究，最早提出的是Mononobe-Okabe理论，也称之为拟静力法，它是一种用静力原理近似解决动力学问题的简易方法。 张建民[2]等以Mononobe-Okabe理论为基础，给出了考虑填土侧向变形的挡土墙地震土压力分析方法；宋飞[3]等基于拟静力法和曲面中间滑楔体的概念进行了地震动土压力分析；刘忠玉等[4]利用水平层分析法对平移模式下挡土墙的地震土压力进行了分析；文畅平[5]利用拟静力法和塑性极限分析上限定理，对于多级组合支挡结构的地震土压力进行了研究；陆新[6]等对于目前各规范中提出的地震荷载作用下边坡土压力的计算公式的工程适用性和公式差别进行了分析。

拟静力学方法虽然计算简便，但是没有考虑地震时间及相位差的影响，而且许多假设条件与实际情况存在很大差异，例如将坡体假定为刚性体。为了弥补以上缺点，剑桥大学的ZENG等[7]提出了拟动力方法，假设随时间与深度地震加速度的大小形如正弦曲线式变化，且切变模量在滑移面范围内为有限定值。CHOUDHURY等[8]采用拟动力法对重力式挡土墙被动状态下的被动土压力作了初步研究。刘礼标等[9]提出了采用离散化剪切梁的分析模型，对于墙后土层为非均质时刚性挡土墙的地震土压力进行了研究，并分析了不同剪切模量情况下土压力的变化，合力增量以及合力作用点等受到的影响。阮晓波等[10-11]采用拟动力分析法，基于滑动楔体极限平衡理论，得出了地震作用下挡土墙主动、被动土压力的计算公式以及破裂角的大小，并分析了挡土墙后填土的内摩擦角、挡土墙与填土之间的摩擦角、挡土墙的倾角以及超载角等参数对最危险滑移面位置和地震主动土压力的影响。王志凯等[12]基于拟动力分析法的基本假定同时考虑地震加速度的放大效应，利用水平层分析法求解了挡土墙地震主动土压力的大小并分析了最危险滑移面的位置，最后探讨了水平加速度系数及加速度放大系数对于地震土压力强度分布的影响。杨长卫等[13]提出地震作用下刚性挡土墙地震主动土压力的时频域计算方法，分析了输入波频率对刚性挡土墙墙后填土的临界破裂角、地震主动土压力合力以及作用点的影响。

以上学者利用拟静力法或者拟动力法对挡土墙地震土压力做了大量研究工作，但其中对于地震加速度的描述过于单一，获得的地震土压力实质上是对静土压力的一种简单放大，无法考虑持时和频率对土压力的影响，与实际明显不相符，为了得到更精确的地震加速度，本文基于均匀土层剪切梁理论，在文献[14]建立的边坡水平地震动力运动方程的基础上，求解了地震水平加速度，改进了挡土墙地震土压力拟动力分析方法，得到了主动、被动土压力计算公式，结合实际工程分析了墙后填土面倾角β、填土内摩擦角φ、挡墙与填土界面摩擦角δ等参数对总土压力的影响。得到了一些对挡墙抗震设计具有指导性的结论。

1　地震水平加速度

对于高度为H的边坡，在坡体内取单位横截面土体为研究对象，t时刻z高度处的动位移响应为：

(1)

(2)

sin[ωd(t-τ)]dτ

(3)

式中：Dn为第n振型的阻尼比；ωn为第n振型的固有圆频率；M为震级；G为剪切模量；Ts为地震运动卓越周期；c为土体阻尼系数；ρ为土体密度。

将式(2)，式(3)代入式(1)中，便可求得地震水平加速度：

(4)

则有：

(5)

式中：

Mn=

2　挡土墙地震土压力理论计算

2.1基本假定

1) 挡土墙为刚性的。

2) 墙后回填土选用均质无黏性土。

3) 填土剪切模量G保持不变。

4) 水平地震加速度随时间和深度变化，且不考虑竖向地震加速度的影响。

2.2主动土压力计算

建立挡土墙计算模型(见图1)，挡土墙墙高H，墙后填土为均质无黏性土，外力作用下挡土墙发生平移，墙后填土达到极限平衡且形成了滑动楔体ABC。填土内摩擦角为φ、墙土间摩擦角为δ、土楔与水平面的破裂角为θ，墙后填土面倾角为β。

对滑动楔体ABC进行受力分析，作用力有：

1) 滑动楔体的重力Ws；

Ws=γsSΔABC

(6)

2) 滑裂面BC上的反力R；

3) 墙背AB上的主动土压力Pae；

4) 水平向地震惯性力Qh；因为不考虑竖向地震加速度影响，所以Qv=0。

图1　主动土压力计算模型Fig.1　The calculation model of active earth pressure

(7)

取z处一薄层单元为研究对象，厚度为dz，当dz足够小时，薄层单元可看作为一平行四边形。

薄层重度：

(8)

滑动楔体总重：

(9)

作用在整个破坏土楔上的总水平惯性力Qh(t)为：

(10)

将式(5)代入上式积分可得：

(11)

对于滑块楔体ABC进行受力分析：

水平方向：

Paecosδ-Qh(t)=Rsin(θ-φ)

(12)

竖直方向：

Paesinδ-Ws=-Rcos(θ-φ)

(13)

解上式可得地震总主动土压力Pae：

(14)

2.3被动土压力计算

建立挡土墙计算模型(见图2)，挡土墙墙高H，墙后填土为均质无黏性土，外力作用下挡土墙发生平移，墙后填土达到极限平衡且形成了滑动楔体ABC。填土内摩擦角为φ、墙土间摩擦角为δ、土楔与水平面的破裂角为θ，墙后填土面倾角为β。

对滑动楔体ABC进行受力分析，作用力有：

1) 滑动楔体的重力Ws；

Ws=γsSΔABC

(15)

2) 滑裂面BC上的反力R；

3) 墙背AB上的被动土压力Ppe；

4)水平向地震惯性力Qh；因为不考虑竖向地震加速度影响，所以Qv=0。

图2　被动土压力计算模型Fig.2　The calculation model of passive earth pressure

式中：

(16)

薄层高度：

(17)

薄层重度：

(18)

滑动楔体总重：

(19)

作用在整个破坏土楔上的总水平惯性力Qh(t)为：

(20)

将式(17)代入上式积分可得：

(21)

对于滑块楔体ABC进行受力分析：

水平方向：

Ppecosδ+Qh(t)=Rsin(θ+φ)

(22)

竖直方向：

Ppesinδ+Ws=Rcos(θ+φ)

(23)

解上式可得地震总被动土压力Ppe如下：

(24)

将式(14)和式(23)对H求导可得地震土压力沿坡高的分布

(25)

3　算例分析

甘肃兰州某地区高速公路边坡高度为10 m,场地类型为Ⅱ类。查阅相关规范兰州地区的抗震设防烈度取8度，根据烈度与地震加速度峰值对照表amax取0.2 g，因为场地类型为Ⅱ类，故取卓越周期Ts=0.5 s，土体剪切模量G=7.7 MPa。土体天然重度为γ=18 kN/m3，输入地震波为正弦波，持续时间为10 s。

3.1主动土压力分析

地震总主动土压力在不同的填土摩擦角φ的情况下，随地震波持续10 s内的主动土压力的变化情况(见图3)。

图3　主动土压力随t值变化曲线Fig.3　Curves of the active earth pressure with t

从图3可知，地震总主动土压力在地震初始阶段出现大幅度的波动，呈现出类似正余弦的变化规律，在经历大约6 s的时间后，土压力的大小逐渐趋于平稳，这主要是由于阻尼存在的原因；并且在墙后填土面倾角β=0°，墙土摩擦角δ=1/2φ保持不变时，在相同时间的情况下，填土内摩擦角φ=10°的地震主动土压力大于φ=15°时，即地震主动土压力随填土内摩擦角φ的增大而减小。

地震总主动土压力在不同的墙土摩擦角δ的情况下，随地震波持续10 s内的主动土压力的变化情况(见图4)。

图4　不同δ情况下主动土压力随t值变化曲线Fig.4　Curves of the active earth pressure with t under different δ

从图4中除了可知图3的结论外，还可知在墙后填土面倾角β=5°恒定不变的情况下，墙土摩擦角δ从1/3φ增加到2/3φ时，地震总主动土压力会有相似幅度的减小；并通过图3与图4的对比可知在φ值、δ值、t值均相同的情况下，地震总主动土压力随着β值的增大而增大。

地震总主动土压力在地震震动初期不同时刻，随填土内摩擦角φ的变化地震总主动土压力的变化情况(见图5)。

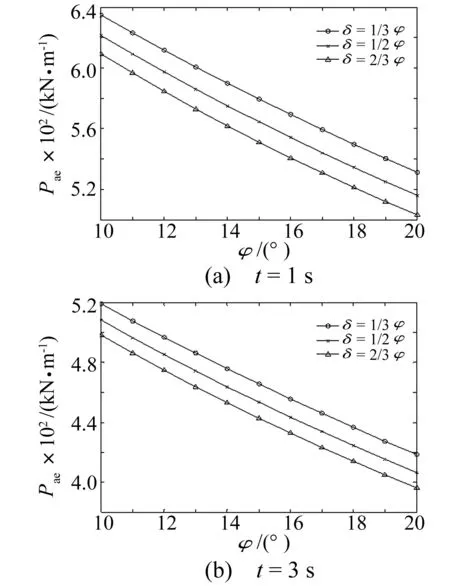
图5　不同δ情况下主动土压力随φ值变化曲线Fig.5　Curves of the active earth pressure with φ under different δ

从图5(a)和图5(b)可知，t=1 s的地震总主动土压力大于t=3 s时的土压力；在墙后填土面倾角β保持不变的情况下，地震总主动土压力随着填土内摩擦角φ、墙土摩擦角δ的增大而减小。

取填土内摩擦角φ=10°，墙土摩擦角δ=1/2φ，墙后填土面倾角β=0°，破裂角θ=1/2φ+45°，对比相同条件下用本文方法、传统拟动力法及传统拟静力法求得的挡土墙地震主动土压力沿墙高的分布(见图6)。

图6　不同计算方法下的主动土压力对比Fig.6　Comparison of the active earth pressure for different calculation methods

从图6可知，文中方法地震主动土压力随墙高逐渐增大，在坡下部小于拟动力法和拟静力法计算值，而在坡体上部大于，并且文中的方法在相同条件下得到的地震主动土压力最大，传统拟动力法次之，传统拟静力法最小，说明文中方法解决了传统方法计算得到的土压力值偏小这个问题，得到的土压力分布值更接近于实际的分布规律。文献[15]中通过谐振定律得到地震土压力分布为倒三角形或上大下小的抛物线分布，与本文得到的分布类似，而传统的拟动力法和拟静力法都是在静土压力分布的基础进行的一种简单的放大，与实际出入比较大。事实上，通过分析可知，对于一个土坡，地震时坡脚处位移为零，沿坡高逐渐增大，最大位移发生在坡体的顶部，从而可得加速度沿坡高是放大的。滑动楔体的质量分布也沿坡高增大，因此，如果挡土结构限制坡后土体时，坡体位移大的部位动土压力就大，坡体位移小的部位，动土压力就小，从而可得动土压力沿墙高分布是逐渐放大的。在坡顶附近幅值增量减小，这主要是坡面角度的影响造成的，如果坡角到达90°，则坡顶附近幅值增量最大。

3.2被动土压力分析

地震总被动土压力在不同的填土摩擦角φ的情况下，随地震波持续10 s内的被动土压力的变化情况(见图7)。

图7　不同β情况下被动土压力随t值变化曲线Fig.7　Curves of the passive earth pressure with t under different β

从图7可知，地震总被动土压力变化和衰减规律与主动土压力相似；在墙土摩擦角δ恒定时，地震总被动土压力随填土内摩擦角φ、墙后填土面倾角β的增大而增大。

地震总被动土压力在地震震动初期不同时刻，随填土内摩擦角φ的变化地震总被动土压力的变化情况(见图8)。

图8　不同δ情况下被动土压力随φ值变化曲线Fig.8　Curves of the passive earth pressure with φ under different δ

从图8(a)和图8(b)可知，在墙后填土面倾角β保持不变的情况下，地震总被动土压力随着填土内摩擦角φ、墙土摩擦角δ的增大而增大。

取填土内摩擦角φ=10°，墙土摩擦角δ=1/2φ，墙后填土面倾角β=0°，破裂角θ=1/2φ+45°，对比相同条件下用本文方法、传统拟动力法及传统拟静力法求得的挡土墙地震被动土压力沿墙高的分布(见图9)。其规律和分布与前述主动土压力类似，而坡顶部土压力峰值增量受坡角影响更加明显。

图9　不同计算方法下的被动土压力对比 Fig.9　Comparison of the passive earth pressure for different calculation methods

4　结　论

(1) 利用边坡半无限土体水平地震动力方程求解得到了水平地震加速的计算公式，对地震土压力计算的拟动力法进行了改进。该方法考虑了加速度沿坡高放大效应、地震动频率和持时对动土压力的影响。

(2) 通过分析可知，地震总主、被动土压力在地震初始阶段出现大幅度的变化，随着地震时间的持续逐渐归于平稳，呈类似余弦或正弦曲线式变化。

(3) 在其它条件保持不变的情况下，地震总主、被动土压力随着墙后填土面倾角β值的增大而增大；地震总主动土压力随着填土内摩擦角φ、墙土摩擦角δ的增大而减小；地震总被动土压力随着填土内摩擦角φ、墙土摩擦角δ的增大而增大。

(4) 土压力分布为非线性，呈上下小、中间大的枣核形状。相同条件下，本文改进的方法计算的地震主、被动土压力最大，传统拟动力法次之，传统拟静力法最小，说明得到的土压力分布值更接近于实际的分布规律。

[1] 王洪亮, 宋二祥, 宋福渊. 紧邻既有建筑基坑有限土体主动土压力计算方法[J]. 工程力学, 2014, 31(4):76-81.

WANG Hongliang, SONG Erxiang, SONG Fuyuan. Calculation of active earth pressure for limited soil between existing building and excavation[J]. Engineering Mechanics, 2014, 31(4):76-81.

[2] 张建民, 宋飞. 考虑填土侧向变形的地震土压力计算方法[J]. 地震工程学报, 2013, 35(1):9-20.

ZHANG Jianmin,SONG Fei. Evaluation of seismic earth pressure considering later deformation[J]. China Journal of Earthquake Engineering, 2013,35(1):9-20.

[3] 宋飞, 张建民, 陈友昆. 地震荷载作用下被动侧向土压力计算方法研究[J].世界地震工程,2010,26(增刊1):335-340.

SONG Fei, ZHANG Jianmin,CHEN Youkun.Study on calculation methods of earth pressures at the passive side under seismic loads[J].World Earthquake Engineering, 2010,26(Sup1):335-340.

[4] 刘忠玉, 杨会朋.刚性挡土墙地震主动土压力的非线性分布[J].郑州大学学报(工学版), 2004,25(2):36-38.

LIU Zhongyu,YANG Huipeng.Nonlinear distribution of seismic active earth pressure on rigid retaining walls[J].Journal of Zhengzhou University(Engineering Science),2004,25(2):36-38.

[5] 文畅平. 多级支挡结构地震主动土压力的极限分析[J].岩土力学,2013,34(11):3025-3212.

WEN Changping Limit analysis of seismic active earth pressure of multistage retaining structures[J].Rock and Soil Mechanics, 2013,34(11):3025-3212.

[6] 陆新, 胡源, 郑颖人. 关于地震主动土压力计算公式的讨论[J].建筑科学,2013,29(1)：58-61.

LU Xin,HU Yuan,ZHENG Yingren.Discussion on calculation formual of seismic active earth pressure[J].Building Science,2013,29(1)：58-61.

[7] ZENG X, STEEDOM R S . On the behaviour of quary walls in earthquakes[J].Gotechnique ,1993,43(3):417-431.

[8] CHOUDHURY D, NIMBALKAR S. Seismic passive resistance by pseudo-dynamic method[J]. Geotechnique, 2005, 55( 9) : 699-702.

[9] 刘礼标, 张永兴. 非均质填土刚性挡土墙的地震土压力分析[J].江苏大学学报,2013,34(3)：351-355.

LIU Libiao,ZHANG Yongxing.Analysis of seismic earth pressure for rigid retaining wall with inhomogeneous backfilled soil[J]. Journal of Jiangsu University,2013,34(3):351-355.

[10] 阮晓波, 孙树林. 基于拟动力方法的地震条件下挡土墙主动土压力研究[J].公路交通科技,2012,29(8)：26-30.

RUAN Xiaobo,SUN Shulin.Analysis of seismic active earth pressure on retaining wall based on pseudo-dynamic method[J].Journal of Highway and Transportation Research and Development,2012,29(8)：26-30.

[11] 杨剑. 挡土墙地震被动土压力的拟动力分析[J].防震减灾工程学报,2012,32(6):365-371.

YANG Jian. Study on passive earth pressure of vertical retaining walls by pseudo-dynamic analysis[J]. Journal of Disaster Prevention and Mitigation Engineering,2012,32(6):365-371.

[12] 王志凯, 夏唐代. 刚想挡土墙地震主动土压力的拟动力分析[J]. 浙江大学学报,2012,46(1):46-50.

WANG Zhikai,XIA Tangdai.Pseudo-dynamic analysis for seismic active earth pressure behind rigid retaining wall[J].Journal of Zhejiang University, 2012,46(1):46-50.

[13] 杨长卫, 张建经, 付晓, 等. SV 波作用下刚性挡土墙地震主动土压力时频域计算方法[J]. 岩石力学与工程学报, 2014, 33(3): 615-622.

YANG Changwei, ZHANG Jianjing, FU Xiao,et al.Time-frequency computational method of seismic active earth pressure of rigid retaining wall subjected to SV wave[J]. Chinese Journal of Rock Mechanics and Engineering，2014, 33(3): 615-622.

[14] 董建华, 朱彦鹏. 土钉边坡支护结构动力计算方法研[J].振动与冲击, 2011,30(2)：218-221.

DONG Jianhua,ZHU Yanpeng.Dynamic calculation method for soilnailing supporting structure[J]. Journal of Vibration and Shock,2011,30(2)：218-221.

[15] 顾慰慈. 挡土墙土压力计算[M]. 北京：中国建材工业出版社, 2001.

Pseudo-dynamic analysis on seismic earth pressure of retaining wall

WANG Hao1,2, DONG Jianhua1,2, WANG Yongsheng1,2, ZHANG Yuan1,2

(1. School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. Western Engineering Research Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China)

Based on the shear beam theory of homogeneous soil layer, the motion equation of the soil slope was established under the horizontal earthquake, and the horizontal displacement and acceleration response of the slope were solved. The defects of the assumptions of rigid slope and constant acceleration along the slope hight were improved by using the pseudo-dynamic method in the analysis and the horizontal acceleration solved in the calculation of seismic earth pressure. Then the formulas for calculating the active and passive earth pressure were derived. Considering the situations in practical engineering, the influences of the angle of filling soil behind retaining wall, the internal friction angle, and the interfacce friction angle between retaining wall and filling soil on the total earth pressure were analyzed and the improved method was compared with the traditional ones. The results show that the seismic earth pressure is like a sine or cosine wave in time domain. The seismic active and passive earth pressures increase with the increase of the angle of filling soil behind retaining wall. The total seismic active earth pressure decreases with the increase of internal friction angle and filling interface friction angle gradually, while the total passive earth pressure increases. The traditional methods are not safe due to that their results are usually inclined to the small side.

shear beam theory; pseudo- dynamic method; remaining wall; earth pressure; seismic coefficient

国家自然科学基金资助项目(51268037;51108221)；甘肃省杰出青年基金项目(145RJDA330)；陇原青年创新人才扶持计划(LYRC2014002)；兰州理工大学红柳杰青基金项目(J201403)；国家留学基金资助项目(2011862535)

2015-04-21修改稿收到日期：2015-08-27

王浩 男，硕士生，1990年生

董建华 男，博士，教授，博士生导师，1980年生

TU476

A DOI:10.13465/j.cnki.jvs.2016.14.021