屋盖开孔建筑的内压风洞试验研究

李寿科， 田玉基, 李寿英， 陈政清， 孙洪鑫

(1.湖南科技大学 土木工程学院，湖南 湘潭　411201; 2.北京交通大学 结构风工程与城市风环境北京市重点实验室,北京　100044;3.湖南大学 风工程与桥梁工程湖南省重点实验室，长沙　410082)



屋盖开孔建筑的内压风洞试验研究

李寿科1， 田玉基2, 李寿英3， 陈政清3， 孙洪鑫1

(1.湖南科技大学 土木工程学院，湖南 湘潭411201; 2.北京交通大学 结构风工程与城市风环境北京市重点实验室,北京100044;3.湖南大学 风工程与桥梁工程湖南省重点实验室，长沙410082)

对不同开孔位置、开孔率和内部容积的17个屋盖开孔建筑进行了缩尺刚性模型测压试验，分析内外风压的空间分布规律和相关性，采用稳态方法和单开孔内压传递方程分别对平均和脉动内压进行理论估计，拟合了峰值内外压系数比的无量纲设计公式。结果表明：屋盖开孔建筑的内部风压系数相关性和相干性较好，可采用统一的值来描述内压；内外风压系数以正相关为主，相关性大于立墙开孔工况；平均内压设计值可取为0.8倍开孔处外部平均风压，可采用单开孔内压传递方程估计垂直风向的脉动内压，误差小于15%。拟合的脉动内外压系数比和峰值内外压系数比设计公式，可应用于屋盖中心开孔建筑，改进了GINGER方法的精度。

风洞试验；屋盖开孔；相关系数；峰值内压

建筑的开孔通常可分为功能性开孔和破坏性开孔两类。功能性开孔按照开孔位置区分有立墙开孔和屋盖开孔，如立墙的门窗开孔，屋盖的功能性天窗、体育场的开合式屋盖。破坏性开孔是由建筑物的损坏而形成的一类开孔，可能发生在建筑的任何部位。对于低矮建筑，风致破坏性开孔通常较早的出现于屋盖的边缘或角部。屋盖表面开孔后，其风荷载不再完全由外表面风荷载决定，内部风荷载对结构净风荷载的贡献明显增大。目前国内外对于开孔结构风效应的研究大多集中于立墙开孔建筑，如HOLMES[1]对一立墙单开孔的双坡低矮房屋进行了风洞试验，采用了单参数的Helmohotz共振方程表示内压响应；随后，LIU等[2-4]对内压传递方程的开孔阻尼参数和损失参数的表达形式进行了进一步的推导和改进，得到了双参数或三参数的内压传递方程。余世策[5]通过刚性模型风洞试验研究了立墙开孔的建筑的内部风效应，对内压进行了理论估计。HOLMES等[6]对TTU(Texas Tech University Building Model)实测内压数据进行分析，拟合了脉动内外压之比设计公式。SHARMA等[7]对1∶50的立墙开孔TTU建筑进行风洞试验，研究了屋盖上下表面风压之间的相关性以及表面净风压分布规律。樊友川[8]对一系列不同高跨比的立墙开孔工业厂房进行了风洞试验，拟合了内风压系数随结构几何参数变化的设计公式。余先锋等[9-10]对立墙多开孔的单腔和双腔建筑的内压进行了理论与试验研究。

在实际工程中，功能性、破坏性的屋盖开孔建筑广泛存在。本文以屋盖顶部中心开孔和角部开孔的TTU建筑为研究对象，设置不同开孔率、不同开孔位置和不同内部容积共17种工况，研究建筑内部风压的空间分布特性，内外风压的相关特性，以及内风压的估计方法，对试验的峰值内外压比进行关于无量纲开孔参数和湍流度参数的公式拟合，得到的结果可用于指导工程设计。

1　刚性模型测压风洞试验概况

试验在湖南大学HD-2风洞的高速试验段进行。试验模拟了“建筑结构荷载规范:GB 50009—2012”中的B类地貌，风场比例为1∶50，平均风剖面指数为0.15，湍流度剖面也与实际大气中的情况基本一致，10 m高度处湍流度大小为0.20。试验模型采用有机玻璃制作，在主要尺寸上与TTU建筑(13.72 m×9.14 m×3.96 m)保持几何相似，在建筑屋盖的中心或角部进行不同比例的开孔，模型的几何缩尺比为1∶50，试验照片见图1。试验定义开孔面积与屋盖面积之比为开孔率。不同开孔率的屋盖开孔建筑的立墙测点布置相同，内外表面各56个测点，测点位置对应；屋盖测点数有所区别，上下表面测点位置对应，详细测点布置见图2。需注意的是，为了保证开孔结构内部脉动风压相似，需对结构内部体积进行扩充。

试验包括3种屋盖中心开孔(15%、20%、25%)，3种角部开孔(3%、5%、8%)，3种模型内部容积(9.00L3、7.29L3、5.76L3)，共计17种工况见表1，L表示原型尺寸。试验风向角定义见图2，风向角间隔5°，每个工况共测试72个风向角。采样时长33 s，采样频率330 Hz，共采集10 000个数据点。试验风速11.0 m/s，风洞中参考高度为8 cm。风洞试验数据处理方法详见文献[11]。

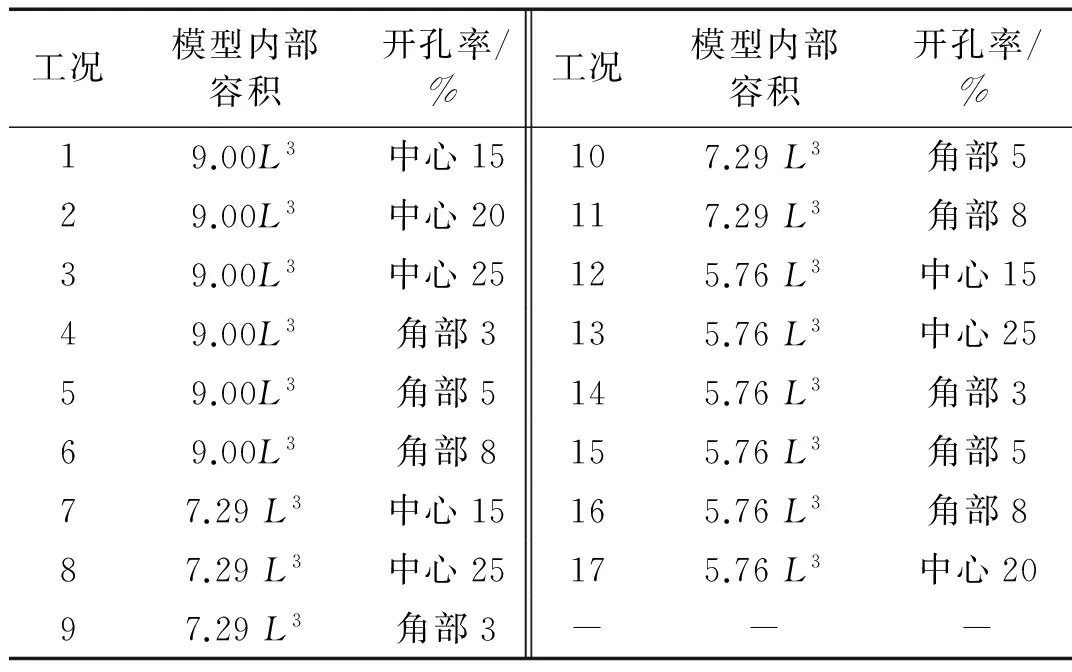
表1　屋盖开孔建筑风致内压试验工况

图1　试验模型照片Fig.1　Photo of test model

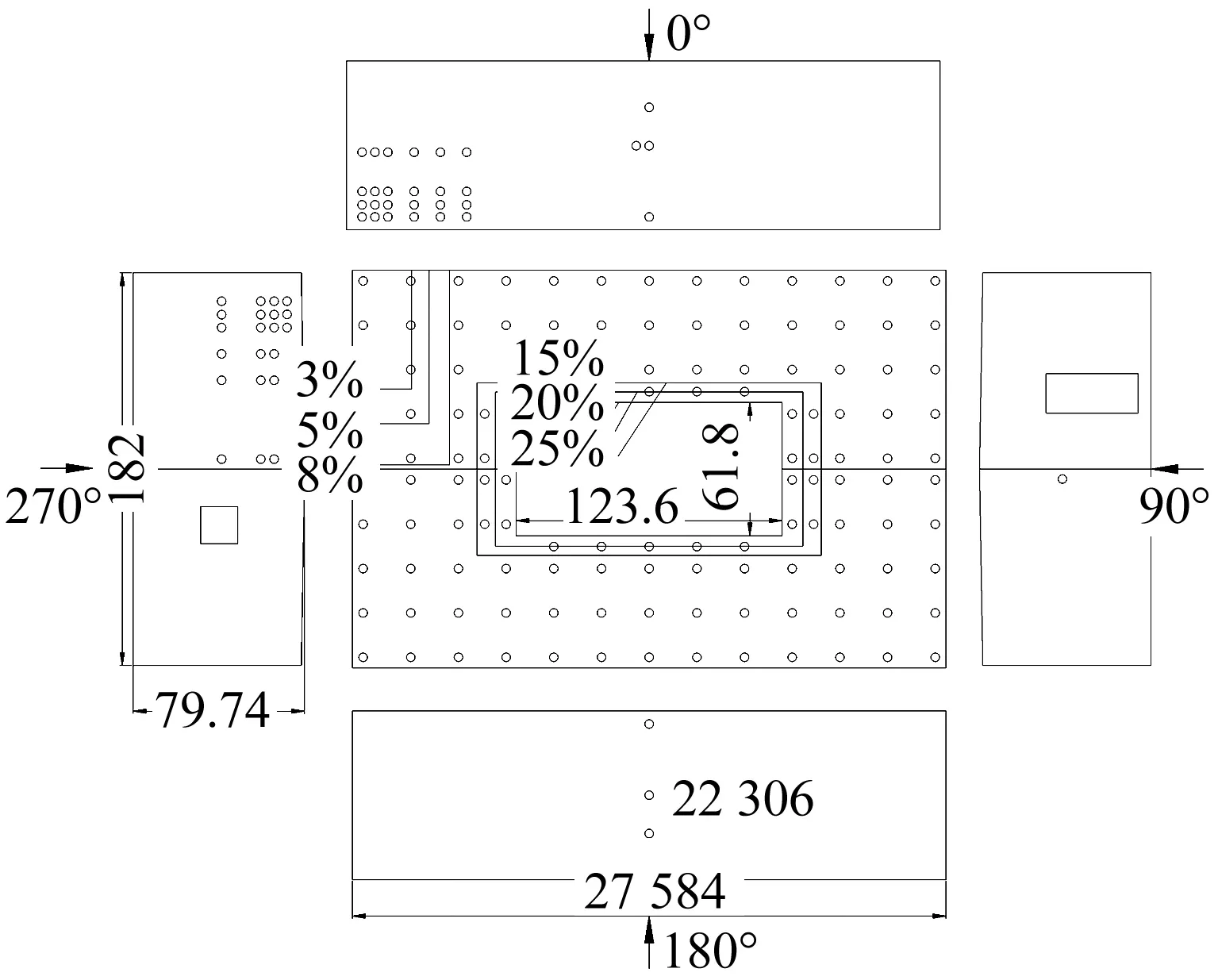
图2　试验模型测点布置图Fig.2　Tap location of test model

2　风致内压的空间分布特性和相干性

图3给出了工况1和工况4时0°风向角下屋盖下表面平均风压系数分布。由图3可知，工况1屋盖下表面风压系数分布均匀且非常接近，在-0.30～-0.32之间分布，可采用统一的平均风压系数来描述内部平均风压，误差小于8%。相应于角部开孔工况，对于工况4，屋盖下表面风压也表现为较均匀的负风压分布，在-0.78～-0.82范围内变化，数值的变化范围在7%以内，内部平均风压亦可采用统一的平均风压系数来描述。但屋盖角部开孔时建筑内部平均风吸力明显大于屋盖中心开孔工况。

图3　工况1和工况4的屋盖平均风压系数(0°风向角)Fig.3　Mean wind pressure coefficients on case No.1 and case No.4

图4给出了工况1和工况4时0°风向角下屋盖下表面脉动风压系数分布。由图4可知，下表面风压脉动较小且较均匀，工况1的脉动风压系数为0.12～0.15，工况4的脉动风压系数为0.148～0.154,且分布均匀。工况1和工况4脉动风压系数的变化范围均在8%以内，内部脉动风压可采用统一脉动风压系数来描述。故在后文中以屋盖所有下表面测点平均风压系数或脉动风压系数的平均值，用以描述屋盖开孔建筑的内部平均或脉动风压系数。

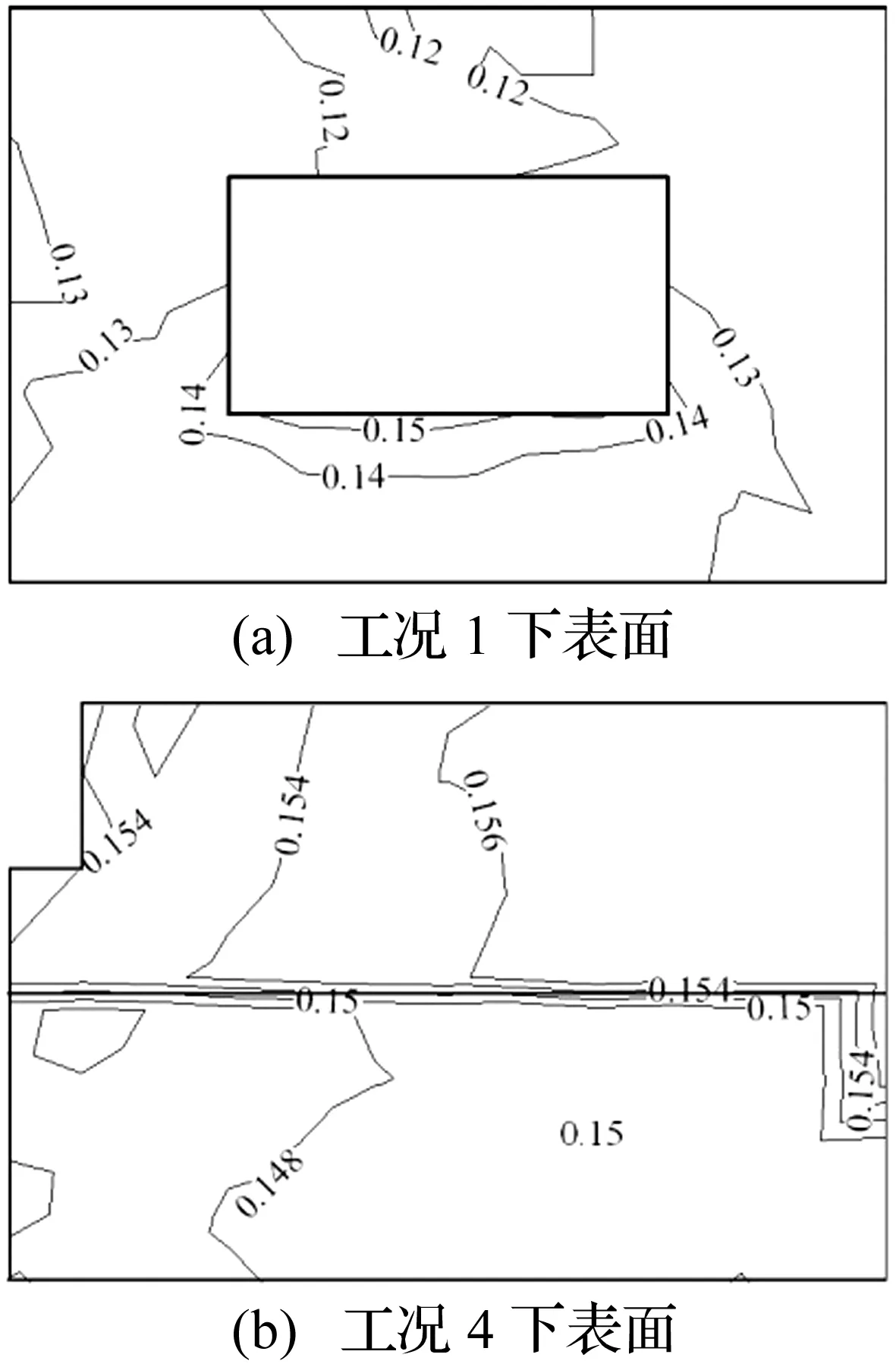
图4　工况1和工况4的屋盖脉动风压系数(0°风向角)Fig.4　Fluctuating wind pressure coefficients on case No.1 and case No.4

为了进一步明确内压取值方法，图5从频域上进一步研究了屋盖开孔建筑的内压相干函数。图5(a)给出了工况1下0°、45°和90°风向角时内风压系数相干函数曲线。从图5(a)可知，在0°风向角时，内风压系数相干函数幅值在0～3 Hz频率范围内大于0.9；在45°斜风向时，内风压系数相干函数曲线幅值在0～0.86 Hz内大于0.9，而在0.86～3 Hz这段区域内波动较大，但幅值大于0.8；在90°风向角时，内风压系数相干函数曲线幅值在0～1.9 Hz频率范围内大于0.9。比较0°和90°风向角的内风压系数相干函数可知，屋盖顶部开孔顺风向越宽，其相干性越差，而在45°斜风向时，受锥形涡的影响，导致其内部风压的相干性下降。但总体上来说，屋盖中心开孔的建筑内风压系数相干函数幅值在主要频率范围均接近1.0，相关性较好，进一步说明内部风压可以采用统一时程表示。

图5(b)给出了工况4下0°、315°和270°风向角时内风压系数相干函数曲线。从图5(b)可知，0°风向角时，内压相干函数幅值在0～3 Hz频率范围内大于0.98；270°风向角时，内风压系数相干函数幅值在0～3 Hz频率范围接近1.0，频率大于3 Hz时相干函数开始衰减；斜风向315°时，在0～3 Hz以内相干函数幅值接近于1.0。对比3个典型风向角的内风压相干函数可知，屋盖角部开孔建筑的内部风压高度相关，进一步说明内压可采用统一时程表示，且角部开孔的工况的内风压相干性要高于中心开孔的工况。

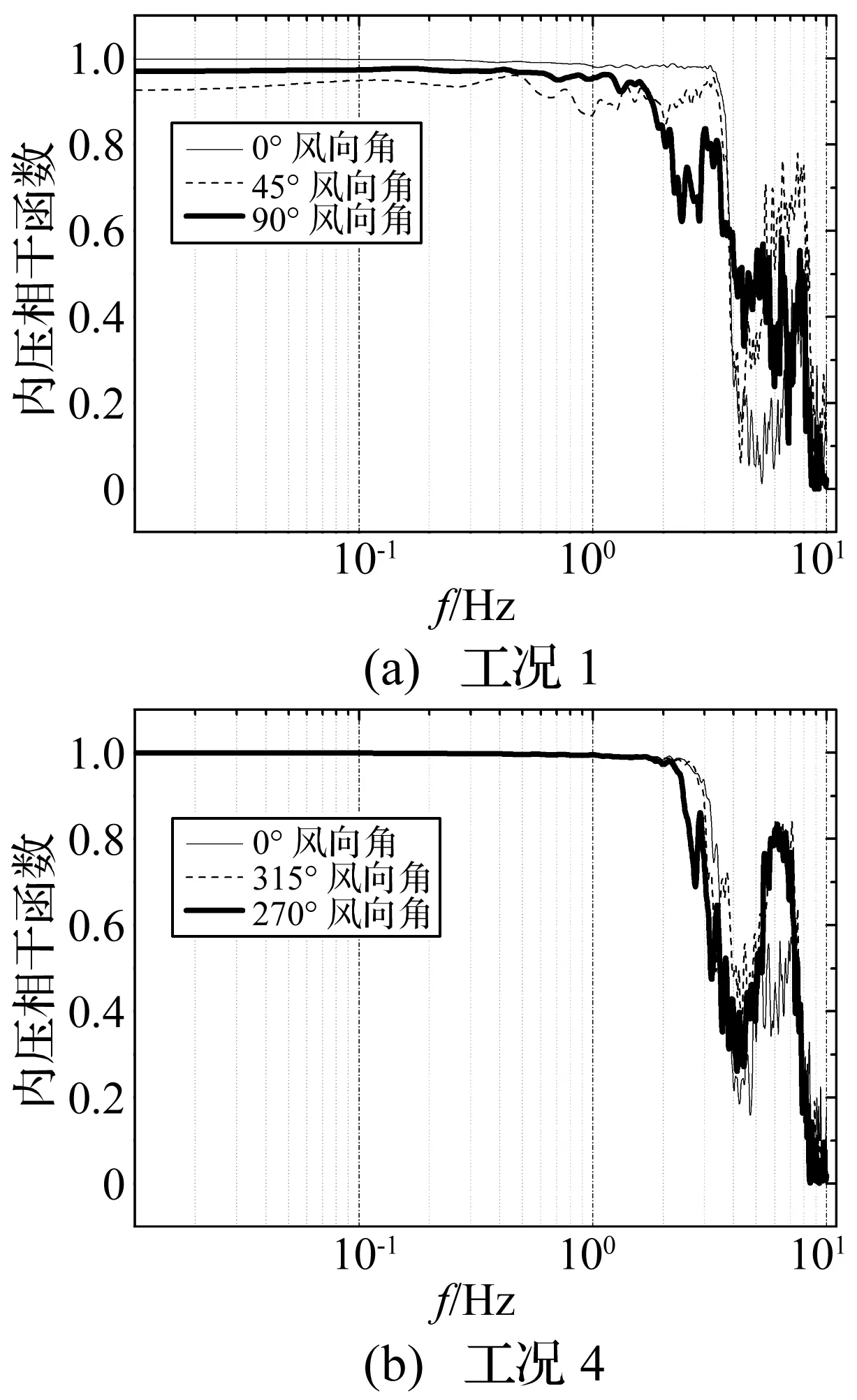
图5　内风压系数相干函数Fig.5　Coherence of internal wind pressure coefficients

3　内外风压的相关性分析

内外风压的相关系数是衡量风压联合作用的重要参数，在决定屋面覆面材料等围护结构设计时，起着重要的作用。图6给出了工况1屋盖在0°、45°和90°风向角时的上下表面风压之间的相关系数分布等值线图。由图6可知，对于垂直风向0°和90°时风向角时，屋盖上下表面风压相关系数分别为-0.15～0.55和-0.40～0.50，最大相关系数发生在屋盖开孔处，最小相关系数发生在尾流区后半屋盖，此时上下表面风压基本不相关；对于斜风向45°风向角时，屋盖上下表面风压相关系数为-0.30～0.80，最大相关系数(0.80)发生在屋盖开孔处锥形涡侧，屋盖上下表面风压联合作用明显。

图7给出了工况4屋盖在0°、270°、315°、45°、90°和180°风向角时的上下表面风压之间的相关系数分布等值线图。由图7可知，0°、270°、315°、45°、90°和180°风向角时屋盖上下表面风压相关系数分别为0～0.6、-0.05～0.75、0.1～0.75、0～0.55、0～0.45、0～0.55，最大相关系数均出现在屋盖开孔处，尾流区屋盖相关系数较低。最大相关性发生在315°风向角，达到0.75，屋盖上下表面风压联合作用明显。

SHARMA通过试验研究表明立墙开孔的屋盖内外风压系数之间的相关性最高为-0.6，且以负相关为主，BESTE和CERMARK通过风洞试验表明立墙开孔的建筑屋盖边缘区域和角部区域的相关系数最高为-0.5[12]。结合图6和图7与以往立墙开孔的试验结果对比发现，屋盖开孔的建筑内外风压系数相关性以正相关为主，中心开孔工况最大相关系数为0.80，角部开孔工况最大相关系数为0.75，相关程度要高于立墙开孔工况。

图6　工况1屋盖上下表面风压相关系数(开孔率15%)Fig.6　Correlation coefficients between upside and downside wind pressure on case No.1

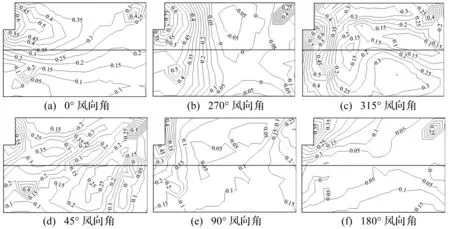
图7　工况4屋盖上下表面风压相关系数(开孔率3%)Fig.7　Correlation coefficients between upside and downside wind pressure on case No.4

4　风致内压的理论估计

4.1内压估计方法

稳态方法被广泛用于估计背景泄漏、多开孔建筑的内部平均风压。假设建筑开孔处为理想的定常不可压缩流体，由伯努利理论可得多个开孔时的建筑内部平均风压系数：

(1)

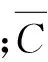
(2)

单开孔建筑脉动内压估计通常是通过求解单开孔内压传递方程实现。单开孔内压传递方程为：

(3)

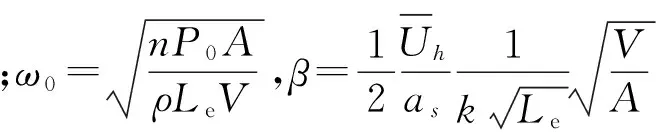
式(3)为二阶非线性微分方程，为了求解方便，许多学者提出了阻尼项线性化方法，其中最常用的为能量平均和概率平均线性化方法，线性化阻尼后便可采用频域法进行求解。然而，对于非线性方程，时域求解方法被广泛采用。本文采用四阶龙格-库塔法从时域求解式(3) 。

4.2内压的估计结果

表2给出屋盖中心开孔的工况1、工况2、工况3、工况8、工况12、工况13、工况17时0°风向角的平均和脉动内压的理论估计结果。由表2可知，在风向角为0°时，采用稳态方法可以较好地估计平均内压，估计误差较小，最大估计误差为12.77%，发生在工况2，其余工况的估计误差均小于10%；采用单开孔内压传递方程可以较好的估计脉动内压，多数工况下估计误差均小于15%，仅在工况3，脉动内压估计误差最大，为23.08%。

表3给出屋盖中心开孔的工况1、工况2、工况3、工况8、工况12、工况13、工况17时45°风向角的平均内压和脉动内压估计结果。由表3可知，在风向角为45°时，内压与外压的测点相关性较低，采用稳态方法估计斜风向平均内压误差较大，发生在工况2；采用单开孔内压传递方程可以较好的估计脉动内压，多数工况下估计误差均小于15%，只在工况13脉动内压估计误差最大，为25%。对比0°和45°风向角的内压估计结果可知，垂直风向0°风向角的内压估计性能优于45°斜风向。

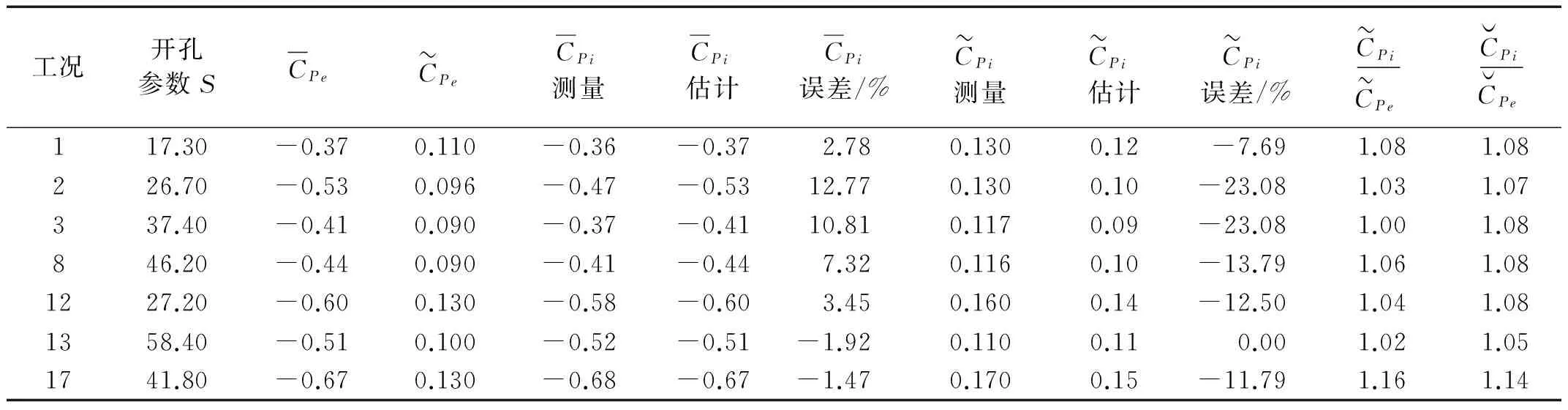
表2　内压试验值与理论估计值(0°风向角)

表4～表6给出屋盖角部开孔的工况4、工况5、工况6、工况9、工况10、工况11、工况14、工况15、工况16在0°、315°和90°风向角的平均和脉动内压的理论估计结果。由表4～表6可知，当开孔迎风(0°、315°)时，由于驱动内压的外部风压测点定义只有孔口的背风向测点，所以此时内压的理论估计性能一般，其平均内压估计的最大误差为25.42%，发生在工况11， 且315°风向角的估计误差大于0°，脉动内压估计的最大误差为33.33%；当开孔背风(90°)时，此时气流由外部平均测点流向结构内部，内压的理论估计性能优于开孔迎风风向角，其平均内压估计的最大误差为20%，发生在工况5，脉动内压估计在90°风向角的多数工况的估计误差均在16%以内，最大估计误差发生在工况5，最大误差为40%。

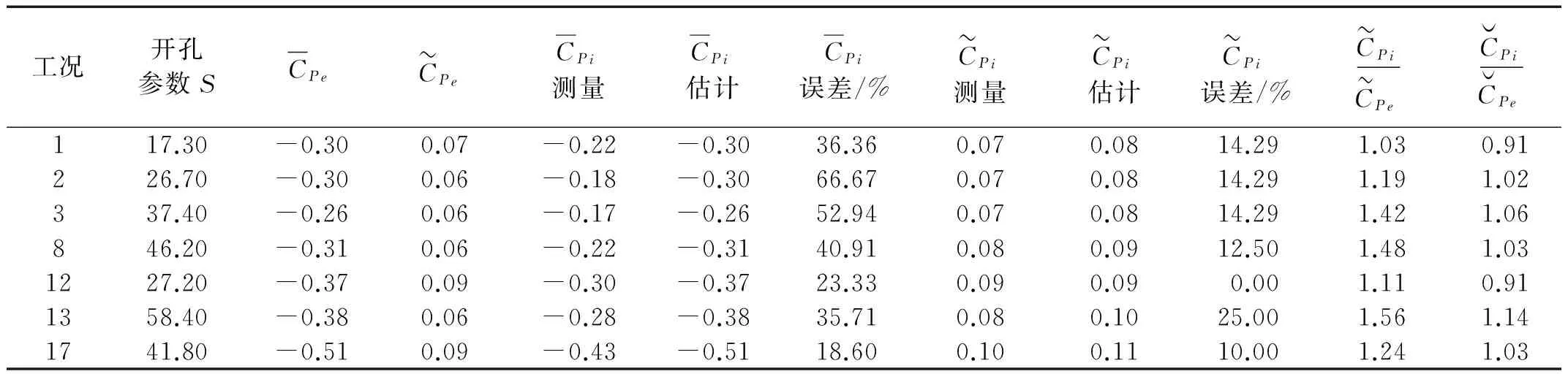
表3　内压试验值与理论估计值(45°风向角)

表4　内压试验值与理论估计值(0°风向角)

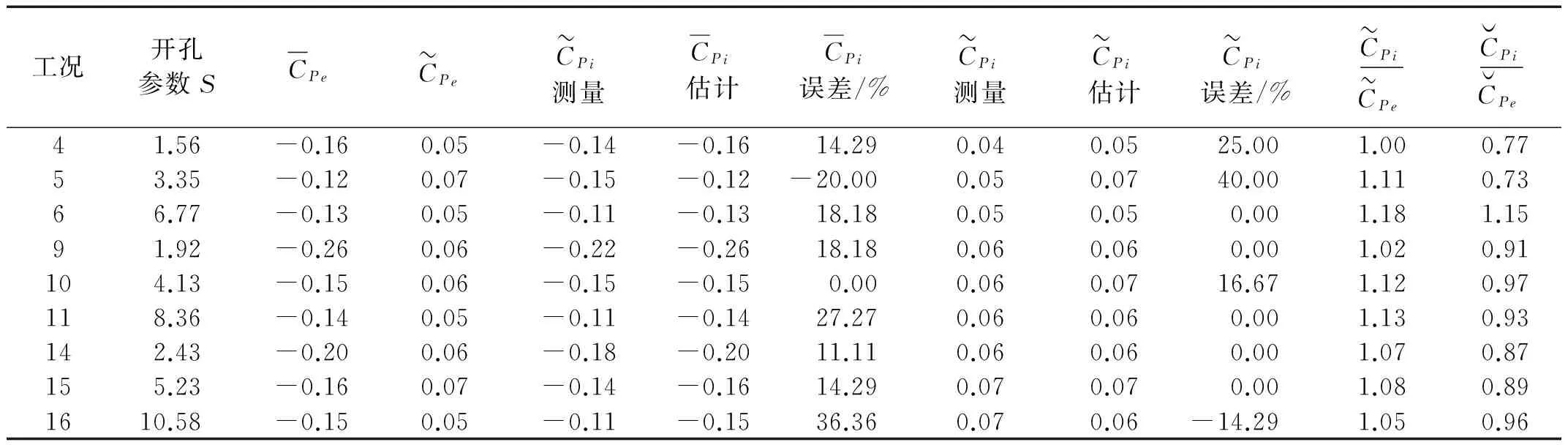
表6　内压试验值与理论估计值(90°风向角)

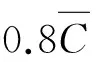
5　风致内压的无量纲设计公式

5.1脉动内外压系数比的拟合

VICKERY和BLOXHAM对阻尼进行了线性化，并采用稳态流假定取耗散系数k=0.61，通过频域方法对式(3)进行求解。求解过程中，假定高频的HELMHOLTZ共振可以从低频的背景响应中进行分离，假定外压功率谱为KARMAN谱、外脉动风压系数为0.35，得到了立墙开孔建筑的脉动内外压系数比为：

(4)

IRWIN和DUNN忽略内压传递方程的惯性项，推导了立墙开孔建筑的脉动内外压系数比[15]：

(5)

式中:τ为瞬态内压响应时间;其相应数值由式(6)决定：

(6)

HOLMES则对一系列的试验数据进行了拟合，得到了立墙开孔的脉动内外压系数比的经验公式为[13]：

(7)

在本文试验中开孔参数S的取值为17.3～58.4，式(7)对本文试验并不适用。本文对屋盖中心开孔0°风向角试验数据进行最小二乘公式拟合，得到屋盖中心开孔建筑脉动内外压系数比的经验公式为：

(8)

基于本文屋盖中心开孔参数S，假定湍流积分尺度为75 m，耗散系数k为0.15，利用VICKERY和BLOXHAM(1992)方法，IRWIN和DUNN(1993)方法和本文的拟合公式求得脉动内外压系数之比绘制于图8。由图8可知，VICKERY方法高估了屋盖开孔建筑的脉动内外压系数比，IWIN方法由于忽略流体惯性而低估了屋盖开孔建筑的脉动内外压系数比，本文的拟合公式对屋盖开孔建筑的脉动内外压系数比做出了较好的估计，且相应于以往方法具有更高的保证率。

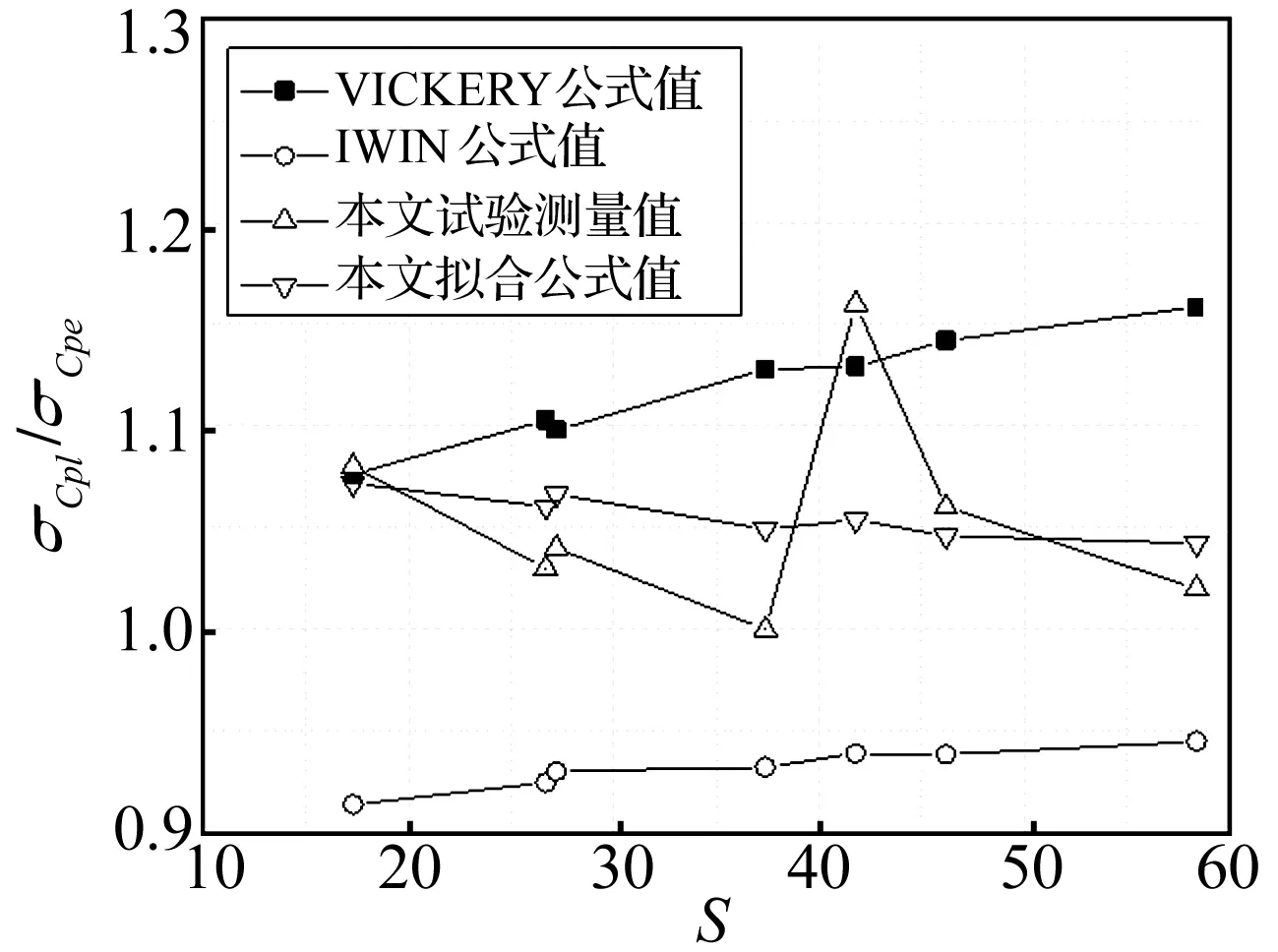
图8　屋盖中心开孔建筑的脉动内外压系数比Fig.8　The ratio between fluctuating internal pressure and external pressure

5.2峰值内外压系数比的拟合

为了设计需要，ASCE(2005)规范给出了开孔结构峰值内外压系数比的公式：

(9)

式中：Vi为建筑内部体积；Aog为开孔面积。由于其忽略惯性项，故式(9)得出的结果<1，采用该式将低估屋盖开孔建筑峰值内外压系数比。

GINGER在基于来流通过迎风面开孔的风洞试验基础上给出了类似开孔结构的峰值内外压系数比为[14]：

(10)

式中：g为峰值因子，可由相应峰值因子方法获得，通常取值为3.5～4；Iu为来流湍流度。

本文基于试验数据，对试验数据进行最小二乘拟合，得到屋盖开孔建筑的峰值内外压系数比的拟合公式为：

(11)

图9给出了GINGER和本文试验以及本文拟合公式计算得到的峰值(极小值)内外压系数比。由图9可知，GINGER方法低估了屋盖中心开孔建筑的峰值内外压系数比，本文拟合的公式可以对屋盖中心开孔建筑的峰值内外压系数比做出较好的估计，与试验获得值比较接近，改进了GINGER方法的精度。

图9　屋盖中心开孔建筑的峰值内外压系数比Fig.9　The ratio between peak internal pressure and external pressure

6　结　论

(1) 屋盖开孔建筑的屋盖下表面受均匀的风吸力作用，相干性好，内部风压系数可采用统一的值来描述。

(2) 屋盖开孔建筑的内外风压系数以正相关为主，屋盖中心开孔工况最大相关系数为0.80，屋盖角部开孔工况最大相关系数为0.75，相关程度高于立墙开孔工况。

(3) 采用稳态方法估计屋盖开孔建筑的内部平均风压的估计误差≈20%，建议屋盖单开孔建筑的平均内压设计值可取为0.8倍开孔处外部平均风压，我国规范低估了屋盖开孔建筑内部平均风压。

(4) 采用单开孔内压传递方程估计屋盖开孔建筑的内部脉动风压，垂直风向0°风向角的中心开孔工况和90°风向角的角部开孔工况估计误差小于15%。

(5) 基于无量纲开孔参数和湍流度参数，本文拟合了脉动内外压系数比和峰值内外压系数比的设计公式，改进了GINGER方法的精度，可运用于工程设计。

[1] HOLMES J D. Mean and fluctuating internal pressures induced by wind[C]// Proceeding 5th International Conference on Wind Engineering.Fort Collins, Colorado: Pergamon Press,1979: 435-450.

[2] LIU H, SAATHOFF P J. Building internal pressure: sudden change[J]. Journal of the Engineering Mechanics Division,1981,107(2):309-321.

[3] VICKERY B J, BLOXHAM C. Internal pressure dynamics with a dominant opening[J]. Journal of Wind Engineering and Industrial Aerodynamics,1992, 41(1/2/3):193-204.

[4] SHARMA R N, RICHARDS P J. Computational modelling of the transient response of building internal pressure to a sudden opening[J]. Journal of Wind Engineering and Industrial Aerodynamics,1997,72:149-161.

[5] 余世策.开孔结构风致内压及其与柔性屋盖的耦合作用[D].杭州:浙江大学,2006.

[6] HOLMES J D, GINGER J D. Codification of internal pressures for builfing design[C]//Proc of the Seventh Asia-Pacific Conference on Wind Engineering. Taipei,2009: 8-12.

[7] SHARMA R N, RICHARDS P J. Net pressures on the roof of a low-rise building with wall openings[J]. Journal of Wind Engineering and Industrial Aerodynamics,2005,93(4):267-291.

[8] 樊友川.典型工业厂房风荷载及其风振研究[D].上海:同济大学,2011.

[9] 余先锋, 全涌, 顾明. 开孔两空间结构的风致内压响应研究[J]. 空气动力学学报, 2013, 31(2):151-155.

YU Xianfeng，QUAN Yong，GU Ming. Study on responses of wind-induced internal pressure in a two-compartment building with a dominant opening[J]. Acta Aerodynamica Sinica,2013, 31(2):151-155.

[10] 徐海巍, 余世策, 楼文娟. 迎风墙面多开孔结构风致内压的试验研究[J]. 振动与冲击, 2014, 33(15):82-87.

XU Haiwei，YU Shice，LOU Wenjuan. Tests for wind-induced internal pressure of a building with multiple openings on its windward wall[J]. Journal of Vibration and Shock, 2014,33(15):82-87.

[11] 李寿科.屋盖开孔的近地空间建筑的风效应及等效静力风荷载研究 [D].长沙:湖南大学.

[12] BESTE F, CERMAK J E. Correlation of internal and area-averaged external wind pressures on low-rise buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics,1997,69:557-566.

[13] HOLMES J D, GINGER J D. Internal pressures—the dominant windward opening case—a review[J]. Journal of Wind Engineering and Industrial Aerodynamics,2012,100(1):70-76.

[14] GINGER J D, HOLMES J D, KIM P Y. Variation of internal pressure with varying sizes of dominant openings and volumes[J]. Journal of Structural Engineering,2010,136:1319-1326.

[15] IRWIN P A , DUNN G. Review of internal pressures on low-rise buildings[R]. RWDI Report 93-270. In:Report to Canadian Sheet Steel Institute, Rowan, Williams, Davies and Irwin Inc., Guelph,Ontario,1993:451-480.

Wind tunnel tests on internal pressures of buildings with a roof opening

LI Shouke1, TIAN Yuji2, LI Shouying3, CHEN Zhengqing3, SUN Hongxin1

(1. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;2. Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, Beijing Jiaotong University, Beijing 100044, China;3. Hunan Provincial Key Laboratory of Wind Engineering and Bridge Engineering，Hunan University，Changsha 410082，China)

The effects of seventeen roof opening configurations on the internal pressures in a typical TTU building were examined by wind tunnel tests with the volume-scaled method. The configurations examined are of different opening locations and sizes, as well as the different volumes of internal spaces. The spatial distributions of the internal and external pressures and the correlations between them were specially studied. Theoretical methods for estimating the mean and root-mean-square of internal pressures were introduced, and a dimensionless formula for peak internal pressure coefficients ratio was fitted. The results show that the internal pressures in roof opening buildings are highly correlative and coherent, so the internal pressure coefficients in roof opening building can be described by using a unified value. The correlation coefficients between external and internal pressure coefficients are positive, and larger than those in wall opening cases. The mean external pressure coefficients around the opening multiplied by 0.8 can be used to estimate the mean internal pressure coefficients. For single dominant opening buildings, the Helmholtz equation can be used to simulate the fluctuating internal pressure, and the estimation error is below 15% for the wind in vertical orientation. The empirical formulas about the ratio between fluctuating internal pressure and external pressure, and the ratio between peak internal pressure and external pressure were fitted with the non-dimension opening parameters, which are more effective than other methods，such as GINGER method and HOLMES method.

wind tunnel test; roof opening; correlation coefficients; peak internal pressure

国家自然科学基金资助(51508184)；湖南省高校创新平台开放基金资助(湘教通(2012)595)；北京交通大学结构风工程与城市风环境北京市重点实验室开放基金资助；长沙理工大学桥梁工程安全控制技术与装备湖南省工程技术研究中心开放基金资助;湖南省自然科学基金资助(2016JJ3063 )

2015-07-02修改稿收到日期：2015-09-15

李寿科 男，博士，副教授,1981年生

TU119+.21

A DOI:10.13465/j.cnki.jvs.2016.14.001