具有结构非线性的折叠机翼气动弹性分析

倪迎鸽， 侯　赤， 万小朋， 赵美英

(西北工业大学 航空学院，西安　710072)



具有结构非线性的折叠机翼气动弹性分析

倪迎鸽， 侯赤， 万小朋， 赵美英

(西北工业大学 航空学院，西安710072)

分析了具有铰链间隙的折叠机翼的非线性气动弹性响应。首先采用模态综合法建立了折叠机翼的结构动力学模型，其次基于偶极子非定常空气动力模型，由最小状态法有理函数近似获得了时域下气动力近似表达式，最后通过Runge-Kutta法获得了时域的气动弹性响应。分析表明：由于铰链处间隙的存在改变了折叠机翼气动弹性性能，使得结构在一定的速度范围内产生极限环运动，但是内外铰链对间隙大小的敏感程度有所不同;通过加入铰链间的摩擦来改善铰链间隙对气动弹性性能的影响，计算表明摩擦能够有效地降低振动幅值，是有益的非线性。

折叠机翼；结构非线性；非定常气动力；有理函数近似；气动弹性响应

折叠机翼的机身与翼面以及翼面之间通常为铰链连接，不可避免地存在间隙与摩擦，改变了机翼的气动弹性性能。LEE等[1]运用ZAERO和MSC.NASTRAN软件，采用数值积分的方法分析了具有双线性间隙非线性的折叠机翼的气动弹性响应，获得了折叠机翼产生极限环振荡的条件。BAE等[2-3]和LEE等[4-5]结合虚质量法和描述函数法对具有操纵面的机翼结构的间隙非线性气动弹性响应进行了分析，结果表明非线性的存在改变了机翼结构的颤振特性，在不同的速度区间会产生极限环振荡。杨智春[6]分析了二翼段的结构非线性颤振现象，并进行实验研究，结果表明：描述函数、数值积分等方法的计算结果与实验相吻合。同样，针对摩擦非线性也有不少研究[7-9]，MIGNOLET等研究表明摩擦可以作为稳定因子，在一定条件下，可以减弱极限环运动。

但是对于间隙非线性的的气动弹性分析均采用简单的工程结构进行理论分析，摩擦非线性同样也是基于二元翼模型[10]。因此对于多自由度具有间隙非线性的折叠机翼的气动弹性分析，其重点在于如何建立多自由度非线性气动弹性模型，以及利用非线性模型预测折叠机翼的气动弹性现象。与线性模型相比，非线性模型的气动弹性现象比较复杂，这给折叠机翼的强度设计也带来了严重的问题。因此，即使利用非线性模型预测到折叠机翼的气动弹性响应，如何解决折叠机翼的强度设计也是有待解决的问题。

本文基于固定界面模态综合法，将折叠机翼的内部自由度转换到模态空间中，界面处非线性自由度仍保留在物理空间中，结合有理函数近似得到的时域气动力模型，建立了折叠机翼结构的间隙非线性气动弹性表达式。在获得间隙非线性气动弹性现象基础上，通过在铰链处增加摩擦力矩来抑制间隙非线性对折叠机翼的气动弹性响应的影响。

1　折叠机翼非线性气动弹性模型的建立

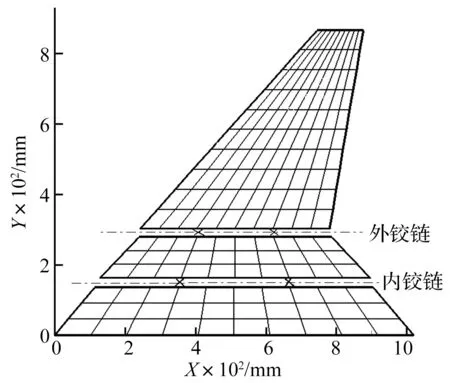
图1　折叠机翼有限元模型(图中X代表铰链所处的位置)Fig.1　Finite element model of a folding wing(x represents the position of hinges)

1.1结构模型的建立

对于具有铰链间隙的折叠机翼，随着间隙位移的变化，结构的动力学特性也发生变化。虽然间隙非线性自由度占结构总自由度的小部分，但其却影响整个结构的动力学特性，同时相应的非定常气动力也需要重新计算。因此在建立折叠机翼非线性模型时，本文采用模态综合法建立结构模型，将非线性自由度即界面处通过扭转弹簧耦合的θx自由度仍保留在物理空间。

折叠机翼的子结构无阻尼的动力学方程如下所示：

(λ=A,B,C)

(1)

式中：Mλ，Kλ分别为各个子结构质量矩阵与刚度矩阵，uλ为各个子结构的位移。fλ为子结构界面处的约束力。

为了方便模态综合法[11-12]的应用，将各个子结构的节点位移分为内部节点位移和界面节点位移，对质量矩阵和刚度矩阵进行相应的分块。在本文的模型中，界面处的铰链是通过MPC和扭转弹簧来模拟，所以将将界面节点位移分成了两部分，即MPC耦合的节点位移和扭转弹簧耦合的节点位移。以子结构A为例，其动力学方程为：

(2)

式中：i代表内部节点位移;m代表MPC耦合的节点位移;s代表扭转弹簧耦合的节点位移。

对于子结构A进行模态分析，引入模态坐标pA以及模态矩阵φA，则：

(3)

类似地，引入模态坐标pB,pC以及模态矩阵φB,φC，对于子结构B和子结构C进行相应的模态分析。此时，整体的折叠机翼结构动力学方程可以写成如下形式：

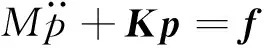
(4)

式中：

M=diag(φATMAφA,φBTMBφB,φCTMCφC)

K=diag(φATKAφA,φBTKBφB,φCTKCφC)

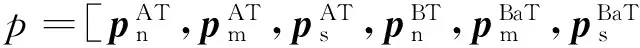
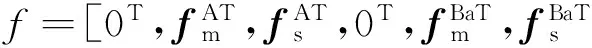
a代表子结构A与B的边界，即内铰链，b代表子结构B与C的边界, 即外铰链。

此时，p中各个分量并不独立，对各个子结构进行综合，消去非独立的模态坐标便可以得到整体结构的动力学方程。值得注意的是，界面处的位移协调条件与固接的协调条件有所不同，其位移协调条件如下所示：

(5)

式中：θa，θb为各个子结构界面处扭转角θx差值，即内铰链和外铰链处的广义位移。在本文的模型中共有4组铰链，(见图1)。引入独立模态坐标变换矩阵Π，并左乘ΠT，则独立模态坐标下整体的动力学方程为：

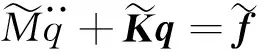
(6)

式中：

此时，对于界面处MPC耦合的自由度，其约束力是作用力与反作用力，综合之后为零；而对于界面处扭转弹簧耦合的自由度，其非线性约束力fa，fb是铰链处广义位移的非线性函数。

1.2气动力模型

偶极子网格法作为亚音速非定常气动力的计算方法，不仅适用于复杂几何形状的升力面，而且可以考虑多翼面的相互干扰、翼身组合体等问题，因此得到了广泛的应用。同时，对于存在间隙的这种局部非线性问题，该模型也可以准确地描述其气动力。本文采用偶极子网格法获得了折叠机翼的气动力模型。此时作用在结构网格节点的等效力：

(7)

式中：ρ为空气密度;V为速度;Q为气动力影响系数矩阵，通常是马赫数Ma和减缩频率k的函数。

将结构的位移u转换到模态坐标p时，则广义的气动力可以表达成：

(8)

1.3气动弹性方程的状态空间形式

对气动力进行独立模态坐标变换，得到整体的气动弹性方程的状态空间形式为：

(9)

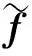
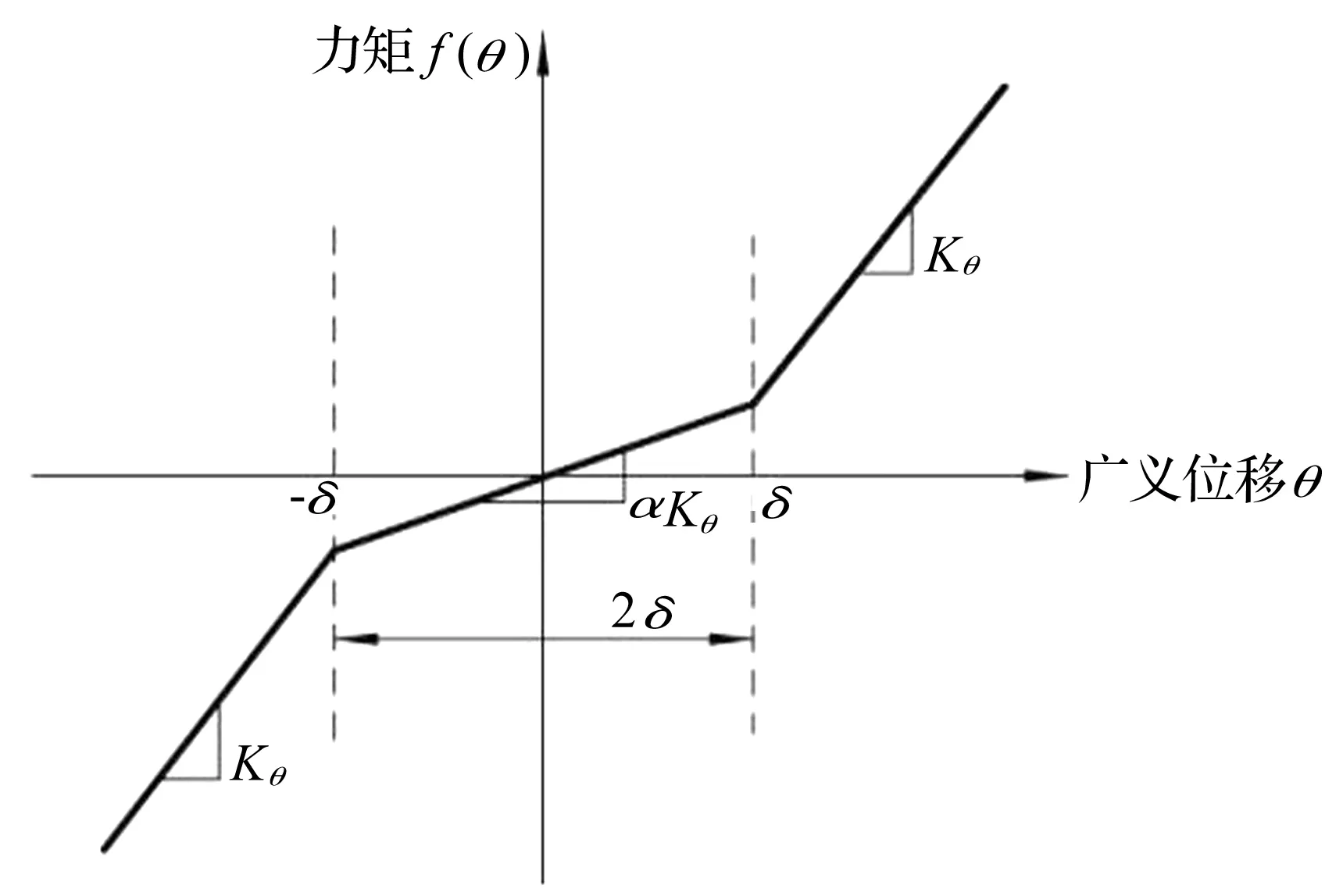
图2　间隙非线性[2]Fig.2　Freeplay nonlinearity

其表达式为：

(10)

式中：δ为间隙量；α为刚度系数。当间隙量δ=0时，则力矩变为θ的线性函数。

为了建立状态空间的气动弹性模型，需要进行有理函数近似来获得时域的气动力，如Roger 法，最小状态法等。在最小状态法中，引入的气动力状态变量数目少，得到的状态空间方程的阶次较低，并且精度较高[13]。因此这里采用最小状态法进行频域气动力的有理近似，引入气动力状态变量qa，气动弹性方程的状态空间的形式为：

2　讨论与分析

折叠机翼的各个子结构的质量矩阵和刚度矩阵通过DMAP语言获得。采用偶极子网格法获得折叠机翼在频域下的气动力，通过最小状态近似，获得了气动弹性方程在状态空间的表达形式。采用固定界面模态综合法时，对每个子结构均保留了6阶内部振动模态，界面处通过MPC(Multi-Point Constraint)和扭转弹簧相互耦合10个自由度，保留2个非线性自由度，得到的整体的动力学方程为46阶，引入4个气动力状态变量之后，最终得到状态空间的气动弹性方程，即式(11)为96阶，最后在MATLAB中采用Runge-Kutta法得到了折叠机翼时域的气动弹性响应。

2.1模型验证

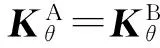
表1　固有频率的对比结果

对比完频率后之后，对模态振型进行了相关计算。各阶模态对应的振型对比(见图3)。本文方法获得的模态与MSC.NASTRAN获得的结果基本保持一致，从而在后面的应用过程中可以得到相关节点的准确位移。

图3　典型模态比较(左:本文方法计算结果,右: MSC.NASTRAN计算结果)Fig.3　Comparison of typical mode shapes (left: using this method; right: using MSC.NASTRAN)

在进行颤振边界的计算时，ρ=1.226 kg/m3,Ma=0.0。将直接时域的仿真结果与MSC.NASTRAN的结果进行对比(见表2)。颤振边界的对比结果表明：本文方法是满足工程精度要求的。

表2　颤振边界的对比结果

2.2间隙非线性气动弹性分析

为了明确间隙非线性对于折叠机翼气动弹性的影响。针对内外铰链，计算了3个间隙量，分别为δ=0.02°，δ=0.2°，δ=1.0°， 对于每个间隙量又分别采用了三种刚度系数，即α=0.0，α=0.1，α=0.2，共9种非线性条件进行分析。铰链处的初始广义位移均为0.1°，获得了折叠机翼间隙非线性气动弹性响应。

2.2.1内铰链有间隙非线性，外铰链无间隙非线性

对于线性气动弹性响应，当速度小于线性颤振速度时，线性气动弹性系统表现为衰减运动；当速度大于线性颤振速度时，线性气动弹性系统表现为发散运动。而间隙造成的非线性气动弹性响应表现为极限环运动，甚至出现混沌运动，并且大多在小于线性颤振速度的情况下出现。通过计算可知，当内铰链具有间隙非线性时，可以出现4种运动形式，其运动形式分布(见图4)，此时Vf=31.95 m/s(即本文方法获得的线性颤振速度)。

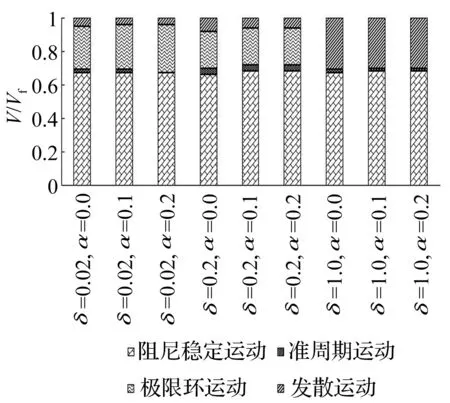
图4　运动形式分布图(内铰链具有间隙非线性)Fig.4　Motion map of folding wing with freeplay at the inboard hinge

从图4可知，对于δ=0.02°和δ=0.2°均可以出现4种运动形式，即阻尼稳定运动，准周期运动(此时运动形式对初始条件敏感，如果初始值较小，运动则会收敛)，极限环运动(此时运动形式对初始条件不敏感)和发散运动；而对于δ=1.0°只出现了3种运动形式，没有出现极限环运动，从准周期运动直接过渡到发散运动，且发散运动所对应的速度范围明显增大。当速度较小时，由于空气动力的阻力作用(本文中的气动弹性模型没有考虑结构阻尼)，折叠机翼做阻尼稳定运动，最后趋于平衡点；当速度较大时，系统的运动趋于复杂，出现了准周期运动，极限环运动以及发散运动。

2.2.2内铰链无间隙非线性，外铰链有间隙非线性

与内铰链间隙非线性对气动弹性影响类似，外铰链具有间隙非线性时也出现了4种运动形式，其运动形式分布(见图5)，此时Vf=31.95 m/s(即本文方法获得的线性颤振速度)。

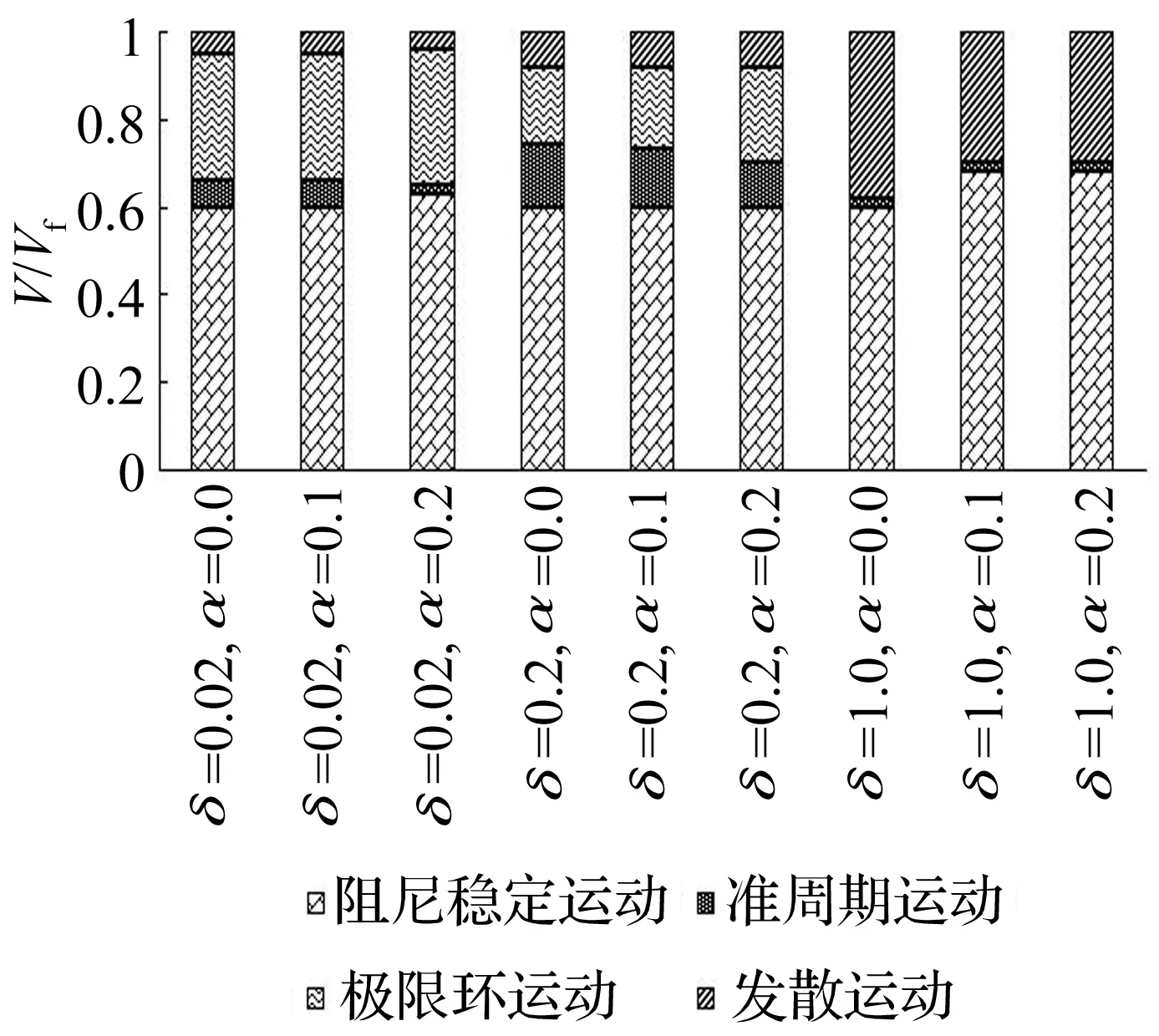
图5　运动形式分布图(外铰链具有间隙非线性)Fig.5　Motion map of folding wing with freeplay at the outboard hinge

通过图4和图5可知,即使在间隙量很小的情况下，极限环运动也会发生；当外铰链存在非线性时，阻尼稳定运动所对应的速度范围明显减小，同时准周期运动所对应的速度范围有所增大；当δ=1.0°时，在两种非线性状况下，均没有出现极限环运动；随着间隙量的增加，结构进入发散运动的速度减小；当间隙量相同时，随着α的增加，不同运动形式所对应的速度范围有所减小。

2.3间隙与摩擦非线性气动弹性分析

对于折叠机翼，铰链连接处不可避免地存在摩擦。在文献[7]也已证明摩擦可以作为一个稳定因子。因此为了减弱折叠机翼在间隙条件下产生各种非线性运动，本文能过摩擦力矩来减弱间隙非线性的影响。本文所采用文献[10]中的摩擦非线性，其模型见图6。

图6　摩擦非线性[10]Fig.6　Friction nonlinearity

其表达式为：

(12)

该非线性特点为：当δ′较小时，摩擦力矩f′(θ)等于摩擦刚度Kθ′与偏转角θ的乘积；当力矩大于f0时，摩擦刚度Kθ′为0，此时摩擦力矩保持定值。由于非线性气动弹性运动方程中的4个独立的非线性自由度均表达在物理空间中，所以只需要将摩擦非线性与间隙非线性进行物理叠加，便可以实现间隙与摩擦非线性气动弹性响应分析。

以δ=0.02°，α=0.0为例，铰链处的初始广义位移均为0.1°，图7给出了V=0.95Vf，f0=0.005 N·m，Kθ′=1 N·m/rad时的响应结果。从图7可知，摩擦非线性能够有效地减弱翼尖法向位移，使其从趋于发散的不稳定运动变为有限幅值的极限环运动。可以发现翼尖法向位移响应是以零位置为中心，这是由于间隙非线性和摩擦非线性均是中心对称的，物理叠加之后仍是中心对称。

图7　加入摩擦非线性气动弹性响应对比Fig.7　Comparison of aeroelastic responses between with and without friction

为了进一步明确摩擦非线性的物理参数对间隙非线性气动弹性的影响，本文分析了初始力矩f0，摩擦刚度Kθ′对间隙非线性气动弹性系统的影响(见图8)。

图8　摩擦非线性对间隙气动弹性的影响Fig.8　Effects of friction on aeroelastic responses of freeplay

从图8可知,随着初始力矩f0的增大，翼尖法向位移幅值在减小；随着摩擦刚度Kθ′的增大，翼尖法向位移幅值变化不大。对于图7(a)，此时Kθ′=1 N·m/rad，随着初始力矩f0的增大，δ′在增加，当增加到一定的程度时，初始力矩与间隙非线性引起的外力矩的作用是相反的，减弱了间隙非线性。对于图7(b)，此时f0=0.005 N·m，随着摩擦刚度Kθ′的增大，δ′在减小。在较小的位移范围内，Kθ′θ是起主要作用。所以在较大的位移范围内是初始力矩f0仍起主要作用。该现象说明：与摩擦刚度Kθ′相比，摩擦力矩对于响应幅值的降低有重要的作用。与此同时，当在外铰链处的间隙非线性中加入摩擦非线性时，翼尖法向幅值始终比在内铰链处的间隙非线性中加入摩擦非线性时的幅值要大。总之，在一定程度上，摩擦非线性能够有效地降低振动幅值，是有益的非线性。

3　结　论

本文提出了建立多自由度非线性的折叠机翼的气动弹性方法，并对该方法进行了准确性验证，最后分析了具有间隙和摩擦非线性的折叠机翼的气动弹性特性。可以得出以下结论：

(1) 结合固定界面模态综合法与偶极子空气动力模型，推导了一种具有多自由度非线性的气动弹性方程。该方法适用于分析具有多自由度气动弹性系统；另外，气动力不需要重新计算，简化了非线性气动弹性分析过程；

(2) 对于折叠机翼存在的间隙非线性，即使在间隙量很小的情况下，极限环运动也不可避免；在某些间隙量下，不会出现明显的极限环运动；当外铰链具有间隙非线性时，其位移的幅值明显要大于内铰链具有间隙非线性时的幅值，结构振荡加剧，对折叠机翼结构不利；

(3) 通过计算证明了摩擦可以抑制间隙非线性气动弹性的影响。对于间隙非线性的气动弹性响应，加入摩擦可以有效地减弱折叠机翼的间隙非线性强度；摩擦力矩对于响应幅值的降低有重要的作用，是一种有益的非线性。

[1] LEE D H, CHEN P C. Nonlinear aeroelastic studies on a folding wing configuration with free-play hinge nonlinearity[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Strcutural Dynamics & Materials Conference. Newport, RI, 2006。

[2] BAE J S, INMAN D J, LEE I. Effects of structural nonlinearity on subsonic aeroelastic characteristcs of an aircraft wing with control surface[J].Journal of Fluids and structures,2004(19):747-763.

[3] BAE J S,YANG S M, LEE I.Linear and nonlinear aeroelastic analysis of fighter-type wing with control surface[J].Journal of Aircraft,2002(39):697-708.

[4] LEE I, KIM S H. Aeroelastic analysis of a flexible control surface with structural nonlinearity[J].Journal of Aircraft,1995,32(4):868-874.

[5] KIM S H, LEE I. Aeroelastic analysis of a flexible airfoil with a freeplay non-linearity[J].Journal of Sound and Vibration,1996,193(4):823-846.

[6] 杨智春.结构非线性颤振的理论及试验研究[D].西安:西北工业大学,1987.

[7] SINHA A, GRIFFIN J H.Effects of friction dampers on aerodynamically unstable rotor staes[J].AIAA Jounral,1985,23:262-270.

[8] MIGNOLET M P, AGELASTOS A M, LIU D D. Impact of frictional structrural nonlinearity in the presence of negative aerodynamic damping[C]//44th AIAA/ASME/ASCE/AHS Structures, Strcutural Dynamics & Materials Conference. Norfolk, VA,2003.

[9] CHOI G G, AGELASTOS A M, MIGNOLET M P, et al. Effects of internal friction on the dynamic behavior of aeroelastic systems[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures, Strcutural Dynamics & Materials Conference. Palm Spring, CA,2004.

[10] 刘百慧, 李敏, 谭添才. 具有结构非线性的二元翼面颤振研究[J].工程力学,2013,30(4):448-454.

LIU Baihui, LI Min,TAN Tiancai.Flutter study of a two-dimensional airfoil with structual nonlinearities[J].Engineering Mechanics, 2013,30(4):448-454.

[11] CRAIG R R, BAMPTON C C. Coupling of substructures for dynamic analysis[J].AIAA Journal,1968,6(7):1313-1319.

[12] 王永岩.动态子结构方法理论与应用[M].北京:科学出版社,1999.

[13] 赵永辉. 气动弹性力学与控制[M].北京:科学出版社,2007.

Aeroelastic analysis of a folding wing with structural nonlinearities

NI Yingge, HOU Chi, WAN Xiaopeng, ZHAO Meiying

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The nonlinear aeroelastic response of a folding wing with freeplay at hinges was investigated. The structural dynamic model of the folding wing was established based on the modal synthesis method. An approximate expression of the aerodynamic force in time domain was obtained by virtue of the minimum state rational function approximation based on a doublet lattice unsteady aerodynamic model. The aeroelastic dynamic equation was solved using the Runge-Kutta method to provide the aeroelastic response in time domain. The results show that the aeroelastic characteristics of the folding wing are changed by the freeplay at hinges, which induces the limit cycle oscillation within a certain velocity range. But the sensitivities of the inboard and outboard hinges to the freeplay are different. The addition of friction to the hinges can improve the effect of the freeplay on the aeroelastic performance. The simulations show that the friction can reduce the oscillation amplitude effectively and is a beneficial nonlinearity.

folding wing; structural nonlinearities; unsteady aerodynamic force; rational function approximation; aeroelastic response

2015-06-24修改稿收到日期：2015-08-18

倪迎鸽 女，博士生，1987年生

万小朋 男，教授，1962年生

E-mail:wanxp@nwpu.edu.cn

V271.4

A DOI:10.13465/j.cnki.jvs.2016.14.027