大型复杂钢管焊接结构损伤识别新方法

郭俊龙， 马立元， 李永军， 王天辉

(军械工程学院 导弹工程系，石家庄　050003)



大型复杂钢管焊接结构损伤识别新方法

郭俊龙， 马立元， 李永军， 王天辉

(军械工程学院 导弹工程系，石家庄050003)

提出一种将Kriging代理模型和动力指纹方法相结合的大型复杂结构损伤识别两步法。首先建立结构响应与结构损伤参数之间的Kriging代理模型，代替结构原有有限元模型，对结构损伤进行全局识别，确定损伤位置;然后针对损伤结构，通过动力指纹方法，以结构单元模态应变能曲率差为指标，对结构损伤进行局部识别，确定损伤状况;最后，将该两步识别法应用于某导弹发射台模型的损伤识别中。实验结果表明，该方法可应用于工程实际，为大型复杂结构损伤识别提供了一种新思路。

大型复杂结构；损伤识别；Kriging代理模型；模态应变能曲率差

近年来，随着社会生产劳动对大型复杂结构依赖性的提高，结构损伤所造成的突发性毁坏事件给人们带来的直接或间接损失不可估量。因此，对复杂机械结构的损伤识别研究刻不容缓。目前常用的损伤识别方法包括基于模态信息的损伤识别方法[1]、基于模型修正的损伤识别方法[2]、基于智能科学的损伤识别方法[3]等，这些方法在简单结构的损伤识别中表现出很好的效果。然而，在对大型复杂结构进行损伤识别时，由于测量、建模误差，传感器布置等诸多因素的影响，使得损伤识别结果往往难以达到令人满意的效果，并且每种方法都有其适用范围和局限性，给大型复杂结构的损伤识别带来较大难题[4]。

本文将基于动力指纹的损伤识别方法与Kriging代理模型相结合，提出了一种大型复杂结构损伤识别两步法：① 通过建立结构的Kriging代理模型，对大型复杂结构进行损伤定位研究，初步确定损伤位置；② 以结构单元模态应变能曲率差为指标，对结构损伤进行局部识别，确定结构损伤状况。数值仿真及试验结果表明，本文所提两步法在大型复杂结构的损伤识别中具有良好的实用效果。

1　基于Kriging代理模型的结构损伤定位研究

Kriging代理模型是一种基于数理统计的估计方差最小的无偏估计模型，它是一种可以跳过复杂的有限元计算过程而直接建立结构响应与结构损伤参数之间关系的简化模型。它不仅考虑了待估点位置与已知数据位置的相互关系，而且考虑了变量的空间相关性[5]，仅需少量样本便能准确描述系统响应与系统输入之间的关系，常被用于金属矿探测[6]以及结构的优化设计[7]和结构稳健性设计[8]，在损伤识别领域应用还比较少见。

1.1理论基础

1.1.1Kriging代理模型

Kriging代理模型主要包括回归部分和非参数部分，对于给定的样本集{(x1,y1)，(x2,y2)，…，(xn,yn)}，x∈Rn，y∈R，某一未知点x的响应可由下式进行估计：

(1)

式中：

μ=(FTR-1F)-1FTR-1Y

FT=[f(x1),…,f(xn)]

Y=[y1,y2,…,yn]T

成功建立结构的Kriging代理模型后，一般采用平方相关系数SC和平方误差准则EISE对其精度进行评价。

(2)

(3)

MATLAB中提供了Kriging代理模型的工具箱DACE，可通过编写相应程序获得结构响应的Kriging代理模型。

1.1.2基于Kriging代理模型的损伤识别步骤

成功建立结构的Kriging代理模型后，则结构损伤识别问题转化为多目标优化求解问题，即在一定的搜索区域内，搜索一组损伤参数值，使得实际测得的结构响应与Kriging代理模型预估的结构响应误差最小，从而识别出损伤。由此建立目标函数如下：

(4)

具体识别步骤如下：

(1) 应用有限元软件建立结构的有限元模型，并进行修正，得到修正后结构的精准有限元模型；

(2) 采用拉丁超立方方法抽取若干组损伤参数值作为样本，并通过有限元软件计算对应损伤状况下的结构响应；

(3) 利用样本与其对应的响应建立结构的Kriging代理模型，得到结构输出响应与损伤参数值之间的关系；

(4) 通过式(2)、式(3)验证Kriging代理模型的准确性(SC>0.99，EISE<0.01)。若Kriging代理模型满足以上准则，则此时的代理模型可准确描述结构响应与结构损伤参数值之间的关系，否则，需要通过加点准则对Kriging代理模型进行修正；

(5) 重复步骤(4)，直至Kriging代理模型满足评价准则；

(6) 针对待识别工况，通过优化算法搜索一组损伤参数值使得目标函数达到最小值，则可求得对应待识别工况下的损伤状态。

1.2发射台骨架模型损伤定位实验

某发射台骨架实物图见图1，材料为Q235钢，弹性模量E=2.07×1011N/m2，泊松比μ=0.27，密度ρ=7 800 kg/m3，结构为瑞利阻尼。

图1　发射台骨架模型及传感器布置方案Fig.1　The launch platform model and the arrangement of sensors

建立发射台骨架有限元模型(见图2)，有限元建模时选用beam189单元，模型包含67个梁单元。建立好结构初始有限元模型后，需要对其进行模型修正，获得结构的精准有限元模型。

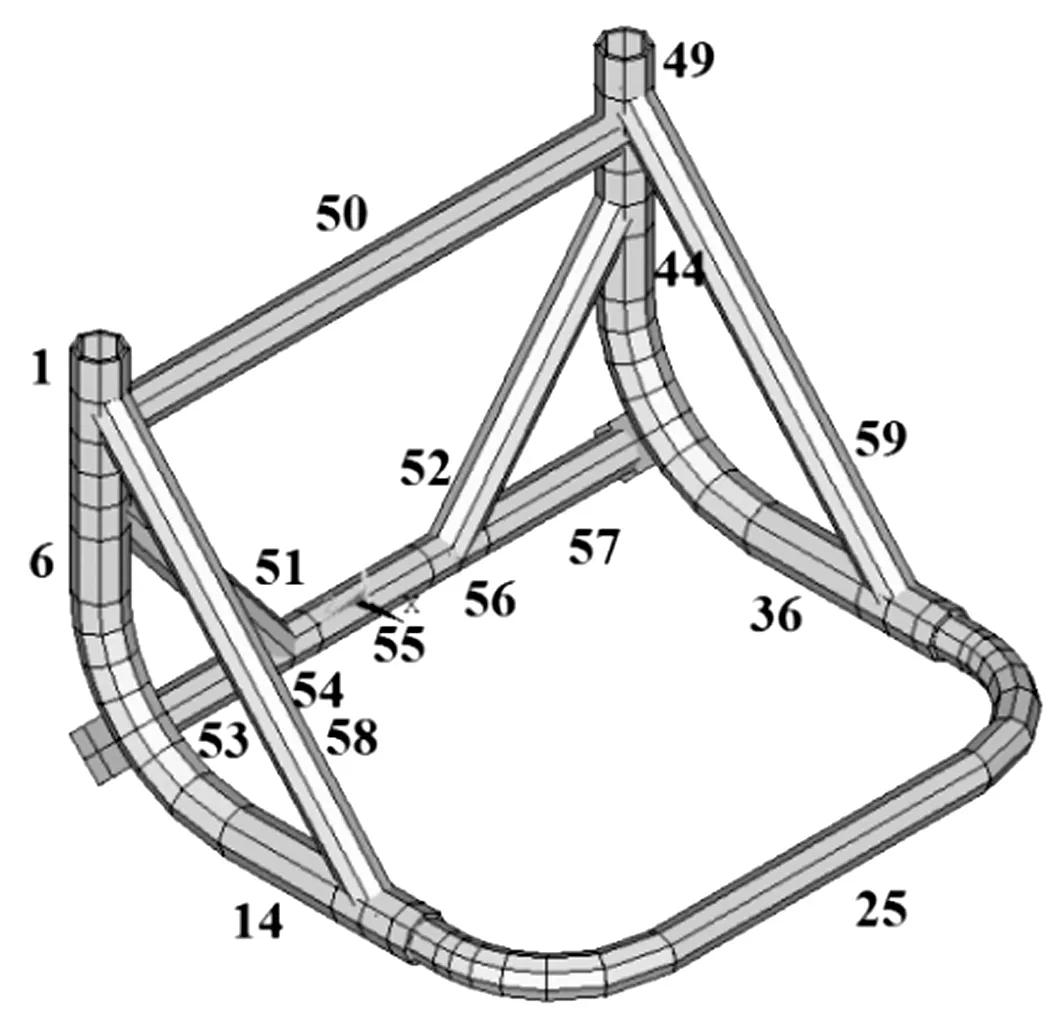
图2　发射台骨架结构有限元模型Fig.2　The finite element model of launch platform

通过拉丁超立方方法获得50组损伤样本，利用ANSYS软件计算各损伤样本对应的结构响应，以发射台损伤参数值为输入变量，结构模态频率和模态振型为输出变量，建立发射台骨架模型的Kriging代理模型，验证Kriging代理模型的准确性并依据加点准则进行修正，得到结构响应与损伤参数值之间的关系，即为修正后的发射台骨架Kriging代理模型。

得到发射台骨架的Kriging代理模型后，在发射台骨架模型上设置真实损伤进行损伤识别，损伤通过在发射台骨架第50号直管左侧1/4处锯裂缝的方式进行设置(见图3)，具体情况见表1。

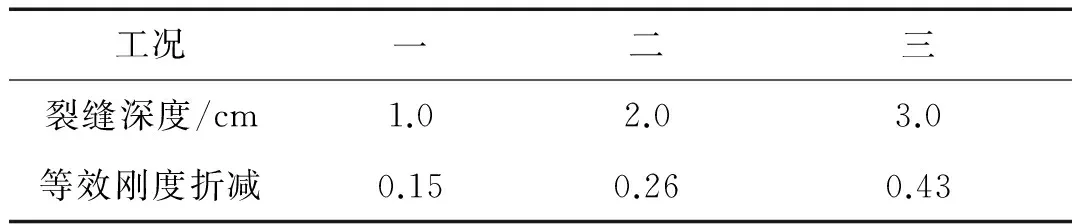
表1　损伤工况

为了表征损伤程度，通过有限元模型修正方法获得裂缝深度为1 cm，2 cm，3 cm时对应的结构损伤处刚度折减分别为15%，26%和43%。

图3　发射台骨架实验工况设置Fig.3　The damage condition arrangements of launch platform

试验时模型通过橡胶绳悬挂于刚架上，使其处于自由状态，在发射台骨架上通过力锤敲击的方式施加脉冲激励，使用江苏东华公司生产的DH5920动态信号测试分析仪及其配套软件对结构进行试验数据采集和模态分析，采样频率为10 kHz。然后利用建立好的Kriging代理模型，使用多族群粒子群优化算法进行优化识别，族群个数设为5，族群规模为20，搜索维度为10，搜索范围(0，1)，通过调整代理模型中的损伤参数值使目标函数取得最小值，得到对应的识别结果如表2。

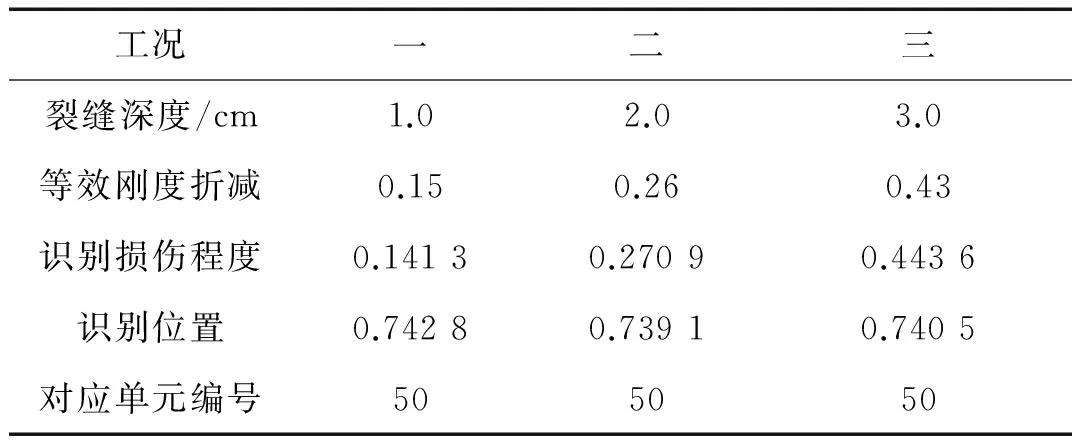
表2　损伤识别结果

由表2识别结果可知，通过Kriging代理模型可以确定结构损伤发生在第50号直管位置，并基本描述出结构损伤程度，但是损伤具体状况无法判断。下面给出结构前四阶固有频率与损伤参数值之间Kriging代理模型的响应面(见图4)：

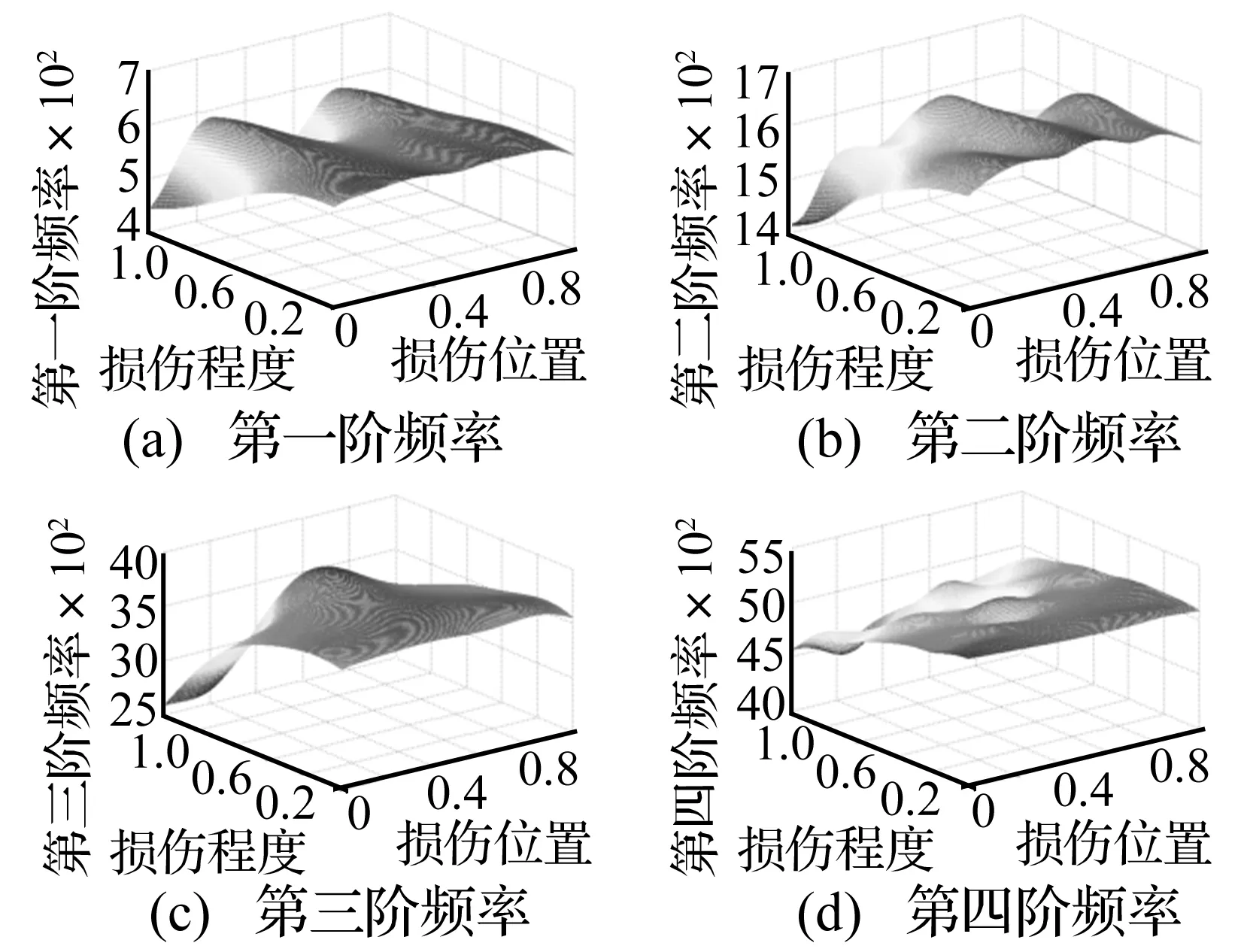
图4　前四阶模态频率Kriging代理模型响应面Fig.4　The Kriging surrogate model response surface of each frequency

2　基于MSECD的结构损伤识别

前文通过建立结构的Kriging代理模型，进行结构损伤定位研究，确定了结构损伤所在单元组，但无法对损伤具体状况进行判断。接下来，将以动力指纹方法为基础，以结构单元模态应变能曲率差为指标，进行结构损伤的精确识别，确定损伤的具体位置，并对结构损伤程度进行定性描述。

2.1理论基础

结构单元模态应变能是一个对结构局部损伤比较敏感的损伤识别指标，可以有效定位损伤单元[10]。将其与曲率工具相结合，不仅可以增加损伤识别方法对局部损伤的敏感性，同时能提高损伤识别的准确性。

2.1.1结构单元模态应变能

定义结构第j个单元的第i阶单元模态应变能(MSE)如下：

MSEij={φi}T[Kj]{φi}

(5)

由n自由度系统的固有振动方程

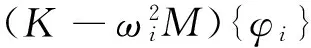
(6)

可得：

(7)

因此，对第j个单元有：

(8)

即结构第j个单元的第i阶模态应变能也可表示为：

(9)

2.1.2模态应变能曲率差指标

首先按照式(9)求出改进后结构损伤前后的单元模态应变能MSEu和MSEd，然后根据曲率的定义求出它们的曲率矩阵MSECu和MSECd如下：

(10)

(11)

式中：hj为第j单元的长度，当各个单元长度相同时，可以忽略。最后求出两个曲率矩阵的差值矩阵，记为：

(12)

2.2发射台骨架模型局部损伤识别试验

2.2.1试验设置

前文通过建立结构的Kriging代理模型，确定结构损伤位于第50号直管单元组，现对第50号直管单元组重新标号(见图5)，运用基于结构单元模态应变能曲率差的损伤识别方法对结构损伤进行局部识别。

图550号直管单元组重新标号情况
Fig.5Renumber of the 50 th element

结构实际损伤通过在图示50号直管左侧1/4处切口的方式进行模拟。具体情况见表1和图3。

试验时模型通过橡胶绳悬挂于刚架上，使其处于自由状态，采用锤击方式进行激励，使用江苏东华公司生产的DH5920动态信号测试分析仪及其配套的软件对结构进行数据采集和模态分析，共选择14个测点，传感器布置方案见图6，采样频率为10 kHz。

图6　传感器布置方案Fig.6　The arrangement of sensors

2.2.2试验结果分析

通过实验分析，得出结构前四阶模态频率和模态振型，由式(12)求得结构MSECD，以节点编号为横坐标，结构第三阶MSECD为纵坐标作图，得到试验结果见图7。

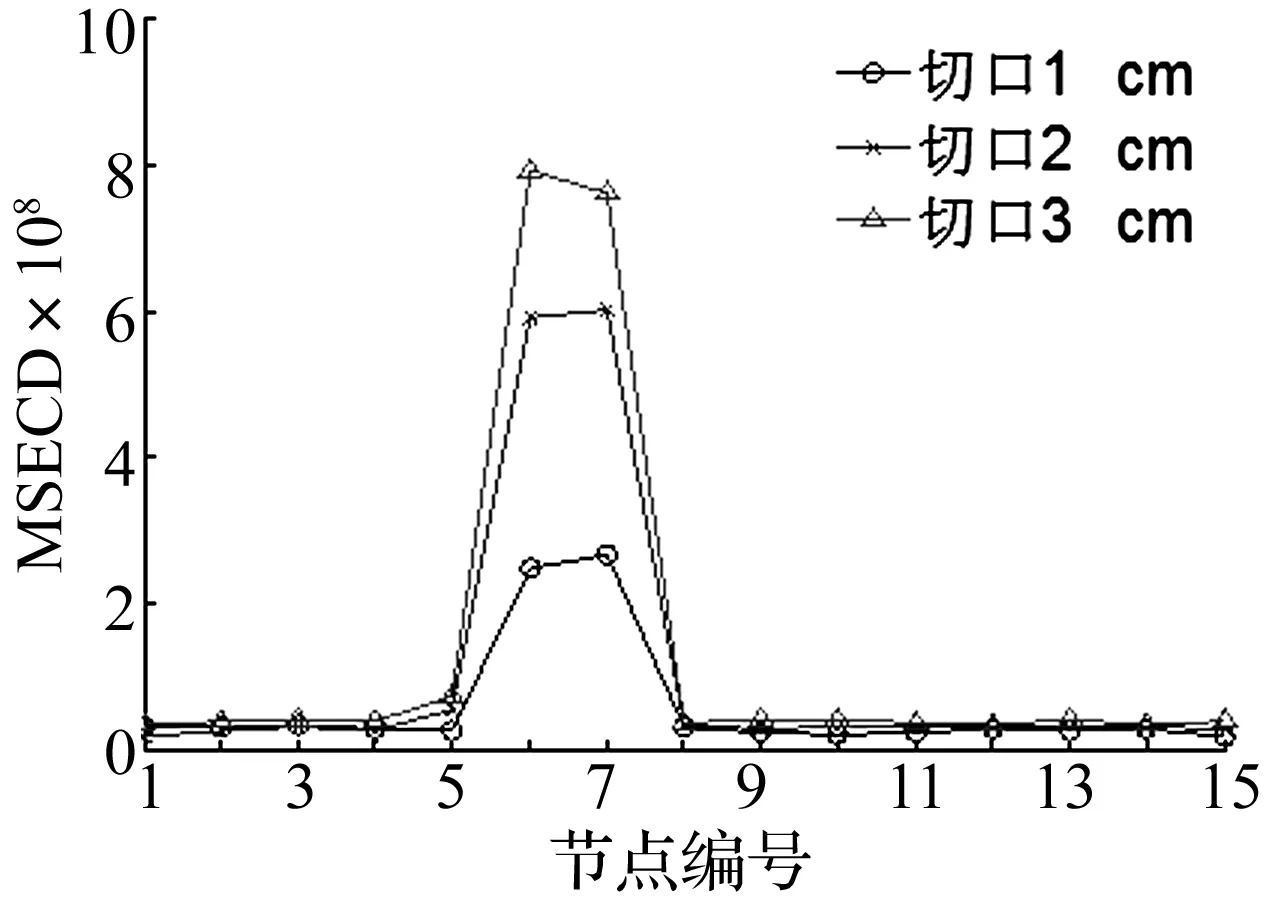
图7　损伤识别结果Fig.7　The results of damage identification

由图7可知，结构MSECD在节点6、节点7处发生明显峰值变化，证明6号单元发生损伤，且随着损伤程度的不同，结构MSECD变化有较明显区分。

3　结　论

本文提出了一种基于MSECD和Kriging代理模型的大型复杂结构损伤识别两步法：① 建立结构的Kriging代理模型，通过优化反演，确定结构损伤所在单元组；② 以动力指纹方法为基础，运用单元模态应变能曲率差方法对结构损伤进行局部识别，确定损伤具体状况。通过某发射台骨架模型的试验研究，证明了本文所提损伤识别两步法可以有效确定大型复杂结构损伤状况，为大型复杂结构的损伤识别问题提供了一种新的思路。

[1] 郭利, 张瑞刚, 李永军,等. 基于模态柔度曲率差的弯管结构损伤识别.[J]. 振动、测试与诊断,2013,33(9):902-906.

GUO Li, ZHANG Ruigang, LI Yongjun, et al.Damage identification of bend-type structure based on modal flexibility-curvature and difference[J]. Journal of Vibration,Measurement & Diagnosis, 2013,33(9):902-906.

[2] 傅奕臻, 魏子天, 吕中荣,等. 基于时域响应灵敏度分析的板结构损伤识别[J].振动与冲击,2015,34(4):117-120.

FU Yizhen, WEI Zitian, LÜ Zhongrong, et al. Damage identification of a plate based on response sensitivity analysis in time domain[J]. Journal of Vibration and Shock,2015,34(4):117-120.

[3] 王利英, 杨绍普, 赵卫国. 基于改进布谷鸟搜索算法的架桥机结构损伤识别[J]. 北京交通大学学报, 2013,37(4):168-173.

WANG Liying, YANG Shaopu, ZHAO Weiguo.Structural damage identification of bridge erecting machine based on improved Cuckoo search algorithm[J]. Journal of Beijing Jiaotong University, 2013,37(4):168-173.

[4] 李世龙, 王天辉, 马立元,等.大型复杂结构损伤识别两步法研究[J].中国机械工程, 2012,23(9):1051-1055.

LI Shilong, WANG Tianhui, MA Liyuan, et al. Study on two-step damage detection methods of large complex structures[J]. China Mechanical Engineering, 2012,23(9):1051-1055.

[5] 祁荣宾,何镓梁,靳文浩,等.基于Kriging代理模型的PX氧化过程优化[J]. 华东理工大学学报(自然科学版), 2012,38(6):712-716.

QI Rongbin, HE Jialiang, JIN Wenhao, et al. PX oxidation process optimization based on kriging surrogate model[J]. Journal of East China University of Science and Technology(Natural Science Edition), 2012,38(6):712-716.

[6] 邢红星,琚太忠,林建阳.普通克里格法在矿产储量计算中的应用[J]. 地质与勘探, 1997(4):46-51.

XIN Hongxing, JU Taizhong, LIN Jianyong. The ordinary Kriging’s application to mineral calculation of reserves[J]. Geology and Prospecting, 1997(4):46-51.

[7] 肖立峰,张广泉,张以都. 基于Kriging代理模型的结构形状优化方法[J]. 机械设计, 2009,26(7):57-60.

XIAO Lifeng, ZHANG Guangquan, ZHANG Yidu. Optimization method of structural shape based on Kriging surrogate model[J]. Journal of Machine Design,2009,26(7):57-60.

[8] 陈永亮,刘双,王汉涛,等.基于Kriging代理模型的主轴箱稳健设计[J]. 天津大学学报,2011,44(12):1111-1117.

CHEN Yongliang, LIU Shuang, WANG Hantao, et al. Robust design of headstock based on Kriging surrogate model[J]. Journal of Tianjin University, 2011,44(12):1111-1117.

[9] 于开平, 刘荣贺.多族群粒子群优化算法飞行器结构模型修正[J].振动与冲击, 2013,32(17):79-83.

YU Kaiping, LIU Ronghe. Model updating of a spacecraft structure based on MRPSO[J]. Journal of Vibration and Shock, 2013,32(17):79-83.

[10] 史治宇, 罗绍湘, 张令弥.结构破损定位的单元模态应变能变化率法[J]. 振动工程学报, 1998,11(3): 356-360.

SHI Zhiyu, LUO Shaoxiang, ZHANG Lingmi. Determination of structural damage location based on elemental modal strain energy change[J]. Journal of Vibration Engineering, 1998,11(3): 356-360.

[11] 孟海平,蔺新艳,杨健辉.结构破损定位中模态应变能法的改进[J].广西大学学报(自然科学版),2013,38(1):23-27.

MENG Haiping, LIN Xinyan, YANG Jianhui. Improvement of structural damage localization based on modal strain energy method[J]. Journal of Guangxi University(Natural Science Edition),2013,38(1): 23-27.

New damage identification method for large complex steel tube welded structure

GUO Junlong, MA Liyuan, LI Yongjun, WANG Tianhui

(Department of Missile Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

A new two-step method for large complex structure damage identifications was proposed by combining the Kriging surrogate model with the dynamic fingerprints. The Kriging surrogate model between the dynamic response and the damage parameters was established, instead of the former finite element model, to locate globally the damage. Then, taking the modal strain energy curvature difference as an index, the structure damage was locally identified and the damage status was confirmed by the dynamic fingerprint method. The two-step identification method was applied in the damage identification of a missile launch platform model. The results indicate that the method could be applied in practical projects, providing a new idea for the damage identification of large complex structure.

large complex structure; damage identification; Kriging surrogate model; modal strain energy curvature difference

2015-07-21修改稿收到日期：2015-09-17

郭俊龙 男，硕士生，1990年生

马立元 男，教授，博士生导师，1962年生

TU311

A DOI:10.13465/j.cnki.jvs.2016.14.030