RV减速器偏心轴随动磨床的加工精度分析

范晋伟，张兰清，王鸿亮，袁　帅

（北京工业大学 机械工程与应用电子技术学院，北京 100124）

RV减速器偏心轴随动磨床的加工精度分析

范晋伟，张兰清，王鸿亮，袁帅

（北京工业大学 机械工程与应用电子技术学院，北京 100124）

偏心轴随动磨床是加工偏心轴工艺链中最核心的设备，磨削过程中C-X轴随动磨削运动模型的建立及运动关系的确定直接影响到磨削加工质量的优劣，且在磨削过程中存在着诸多误差影响因素，分析这些因素对工件质量的影响规律非常重要，主要通过X坐标位置变化、头架转动变化、砂轮中心偏心变化在加工过程中误差产生的机理，建立几何关系进行求解，并进行MATLAB仿真，找出误差来源，为后续误差补偿做铺垫，以达到提高加工精度的目的。

偏心轴；加工精度；随动磨削；几何关系；RV减速器

0　引言

随着智能化制造业的来临，如今工业机器人开始逐渐运用于各个领域，其发展质量和水平很大程度上代表一个国家的工业发达水平［1］。偏心轴作为工业机器人关节处RV减速器中的核心部件［2］如图1所示，一般用于低速或静止调节位置，要求体积小，加工精度高。因此其加工质量和加工效率直接制约着工业机器人的发展。RV减速器偏心轴随动磨床是磨削偏心轴的工作母机，对其自身的精度要求更高，然而磨床自身的磨损和人为因素误差影响远远高于零件表面粗糙度误差的影响，成为影响整体零件的加工质量的主要因素，所以必须采取有效措施加以解决［3］。

图1　RV减速器偏心轴三维模图

早期天津大学的刘又午等提出了基于多体系统理论的数控机床运动空间误差模型，提出用9线法对位移误差进行辨识，并在一台数控加工中心进行软件误差补偿实验［4］。2002年国防科学技术大学粟时平［5］以多体系统理论为基础建立了多轴数控机床的通用精度模型。2003年，上海交通大学杨建国等基于齐次坐标变换理论建立了空间误差模型［6］。2009年，杨程旭等［7］基于多体系统理论，阐述了四轴运动平台综合空间误差的建模过程。而我国现如今针对随动式RV减速器偏心轴的磨床研究还很少，但最近北京第二机床厂初有成效，生产了一套整机设备，机床整体技术达到国际领先技术水平，但在加工精度上还需进一步有效提高。在机械加工中，机床加工的尺寸精度最终是由机床上刀具与工件之间的相对位移决定的［5］。一般来言，机械加工过程中存在的误差可以分为两类：系统误差和随机误差［8］。图2针对随动性数控磨削机床在加工过程中存在的误差进行统一归纳，在不考虑热传动及变形误差的前提下，对随动数控磨削误差进行分析。随机误差的出现可以通过数理统计进行分析，适当的加以改进［9］。对于常值系统误差，在分析其误差的大小及方向性质后，通过调整或检修的方法来人为反向加以抵消。对变值系统误差可以通过连续或定期性的补偿进行修正。周志雄［10］教授分析了随动磨削运动的刚度误差，但没能用于实际的生产当中。本文通过归纳总结磨床在加工过程中的误差来源，并从X坐标位置变化、头架转动变化、砂轮中心偏心变化在加工过程中误差产生的机理，建立几何关系进行求解，并进行MATLAB仿真，找出误差来源，为误差补偿做铺垫，并应用于实践生产之中。

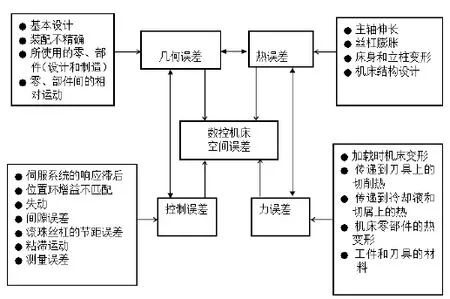
图2　随动磨床误差源分析

1　砂轮安装偏心引起的误差

偏心轴偏轴在磨削过程中，砂轮架往复大行程运动，且磨削切点的位置始终变化，所以有必要对砂轮初始安装时的偏心误差进行分析，获得其对工件表面质量的影响情况。

砂轮中心实际安装位置与理想位置的偏差在平面内任何方向都可能产生，且大小不定，这里随机假定一个误差大小为HΔ的偏差矢量，然后分析该矢量在整周内对磨削精度的影响。如图3所示。

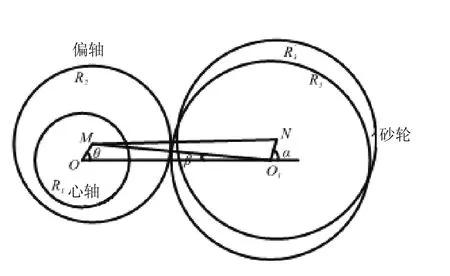
图3　砂轮安装偏心误差形成机理

图示中，O1为砂轮的理想安装位置，O1N为任意偏心矢量，它与水平正方向的夹角为α，N点为砂轮中心的偏心位置。分析几何关系知：

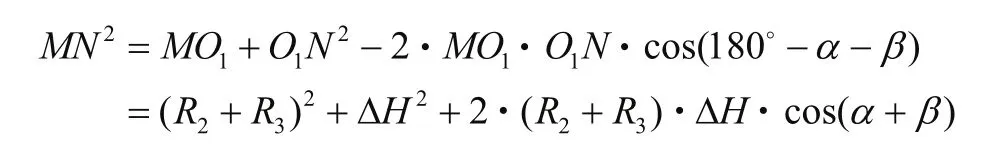
式中：

理论磨削点与偏心状态下引起的位置误差为 eΔ，则：

把式（1）代入式（2）得：

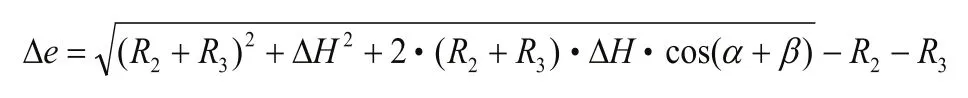
按即定参数 ，且砂轮中心偏心矢量长度为0.02mm时，旋转范围为内，工件旋转一周过程中，根据上式，利用计算机仿真，得到偏轴误差图4。

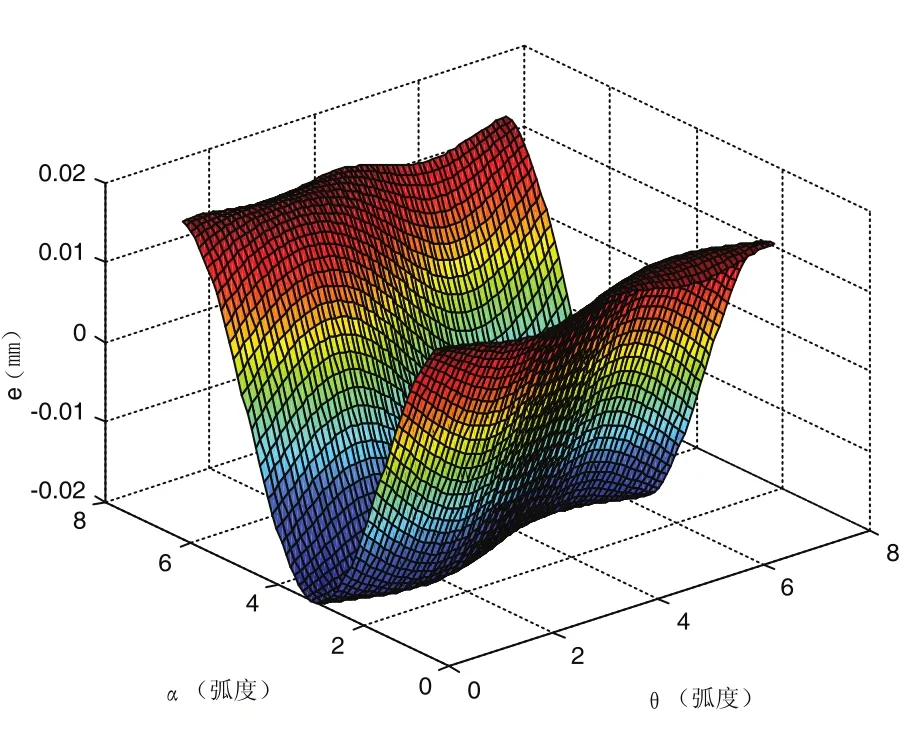
图4　砂轮安装误差与加工误差关系图

分别取图4中，偏心角度为0°、90°、180°、270°几个特殊位置的偏轴加工二维误差图像，并取其最大与最小误差值，且在偏心长度条件下，如图5所示。

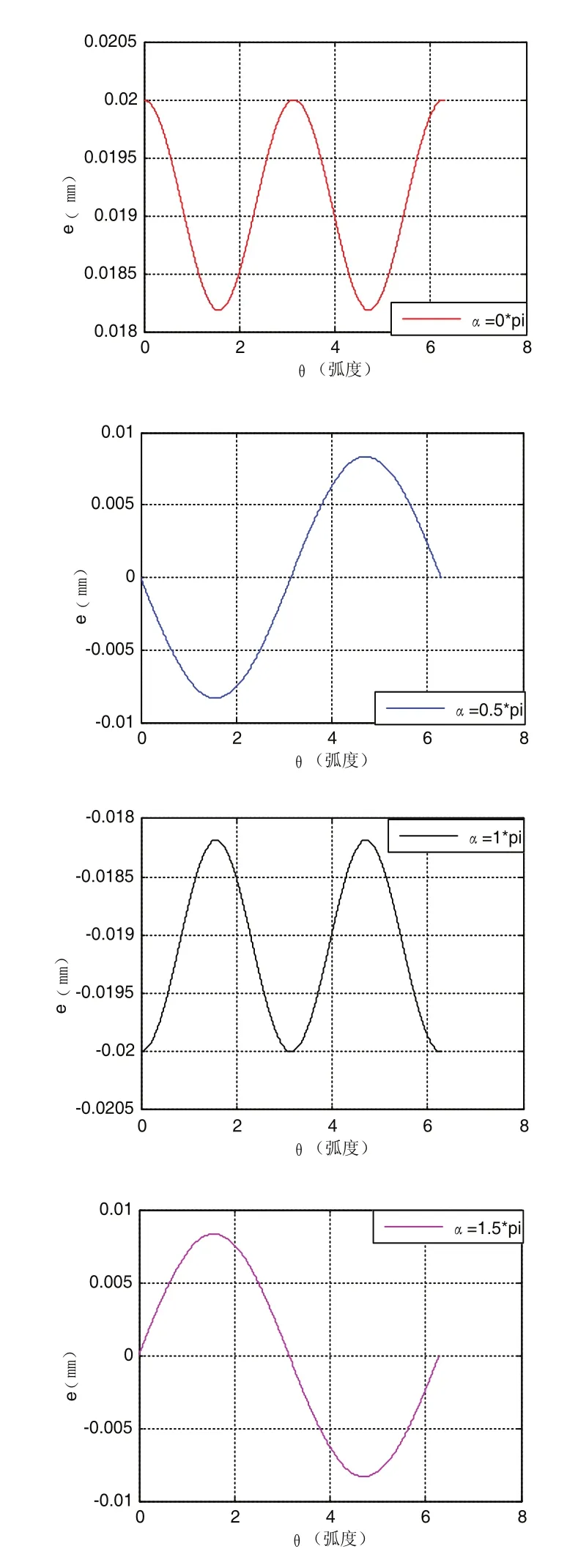
图5　加工误差图

利用计算机提取出在几个特殊位置处的误差值发现，在水平位置（即0°与180°处），取相等的偏心长度值，在垂直位置（即90°与 270°处），由此可以得出结论，当砂轮偏心位置处于水平方向时，对偏轴的误差影响较明显，当砂轮处于垂直方向位置时，对其影响较小。

2　X坐标轴的位置变化引起的误差

砂轮架带动砂轮跟随主轴旋转作往复运动，在大行程的运动范围内，机床导轨或电机伺服原因会导致砂轮中心在X坐标轴的位置与理想位置的偏离，引起偏轴轮廓误差。当X的实际位置滞后 xΔ时，其误差形成机理如图6所示。

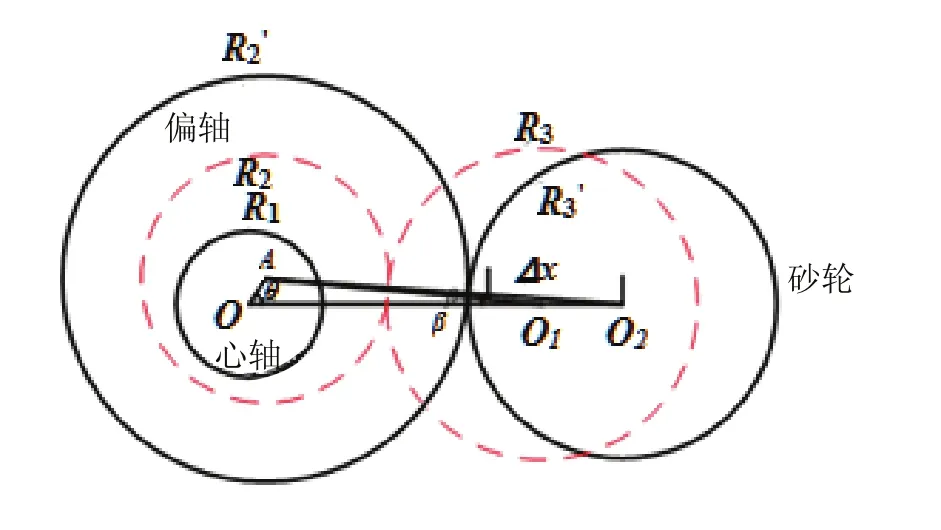
图6　X坐标轴的位置变化引起的误差形成机理

在三角形AO1O2中，由余弦定理知：

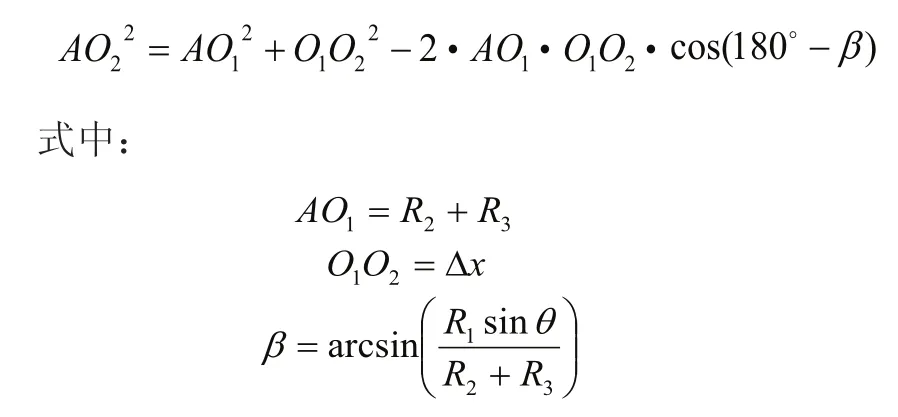
因砂轮中心滞后而产生的偏轴加工误差记为e，则：

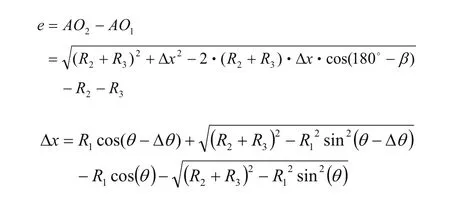
式中，Δθ为与砂轮中心Δx 对应的曲轴转角变化量。

当R1=200（mm），R2=80（mm），R3=400（mm），且取砂轮中心滞后的偏心轴转角变化量Δθ 为0.05°、0.1°时，偏轴误差在工件旋转一周内的仿真图如图7所示。

由图7知，曲线1、2分别代表砂轮中心滞后导致的偏心轴转角变化量Δθ 为0.05°、0.1°时，偏轴加工误差随心轴转角的变化曲线；当Δθ=0.05°时，最大误差值为0.1745mm，且处在偏心轴转角为90°与270°位置处；当Δθ=0.1°时，最大误差值为0.3491mm，也在偏心轴转角为90°与270°位置处；由此可以看出，曲轴旋转过程中，X坐标位置的变化在0°与180°对偏轴误差影响最小，在90°与270°位置影响最大。

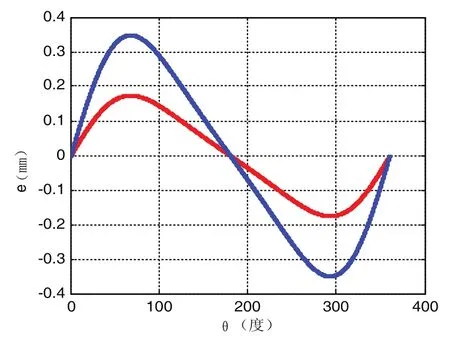
图7　X坐标滞后误差与加工误差关系

同理可分析X坐标位置超前时的误差影响情况：

图8为砂轮坐标X超前于理想加工坐标时的误差产生机理，偏轴加工误差e的表达式如下：

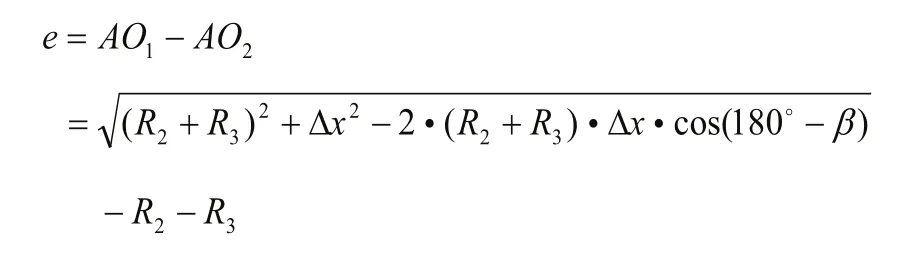
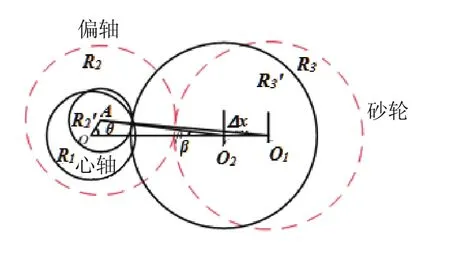
图8　X坐标超前加工误差产生机理

代入上述的假定偏心轴尺寸，在偏心轴旋转一周的范围之内，取因砂轮中心超前引起的曲轴转角变化量为0.05度、0.1°，对偏心轴加工误差进行仿真，如图9所示。

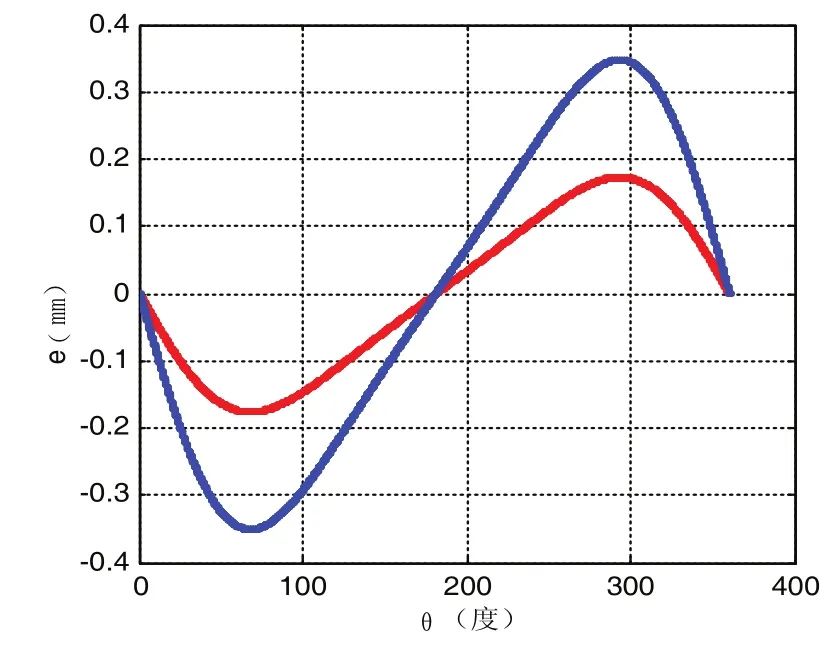
图9　X坐标超前误差与加工误差关系

由图可知，砂轮中心超前于理想位置时，引起的连杆颈误差在90°与270°处为最大，0°与180°处为最小。

综上所述，砂轮中心X坐标的位置变化将会直接影响连杆颈加工后的几何尺寸，且在影响位置最显著的90°与270°处，误差方向相反，会导致连杆颈的圆度偏差。

3　头架转动位置误差变化引起的误差

偏心轴随动磨削的过程中，主轴头架的旋转与砂轮架的往复运动是为了保证砂轮磨削点与工件的加工点相切运动关系。从相对运动关系分析，头架转动较快就相当于砂轮架移动较慢，反之亦然。所以，头架转动滞后产生的误差影响规律与X坐标位置滞后相反，即在整周运动中，在0°～180°时，误差影响最大，在90°和270°时，误差影响最小。

4　结论

本文总结归纳了随动磨削机床的误差来源分析，重点介绍了X坐标位置变化、头架转动变化、砂轮中心偏心变化在加工过程中误差产生的机理，通过进行几何建模分析，运用MATLAB仿真，直观的再现了误差的影响情况，为误差补偿奠定基础，并找出了主要以下误差来源：1）砂轮偏心位置处于水平方向时，对连杆颈的误差影响较明显；2）砂轮中心X坐标的位置变化将会直接影响连杆颈加工后的几何尺寸，且在影响位置最显著的90°与270°处，误差方向相反，会导致连杆颈的圆度偏差；3）头架转动滞后产生的误差影响在整周运动中，在0°～180°时，误差影响最大。其结果对以后投入实践生产，开发出特定的偏心轴磨床误差补偿技方法，提高加工偏心轴的生产质量和效率提供了必要的条件。

［1］ 王庆明.先进制造技术导论［M］.华东化工学院出版社，2007.

［2］ 范晋伟，宁堃.提高曲轴磨削精度的几何误差补偿技术［M］.机械设计与制造，2012.

［3］ 陆岩.机器人用RV减速器传动误差研究与分析［D］.大连交通大学.2013:1-50.

［4］ 刘又午，刘丽冰，赵小松，章青，王树新.数控机床误差补偿技术研究［J］.中国机械工程，1998，9（12）:48-51.

［5］ 粟时平.多轴数控机床精度建模与误差补偿方法研究［D］.长沙:国防科学技术大学，2002.

［6］ 任永强，杨建国.五轴数控机床综合误差补偿解耦研究［J］.机械工程学报，2004，40（2）:55-59.

［7］ 杨程旭，郑煜，徐洲龙.多体系统理论的四轴运动平台综合空间误差建模［J］.现代制造工程，2009，（4）:1-4.

［8］ 许第洪，孙宗禹，周志雄，陶剑波，罗红平.切点跟踪磨削法加工误差分析［J］.机械工程学报，2003，39（12）:103-108.

［9］ 粟时平.多轴数控机床精度建模与误差补偿方法研究［D］.长沙:国防科学技术大学，2002.

［10］ 周志雄，罗红平，许第洪，孙宗禹，宓海青.切点跟踪磨削法中工件的刚度误差分析及其补偿［J］.机械工程学报，2003，39（6）:98-101.

Machining precision analysis of follower grinder with RV reducer eccentric axis

FAN Jin-wei，ZHANG Lan-qing，WANG Hong-liang，YUAN Shuai

TH114；TG659

A

1009-0134（2016）09-0084-04

2016-07-08

国家科技重大专项（2013ZX04011013）；国家自然科学基金项目（51275014）

范晋伟（1965 -），男，河南西平人，教授，博士，研究方向为数控磨床可靠性与超精密加工。