重组练习材料 提升思维品质
陈瑾

教学人教版五年级上册《三角形的面积》之后,我发现教材中的练习题大多是利用面积计算公式,直接求面积,或者求高或底,而这些都是学生早就熟练掌握的内容。那么,在基础性学力之外,发展性学力、创造性学力如何兼顾?
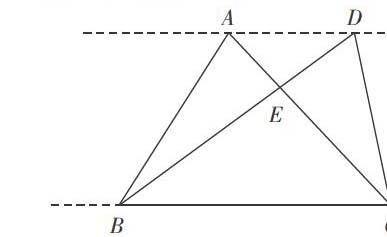
教材安排了一道练习题,在两条平行线中寻找面积相等的三角形(见下图),并画出与原三角形面积相等的三角形(见下图)。这道题背后隐藏的“等积变形”思想是图形与几何领域的重要思想方法之一,也是初中学习几何证明时常用的方法。因此,我充分利用这道题,在材料重组方面下功夫,引导学生体会等积变形的思想方法,培养空间观念,达到提升思维品质的目的。
一、经历分层探究的过程,拓宽思维的广度
关注学生的学习基础与学习能力,创设简洁的情境,一题多变,促使学生在灵活运用三角形面积计算公式的基础上分层探究,在直观感受与动手操作中进一步理解“等底等高,面积相等”的含义,真正弄清知识的来龙去脉。
【案例1】在方格纸中分别以下面直角三角形的BC、AB、AC三条边为底,画出与它面积相等的三角形。(见图1)
环节一:以直角三角形的BC边为底,画出与它面积相等的三角形。(见图2)。
反馈:先选择学生的作品展示,再引导学生理解:这些三角形的形状完全不同,但是等底等高,所以面积肯定相等。
师:像这样的三角形还能画吗?你能快速找到它们吗?
生:我画一条与BC平行的平行线,可以很快找到无数个这样的三角形。
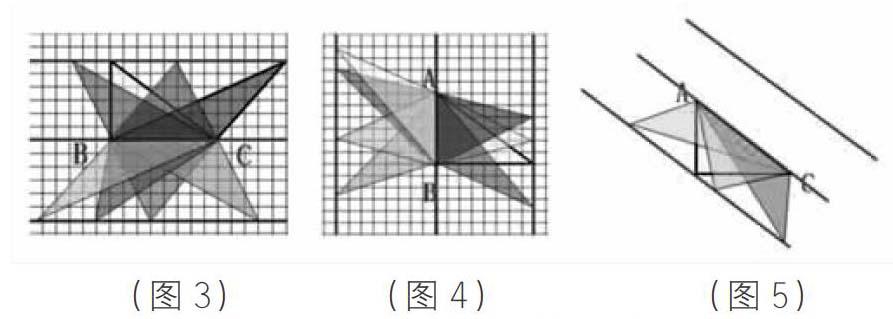
再引导学生发现平行线可以朝上画,也可以朝下画,所以这样的三角形有无数个。随后课件演示。(见图3)
师:因为这些三角形等底等高,所以面积肯定相等。即使形状千变万化,但是面积始终不变,这就是我们在数学学习中通常说到的“等积变形”。
环节二:请在头脑中想象,以直角边AB为底,画出与原三角形面积相等的三角形。学生先独立思考,教师再用课件演示以AB为底的画法。(见图4)
环节三:出示一幅没有方格的图,学生以斜边AC为底,画出与原三角形面积相等的三角形。
先反馈学生作品,再演示课件上的画法,接着教师再用电子白板演示在平行线上拉动三角形顶点,形状改变但面积不变的过程。(见图5)
小结:不管平行线是横向还是纵向,或者是斜向的,只要三角形的一条边在平行线上,对应顶点在另一条平行线的任意位置,所形成的无数个三角形都和原三角形面积相等,因为它们既等底又等高。
同一素材一变再变,三个环节环环相扣,在充分感受“等底等高,面积相等”的基础上,将思维提升到“等积变形”的高度,把刚才的探究过程整理如下表:
二、体验多样的解题策略,提升思维的灵活度
“为班级学习共同体提供有一定难度的问题”是集体学习材料理想的标准,无论是苏联的赞科夫还是日本的佐藤学,都是同样的观点。先让学生充分地自主尝试,然后互相交流,互通有无,体验多样的解题策略,真正学有所得,从而提升思维的灵活度。
【案例2】求出下面阴影部分的面积。
方法1:用大面积减小面积的方法做。先求大梯形的面积,再减去空白部分三角形的面积,得到的就是阴影部分的面积即32平方厘米。
方法2:因为两个阴影部分的三角形等高,所以可以把左边阴影部分三角形变形,移动顶点和右边的三角形拼在一起,组成一个规则的大三角形,底是16厘米,高是4厘米,所以面积是32平方厘米。
然后教师引导一名学生用电子白板演示拉动顶点等积变形的过程。学生认真观察,纷纷笑眯眯地点头,表示和自己想的一样。(见图7)
师:还可以怎么变?
方法3:把右边的三角形往左拉,也可以拼成一个底是16厘米、高是4厘米的大三角形,两种方法本质上是相同的。(见图8)
方法4:既然可以往左拉,往右拉,那么肯定可以从两边同时往中间拉。平行线上有无数个点,所以就有无数种拉的方法。(见图9)
师:同学们的脑子真灵活呀,真是一点就通!(伸出大拇指表示赞赏)
当学生在经历“山重水复疑无路”的无奈之后,在对比和碰撞中打破思维平衡,在解决具体问题的过程中体验策略多样化,并感悟“等积变形”方法的便捷性,最终收获“柳暗花明又一村”的喜悦。
【案例3】求出不规则四边形的面积。(见下图10)
方法1:添加几条线,补出一个大长方形,就能很明显看出两个三角形的面积之和就是这个长方形面积的一半,所以直接用长方形面积除以2。(见图11)
方法2:假设上下两个三角形的高分别是h1和h2,求总面积用6h1÷2+6h2÷2,可用乘法分配律变形为(6h1+6h2)÷2,再到6(h1+h2)÷2,最后得到6×9÷2,结果也是27平方厘米。(见图12)
方法3:用等积变形的方法,把上面三角形的顶点平行拉动到右边,直到把两个三角形变成一个规则的大三角形为止。求总面积仍然用6×9÷2,结果还是27平方厘米。(见图13)
同学每介绍一种做法,老师都真诚赞扬,其他同学也报以热烈的掌声。
小结:三个同学,三种思路,都可以用算式6×9÷2来解决,相比较而言,我们通过移动顶点,运用等积变形的方法来做(见图13),显然更加简单。
这两道习题的设计是经过深思熟虑的,既可以用常规方法来做,又能利用转化思想,用“等积变形”的方法来解决,策略选择的多样化能满足不同层次的学生的需求。
三、提供富有张力的材料,挖掘思维的深度
数学教学要适当追求学生对知识理解的深刻性,教师要善于捕捉与寻找复杂的、有张力的、有丰富内涵的关系,使教学材料呈现丰富的结构,从而促使学生的思维更有深度。
【案例4】下图是由边长分别为5厘米和4厘米的两个正方形组成,求阴影部分的面积。
方法1:用两个大正方形的总面积减去空白部分,也就是三个小三角形的面积,就得到阴影部分的面积。
师:同学们用常规方法——大面积减去小面积来做,很好!但是,解决这道题还有更加巧妙的方法,我们是否可以从等积变形的角度思考呢?
学生独立思考,然后交流。
方法2:我把阴影部分看成两个小三角形,分别等积变形,可以变成一个底和高都是4厘米的大三角形BEF,面积是8平方厘米。(见图14)
师:非常棒,真是奇思妙想!(大家纷纷为这位同学献上热烈的掌声。)
师:还有别的想法吗?如果没有,老师给个提示(课件出示平行线),同学们再尝试解决。
方法3:以阴影部分三角形的一条边为底,将它对应的顶点在这组平行线之间移动,移到它变成一个直角三角形为止。这个直角三角CEG形恰好是小正方形面积的一半,所以面积就是4×4÷2=8平方厘米。(见图15)
有的同学还在思考,有的同学一下就看明白了,发出一声惊呼。老师再借助电子白板,动态呈现在一组平行线之间移动三角形顶点等积变形的过程,这时更多学生露出会心的笑容。接下来,同桌之间对这道题如何采用等积变形的方法再次讨论,交流。
师:你能像刚才这样,在这幅图再创造出两个面积相等的三角形吗?试一试吧。(见图16)
在数学学习中,教的立足点是促进学生的学。从学生实际出发,通过教材重组,提供合适难度的练习,渗透数学思想方法,是培养学生思维不可或缺的要素,也是提高学生数学素养不可忽视的途径。
(作者单位: 浙江省杭州市文海实验学校)
责任编辑 曾维平
E-mail:25365420@qq.com

