粒子群优化SVM在气体定量分析中的应用

郑尧军，陈红岩，冯　勇，陈开考，曲　健

（1.浙江经济职业技术学院汽车技术学院，杭州310018；2.中国计量学院机电工程学院，杭州310018）

粒子群优化SVM在气体定量分析中的应用

郑尧军1*，陈红岩2，冯勇1，陈开考1，曲健2

（1.浙江经济职业技术学院汽车技术学院，杭州310018；2.中国计量学院机电工程学院，杭州310018）

针对机动车尾气排放CO气体的定量分析中，支持向量机建模的参数难以确定、光谱数据计算量过大等问题，提出了一种自适应变异粒子群优化的支持向量机方法，对浓度范围在0.5%～8%的20组不同浓度的CO气体进行定量分析。通过对汽车尾气中CO气体的初始数据进行优化，再将优化的核函数带入支持向量机进行浓度的回归分析，将结果与BP神经网络模型回归效果作对比，实验表明：粒子群寻优得到的最优参数c=39.315 2，g=0.178 55；BP神经网络的适应度值在迭代60次之后趋于稳定，SVM建模时间约为BP网络的1/30，且SVM预测精度明显高于BP网络。相比与BP网络，SVM更适合处理气体定量分析问题。

传感器应用；支持向量机；粒子群优化；BP神经网络；遗传算法

EEACC:7230；B40；4145doi:10.3969/j.issn.1004-1699.2016.07.028

目前，气体的定量检测已广泛应用于食品安全、环境监测、生产安全等多个领域［1］。CO是有毒气体，过量排放将严重影响我们的身心健康。在CO气体定量分析方法中，主要采用红外吸收法，但由于传感器元器件的老化、温度的变化、供电电压的波动等因素，导致测量的精度不是很高，无法对汽车尾气排放进行有效的检测和监督。

提高气体测量精度的方法主要有人工神经网络［2-3］ANN（Artificial Neural Network）方法和支持向量机［4-6］SVM（Support Vector Machine）方法等。其中，余大洲［2］等人针对气体检测领域数据量巨大的特点，提出了使用RBF神经网络技术来实现对气体传感器阵列采集到的信息融合，并论证了该方法的可行性；王智文［7］等针对混合气体分析中建模时间过长以及泛化能力较差的问题，将主成分提取与贝叶斯正则化结合，对神经网络进行优化，使得建模时间从4 250 s降为8 s；曲健［8］等利用改进的网格搜索法对支持向量机进行参数优化，并应用于CO2气体定量分析中，得到了最优参数组合，进一步提高了预测精度；李玉军［9］等人将粒子群优化与最小支持二乘向量机相结合，建立混合气体定量分析模型，寻优时间节省 40倍以上；Manouchehrian Amin［10］等运用基于遗传算法寻优方法的支持向量机，建立回归模型，预测岩石的强度和可变性属性；

本文以SVM为基础对浓度范围在0.5%～8%的20组CO气体样本进行定量分析，选取其中15组样本作为训练集，选择剩余的5组气体样本作为验证集，验证模型的预测精度和水平。在SVM参数的选取问题上，提出了自适应变异粒子群优化算法。在20组气体样本的处理上，还采用了神经网络建模分析，并将SVM建模分析效果与遗传算法优化的BP神经网络建模相比较。

1　自适应变异粒子群优化

粒子群优化算法［11-12］PSO（Particle Swarm Optimization）是计算智能领域，除蚁群算法、鱼群算法之外的一种群体智能的优化算法。

在迭代过程中，粒子经个体极值和全局极值更新自己的速度和位置，公式为：

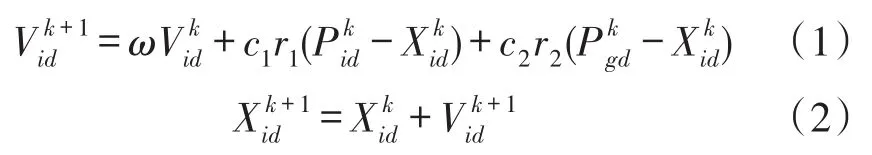
式中，ω为惯性权重；d=1，2，…，D，表示维数；k为当前迭代数；Vid为粒子速度；Xid为粒子位置；Pid为个体极值；Pgd为种群极值；c1和c2为加速度因子。粒子群优化算法收敛快，但存在着容易早熟收敛、搜索精度较低、后期迭代效率不高等缺点。因此，本文提出了自适应变异［13-14］的粒子群优化算法，指通过一定的准则和判定条件对相应的粒子采取变异操作，产生新的粒子，引导种群向最优解方向收敛。

2　遗传算法优化BP网络

遗传算法［15］是模拟自然界生物进化论和遗传机制而成的一种并行随机搜索的优化方法。遗传算法优化BP神经网络［16］流程如图1所示。

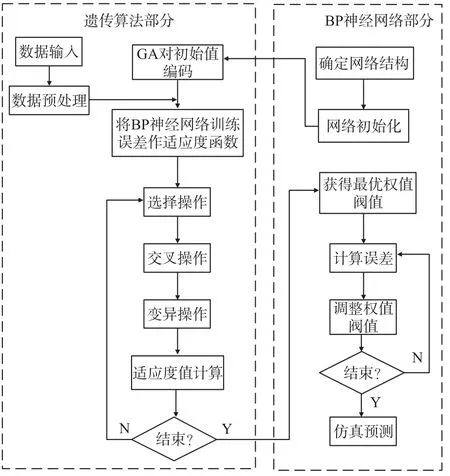
图1　遗传算法优化BP神经网络算法流程图

将预测输出与期望输出之间误差绝对值的和作为适应度值，计算公式为：

式中，yi为第i个节点的预测输出，oi为期望输出，n为输出节点数。

每个个体被选择的概率pi为：

其中，fi=k/Fi，Fi为个体i的适应度值，N为种群个体的数目。

交叉操作。例如第m个染色体am与第n个染色体an在l位进行交叉，则

式中，b为（0-1）之间的随机小数。

以第m个个体的第i个染色体ami为例，变异的操作表示为：

式中，amax为ami的上限，amin为ami的下限；f（g）= r2（1-g/G）2；r2为随机数，g为当前的迭代次数，G为设定的迭代次数；r为（0-1）之间的随机小数。

3　实验与分析

本实验采用不分光红外法（NDIR）对CO浓度进行检测。经过MCU调制的红外光源通过一定长度的气室内，气室中充有待测浓度的CO气体。由于CO对红外线波段中特征波长红外线能量的吸收，特定波长的光源通过气体后，在相应谱线处会发生光强的衰减，红外线的能量将减少，探测器检测剩余的光强度并转化为电信号，放大滤波后作为模型的输入。整个测试系统的原理如图2所示。

图2　NDIR测试系统原理图

图2中，检测系统的核心部件—传感器，包括进气口、出气口、红外光源、气室、探测器和信号处理电路等部分。

红外光源和探测器的优劣，将影响整个系统的检测精度。红外光源要求辐射的光谱成分稳定、辐射能量集中在待测分析组分气体特征吸收波段范围内、红外线应平行于气室的中心轴。探测器选用PerkinElmer公司生产的TPS4339热电堆探测器，具有对红外辐射产生温度变化的响应度高、信号处理能力强、分辨率和灵敏度较高等优点，能够满足对气体检测的需要。

3.1粒子群优化SVM建模分析

以标准浓度在0.5%～8%之间的20组CO气体作为实验样气，对标准浓度进行归一化处理，便是模型的期望输出。0.5%～8%之间的标准浓度是经过专业气体配置公司标准化配置的，所以可以保证标准的可靠性；即使标准浓度本身存在一定的误差，当基于此数据进行预测时，因为针对同一组浓度样本，且与此标准浓度进行预测对比，则实验效果的相对误差是准确的，可以进行合理有效的预测对比。选择其中的15组样本为训练集，建立SVM模型并查看模型在训练集上的回归效果；选择剩余的5组样本为测试集，用建立好的模型对测试集进行回归预测，并验证SVM模型的预测精度和水平（详情见表1）。模型的建立需要找到最优的惩罚参数c和RBF核参数g，本文采用自适应变异粒子群优化算法进行参数寻优，具体的优化流程如图3所示。

图3　自适应变异PSO参数优化流程图

优化步骤为：①选取20组实验数据中的15组做训练样本，剩余的5组做测试样本。②初始化参数c和g，建立SVM回归模型。③由于每个粒子群只能优化一个参数，因此设置粒子群的维数为2，每维粒子群中粒子的数目选取10～30为宜，本实验选择20。迭代次数为200代。根据两个参数的优化范围对粒子群的初始位置和速度进行初始化。④设置适应度函数为模型预测结果的均方差。⑤将粒子适应度值进行横向或纵向比较后获得当前群体的最优位置。根据式（1）及式（2）更新粒子的速度和位置。⑥优化流程的结束条件为模型预测结果均方差为0或者迭代次数达到设定值。未达到结束条件则转第④步。

选定好最优参数组合（c，g）后，对训练集进行训练，建立SVM回归模型，之后对测试集进行回归分析，得到测试集的模型预测结果。

所设定的优化参数为：粒子群维数为2，种群数量20，粒子群优化迭代次数200代，ω取初值为0.9，终止值为0.4，根据线性递减惯性权重LDIW（Linear Decreasing Inertia Weight）进行调整，学习因子c1=1.5，c2=1.7。由图3参数优化流程计算，可得到如图4所示的粒子群优化误差曲线。横轴为优化代数，纵轴为适应度值，即模型测试样本计算结果的均方误差。

图4　自适应变异PSO参数寻优结果图

由图4可以看出，粒子的适应度值基本在0.01～0.05之间很小的范围内，即模型预测结果的平均绝对误差很小，在4%以下，满足尾气检测标准的要求。优化200代所用时间为10.859 8 s，最优c为39.315 2，最优g为0.178 55。将得到的最优参数组合（c，g）代入支持向量机重建传感器模型，可以得到模型在训练样本和测试样本的预测结果，如图5、图6所示。其中训练样本的测试结果均方差为 5.302 63×105，测试样本预测结果的均方差为0.000 107 812。

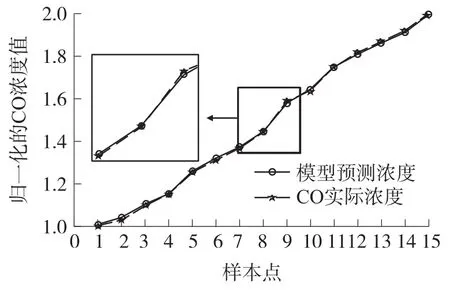
图5　CO训练集实际浓度和预测对比图

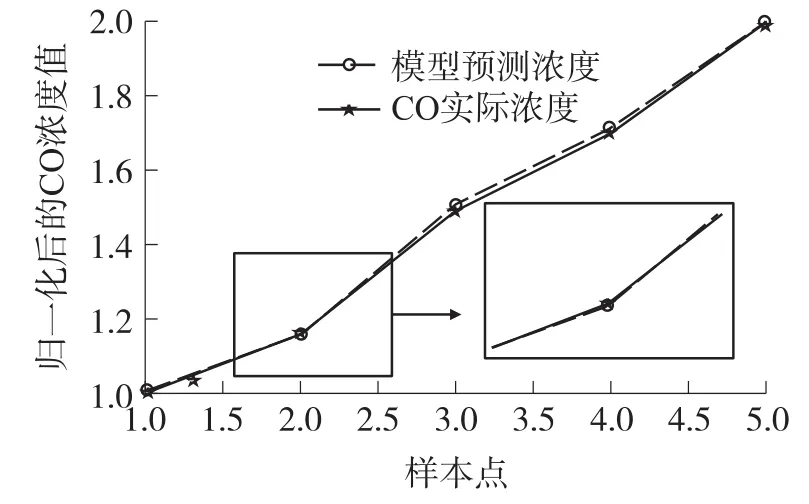
图6　CO测试集实际浓度和预测对比图

由图5可以看出利用训练集建立的模型对CO训练集本身做预测时，模型预测值和CO实际浓度值很好地吻合，误差极小；将模型应用于CO测试集的预测，如图6所示，效果明显，曲线很好地逼近真实浓度，说明本实验建立的模型预测精度高，可应用于混合气体中CO气体的回归预测。

3.2遗传算法优化BP网络建模分析

将遗传算法优化的BP网络用于同一组CO气体数据的分析中。按照如图1所示的优化流程图，具体的优化步骤为：①选取20组实验数据中的15组做训练样本，剩余的5组做测试样本，并将样本数据进行归一化处理。②确定BP神经网络的拓扑结构。本课题同时对三种组分的混合气体进行定量分析，针对不同气体采用独立建模的方法，所以设置BP神经网络的结构为4-7-1，即输入层有4个节点，隐含层有7个节点，输出层有1个节点。③初始化网络，得到网络的初始权值和阀值。④初始化遗传算法的参数。种群规模选取10～30为宜，本实验选择20；迭代次数为100代；交叉概率选在0～1之间，本文选择0.2；变异概率选择0.1。根据两个参数的优化范围对粒子群的初始位置和速度进行初始化。⑤设置适应度函数为训练数据预测误差绝对值的和。⑥初始化种群。⑦迭代寻优，求解最优的初始权值和阀值。根据式（4）～式（6）进行个体的选择、交叉和变异，将个体的适应度值进行横向或纵向比较后获得当前群体的最优个体。⑧优化流程的结束条件为模型预测误差和为0或者迭代次数达到设定值。未达到结束条件则转第⑥步。

把遗传算法得到的最优个体赋给BP神经网络，对训练集进行训练，建立神经网络回归模型，之后对测试集进行回归分析，得到测试集的模型预测结果。

根据图1优化流程计算，可得到如图7所示的遗传算法优化过程最优个体适应度值变化曲线。横轴为优化代数，纵轴为适应度值。

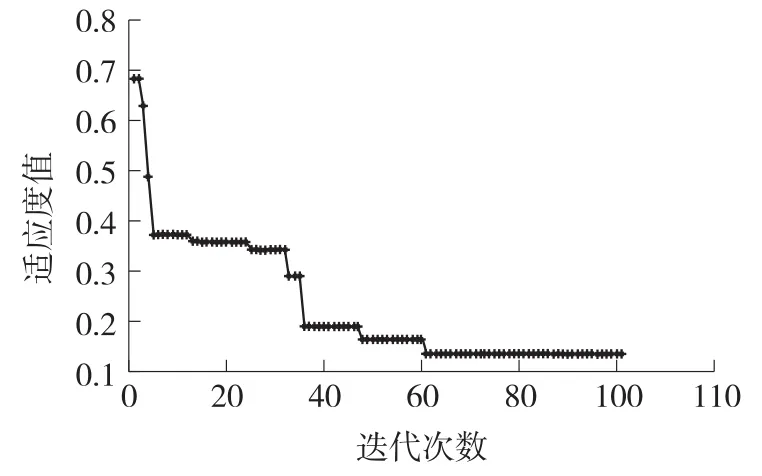
图7　最优个体适应度值变化图

由图7看出，最优个体的适应度值从最高的0.682递减至最低的0.131，大约在迭代60次之后便趋于稳定状态。将优化得到的最优个体赋给BP神经网络，用训练数据训练100次之后，可以得到模型在训练样本和测试样本的预测结果，如图8和图9所示。

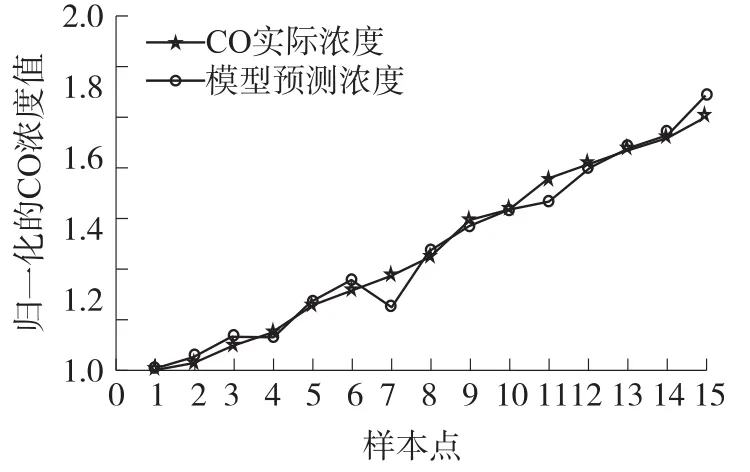
图8　CO训练集回归效果

图9　CO测试集预测效果

从图8可以看出，将建立好的回归模型查看在训练集上的回归效果，存在较大的偏差，特别在是第七个样本点处；将模型应用于测试集的分析上，由图9所示，误差十分明显，不能对测试集进行很好地回归分析。

3.3结果分析

测试数据的仿真结果及平均绝对误差如表1所示。通过实验，可以得到2种方法的优化结果对比，包括建模时间和测试结果均方差大小，如表2所示。

表1　仿真结果对比

表2　优化结果对比

由表1、表2可以看出：两种方法建立的气体定量分析模型的测试误差水平，SVM建模优于遗传算法优化BP网络。采用粒子群优化SVM，建模所需时间为87.26 s，而遗传算法优化BP网络的建模时间为2 683 s，因此SVM建模方法在处理气体定量分析问题上，不仅在建模时间上优于BP网络，而且精度水平也高于BP网络。

将支持向量机建模回归预测值与标准值之间的误差曲线，与BP神经网络模型的回归预测值与标准值之间的误差曲线作对比，如图10所示。

从图10可以清晰地看到，BP神经网络的预测误差值最大在0.05附近，且基本保持在0.02～0.05之间，波动幅度较大；SVM预测误差值围绕0上下小幅波动，误差绝对值基本维持在0～0.01之间。SVM预测水平精度明显高于BP神经网络。

图10　误差曲线对比图

4　结论

本文将自适应变异粒子群优化算法应用于支持向量机的参数寻优，对浓度范围在0.5%～8%的20组CO气体进行定量分析，选取其中15组样本作为训练集，建立了SVM回归模型，并对训练集进行预测分析，以检测模型的准确度；选择剩余的5组气体样本作为验证集，验证模型的预测精度和水平。在SVM参数的选取问题上，提出了自适应变异粒子群参数寻优法，与遗传算法优化BP网络建模相比，SVM建模时间为87.26 s，BP网络为2 683 s；SVM预测平均绝对误差为0.047，BP网络为0.08，SVM精度水平明显高于BP网络。因此，将自适应变异粒子群优化与SVM相结合更适合处理气体的定量分析，具有一定的发展潜力和可挖掘空间。

［1］ 杨永杰，张裕胜，杨赛程，等.一种PM2.5检测传感器设计［J］.传感器与微系统，2014，33（3）：76-78，81.

［2］ 余大洲.基于RBF神经网络的可燃气体检测系统的研究［D］.长安大学，2014.

［3］ 耿志广，王希武，王寅龙，等.基于人工神经网络的电子鼻对混合气体检测研究［J］.现代计算机（专业版），2010（5）：45-48.

［4］ 乔聪明.PLS-SVR的三组分混合气体定量分析［J］.太原理工大学学报，2014，45（1）：120-122，127.

［5］ 张愉，童敏明，戴桂平.基于OBLPSO-LSSVM的一氧化碳浓度检测［J］.计算机工程与应用，2013，49（24）：249-252，261.

［6］ 张其林.基于支持向量机的红外光谱混合气体组分分析［J］.计算机时代，2010，（1）：9-11.

［7］ 王智文，张记龙，王志斌，等.一种基于神经网络的混合气体体积分数预测模型［J］.传感器与微系统，2011，30（3）：67-69，72.

［8］ 曲健，陈红岩，刘文贞，等.基于改进网格搜索法的支持向量机在气体定量分析中的应用［J］.传感技术学报，2015，28（5）：774-778.

［9］ 李玉军，汤晓君，刘君华.基于粒子群优化的最小二乘支持向量机在混合气体定量分析中的应用［J］.光谱学与光谱分析，2010，30（3）：774-778.

［10］Manouchehrian Amin，Sharifzadeh Mostafa，Hamidzadeh，et al. Selection of Regression Models for Predicting Strength and Deformability Properties of Rocks Using GA［J］.International Journal of Mining Science and Technology，2013，23（4）：492-498.

［11］付华，王馨蕊，杨本臣，等.基于MPSO-CWLS-SVM的瓦斯涌出量预测［J］.传感技术学报，2014，27（11）：1568-1572.

［12］付华，王馨蕊，王志军，等.基于PCA和PSO-ELM的煤与瓦斯突出软测量研究［J］.传感技术学报，2014，27（12）：1710-1715.

［13］Andrews P S.An Investigation into Mvolutionary Operators for Particle Swarm Optimization［C］//IEEE Congress on Evolutionary Computation，Vancouver，2006：1029-1036.

［14］Parsopoulos E，Vrahatis M N.Parameter Selection and Adaption in Unified Particle Swarm Optimization.Mathmatical and Computer Modeling，2007，46（3）：198-213.

［15］马永杰，云文霞.遗传算法研究进展［J］.计算机应用研究，2012，29（4）：1201-1206，1210.

［16］袁力哲，杨宪江，王宇.基于自适应遗传BP算法的混合气体定量检测研究［J］.仪表技术与传感器，2013（6）：118-120.

郑尧军（1974-），男，浙江嵊州人，副教授，浙江省汽车检测与维修专业带头人，研究方向为车辆工程技术，zhengyaojun@ 126.com；

陈红岩（1965-），男，浙江杭州市，教授，研究生导师，浙江大学内燃机工程专业硕士、博士学位；上海交通大学动力与机械工程专业博士后。主要研究领域为汽车电子、发动机排放与控制等，bbchy@ 163.com。

Application of Support Vector Machine Optimized by Particle Swarm in Quantitative Analysis of Gas

ZHENG Yaojun1*，CHEN Hongyan2，FENG Yong1，CHEN Kaikao1，QU Jian2
（1.College of Automotive Technology，Zhejiang Technical Institute of Economics，Hangzhou 310018，China；2.College of Mechanical and Electrical Engineering，China Jiliang University，Hangzhou 310018，China）

For the problems of the quantitative analysis of vehicle exhaust emissions of CO gas，it is difficult to determine parameters of SVM modeling，calculate excessive data in infrared spectroscopy，and other issues.A solution of support vector machine of adaptive and mutate particle swarm optimization was proposed.20 different groups of CO gas which concentration range from 0.5%to 8%was analyzed.According to this method，the spectrum data of CO in vehicle exhaust is optimized.The kernel function was used in SVM to analysis the concentration.Then compare the effect with the result received with the BP neural network model.The result shows that the best parameter in PSO is c=39.315 2 and g=0.178 55，the fitness of BP neural network became stable after 60 iterations，the time of modeling by SVM was about 1/30 of BP modeling，and the prediction accuracy of SVM is significantly higher than BP.Compared with BP network，SVM is more suitable for processing quantitative analysis of gas.

sensor application；SVM；particle swarm optimization；bp neural Network；genetic algorithms

TH744

A

1004-1699（2016）07-1121-06

2015-12-13修改日期：2016-03-12