基于Markov理论的加权非等距GM(1,1)预测优化模型

李志伟，李克昭,2

(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000；2. 北斗导航应用技术协同创新中心,河南 郑州 450052)



基于Markov理论的加权非等距GM(1,1)预测优化模型

李志伟1，李克昭1,2

(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000；2. 北斗导航应用技术协同创新中心,河南 郑州 450052)

背景值的构造方法是影响加权非等距GM(1,1)预测模型的精度和适应性的关键因素。文中通过等分函数法构造新的背景值对传统的加权非等距GM(1,1)模型进行优化，优化后的模型使其同时适应于高增长指数序列和低增长指数序列，提高传统模型的预测精度和适应性能力。但是优化后的模型依然易受建模数据随机扰动影响。马尔科夫(Markov)模型具有削弱建模数据的随机扰动性的优势。基于此，将优化的加权非等距GM(1,1)模型和Markov理论有机结合，构建优化的加权非等距Markov-GM(1,1)预测模型。最后，结合秀山湖二期工程的变形实测数据，运用新陈代谢的计算模式进行预测验证。结果表明：优化的加权非等距Markov-GM(1,1)预测模型的拟合和预测精度都优于传统的加权非等距GM(1,1)预测模型，新的预测模型的适用性更强，具有实际的参考价值。

加权非等距GM(1,1)模型；背景值；等分函数法；新陈代谢；变形监测

变形监测工作可为建筑物安全运营、山体滑坡和矿区塌陷灾害的预防和治理等工作提供科学的决策依据。在原始变形监测数据的基础上，如能构建合理的预测模型，不仅为变形监测工作提供先验信息，而且还能为灾害预防提供判断依据，可把灾害的损害降低到最小。尤其在GNSS自动化监测系统中，预测方法及合理预测模型的引入，有可能实现山体滑坡、矿区塌陷等突发灾害的实时监测或及时预测。灰色系统理论是一种针对研究资料较少、实测数据贫乏以及不确定性问题的理论。变形监测数据本身具有一定的灰性，应用灰色系统理论建立预测模型是合适的。

灰色系统理论的预测模型有多种，其中用于变形监测的灰色预测模型主要有灰色GM(1,1)[1]，初值、背景值以及残差优化的灰色GM(1,1)模型[2-4]，最小二乘优化的灰色GM(1,1)模型[5]，灰线性组合模型[6-7]等。这些模型都是基于等时距的灰色预测建立的，而在变形监测的实际工作中，监测的时间序列往往是非等距的。因此，很多学者就针对非等距时间序列，构建灰色非等距GM(1,1)预测模型[8-10]，并应用到变形监测工作中，取得一定的成果。但是，传统的非等距 GM(1,1)预测模型本身固有的系统误差给预测工作造成一定的负面影响。本文通过等分函数法构造新的背景值对传统的加权非等距GM(1,1)模型进行优化，优化后的模型同时适应于高增长指数序列和低增长指数序列，提高传统模型的预测精度和适应性能力，结合 Markov理论具有削弱建模数据的随机扰动性的优势[11-13]，构建优化的加权非等距Markov-GM(1,1)预测模型。最后，结合秀山湖二期工程的变形实测数据，运用新陈代谢的计算模式对新模型进行预测验证。

1　优化的加权非等距Markov-GM(1,1)预测模型

1.1传统的加权非等距GM(1,1)模型

[8-10]，传统的加权非等距GM(1,1)模型的建模步骤如下：

(1)

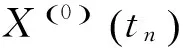
(2)

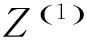
(3)

步骤4加权非等距GM(1,1)模型的白化灰色微分方程为

(4)

式中：a为发展系数;b为灰作用量。加权非等距GM(1,1)模型的差分灰色微分方程为

(5)

令参数矩阵

(6)

步骤5构造背景值矩阵B和向量Yn。

(7)

(8)

步骤7加权非等距GM(1,1)预测模型方程，即

(9)

步骤8恢复时间序列还原预测值,即

(10)

1.2等分函数法构造背景值

图1　传统背景值序列的构造示意图

图2　新背景值序列的构造示意图

(11)

因此，4个小区间面积和为

(12)

同理可得，当区间被分为n份时，n个小区间的面积和为

(13)

(14)

1.3基于Markov理论修正优化的加权非等距GM(1,1)预测模型

将上述背景值重构的加权非等距GM(1,1)模型与Markov理论有机结合，构建优化的加权非等距Markov-GM(1,1)预测模型，参考文献[11-13]，建模步骤如下。

1)划分Markov状态。计算优化的加权非等距GM(1,1)模型的预测值与残差序列，并据此划分s个Markov状态区间为

(15)

4)编制预测表。选取距离预测值目标最近s个原始对象，按照从近到远的顺序，所需的转移步数分别为1,2,…,s。在转移步数所对应的转移矩阵中，取起始状态所对应的行向量，即为各状态出现的概率，并将各自的概率求和，其最大的概率所对应的状态即为预测值所对应的状态。

2　实例计算与结果分析

该工程是对秀山湖二期工程中的7幢楼进行沉降观测(12#、13#、15#、18#、19#、20#、21#)。文中以第12#楼为例，由工作基点G3开始对12#楼的沉降点进行观测，按照二等水准测量的要求进行往返测，对变形监测点进行11期监测，观测精度均符合二等水准测量的技术要求，选取12-2、12-4和12-6号点的累计沉降数据为原始数据，如表1所示。

表1　实测沉降累计数据表

2.1优化的加权非等距Markov-GM(1,1)预测模型数据计算过程

以Matlab7.0软件为平台，为使建模数据和预测值有很好的相关性，同时能够验证预测模型的预测能力。文中取表1中前7数据建模，构建优化的加权非等距Markov-GM(1,1)预测模型，利用新陈代谢的计算模式预测第8～11期数据。以监测点12-2的第8期数据预测为例，预测模型的计算过程如下：

2)按照相对值(累计沉降量实测值与预测值的比)划分Markov状态，划分状态见表2所示。

表2　Markov状态划分标准

3)计算(一到四步)转移概率矩阵。

4)计算第8期数据所处的状态，见表3。

表3　第8期状态预测

2.2优化的加权非等距Markov-GM(1,1)预测模型结果分析

按照上述计算步骤，运用新陈代谢的计算模式，依次计算3个监测点的第8～11期的预测值。即：首先用前7期观测数据建立模型，得到第8期的预测值；然后去掉建模数据中第1期数据，加入第8期的预测值重新建模，计算第9期的预测值；依次类推，分别计算出第8～11期的预测值；最后，取最后一次新陈代谢过程中所产生的拟合值和预测值，作为优化的加权非等距Markov-GM(1,1)预测模型的拟合值和预测值。

2.2.1拟合值计算结果

传统的加权非等距GM(1,1)和优化的加权非等距Markov-GM(1,1)模型的3个监测点的拟合值结果，见表4～表6所示。

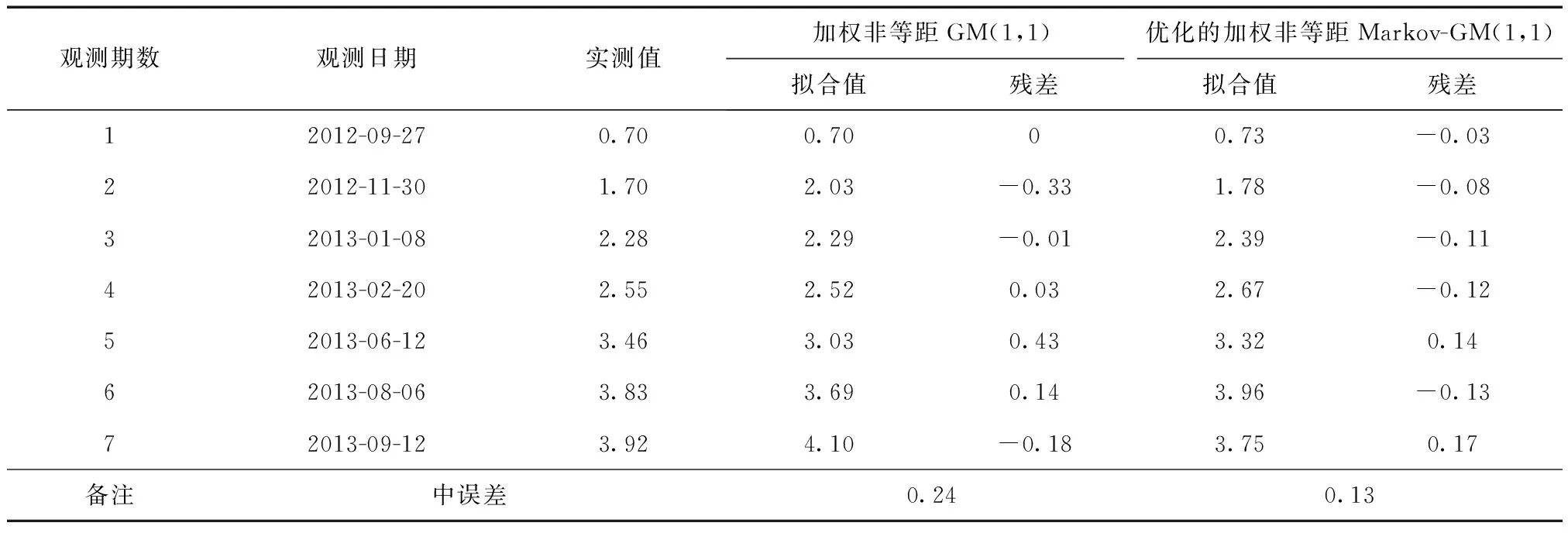
表4　监测点12-2预测模型拟合值结果　mm

表5　监测点12-4预测模型拟合值结果　mm

表6　监测点12-6预测模型拟合值结果　mm

从表4～表6中可以看出，优化的加权非等距Markov-GM(1,1)预测模型的拟合值残差中误差均小于传统的加权非等距GM(1,1)预测模型。并且三组不同的数据同时证明新模型的拟合精度优于传统的模型，验证新模型的可行性。

2)预测值计算结果。传统的加权非等距GM(1,1)和优化的加权非等距Markov-GM(1,1)模型的3个监测点的预测值结果，见表7所示。

表7　3个监测点预测值结果　mm

从表7中可以得出： 3个不同监测点的4期预测结果残差中误差显示，优化的加权非等距Markov-GM(1,1)模型的预测值残差中误差均小于传统的加权非等距GM(1,1)模型。因此，证明优化的加权非等距Markov-GM(1,1)模型的预测精度优于传统的加权非等距GM(1,1)模型。从后两期的预测值可以看出，传统模型的预测值残差相对较大，新模型的预测值更具参考价值。因此，新模型的预测精度更高，预测能力更强，模型的稳定性更强，具有实际的参考价值。

3　结束语

本文通过等分函数法构造新的背景值对传统的加权非等距GM(1,1)模型进行优化，并结合马尔科夫(Markov)模型具有削弱建模数据的随机扰动性的优势，构建优化的加权非等距Markov-GM(1,1)预测模型。同时，结合秀山湖二期工程的变形实测数据，运用新陈代谢的计算模式进行预测验证，并与传统的加权非等距GM(1,1)模型的预测结果进行比较。结果表明：优化的加权非等距Markov-GM(1,1)模型能够同时适应于高增长指数序列和低增长指数序列，提高预测模型的抗扰动能力，新模型的预测精度更高、适应能力和预测能力更强，具有实际的参考价值。

参考文献：

[1]岳仁宾,腾德贵,胡波,等.灰色模型在深基坑变形监测中的应用研究[J].测绘通报,2014(增2):85-87.

[2]袁德宝, 崔希民, 高宁.同时利用x(1)(1)和x(1)(n)为GM(1,1)建模初始条件的预测方法研究[J].大地测量与地球动力学, 2013, 33(3):79-82.

[3]郭兰兰,邹志红,安岩.基于残差修正的GM(1,1)模型在水质预测中的应用[J].数学的实践与认识,2014,44(19):176-181.

[4]谭冠军.GM(1,1)模型的背景值构造方法和应用[J].系统工程理论与实践,2000,20(4):99-103.

[5]袁豹,岳东杰,李成任.基于总体最小二乘的改进GM(1,1)模型及其在建筑物沉降预测中应用[J].测绘工程,2013,22(3):52-55.

[6]吴浩,董元锋,李奎,等.灰色系统和几何耦合的边坡变形预测模型研究与应用[J].测绘通报,2014(增2):46-49.

[7]高宁,崔希民,高彩云.高层建筑物沉降变形的灰线性预测[J].测绘科学,2012,37(3):96-98.

[8]王鸣翠,于胜文,张帅帅,等.基坑变形非等时距灰色预测模型程序设计及应用[J].测绘地理信息,2015,40(1):41-44.

[9]成枢,李强.基于非等间隔GM(1,1)模型的沉降预测[J].测绘与空间地理信息,2015,38(4):33-35.

[10] 李军亮,肖新平,廖锐全.非等间隔GM(1,1)幂模型及应用[J].系统工程理论与实践,2010,30(3):490-495.

[11] 沈哲辉,黄腾,唐佑辉.灰色-马尔科夫模型在大坝内部变形预测中的应用[J].测绘工程,2015,24(2):69-74.

[12] 王磊,武术静,李长青.灰色马尔科夫模型对煤自燃发火预测的研究[J].河南理工大学学报(自然科学版),2015,34(1):35-39.

[13] 杨锦伟,孙宝磊.基于灰色马尔科夫模型在平顶山市空气污染物浓度预测[J].数学的实践与认识,2014,44(2):64-70.

[责任编辑：张德福]

An optimized weighted non-equidistance GM(1,1) prediction model based on Markov theory

LI Zhiwei1, LI Kezhao1,2

(1.School of Surveying and Landing Information Engineering, Henan Polytechnic University, Jiaozuo 454000, China;2.Collaborative Innovation Center of BDS Research Application, Zhengzhou 450052, China)

The structure method of background value in the weighted non-equidistance GM(1,1) prediction model has an important influence on the precision and adaptability of the model. This paper optimizes the traditional weighted non-equidistance GM(1,1) model which creates a new background by divisions of function method. The optimized model is suited to build the weighted non-equidistance GM(1,1) model for both high growth index series and low growth index series. It improves the precision and adaptability of the traditional model. But the optimized model is still affected by random fluctuation of modeling data easily. Markov model has the advantage of reduce the fluctuation of forecasting the modeling data. Based on above, this paper combines the optimized weighted non-equidistance GM(1,1) model and Markov theory, producing the optimized weighted non-equidistance Markov-GM(1,1) prediction model. Finally, with data of the deformation monitoring of the second phase of Xiushan Lake project, the metabolism computing model is used to predict. The results show that the optimized weighted non-equidistance Markov-GM(1,1) prediction model of the accuracy is better than the traditional weighted non-equidistance GM(1,1) prediction model, and new prediction model performs with better applicability, which has practical reference value.

weighted non-equidistance GM(1,1); background value; divisions of function method; metabolism; deformation monitoring

10.19349/j.cnki.issn1006-7949.2016.12.008

2015-06-26

国家自然科学基金资助项目(41202245;41272373)

李志伟(1991-)，男，硕士研究生.

TU196

A

1006-7949(2016)12-0038-06