基于不同交通工具多约束条件的最短路径算法研究

范林林，李　翔，张　晶， 张江水，赵　婷

(1 信息工程大学，河南 郑州，450052；2 中国天绘卫星中心,北京 102100 )



基于不同交通工具多约束条件的最短路径算法研究

范林林1，李翔1，张晶2， 张江水1，赵婷1

(1 信息工程大学，河南 郑州，450052；2 中国天绘卫星中心,北京 102100 )

多约束条件下的最短路径选择可以满足用户的出行需求，然而不同的交通工具在相同起始点下最短路径选择存在很大差异。为了满足多用户的出行需求，基于不同交通工具的多约束条件，对传统的Dijkstra算法进行改进，由传统的基于单约束条件向多约束条件改进，并对最短路径选择的准确程度进行优化。通过实例，验证算法的可行性和准确程度。

最短路径；多约束条件；Dijkstra算法；多交通工具

最短路径问题是GIS网络分析最基本最关键的问题。所谓最短路径，不只是指地理意义上的距离最短，在交通网络分析中，最短路径可以扩展到其它的度量，如时间、费用等，相应地，最短路径问题就成为最快路径、最低费用等问题[1]。在分析运输货流的最小成本、交通网络结构、选择交通运输路线、建造和维护通讯线路、规划城市公共交通网络[2]等方面，都有着广泛的应用。

随着交通网络日益复杂，不同的用户在出行时选择的交通工具存在很大差别，在出行过程中，仅仅为用户提供路程最短路线和时间最短路线或者单一约束条件下的最短路径选择路线，已经不能满足各类用户的需求。因此，为了制定符合不同用户需求的路径方案，本文提出基于GIS对道路进行不同交通工具在多约束条件下最短路径算法，可以快速寻找最短路径，满足多用户的不同出行需求。

1　基于不同交通工具约束道路网络数据模型的建立

1.1车辆和道路属性表的设置

本文主要是针对大型卡车、中小型客车、小轿车、出租车以及自行车的最短路径选择进行研究。所以，针对不同交通工具定义属性信息字段，如表1所示。

表1　不同交通工具属性数据设置

将真实世界中的交通网抽象为网络数据模型，构成网络的最基本的元素是线性实体以及这些线性实体的交汇点。线性实体通常称为链(Link)，交汇点通常称为结点(node)。交通网中的道路被抽象为链，将道路交汇点、拐点、收费站以及标志性建筑物等抽象为结点。为了使构建的道路网络模型更加真实，在绘制道路网时，针对道路图层的每一条道路设置其属性信息字段，如表2所示。

其中，道路的路段ID是由系统自动生成的唯一标识号；道路等级是路段所属道路的等级类型，如1为高速路，2为主干道，3为次干道等。

表2　道路属性数据设置

1.2基于不同交通工具的道路网模型建立

建立带多约束条件的道路网模型是求解带多约束条件的最短路径问题的基础，它描述交通网络中点、线、面之间的拓扑关系以及道路的每条路段的约束条件[3]。首先，遍历道路图层，读取道路的属性信息，生成弧段表，每段路段的端点信息依次加入到结点表中，并检查是否重复录入，如果有重复，则删除重复端点，生成结点表，如图1所示。

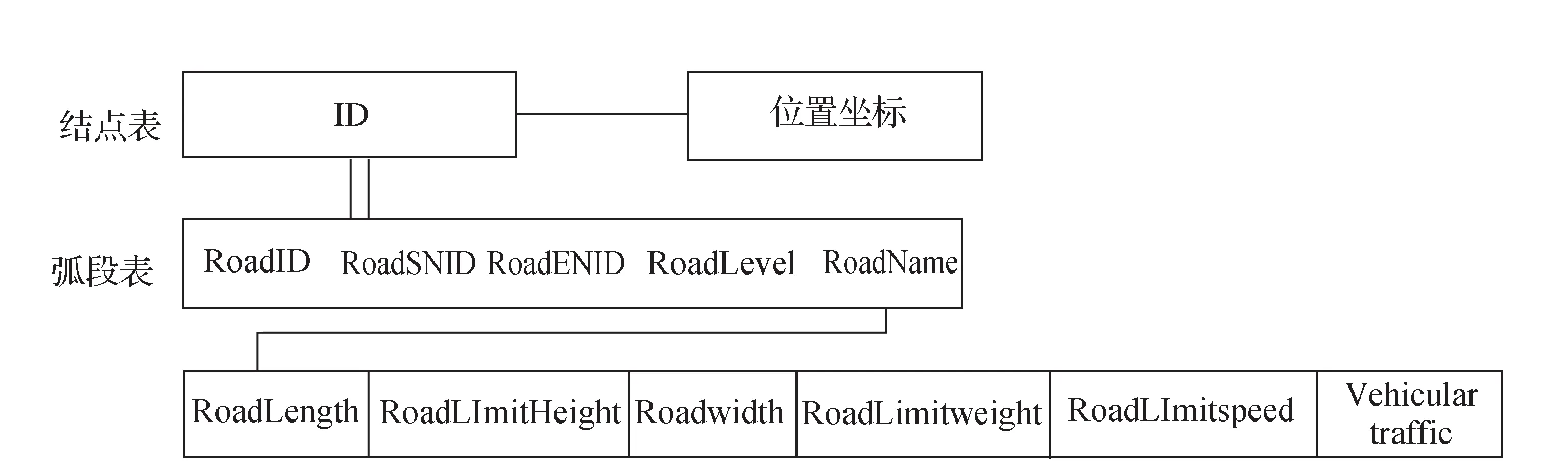
图1　结点表和弧段表

1.3基于不同交通工具的道路网模型的数据结构

本文采用前向星型结构表达道路网模型的数据结构[4]。这种数据结构表示方法是使用两个数组来表示道路网络拓扑关系，一个数组存储弧段相关数据，另一个数组存储结点相关数据。弧段的存储为一条弧段以两个结点表示。结点数组是存储结点标号，以此结点为起点的第一条弧段在弧段数组中的位置以及该结点的出度。通过结点数组，可以很容易搜索到与此结点相连的弧段的位置。图2为简化的道路模型，前向星型结构数据表示方法如表3和表4所示，表3为存储结点相关数据，表4为存储弧段相关数据。

图2　简化的道路模型

结点ID结点连接弧段结点出度111212324432541632731861

表4　弧段数组

2　基于不同交通工具的最短路径算法的研究

2.1多约束条件下的最短路径问题描述

多约束路径问题是一种在给定的带有多个约束条件的网络拓扑结构中寻找一条或多条满足限定条件的路径问题[5]。多约束最短路径问题是在多约束路径问题的基础上给这些约束制定一个综合评估函数，在满足多约束路径问题的前提下，评估函数值最小的路径就是多约束最短路径[6]。本文主要是研究不同交通工具在起点和目标点已知并确定的情况下进行多约束条件的最短路径求解问题。

给定一个有向的多个权值的道路交通网络图Q=(N，R，W)、起始结点Ns、目标结点Ne和一个约束向量C，其中N是道路结点集，R是道路路段集，W是每条路段的约束向量集，每条路段的约束向量C是非负的。设vi，vj是结点集V中两个相连的结点，道路边上有n个约束值，则有wk(vi，vj)≥0，其中k∈[1，n]，寻找从Ns到Ne的路径P，满足wk(P)≤ck，k∈[1，n]的问题就叫做多约束路径问题[7-9]。该问题存在一个或多个解P，设路径P的评价函数为

(1)

设结点状态S={node，EP，P}，其中S为从起始结点到当前结点的评价值,

(2)

式中:node是网络结构中的结点;EP是j结点状态对应路径的评价函数;P用来存储搜索路径中到达当前结点的前一个结点[11]。

2.2道路网中基于不同条件的最优路径权值设计

在越来越复杂的交通模式下，对于不同用户来说，所选择的交通工具不同，则相同起始点情况下所选择的路径存在很大的差别。现实生活中，用户的出行主要考虑的是：出发点和目标点之间基于不同交通工具是否可通行、出发点与目标点之间的距离最短、出发点与目标点之间的时间最短以及出发点与目标点之间的费用最少。

1)不同交通工具通行度：主要是道路的承重、限宽、限高以及大型车辆禁止通行路段，所以道路的权值取0或者1；其中0表示该路段不可通行，1表示该路段可以通行。

2)距离最短：当选择距离最短时，道路的权值直接取路段长度，为

(3)

式中：wij表示两个结点vi，vj之间路段的权值；dij表示两个结点vi，vj之间的距离。

3)时间最短：当选择时间最短时，会优先选择高速路以及避开拥堵路段，所以道路的权值取

(4)

式中：λ1为高速路的比例系数；λ2为路段拥挤状况比例系数。

4)费用最少：当选择费用最少时，会选择避开收费路段，考虑距离相对较短的路段以减少燃油费用，所以道路的权值取

(5)

式中：λ1为收费路段的比例系数；k是不同类型交通工具的收费标准。

2.3改进Dijkstra算法应用于多约束条件下的最短路径求解

Dijkstra算法是解决单源点单约束条件下最短路径问题最经典、比较有效的算法[12]，所以通过对Dijkstra经典算法的改进来实现多约束条件下的最短路径选择问题。

根据抽象的道路网模型，将道路的通行高度(RoadLimitHight)、通行宽度(RoadLimitWidth)、通行重量(RoadLimitWeight)、通行速度(RoadLimitspeed)以及是否允许大型交通工具通行(Prohibited Vehicles)作为约束条件加以约束。为了实现基于某种交通工具的最短路径查询，在查询前，需要设置该类交通工具的最大通行高度(MaxHight)、最大通行宽度(MaxWidth)、最大通行重量(MaxWeight)、最大通行速度(RoadLimitspeed)以及在某个路段是否允许通行(1/0)。

设置一个通行函数F(x)，当车辆满足通行高度、通行宽度、通行重量、通行速度以及允许该类车辆通行的条件时，F(x)的状态表现为“true”；当车辆对于4项指标至少有一项不满足时，F(x)的状态表现为“false”。

F(x)=(RoadLimitHight(x)>MaxHight(x)&&RoadLimitWidth(x)>MaxWidth(x)&&RoadLimitWeight(x)>MaxWeight(x)&&RoadLimitspeed(x)>Maxspeed(x)&&1)

通过判断F(x)的值，不仅限制了不同类型车辆通行，同时可以减少算法的搜索范围，提高算法的计算效率。

多约束Dijkstra算法(M-Dijkstra)流程如图3所示。

图3　多约束条件下Dijkstra算法改进流程

2.4基于不同交通工具的多约束条件下最短路径算法的实现

基于不同交通工具的最短路径选择问题应用改进Dijkstra算法求解最短路径的具体实现过程如下：

第一步：选择出行的交通车辆，根据系统设置，会自动为选择的交通车辆进行属性赋值，包含VehicleMhight(汽车通行的最大高度)、VehicleMwidth(汽车通行的最大宽度)、VehicleMweight(汽车通行的最大重量)、VehicleMspeed(汽车通行的最大速度)以及根据VehicleID(汽车标识)确定所禁止通行的道路路段。

第二步：在地图上选择StartPoint(起点)和EndPoint(目标点)两个结点。

第三步：首先判断StartPoint和EndPoint是否连通，如果连通，则进入下一步，否则，终止。

第四步：根据确定的StartPoint和EndPoint，用改进的Dijkstra算法计算基于不同的交通工具在多约束条件下的最短路径。

第五步：将计算得到的最短路径可视化显示在地图上(见图4)。根据交通工具的不同，选择不同色彩可视化每一条最短路径。

3　应用案例与分析

在实际生活中，由于用户需求的复杂性，导致用户在选择交通工具时的多样性。由于不同的交通工具在选择最短路径问题上存在着很大的差异，根据不同的需求，在选择不同交通工具的基础上，为不同的用户规划出合理的通行方案。例如，在城市交通中，居民社区、步行街道以及一些狭窄的街道等都是小型交通工具以上车辆禁止通行的；在高速路上，物资器材的运输路线要考虑收费站问题、隧道限高问题以及道路桥梁的承重问题等。所以，针对用户出行问题，为不同的用户提供合适的交通工具最短路线是一个值得研究的问题。在本文中，基于不同交通工具选择最短路径问题转化为多约束条件下的最短路径选择问题。

3.1不同交通工具的多约束条件下最短路径案例

本文实验所采用的数据是美国旧金山这一城市地区的道路网络数据。通过交通网络案例来讨论改进的Dijkstra算法在不同交通工具选择最短路径时的应用。为了更好地证明Dijkstra算法的可行性，对道路模型进行简化处理，在道路路段上设置3个约束条件，分别是：收费系数、路段长度和能否允许大型车辆通行，以实现费用最少为目标的最优路径选择。其中：① 收费系数与交通工具的类型有关，所以，当选取不同的交通工具时，道路的约束条件会发生变化，不妨设收费系数为K。② 路段长度会影响交通工具的燃油量，进而影响消耗金额，不妨设每升汽油的单价为m，m>5，则在路段上不同交通工具由路段长度影响的金额描述为M=k×m×dij。③自行车不允许在高速路上行驶。

图4　对基于不同交通工具在多约束条件下的最短路径算法的可视化表达

通过对道路添加约束条件，分别得到大型卡车(big car)、中小型客车(small car)、私家车(home car)和自行车辆(bike)的基于相同起止结点的路线选择。通过对不同交通工具在相同起止结点下的高速收费系数、全程费用、全程行驶距离以及全程行驶时间进行描述，结果如表5所示。

表5　不同交通工具的多约束条件下的路径规划结果

3.2案例算法效率分析

基于不同交通工具的多约束条件下的最短路径选择采用的算法是对经典的Dijkstra算法进行改进，由原来算法中的单个约束条件增加为改进后的多个约束条件，对改进算法后得到的结果、经典算法得到的结果以及实际结果进行对比分析，其中，根据统计不同车辆在相应路段的行驶时间得出的平均值作为该实验的实际结果与算法得到的结果进行比较。对比结果如表6所示。

经上述结果分析，本文得出如下结论：在道路连通的情况下，改进的Dijkstra算法可以基于不同的交

通工具在多约束条件下解决最短路径选择问题。通过比较实际情况的行驶时间和基于改进的算法求解出的行驶时间得到的准确度，得出改进后的Dijkstra算法具备良好的寻找最短路径的能力，改进与实际的百分比越高说明改进的算法基于不同交通工具的准确性越高，所以根据改进与实际的百分比得出改进的算法对私家车、自行车、中小型客车的适用性较强，对大型卡车的适用性相对较弱一些。通过比较改进算法得到最短路径的行驶时间和经典算法得到的最短路径的行驶时间进行对比，得出增加多个约束条件可以提高最短路径选择结果的准确性。

表6　两种算法的准确度比较

4　结束语

随着经济的快速发展，用户对于采用不同交通工具所选择的路径规划需求也在不断提升，本文的目的在于为不同需求的用户提供最合理的路线。分别获取不同交通工具的属性信息以及道路的属性信息，对道路建立道路网模型，并对经典的Dijkstra算法通过增加多个约束条件进行改进，应用改进的Dijkstra算法求解基于不同交通工具的多约束条件下的最短路径问题；最后，通过对两种算法之间以及改进算法结果与实际结果的比较，说明改进的算法不仅具有良好的寻找最短路径的能力，同时也在原来算法的基础上提高结果的准确性。本文不仅为广大不同需求的用户在使用不同交通工具选择最短路径时提供合理的路径规划，也为Dijkstra算法的应用开拓更广阔的发展空间。

[1]郭仁忠.空间分析[M].北京:高等教育出版社，2001.

[2]邬伦，刘瑜，张晶，等.地理信息系统：原理、方法和应用[M].北京:科学出版社，2002.

[3]张喜.带路径约束的最短路径问题与数据流查询技术研究[D].长沙:国防科学技术大学，2007.

[4]秦昆.GIS空间分析理论与方法[M].武汉:武汉大学出版社，2010.

[5]LI Y，HANGNS J，HOLTE R.Fast exact multi-constraint shortest path algorithms[C]. IEEE Communications Society subject matter experts for publication in the ICC 2007 Proceedings，123-130.

[6]JAFFE J M. Algorithms for finding paths with multiple constraints [J]. Networks，1984，14:95-116.

[7]邹永贵，魏来.带多约束条件的最优路径选择算法研究[J].计算机应用，2008，28(5) :1101-1103.

[8]王欢，张雁，陈旭.基于开源pgRouting的WebGIS最短路径算法实现研究[J].测绘与空间地理信息，2015,38(2)：81-84.

[9]吴超辉，滑腾飞，周永望.基于ESPO算法的装甲部队城市道路机动路径选择[J].测绘与空间地理信息，2015,38(3)：4-6.

[10] 廖建军.基于道路交通网络的多约束最优路径算法研究[D].南京:南京理工大学，2009.

[11] 王海梅.基于GIS的最优路径算法研究与实现[D].南京:南京理工大学，2008.

[12] 乐阳，龚健雅.Dijkstra最短路径算法的一种高效率实现[J].武汉测绘科技大学学报，1999，24(3) :209-212.

[责任编辑：张德福]

Research on the shortest path selection based on differenttransportation under multiple constraints

Fan Linlin1, LI Xiang1, ZHANG Jing2, ZHANG Jiangshui1, ZHAO Ting1

(1.Information Engineering University, Zhengzhou 450052, China; 2.China Tianhui Satellite Center, Beijing 102100, China)

The shortest path selection under the multiple constraints can meet user’s requirements. However, there is a big difference among different means of transportation in the same starting point for the shortest path selection. In order to satisfy the user’s travel demand, in this paper, the traditional Dijkstra algorithm is improved, which applies the shortest path query with different traffic tools under multiple constraint condition. In the process of the algorithm improved, the accuracy of the shortest path selection is optimized. An example shows the final visual result can verify the feasibility and the accuracy of this algorithm.

shortest path; multiple constraint condition; Dijkstra algorithm; multiple transportation vehicle

10.19349/j.cnki.issn1006-7949.2016.12.007

2015-07-22

国家科技支撑计划资助项目(2012BAK12B02)；国家自然科学基金青年科学基金项目(41401467)；国家自然科学基金面上项目(41471336)；国家自然科学基金资助项目(41271450)

范林林(1991—)，女，硕士研究生.

P208

A

1006-7949(2016)12-0032-06