基于抗差估计的实时单站GPS同震速度获取方法

鲁洋为，王振杰

(中国石油大学(华东) 地球科学与技术学院，山东 青岛 266580)



基于抗差估计的实时单站GPS同震速度获取方法

鲁洋为，王振杰

(中国石油大学(华东) 地球科学与技术学院，山东 青岛 266580)

基于实时单站GPS载波相位历元差分测速模型，引入抗差最小二乘估计，并根据IGGⅢ方案选择合适的等价权因子来削弱小周跳和粗差对结果的影响，并采用一组静态数据和2011年日本“3.11”地震期间MIZU站的高频数据对算法进行测试。结果表明，在含有小周跳和粗差的情况下，抗差最小二乘估计能够明显改善解算速度，可以实时获取测站毫米级的同震速度。

同震速度；实时单站GPS历元差分；抗差最小二乘估计；小周跳与粗差

采用GPS技术获取高精度的同震速度是GPS地震学的研究热点[1-5]。常用的GPS测速方法主要是基于相对定位和精密单点定位技术的位置差分法[6-7]。相对定位技术是利用差分方法获取地震台站间的基线向量来提取地表同震速度与位移[8]，该方法得到的是台站与基准站之间的相对速度与位移，因此解算结果与基准站密切相关。在地震时刻，基准站受到地震的影响是难免的，即使基准站距离震中足够远，长距离高实时相对定位中模糊度解算也是一大难题，难以达到较高的精度[9]。精密单点定位技术需要精密星历与钟差产品，不能保证实时性，而目前的实时精密单点定位技术尚未成熟[10]。由于上述方法的不足，许多学者提出采用原始多普勒观测值或载波相位变率确定测站速度[9-12]。Colosimo等提出采用载波相位历元差分结合广播星历的方法，实时估计历元间的测站位移，对位移量去噪积分，又可以得到测站总位移[3]，对于1Hz数据，历元间位移即为速度值。该方法基于单站GPS能够实现测站实时同震速度与位移的估计，但在参数估计时，采用经典最小二乘法，对小周跳和粗差的抵抗能力差。为此，刘腾等提出基于拟准检定的改进算法[4]，能够较好的定位和估计小周跳和粗差，但该算法运算复杂，计算量大。本文基于历元差分测速模型，引入抗差最小二乘估计，使用IGGⅢ方案[13-14]选择合适的等价权因子，对含有小周跳和粗差的观测值进行降权，削弱小周跳和粗差对结果的影响，并通过算例说明算法的有效性。

1　单站GPS历元差分测速模型

载波相位观测方程为

(1)

对相邻历元载波相位观测值作差分，顾及电离层的影响，采用消电离层组合，可得消电离层组合的历元差分观测方程为

(2)

对式(2)线性化后可得

(3)

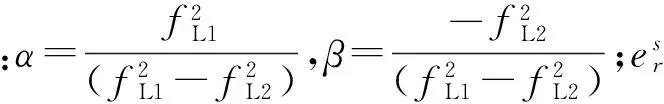
2　抗差最小二乘估计

针对单站实时GPS历元差分测速模型中的小周跳和粗差，采用抗差最小二乘估计的方法，基于权函数对异常观测值进行处理。设有下列观测方程

(4)

式中:L为观测向量，这里是历元差分观测值;A为设计矩阵;x为待估参数;Δ为观测噪声。则式(4)的抗差最小二乘解为

(5)

从式(5)可以看出，抗差最小二乘估计与传统最小二乘估计的区别在于先验权矩阵被等价权矩阵所代替，使其具有抵抗粗差的能力。在大地测量数据处理中常用的等价权函数有Huber函数、Hampel函数、Tukey函数、Andrews函数、丹麦权函数以及IGG方案权函数等。研究表明，IGG方案具有一定的优势，因此本文采用IGGⅢ方案选取等价权矩阵[13]，其等价权选择准则为

(6)

3　算例分析

3.1静态数据测速精度分析

选取一段13min的GPS静态双频数据，采样间隔为1s，对文中的算法进行测试。由于测站处于静态，故速度真值取零。首先采用经典最小二乘估计单历元解算测站速度，结果如图1所示，可以看出，测站在x,y,z 3个方向都在2cm/s以内，没有出现异常值，其RMS都在3～4mm/s，因此认为该观测数据没有小周跳和粗差。为测试算法抵抗小周跳和粗差的能力，在原始数据中L1频段上人为的添加一些小周跳和粗差，具体情况见表1。

表1　加入的周跳和粗差

分别采用经典最小二乘估计和抗差最小二乘估计单历元解算测站速度，结果分别如图2、图3所示。可以看出，加入粗差后，采用经典最小二乘估计时，x,y,z 3个方向的速度值都在加入粗差的地方出现异常值，最大异常值达到4cm/s，其RMS都明显的增大，y,z方向分别增大到10.4mm/s,12.8mm/s；当采用抗差最小二乘估计时，明显改善速度的估计效果，单历元解算没有出现异常值，估计结果的RMS值分别为4.0mm/s,4.2mm/s,4.2mm/s，与加入小周跳和粗差之前相差都在1.0mm/s左右，与经典最小二乘估计方法相比，x方向提高0.4mm/s，y,z方向精度分别提高到原来的2.5和3.1倍，这说明文中提出的算法能够很好地抵抗小周跳和粗差对测速结果的影响，如表2所示。

图1　不含周跳和粗差时LS解算结果

图2　加入小周跳和粗差时LS解算结果

图3　加入小周跳和粗差时RLS解算结果

表2　静态数据测速精度分析mm/s

3.2基于抗差最小二乘估计的GPS同震速度获取

选取2011年日本“3.11”地震期间MIZU站5:45:00～5:59:59时间间隔内，1HzGPS双频数据提取测站同震速度，与静态数据处理方式相同，人为的加入小周跳和粗差，具体情况如表3所示，由文献[5]可知，这些小周跳和粗差很难被探测出来。

表3　加入小周跳和粗差

首先采用经典最小二乘估计，对未加入小周跳和粗差前的GPS数据提取同震速度，解算结果如图4所示，可以看出，在没有小周跳和粗差的条件下，解算的测站同震速度比较平滑，与其他学者解算的结果很好的相符[1,5]。

在按表3加入小周跳和粗差后，分别采用经典最小二乘估计和抗差最小二乘估计提取测站的同震速度结果如图5、图6所示。

由图5可以看出，当加入小周跳和粗差后，若仍采用经典最小二乘估计提取地表同震速度，则会在加入小周跳和粗差的时刻出现异常值，如在x方向，在15，16，75，76，790历元处均出现跳跃，并且在15，16历元处达到15cm/s，而在未加入小周跳和粗差时，在这些历元处均未出现异常值，同时在y,z方向某些历元处也均出现异常值。当采用抗差最小二乘估计时，其估计结果如图6所示，由图可以看出，估计结果比较平滑，在图5中出现异常值的历元处并未出现异常，其结果与未加入小周跳和粗差时最小二乘估计的结果接近。

图4　未加入小周跳和粗差时LS解算结果

图5　加入小周跳和粗差时LS解算结果

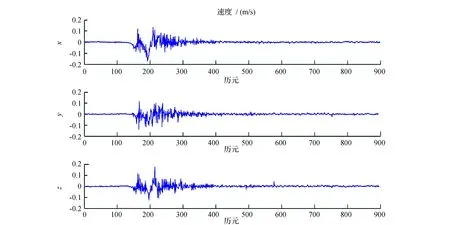
图6　加入小周跳和粗差时RLS解算结果

将未加入小周跳和粗差时经典最小二乘估计的结果与加入小周跳和粗差时抗差最小二乘估计的结果比较，统计其RMS值见表4，速度在x,y,z 3个方向的RMS分别为2.2mm/s,2.3mm/s,2.8mm/s，说明抗差最小二乘估计能够很好的抵抗小周跳和粗差，在含有小周跳和粗差的情况下，仍能够获得与“干净”数据时经典最小二乘估计估计相当精度的测站同震速度。

表4　抗差最小二乘估计RMS统计　mm/s

4　结　论

本文将抗差估计引入到历元差分测速模型中，通过IGGⅢ方案选择合适的等价权因子来削弱小周跳和粗差的影响，实时获取高精度地表同震速度。通过算例分析表明：历元差分测速模型对小周跳和粗差很敏感，当存在小周跳和粗差时，经典最小二乘获取的地表同震速度的精度明显降低，其量级由毫米级降至厘米级；抗差最小二乘估计通过降低含有小周跳和粗差观测值的权因子，有效削弱小周跳和粗差对结果的影响，达到与不含小周跳和粗差条件下精度相当的结果，实现单站实时毫米级同震速度的提取，是对常规地震观测技术的一种很好的补充。

[1]WANGRongjiang，PAROLAIS，GEM，etal．The2011Mw9.0TohokuEarthquake：ComparisonofGPSandStrong-MotionData[J]BulletinoftheSeismologicalSocietyofAmerica，2011，103(2b)：1-13．

[2]BRANZANTIM，COLOSIMOG，CRESPIM，etal．GPSnear-real-timecoseismicdisplacementsfortheGreatTohoku-OkiEarthquake[J]IEEEGeoscienceandRemoteSensingLetters,2013，10(2)：372-376．

[3]LIXingxing，GUOBofeng，LUCuixian，etal．Real-timeGNSSseismologyusingasinglereceiver[J]GeophysicalJournalInternational，2014，198(1)：72-89．

[4]COLOSIMOG，CRESPIM,MAZZONIA．Real-timeGPSseismologywithastand-alonereceiver：Apreliminaryfeasibilitydemonstration[J]．JournalOfGeophysicalResearch，2011,116(B11302)，doi:10.1029/2010JB007941

[5]刘腾，欧吉坤，袁运斌．基于拟准检定的实时单站GPS提取同震速度的改进算法研究[J].地球物理学报，2014，57(8)：2507-2517．

[6]SALAZARD，HERNANDEZ-PAJARESM，JUAN-ZORNOZAJM，etal．EVA：GPS-basedextendedvelocityandaccelerationdetermination[J]JGeod．2011，85：329-340

[7]方荣新．高采样率GPS数据非差精密处理方法及其在地震学中的应用研究[D].武汉：武汉大学，2010．

[8]何海波，杨元喜，孙中苗．几种GPS测速方法的比较分析[J]．测绘学报，2002，31( 3)：217-221．

[9]LIMin，LIWenwen，FANGRongxin，etal．Real-timehigh-precisionearthquakemonitoringusingsingle-frequencyGPSreceivers[J]．GPSSolut，10.1007/s10291-013-0362-4

[10] 张小红，郭博峰．单站GPS测速在实时地震监测中的应用[J].地球物理学报，2013，56(6)：1928-1936．

[11]ZHANGXiaohong,GUOBofeng，GUOFei，etal．InfluenceofclockjumponthevelocityandaccelerationestimationwithasingleGPSreceiverbasedoncarrier-phase-derivedDoppler[J]GPSSolut，2013，17：549-559.

[12] 肖云，夏哲仁．利用相位率和多普勒确定载体速度的比较[J]．武汉大学学报(信息科学版)，2003，28(5)：581-584．

[13] 杨元喜．参数平差模型的抗差最小二乘解[J]． 测绘通报，1994( 6)：33- 35．

[14] 杨元喜．自适应动态导航定位[M] ．北京： 测绘出版社， 2006．

[责任编辑：张德福]

Extracting real-time coseimic velocity with a stand-alone GPSreceiver based on robust estimation

LU Yangwei , WANG Zhenjie

(School of Geosciences, China University of Petroleum,Qingdao 266580,China)

Based on the model of real-time epoch-differential coseimic velocity extraction,the robust least square estimation is introduced and the IGGⅢ principle is employed to choose the equivalent weight to lower the effect of the cycle slips and gross errors.The algorithm is tested with static GPS data and the high-rate GPS data during “March 11th” earthquake in 2011 in Japan.The result shows that robust least square estimation can improve the accuracy greatly and the accuracy magnitude of coseimic velocitys can keep on mm/ s after RLS estimation .

coseimic velocity;real-time epoch-difference; robust least square estimation;cycle slips and gross errors

10.19349/j.cnki.issn1006-7949.2016.12.010

2015-07-24

国家自然科学基金资助项目(41374008)

鲁洋为(1990-)，男，硕士研究生.

P228

A

1006-7949(2016)12-0049-06