BDS/GPS组合RTK定位性能分析

满小三，孙付平，潘国富，丁　赫，刘　帅，吴　帅

(1．信息工程大学 导航与空天目标工程学院，河南 郑州 450001; 2.广州中海达卫星导航技术股份有限公司，广东 广州 511400)



BDS/GPS组合RTK定位性能分析

满小三1，孙付平1，潘国富2，丁赫1，刘帅1，吴帅1

(1．信息工程大学 导航与空天目标工程学院，河南 郑州 450001; 2.广州中海达卫星导航技术股份有限公司，广东 广州 511400)

针对单系统RTK存在可见卫星数少等问题,文中研究BDS/GPS站间单差的RTK算法模型，该模型采用二次型函数部分最小化及LAMBDA方法联合搜索模糊度。利用该模型分析BDS/GPS组合RTK的定位性能，通过短基线实测数据分析表明：站间单差RTK模型与双差模型是等价的；BDS/GPS组合系统相比于单一系统，明显提高定位的稳健性和精度，改善模糊度固定的成功率。

站间单差；BDS/GPS；RTK；二次型函数部分最小化;LAMBDA

北斗卫星导航系统(BDS)于2012年底已提供区域卫星导航定位服务，计划于2020年完成全部星座的布设，并提供全球卫星导航定位服务[1]。北斗卫星导航系统是继美国GPS，俄罗斯GLONASS系统之后第3个建成的全球卫星导航系统。相比于单一卫星导航系统，多系统组合将显著增加可视卫星数目、改善卫星空间几何结构，从而提高导航定位的可用性、连续性和精度。多系统组合导航定位将是必然的发展趋势[2]。

目前，很多文献对BDS/GPS组合系统RTK做了相关研究，但主要是基于双差模型，对单差模型的RTK相关研究比较少。文献[3]对基于GPS/BDS组合系统的短基线单频模糊度搜索进行研究，研究结果表明组合系统的模糊度搜索成功率高于单一系统。文献[4-5]对GPS/BDS组合单频RTK进行研究，表明组合单频RTK定位精度及模糊度固定成功率高于单一系统。

本文主要研究BDS/GPS站间单差的RTK算法模型。同时，对模糊度解算采用单历元搜索方式，避免繁琐的周跳探测，减少运算量。对比分析站间单差模型与双差模型的优劣及BDS/GPS组合RTK的定位性能。

1　站间单差的RTK数学模型

1.1基本观测方程

假定r表示接收机号，r=1,…,nr，nr表示跟踪BDS,GPS卫星的接收机数量。s*表示卫星号，s*=1*,…,ms*，ms*表示接收机接受的卫星数，*表示系统号(B表示BDS卫星，G表示GPS卫星);j*表示频率号，j*=1*,…,f*，f*表示*系统的频率数。则BDS，GPS的码和载波相位非差观测方程可以统一表示为

(1)

(2)

假定接收机相位硬件延迟一阶多项式可以表示为

(3)

式中：μr,f*,φ表示为未知数。对于GPS，BDS系统而言，μr,f,φ非常小。因此，可以认为接收机硬件相位延迟只与接收机频率有关，而与卫星无关。即

(4)

1.2函数模型

假设基准站与流动站共同观测到n颗GPS卫星，m颗BDS卫星。则站间单差模型为：通过基准站与移动站之间进行站间作差，即式(1)、式(2)分别在站间作差(1表示基准站，2表示移动站)，获取码伪距和载波相位观测值的单差观测方程，即单一系统的码伪距和载波相位单差方程可以表示为

(5)

(6)

对于短基线，可以基准站与流动站的大气延迟误差相等，卫星硬件相位、码延迟可以假定为常数(其随时间变化比较小)。即单差之后，大气延迟误差、卫星硬件相位、码延迟、多路径效率被消除。

对式(5)、式(6)线性化(忽略上下标注)，可以表示为

(7)

(8)

其中，A为2n+2m×3设计矩阵，e为n+m×1维元素都为1的矩阵。

未知参数：

接收机相对三维位置：

单差接收机钟差:

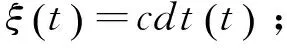
单差模糊度:

单差接收机硬件码延迟:

单差接收机硬件相位延迟:

对式(7)、式(8)中的未知参数作一定的组合，即对GPSf1硬件码延迟与接收机钟差组合；接收机硬件相位延迟与单差模糊度组合，则单差模糊度变为实数。即式(7)、式(8)可以表示为

(9)

(10)

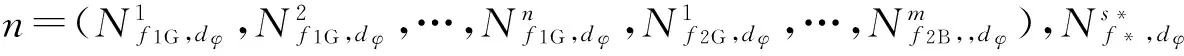
则式(9)、式(10)采用矩阵形式统一表示为

(11)

其中：

2　单差RTK 模糊度的固定

2.1模糊度固定

对于式(11)，单差模糊度为实数，因此不能直接采用LAMBDA方法搜索模糊度，需要在利用LAMBDA方法之前对单差模糊度做一定的处理。

由于式(4)可知，式(11)中的相同频率的单差模糊度具有相等的小数部分。因此可以对每个频率选取一个参考单差模糊度，通过组差方式获取整周模糊度(即为双差模糊度)。

(12)

对式(12)利用二次型函数部分最小化，可以得出式(13)。

二次型函数部分最小化[6]，主要分为两步：

第一步：

(13)

n为单差模糊度(实数)，表示为

则式(13)可以重新表示为

(14)

第二步：

(15)

利用二次型函数部分最小化可得

(16)

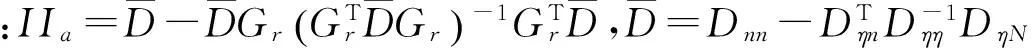
式(16)可以重新表示为

(17)

2.2模糊度固定成功率

整周模糊度解算是否正确直接影响RTK定位的精度。而模糊度固定的性能可以通过模糊度固定率来体现，即模糊度固定率可以表示为[8]

(18)

式中：NCF表示固定的历元个数；NT表示解算的整个历元总数。因此，模糊度固定失败率为：PfE=1-PSE。

整周模糊度即使固定，也不一定固定正确，为更好的反映整周模糊度固定正确与否，可以通过模糊度固定成功率体现，模糊度固定成功率表示为

(19)

式中：NSF表示正确固定的历元个数；NCF表示固定的历元个数。

3　算例分析

采用GPS/BDS双系统双频兼容型中海达接收机，在广州番禺区实测一组长度为8 km的短基线，两个站点的坐标精确已知。采样间隔为1 s，截止高度角为15°。对同类观测值之间，采用卫星高度定权方法对观测值进行定权，不同类观测值之间，采用经验值定权。例如，载波相位观测值与码观测值的权比为100∶1。首先，分别从定位精度及模糊度固定成功率方面，对比分析单差模型与双差模型的RTK,如表1～表4所示；其次，分析基于单差模型BDS/GPS RTK的定位性能，采用以下3种方案进行对比分析：①GPS;②BDS;③BDS/GPS,如图1～图6所示。

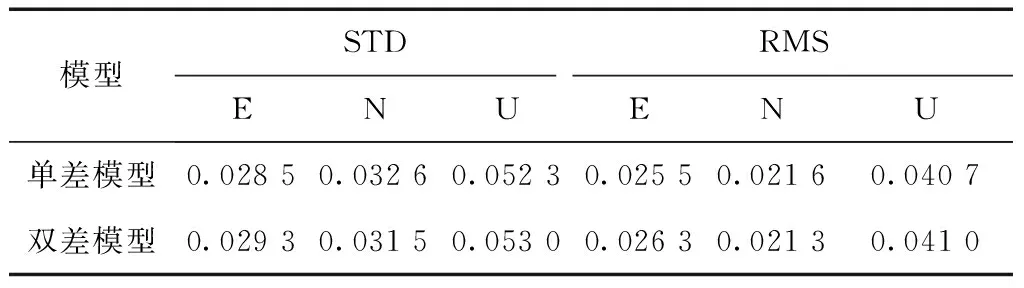
表1　单差模型与双差模型RTK在E、N和U方向的STD、RMS值

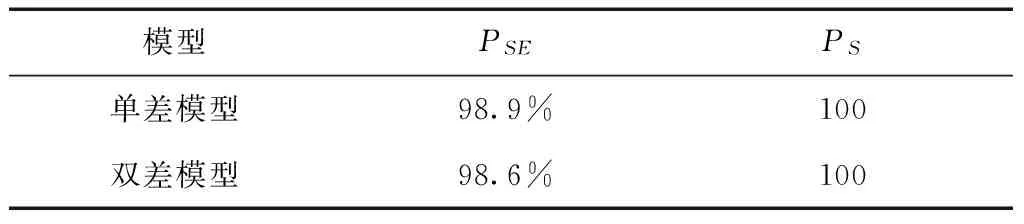
表2　单差模型与双差模型RTK的模糊度固定率及模糊度固定成功率

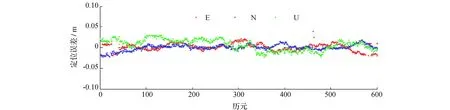
图1　基于双差模型的BDS/GPS RTK的定位误差

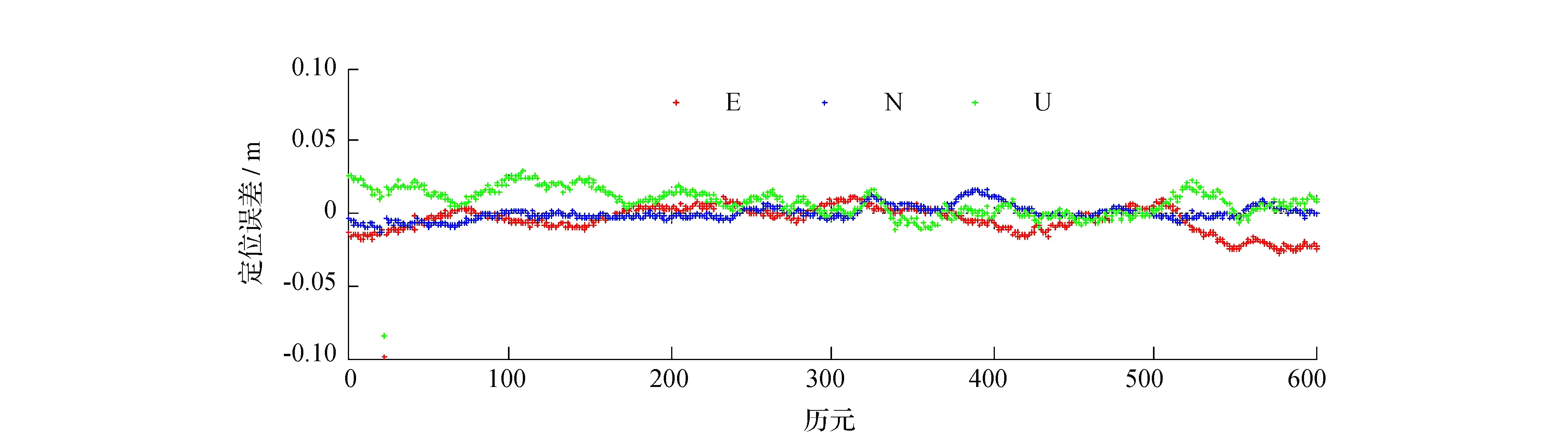
图2　基于单差模型的BDS/GPS RTK的定位误差

通过图1～图2可以看出，不论是双差模型还是单差模型BDS/GPS RTK 3个方向的定位误差都在厘米级。从表1可以看出，单差模型的BDS/GPS RTK定位精度与双差模糊的定位精度相当，单差模型(双差模型)BDS/GPS RTK在E，N和U方向的定位误差分别为2.55 cm(2.33 cm)，2.16 cm(2.35 cm)和4.07 cm(4.50 cm)。从表2可以看出，单差模型BDS/GPS RTK的模糊度固定率及模糊度固定成功率与双差模型相当。单差模型(双差模型) BDS/GPS RTK的模糊度固定率及模糊度固定成功率为98.9%(98.6%)、100%(100%)。可以看出：单差模型RTK与双差模型的RTK是等价的。

通过图3可以看出，BDS/GPS组合系统的可见卫星数明显多于BDS或GPS单一系统，为在城市、峡谷等观测环境比较差的环境中，保证定位解算所需的卫星数，提供连续定位的可能。BDS/GPS组合系统的PDOP值明显低于BDS或GPS单一系统，在整个观测期间，BDS/GPS组合系统的PDOP值低于2。

图3　3种方案的可见卫星数及PDOP值

方案STDENURMSENUBDS0.03540.04040.04760.03440.03270.0452GPS0.03130.03580.04490.02850.02320.0436BDS+GPS0.02850.03260.04230.02550.02160.0407

通过图4～图6可以看出，BDS/GPS组合系统及单系统BDS，GPS，RTK 3个方向的定位精度都在厘米级。但是BDS/GPS 组合系统RTK定位精度优于单系统BDS，GPS。BDS RTK定位精度稍微低于GPS。通过表3可以看出，BDS/GPS组合系统RTK在E，N和U方向的定位精度分别为2.55 cm、2.16 cm和4.07 cm，其定位精度优于单系统BDS(3.44 cm、3.27 cm和4.52 cm)、GPS(2.85 cm、2.32 cm和4.36 cm)。BDS RTK定位精度稍微低于GPS。表4可以看出，BDS/GPS组合系统的模糊度固定率(98.9%)优于单系统BDS(96.8%)、GPS(98.1%)；模糊度固定成功率相当。

表4　3种方案的模糊度固定率及模糊度固定成功率

图4　BDS RTK在E，N和U方向的定位误差

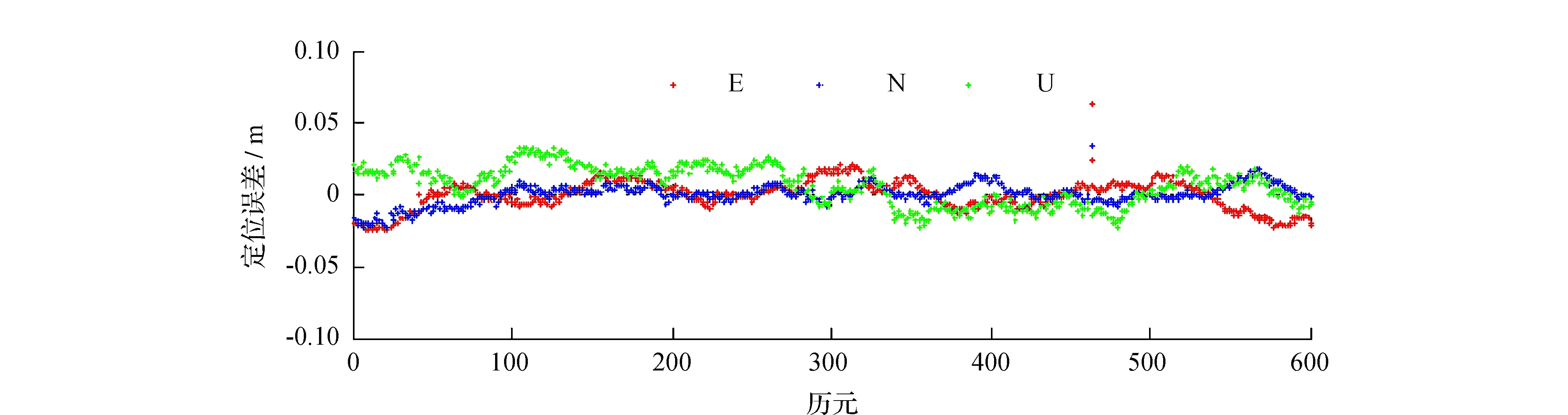
图5　GPS RTK在E，N和U方向的定位误差

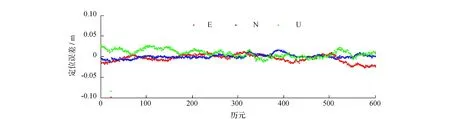
图6　BDS+GPS RTK在E，N和U方向的定位误差

4　结　论

本文研究站间单差的RTK算法模型，基于该算法模型分析短基线BDS/GPS组合系统RTK定位的性能，得出以下结论：1)站间单差模型的RTK与双差模型是等价的；2)BDS/GPS组合RTK定位精度优于单系统BDS，GPS，且其模糊度固定率优于单系统；3)GPS RTK的定位精度及模糊度固定率稍微优于BDS。

[1]宁津生，姚宜斌，张小红.全球导航卫星系统发展综述[J].导航定位学报，2013,1(1)：3-8.

[2]MAN X, SUN F.Analysis of positioning performance on combined BDS/GPS/GLONASS[C].China Satellite Navigation Conference(CSNC),2015.

[3]ODOLINSKI R,TEUNISSEN P J G.First combined COMPASS/BeiDou-2 and GPS positioning results in Australia Part I:Single-receiver and relative code-only positioning[J].Journal of Spatial Science,2013.

[4]ODOLINSKI R,TEUNISSEN P J G.First combined COMPASS/BeiDou-2 and GPS positioning results in Australia Part II:Single-receiver and relative code-only positioning[J].Journal of Spatial Science,2013.

[5]ODOLINSKI R,TEUNISSEN P J G.Quality analysis of a combined COMPASS/BeiDou-2 and GPS RTK positioning model [J].Global Navigation Satellite Systems Society IGNSS Symn,2013.

[6]LEICK A,RAPOPORT L,TATARNIKOV D.GPS Satellite Surveying[M].WILEY,2014.

[7]EUNISSEN P J L.The least squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation.Journal of Geodesy,1995,70:1-2,65-82.

[8]ODOLINSKI R,TEUNISSEN P J G.An analysis of combined COMPASS/BeiDou-2 and GPS single-and multiple-frequency RTK positioning[J].Proceeding of The Institute of Navigation PNT,2013.

[责任编辑：张德福]

Analysis of positioning performance on RTK combined with BDS/GPS MAN

Xiaosan1,SUN Fuping1,PAN Guofu2,DING He1,LIU Shuai1,WU Shuai1

(1.Information Engineering University, Zhengzhou 450001, China;2.Hi-Target Surveying Insitrument Co.,Ltd,Guangzhou 511400,China)

As to single-system RTK, the number of visible satellites is small. This paper studies the across-receiver of RTK algorithm model, which uses combined partial minimization of quadratic functions with LAMBDA method to search ambiguity. The model analyzes the positioning performance of RTK combined with BDS/GPS. The short baseline measurement data analysis shows that: the cross-receiver of RTK model is equivalent to double-difference model. Compared to a single system, the combined BDS/GPS system can significantly improve the positioning accuracy and robustness, and improve the success rate of ambiguity fixing.

across-receiver;BDS/GPS;RTK;partial minimization of quadratic function;LAMBDA

10.19349/j.cnki.issn1006-7949.2016.12.004

2015-07-09

满小三(1989-)，男，硕士研究生.

P228

A

1006-7949(2016)12-0016-05