钻孔DMI应变计法测定非均布点焊径向残余应力
陈忠安,高宗山,赵玉津,金学松
(1.江苏大学 土木工程与力学学院,江苏 镇江 212013;2.美国南卡罗莱娜大学 机械工程系,南卡罗莱纳州 803843864 ;3.天津大学 材料学院,天津 300072;4.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
钻孔DMI应变计法测定非均布点焊径向残余应力
陈忠安1,高宗山1,赵玉津2, 3,金学松4
(1.江苏大学 土木工程与力学学院,江苏 镇江 212013;2.美国南卡罗莱娜大学 机械工程系,南卡罗莱纳州 803843864 ;3.天津大学 材料学院,天津 300072;4.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
基于传统电阻应变计钻孔法无法测定点焊残余应力,提出以对中逐层钻孔的钻孔DMI应变计法来测定沿板厚方向非均匀的点焊径向残余应力。推导出了逐层钻孔所释放的径向残余应力与释放应变的关系方程;并在二维轴对称有限元模型上,采用分层加载的方法实现各层释放系数的仿真计算,标定了一个用于5层非均匀应力计算所需的释放系数表;利用该系数表,结合5步逐层钻孔测定点焊残余应力的示例,验证了该方法的有效性。
点焊径向残余应力;钻孔;DMI应变计;释放系数
电阻点焊作为一种产效率高、焊接质量好的焊接方法,被广泛用于汽车工业中[1]。焊点中一般都存在着应力集中现象,该现象的存在会造成点焊件产生脆性破坏及疲劳强度降低等问题[2-3],所以此残余应力的确定对点焊件的安全性能评估具有重要意义。
传统电阻应变计钻孔法能够较好地满足工程中一般残余应力的测定要求,但它却不适用于点焊残余应力的测定。因为点焊残余应力场是一种沿径向急剧变化的应力场,而传统电阻应变计钻孔法中的释放系数是在均匀应力场情况下推导出来的,当这种情形下得到的释放系数用于急剧变化的应力场时,将会导致测量误差出现[4-5],故此法不适用于这种径向大应力梯度场的情形。
本文提出一种将DMI应变计(DirectMeasurements,INC)与钻孔法相结合的测定新方法来测定沿板厚方向非均布的点焊径向残余应力。首先,推导获得了沿板厚方向非均布情况下的逐层钻孔释放径向残余应力与释放应变的关系方程;接着采用有限元分层加载的方法获得了应变释放系数矩阵;最后,通过测定5层非均匀点焊残余应力的示例验证了该方法的有效性。
1 非均布点焊径向残余应力的测定
1.1DMI应变计的测量原理
DMI应变计由美国直接测量公司研发,该应变计上黑色圆环区域的内、外两圆形边界为测量点所在圆边界,在同一圆边界上均布着36个测量节点,如图1所示。

图1 DMI应变计测量点分布简示图
DMI应变计上每个测点所测得的周向应变数值定义为此点半径对应的10°圆弧因变形所产生的平均应变,周向应变数值计算示意图如图2所示,O点表示应变计中心,Δθ为微段圆弧对应的夹角,r和r*分别为应变计变形前后的测点所在圆的半径,则该半径处测点的周向应变计算公式为
(1)

图2 圆弧段周向应变计算原理图
1.2沿板厚非均布点焊径向残余应力测定
点焊板件上的残余应力主要集中分布在焊点处,其是一种存在于局部且呈轴对称分布的残余应力。在离焊点较远处位置的残余应力几乎为零,即应力随着距焊点的距离增大而迅速趋近于零。经计算发现,当焊件板最小边距≥10倍的焊点半径rw时(此处定义焊点中心到焊件板边的距离为焊件板边距,下同),对应该最小边距情况下的焊件板外边界处残余应力可看作为零。为此,以10rw为半径,焊点中心为圆心,作一个大圆以建立一个轴对称的点焊简化模型,该模型如图3所示。

图3 轴对称的点焊简化模型
在该板焊点处对中钻通孔后(钻孔半径rd<焊点半径rw,该孔边不存在切向力),假设焊点中残余应力沿板厚方向是均布的,此时被释放的径向残余应力以径向压力p的形式作用在孔壁上。根据弹性力学中平面应力问题的相关理论解可知,在以焊点中心为坐标原点的极坐标系下,坐标为(r,θ)处的应力分量为[6]
(2)
将上述应力分量代入胡克定律,并像传统钻孔电阻应变计法那样,引入释放系数以简化关系式,经简化后可得盲孔情况下,钻孔释放的均布残余应力p与释放应变εθ的关系方程为
(3)
其中,E为材料弹性模量;v为泊松比;K为释放系数。

图4 点焊残余应力测量原理
残余应力沿板厚方向非均布时,可采用逐层钻孔的方法进行径向残余应力测定[7]。用DMI应变计测量点焊残余应力的原理图如图4所示,图中DMI应变计与焊点对中粘贴,然后在焊点处采用对中逐层钻孔,以释放每一层上的残余应力。此时,根据叠加原理[8],在完成第i步逐层钻孔后,通过粘贴于点焊件表面的DMI应变计测得的总释放应变为
(4)
其中,pj为第j层的平均径向应力;Kij为标定释放系数矩阵,表示当钻孔达到i步孔深时,因受到第j层的单位应力影响所引起的测量点处的周向释放应变。图5展示了一个采用3步逐层钻孔的示例。

图5 3步逐层钻孔残余应力释放系数标定图
通过预先标定释放系数表,然后在完成第i步逐层钻孔后,该层的平均径向应力计算公式可由所测应变和释放系数所表示
(5)
1.3释放系数矩阵的数据处理
对于不同的钻孔步数i,对应的释放系数Kij也是不同的。由于实验方法无法实现分层加载,故本文考虑用有限元模拟的办法对模型分层加载,以标定对应不同层深情况下的释放系数Kij。在完成第i步钻孔后,在第j层上施加径向应力场,此时测得焊点边界处的释放应变(εθ)ij,变换式(4),可得释放系数的标定公式为
(6)
这样,如果某一孔径下第i步钻孔后,通过在第j层上单独施加已知的径向应力,由于E和v是材料的常数,而焊点边界处的释放应变又可由有限元计算得到,故可通过式(6)逐个计算出方阵Kij中的每一个释放系数。
2 释放系数矩阵的有限元标定
通常,焊点直径Dw与焊件板厚度H的比值都分布在3~5之间[9],并且它们的比值大致呈线性关系[10],为体现一般性,本文选取其中间值,即比值Dw/H=4的情况进行建模分析。
考虑到连接板(即下板)的厚度对释放系数的影响无法消除,故取焊件板和连接板的厚度都为H=1;经计算发现,只要连接板的最小边距>rw,则该边距大小的变化将对系数的影响可忽略不计,为方便建模,取连接板的边距等于焊件板的边距,都为10rw;标定时所选取的应变测点位置为DMI应变计内圈测点位置。标定模型采用线弹性各向同性材料,由于释放系数是与材料属性无关的常数,所以此处取弹性模量E=210GPa,泊松比v=0.3。
用Abaqus软件按照上述参数建立二维轴对称有限元标定模型,仿真计算出5步逐层钻孔所需的释放系数表,具体网格划分如图6所示。整体模型采用8节点双二次轴对称。

图6 对中钻孔二维有限元网格划分

孔深h/H逐层钻孔对应层深度上施加单位力0.20.40.60.810.20.0989730.40.136280.0927670.60.1588480.1175330.0710210.80.1705090.128910.0858610.04497610.1752660.1335150.0909010.0527470.022141
四边形单元即CAX8单元。同时,采用结构化网格划分技术和最小化网格过渡算法,以提高应变结果的计算精度。
本文分析时,钻孔半径取0.625 rw,每层的厚度Δh=0.2H,逐层总步数为5步,标定载荷pj=1MPa。通过分层加载的方法,分析计算出五步逐层钻孔释放系数表如表1所示。
3 示例及验证
以弹性模量为70GPa,泊松比为0.33的铝合金等厚双板点焊件为例。其中,焊件板与连接板的厚度H=1mm;焊件板为半径是40mm的圆形板,连接板为半径是10mm的圆形板;焊点直径为Dw=4mm。焊点内部存在沿板厚方向变化的已知残余应力状态
σr=50(3-(1-h)2+2/r)
(7)
式中,0.5rw< r < rw;h表示深度;r为到焊点中心的距离。
要求测定距焊点中心1.25mm处焊点内部的径向残余应力。
(1)钻孔及应变测量。由于焊点半径为2mm,故选取内圈测量点半径为2.19mm的DMI应变计与焊点对粘贴于点焊件表面;选取钻头半径1.25mm的钻头进行对中逐层钻孔,每步钻孔深度为0.2H,总孔深为H。记录每步逐层钻孔后由DMI应变计内圈测点所测得的应变,记录如表2所示;

表2 DMI应变计内圈测点应变测量结果
(2)计算结果与分析。通过本文已计算好的释放系数表和所测得的释放应变,可由式(5)计算出距焊点中心1.25mm处的沿板厚非均布的径向残余应力,并将计算值与实际径向应力大小进行比较,如表3所示。其中,实际径向应力通过已知的径向应力表达式积分可得。从表中可以看出计算径向应力值与实际径向应力值非常接近,相对误差约在3%,符合工程运用中允许的误差范围。
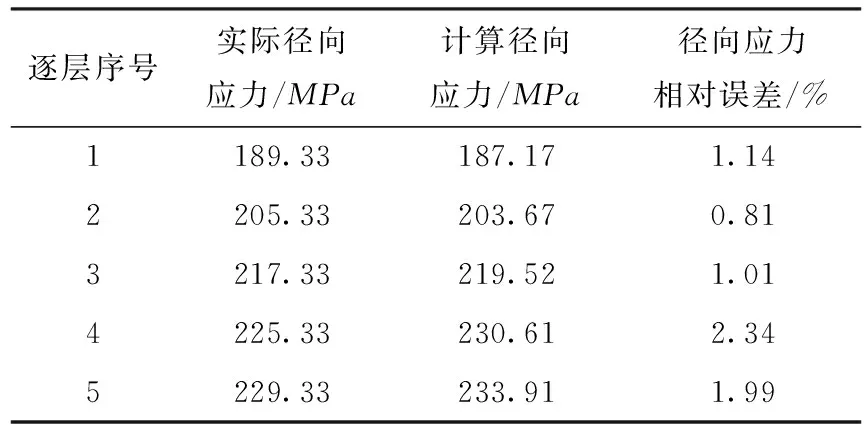
表3 逐层实际应力值与计算应力值比较
4 结束语
本文将DMI应变计与钻孔法结合,提出了一种简便易行的点焊残余应力测定新方法。在五步逐层钻孔,使用DMI应变计测定点焊径向残余应力的示例中,计算所得值与实际值比较接近,说明了钻孔DMI应变计法的有效性。
[1]JanotaM,NeumannH.Shareofspotweldingandotherjoiningmethodsinautomotiveproduction[J].WeldingintheWozrld, 2008, 52(3-4): 12-16.
[2]ChangB,ShiY,DongS.Comparativestudiesonstressesinweld-bonded,spot-weldedandadhesive-bondedjoints[J].JournalofMaterialsProcessingTechnology, 1999, 87(1-3): 230-236.
[3]ParmarRS.Weldingprocessesandtechnology[M].NewDelhi:KhannaPublishers,1999.
[4]彭守刚, 李昊. 钻孔法中释放系数导致误差的研究 [D]. 合肥: 合肥工业大学, 2012.
[5]SanjeevKKhanna,CanlongHe,HariNAgrawal.Residualstressmeasurementinspotweldsandtheeffectoffatigueloadingonredistributionofstressesusinghighsensitivitymoire′interferometry[J].TransactionsoftheASME, 2001, 123(1):132-138.
[6]LurieAI.Theoryofelasticity[M].Berlin:SpringerBerlinHeidelberg, 2005.
[7]SchajerGS.Hole-drillingresidualstressprofilingwithautomatedsmoothing[J].JournalofEngineeringMaterialsandTechnology, 2007, 129(3): 440-445.
[8]SchajerGS.Applicationoffiniteelementcalculationstoresidualstressmeasurements[J].AsmeJournalofEngineeringMaterialsandTechology, 1981, 103(2): 157-163.
[9]中华人民共和国航空工业部.HB/5276-1984 铝合金电阻点缝焊质量检验 [S]. 北京:中华人民共和国航空工业部, 1984.
[10]张文扬,郭绍庆,梁海,等.关于点焊板厚与熔核最小直径及最小抗剪强度的关系的讨论 [C].镇江: 第十六次全国焊接学术会议, 2011.
Measurement of Radial Residual Stresses in Spot Welds by the Hole-drilling DMI Strain Gage Method
CHENZhongan1,GAOZongshan1,ZHAOYujin2,3,JINXuesong4
(1.FacultyofCivilEngineeringandMechanics,JiangsuUniversity,Zhenjiang212013,China;2.DepartmentofMechanicalEngineering,UniversityofSouthCarolina, 80343864,USA;3.CollegeofMaterialScience,TianjinUniversity,Tianjin300072,China;4.TractionPowerStateKeyLaboratory,SouthwestJiaotongUniversity,Chengdu610031,China)
Residualstressofspotweldingcannotbemeasuredbytheholedrillingmethodbasedontraditionalresistancestraingauge.ADMIgaugemethodthroughcenteredlayer-by-layerdrillingisputforwardtomeasuretheradialinhomogeneousresidualstressofspotweldingalongwiththedirectionofthethicknessofplate.Therelationshipbetweenradialresidualstressandstrainthatreleasedfromtheincrementaldrillingholeisdeduced,afterwhichthehierarchicalloadmethodisadoptedtoconductthesimulatingcalculationofthereleasecoefficientsofeachlayerontwo-dimensionfiniteelementmodelandareleasecoefficientchartrequiredby5layerunequalstressescalculationisdemarcated.Theeffectivenessofthemethodisverifiedbyusingthereleasecoefficientsaswellastheexampleof5-steplayer-by-layerdrillingmethodofmeasuringtheresidualstressofspotwelding.
radialresidualstressinspotwelds;holedrilling;DMIstraingage;releasecoefficient
2015- 12- 27
国家自然科学基金资助项目(51275338);西南交通大学牵引动力国家重点实验室开放课题基金资助项目(TPL1301)
陈忠安(1955-),男,教授。研究方向:断裂力学,工程结构的疲劳与可靠性。
10.16180/j.cnki.issn1007-7820.2016.09.006
TB121
A
1007-7820(2016)09-018-04

