基于小波变换的场道脱空BP神经网络预测法研究

刘国光， 武志玮， 刘智勇， 程国勇

(1 中国民航大学 机场学院，天津　300300； 2 深圳机场，深圳　518128)



基于小波变换的场道脱空BP神经网络预测法研究

刘国光1， 武志玮1， 刘智勇2， 程国勇1

(1 中国民航大学 机场学院，天津300300； 2 深圳机场，深圳518128)

场道脱空是影响机场运行安全的重要因素之一，为研究场道脱空的无损测试，提出了基于小波变换的场道脱空BP神经网络预测法。通过室内模型试验，对缩尺模拟场道施加冲击荷载并利用小波变换法对采集到的道面竖向加速度时程信号进行功率谱分析、能量谱分析及时间-尺度分析，提取了1 500组表征场道不同脱空状况的特征向量用于进行BP神经网络训练和提升预测功能，并在某机场进行了实地测试和现场取芯以验证分析方法的可靠性;结果表明，道面振动信号经小波变换处理后反映了脱空对能量信号传递的耗散作用，在脱空和半脱空区域出现了较明显的结果差异且具有一定规律性。通过室内试验训练的BP神经网络较好地预测了现场试验结果，并能识别轻微脱空引起的信号差异，验证了该方法在评价场道脱空方面的可行性和可靠性。

道路工程；场道脱空；小波变换；BP神经网络

随着航空运输量的日益增长，脱空成为场道常见的病害。由于场道脱空在早期不能及时被发现，在飞机动荷载的反复作用及环境因素的影响下容易扩大场道脱空的程度，最终导致混凝土板的断裂，影响机场跑道正常安全的使用。因此，应该经常性检测在役场道以及时发现场道的脱空及范围，为采取有效措施修复场道的脱空提供依据。

小波变换是一种分析振动信号的有效方法，最先由法国工程师MORLET在1904年提出，是一种时间-尺度(频率)分析方法，可对信号进行多尺度细化分析。HUANG等[1]利用该方法分析地基板在移动荷载作用下动态响应，讨论了地基刚度和移动荷载速度和频率间的关系。李洪泉等[2]利用多分辨率特点将结构振动信号置于不同频段进行时频分析，用于结构损伤进行在线检测及确定损伤位置。陈仕龙等[3]利用高频段小波能量与低频段小波能量的差异，对故障电压信号进行多尺度小波变换以反映过渡电阻变化。章浙涛等[4]提出了一种基于频率顺序并依据信息类型分段的多阈值准则小波包去噪法来高效剔除各频段噪声。叶玮琳等[5]利用多阈值小波去噪算法提高具有类似机理的红外气体检测系统性能。孙磊等[6]利用重构信号的ARIMA(Autoregressive Integrated Moving Average Model)模型分析了四跨连续桥实测挠度数据，并建立了挠度预测模型。李保琦[7]通过基于小波变换与随机分析的径流模型得到了更好的复杂水文条件下径流预测值。卢正等[8]用傅里叶变换推导了附加车辆荷载与路面动力响应的解析解，研究了场道动力响应变化规律。从已有研究成果来看，小波变换方法已经得到了较广泛的工程应用，但主要集中在信号处理、模型建立和理论分析等定性分析领域，受分析技术手段限制，对经小波变换处理后信号进行定量判断的研究报道相对较少。

BP(Back Propagation)神经网络是1986年由RUMELHART和MCCELLAND提出的预测工具，已成功应用到水资源问题研究领域[9]，如水库运行[10]和降雨径流模型[11]等。崔东文[12]通过构建多隐层BP神经网络径流预测模型研究了多隐层BP网络模型，预测精度高，算法稳定。杨发群等[13]通过遗传算法(GA)对BP神经网络的初始权值和阈值进行优化提高了预测的精度。于伟等[14]结合局部均值分解LMD算法和BP神经网络算法，以实际监测位移值作为训练样本，提出了BP神经网络位移时序预测模型预测边坡体位移。彭永恒等[15]利用集成神经网络对刚性路面声响应信号进行分类识别，提取声响应信号的频域特征识别道面脱空状况。刘海平等[16]提出了基于自由响应信号与BP神经网络的结构损伤程度识别方法。通过已有研究成果可知，BP神经网络具有工程适应性、可量化性及可预测性等特点，从而为联合应用小波变换和BP神经网络分析更复杂的工程技术问题提供了技术思路。

针对场道脱空识别技术问题展开研究，以落锤激励砂土垫层道面板室内试验模型为基础，利用小波变换方法分解道面竖向加速度时程信号并进行功率谱分析、能量谱分析和时间-尺度分析，研究场道脱空状况对振动能量传递及耗散的局部时频特征，并从中提取大量表征脱空状况的特征值向量及对比向量，用于BP神经网络模型的训练与预测分析。并在某机场场道评估中进行工程应用，结合重锤式弯沉仪施加多级激励荷载，提取竖向加速度时程信号，通过小波变换和BP神经网络进行道面脱空预测，并在预测位置进行现场取芯加以验证，取得了较好的应用效果，验证了方法的可行性。

1　基于小波变换的场道脱空BP神经网络预测法

1.1基于小波变换的道面振动信号特征值提取

将任意在L2(R)范数空间中的信号f(t)在选定小波基下展开即为信号f(t)的连续小波变换，见式(1)。

Wf(a,b)==

(1)

式中：Wf(a,b)为连续小波变换系数，a为伸缩因子，b为平移因子。当a增大，则时窗伸展，频宽收缩，带宽变窄，中心频率降低，而频率分辨率增大。小波变换具有多分辨率特性，可以由粗到精地逐步观察信号。通过适当选择尺度和平移参数可以得到一个时频伸缩窗，只要选择合适的小波基函数，就可以使小波变换在时频域内表现信号的局部特征。

在小波变换中，每步分解只是对低频子空间，而高频子空间不分解，因而高频跨度较宽。在实际应用中，对信号的某些特定时间段或频率段的特征较感兴趣，因此希望在感兴趣的频率点上的频率分辨率较高，在感兴趣的时间点上的时间分辨率较高。小波包分析可更加精细的分析道面振动信号，它按多层次进行划分频带，同时对第一次分解得到低频成分与高频成分进一步再分解，每层小波包将信号原频带一分为二，3层小波包可将原频带分割为8个子频带，从而实现频带细分，提高频域分辨率。道面振动信号经过小波分解并选出最佳基后，将最佳基上的分解结果在时频面上表示，并且可以根据被分析振动信号的特征，自适应地选择相应的频带，使之与振动信号频谱相匹配，从而提高对振动信号的时频分辨率。利用小波变换可获得道面振动信号的分解特征值，作为场道脱空状况BP神经网络预测的评价依据。

1.2场道脱空的BP神经网络预测

BP神经网络通常含有一个或多个隐含层，一个典型的三层BP神经网络模型包含输入层、隐含层以及输出层共三层。BP神经网络可以实现从输入到输出的任意非线性映射。横向各层之间采用全互联的方式，纵向上不存在相互连接，隐含层可以是一层也可以是多层。下文通过小波变换处理后的加速度特征值作为BP神经网络的输入向量，对BP神经网络进行训练，利用BP神经网络的非线性映射能力，得到输入向量与输出向量间的变化规律。

利用室内试验，事先设定好道面脱空状况，通过施加冲击荷载获得不同脱空位置和无脱空位置的振动信号时程曲线。输入所获取的学习样本，通过设置好的网络结构和上一次迭代的权值和阈值，从神经网络的第一层向后计算各神经元的输出。然后，对获得的权值和阈值进行修正，从最后一层向前计算各层的权值和阈值对总误差的影响，据此对各层神经元的权值和阈值进行调整。通过逐层训练后获得学习样本的变化规律，然后通过机场场道现场测试对比加以验证。

2　室内模型试验

本试验在中国民航大学机场学院土木工程试验室进行(见图1)。为真实模拟机场道面振动响应信号，浇筑了规格为2 000 mm×800 mm×300 mm的混凝土板，由三块按机场道面尺寸制作的缩尺模型组成，板上有两条距板短边方向650 mm宽14 mm的嵌缝，板下设厚度为90 mm的砂土垫层并沿板四边向外拓宽约200 mm，垫层四周环绕黏土砖稳定垫层边缘以防砂土受振动后向四周塌散。振动信号采集设备采用江苏东华DV610竖向加速度传感器，采样频率500 Hz，传感器布置及测量方案见图2。

图1　室内模型试验图Fig.1　Indoor scaled model test

图2　室内模型试验测试方案Fig.2　Test scheme of indoor model experiment

如图2所示，在落锤击点周边设置10个东华DV610加速度传感器，分别编号为3-1,3-2,…,3-9,3-10。将传感器通过引线与信号采集器连接，并通过无线路由器与装有东华动态应变测试仪动态信号采集系统的笔记本连接。先进行无脱空工况的数据采集，然后分别在图2所示的虚线范围设置4个圆洞以模拟道面板的4个常见典型脱空区(见图3)，设定6组脱空对比试验工况(见表1)。通过在5种设定的高度(20 cm，40 cm，60 cm，80 cm和100 cm)自由下落施加冲击荷载模拟重锤式弯沉仪HWD(Heavy Weight Deflectometer)加载，实现五个级别冲击荷载对砂土垫层混凝土板在不同脱空工况下施加激励。

表1　室内脱空对比试验工况

图3　场道脱空模拟试验Fig.3　Pavement void simulation

3　试验结果分析

以3～10号传感器为例，对比分析无脱空工况与(板角)4区脱空下的道面竖向加速度时程信号，即对比分析spn103与spvd103。两对比脱空工况下振动信号存在差异，但无法直接获得振动信号隐含时频特征或直接判断道面脱空状况变化规律。选用小波函数为样条小波bior6.8，对其进行小波包变换，获得其经3层变换分解后小波包节点7～节点14的功率谱密度变化曲线(见图4和图5)。

图4　spn103工况下小波变换功率谱图Fig.4　Wavelet transform power spectrum of spn103

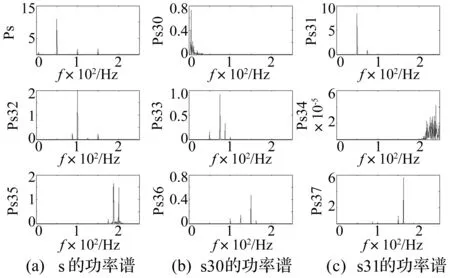
图5　spvd103工况下小波变换功率谱图Fig.5　Wavelet transform power spectrum of spvd103

3.1功率谱密度分析

图中的s30，s31，s32，…，s36，s37分别代表小波包节点7～节点14的功率谱密度变化曲线。从该图中可知终端各节点包含的道面振动频率成分和相应的幅值，以及节点重构信号的功率谱密度随频率变化。对比分析无脱空与脱空工况下道面振动信号经小波包分解终端各频带成分发现，无脱空信号各节点的频率成分的幅值除了节点13和节点14外均较脱空信号大，无脱空信号仅节点7和节点12频带宽度较脱空信号对应节点宽，其对应的频率成分幅值变化较缓。因而，可将道面振动信号的小波包分解后再对各小波包节点系数进行功率谱分析，不仅可以用于区分道面无脱空与脱空的差异，还可以通过两者差异频带进一步分析道面板无脱空与脱空工况下加速度信号振动特征，以此作为BP神经网络预测的训练特征。

3.2能量谱分析

以板角3～10测点振动信号小波分析为例，其采样频率是500 Hz，小波包分解选用小波函数为样条小波bior6.8，分解为1层～4层。故小波包分解将道面振动信号分别分解为2个，4个，8个，16个频带，根据采样定理，道面振动信号分析频率为250 Hz，每个频带宽度分别为125 Hz，62.5 Hz，31.25 Hz，15.625 Hz，图6和图7为三级落锤作用下道面振动信号在无脱空与板角脱空工况下的小波包能量分布。

图6　spn103工况下小波变换能量谱图Fig.6　Energy spectrum of wavelet transform of spn103

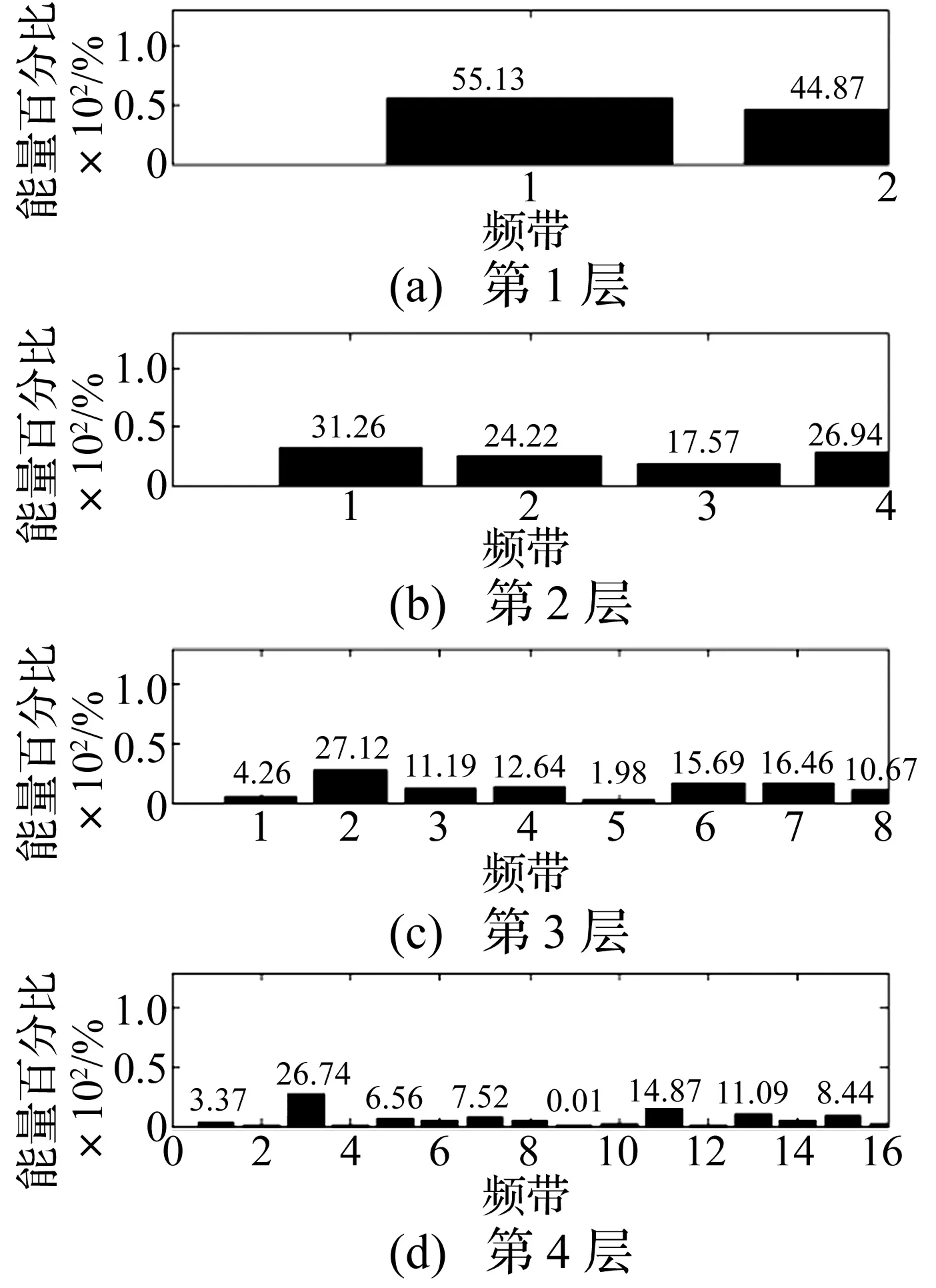
图7　spvd103工况下小波变换能量谱图Fig.7　Energy spectrum of wavelet transform of spvd103

由图6和图7可知，道面板在不同状态下的振动信号各层小波包能量谱分布存在显著差异。在三级荷载作用下，对比道面无脱空与脱空的能量谱图，当小波包分解一层时，前者能量谱值按频带号递增，后者按频带号递减，且前者低频带能量谱比例低于50%而后者高于50%。当小波包分解两层时，前者能量谱按频带号递增而后者则先减后增。当小波包分解三层时，两者能量谱变化趋势较一致。由图4、图5可知，道面振动信号频移范围(0～250 Hz)，每段31.25 Hz，从小至大排序：s30，s31，s33，s32，s36，s37，s35，s34的频谱，分别对应于图6、图7的频带编号1，2，4，3，7，8，6，5的能量谱。频移排序后的第三层能量谱见表2，对比分析发现：spn103的能量谱比例在低频段(0～93.75 Hz)较spvd103低，在较高频段(93.75～218.75 Hz)较spvd103高。表明脱空引起振动信号在低频段能量集中造成各频带能量比例上升，在高频段能量分散造成各频带能量比例下降。从而能量谱分析可以作为识别脱空引起信号差异和提取信号特征，故能量谱可作为BP神经网络分析的训练特征。

3.3时间-尺度分析

小波分解就是计算一系列振动信号和小波函数之间相似系数，相似程度越高则小波系数绝对值越大。因而，可通过小波系数反映信号特征。利用连续小波变换对道面竖向加速度时程信号进行时间-尺度分析，选定尺度因子a=50和3 000的连续小波系数分析结果进行比较，其中spn103与spvd103连续小波变换系数的三维网格图见图8。

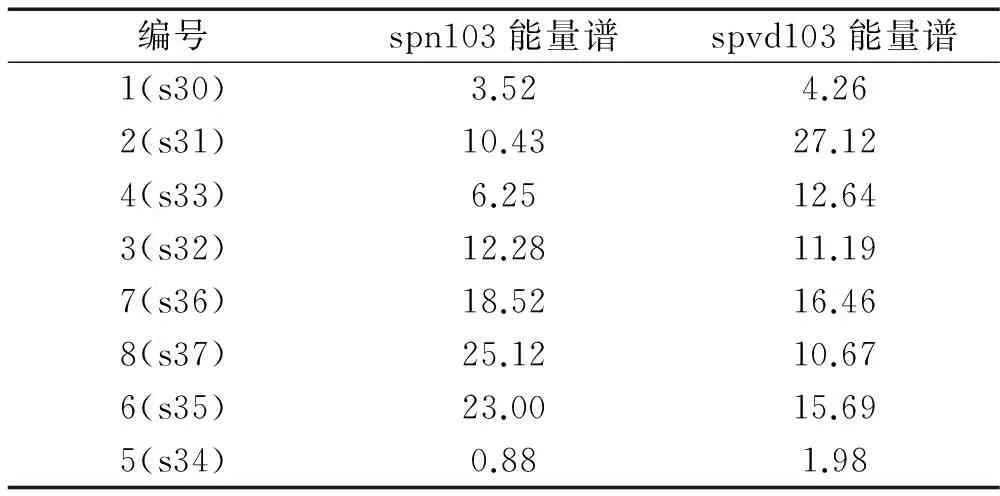
表2　排序后第三层能量谱

由图8可知，小波系数在三维网格图上的时间-尺度平面分布着类似地形图山脊的形状，称为小波脊线。通过脊线上小波系数值的起伏变化、脊线的位置可知信号的幅值大小与时间、频率的变化。在较低尺度(如a=50)下可分析信号较高频率成分，从中直观看出无脱空与板角脱空的小波系数幅值分布差异；在较高尺度(如a=3 000)下可分析信号较低频率成分，从图中看出小波幅值差异较大但小波系数分布近似。从而，可选定较小尺度作为BP神经网络预测的训练特征样本，不仅可减少计算量，还能识别轻微或中度脱空引起的信号差异。

(a) 尺度50 spn 103　　　　　　　　　　　　(b) 尺度50 spvd 103

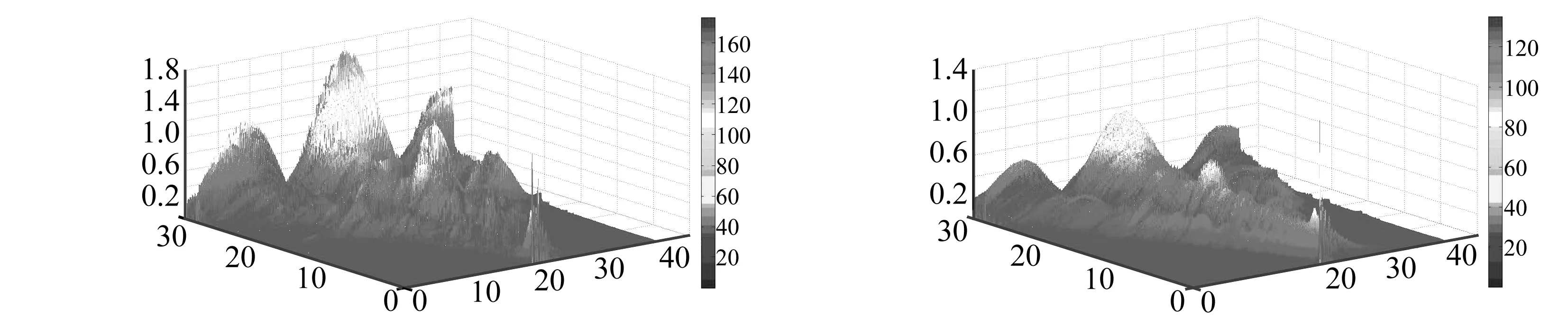
(c) 尺度3 000 spn 103　　　　　　　　　　　　(d) 尺度3 000 spvd 103图8　不同尺度范围下小波变换mesh图Fig.8　Mesh pictures of wavelet transform with different scales

3.4BP神经网络分析

根据前述试验及小波分析数据结果，选择1 500组输入向量作为训练样本，样本分为两类：脱空训练向量与非脱空训练向量，其中脱空训练向量的训练输出目标设定为0.9，非脱空训练向量的训练输出目标设定为0.1。SNORM输入向量的隐含层节点数取25，部分输入向量见表3。由于输出向量均≥0分别为0.1和 0.9。所以传递函数选择log-sigmoid函数。利用MATLAB中的BP神经网络工具箱及其函数进行编程，对输入向量进行训练和仿真，训练次数设定为200次，训练速率设定为0.01，训练精度设定为0.000 1。

BP神经网络训练结果见图9和图10。其中图9表示训练误差的正态分布图，由图中柱状图所示，误差为-0.056 76、0.023 91的数据量占大部分，且靠近期望值(即零误差线)，离期望值较远的数据量少，呈现出标准的正态分布特征，该图表示误差值小的数据占据总数据量的大部分，误差值大的数据占数据量的小部分，说明训练效果较好。图10为仿真后的预测输出和期望输出间的关系，将训练后的BP神经网络重新导入，将加速度特征值作为仿真输入向量，经过训练后的BP神经网络得到仿真输出向量，利用plot绘图函数将仿真输出向量和期望输出向量绘制在同一张图中，从图10可知，大部分的仿真输出向量都接近期望输出向量，只有极少部分的仿真输出向量偏离期望输出向量，说明训练效果较好。

表3　部分训练向量数据表

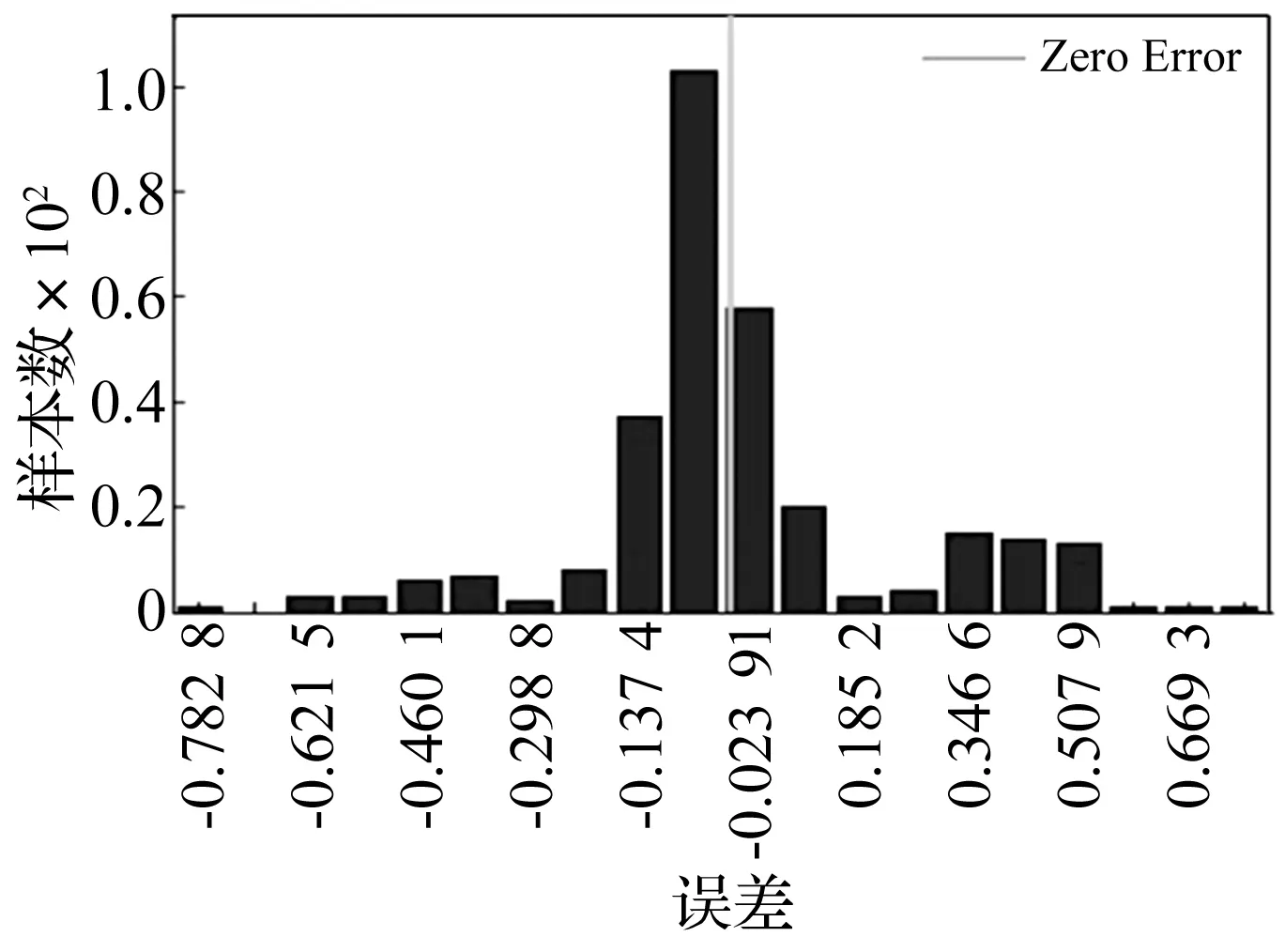
图9　训练误差正态分布图Fig.9　The training error of normal distribution

图10　预测输出和期望输出间的关系Fig.10　The relationships between the predicted output and the expected output

3.5机场实测验证

通过对某沿海机场进行现场实测(见图11)，利用重锤式弯沉仪Dynatest8081在机场道面施加多级冲击荷载激发跑道道面振动，利用基于小波变换的场道脱空BP神经网络预测法进行跑道道面脱空状况预测并在疑似脱空位置进行原地取芯加以对比(见图12)。

图11　某机场实地测试现场图Fig.11　An airport field test site map

图12　现场道面钻芯图Fig.12　Site sample of pavement bore hole

采用江苏东华无线采集系统DH5908配合DV610加速度传感器采集道面竖向加速度振动信号，通过室内试验结果训练BP神经网络，其对道面脱空状况的预测结果见图13，误差分析见图14。

图13　测试结果的期望关系图Fig.13　Expected diagram test results

图14　误差分析图Fig.14　Error analysis chart

由图13和图14可知，脱空期望输出向量为0.9，非脱空期望输出向量为0.1，仿真输出向量集中在0.2附近，即表明道面大部分呈弱脱空状态，仅部分测点位置出现了中度和重度脱空趋势。通过与现场取芯(见图12)的现场实测结果对比分析可知，所得BP神经网络预测结论准确可靠，即基于小波变换的场道脱空BP神经网络预测法具有较精确的预测道面脱空能力。

4　结　论

(1) 对道面振动信号进行功率谱分析可以识别道面无脱空与存在脱空的信号，并可通过两者频带差异进一步区分脱空的振动信号特征。

(2) 能量谱分析时，从道面振动信号的低高频段能量谱比例变化和能量谱按频带号变化趋势两方面可以作为区分场道脱空与否的特征，能快速定性判断场道基础健康状况。

(3) 时间-尺度分析能直观显示小波系数大小、分布及小波脊走向，从而敏锐反应道面脱空程度对道面振动信号处理结果的影响，可作为判断道面脱空状况的有效依据之一。

(4) 利用室内模型试验获得的特征向量组训练BP神经网络得到的分析模型，很好的预测了机场道面实测结果，并与道面钻芯查看结果相一致，为场道脱空状况的快速无损测试提供了技术方案，值得进一步研究。

[1] HUANG M H,THAMBIRATNAM D P. Dynamic response of plates on elastic foundation to moving loads[J]. Journal of Engineering Mechanics, 2002, 128(9):1016-1022.

[2] 李洪泉, 董亮, 吕西林. 基于小波变换的结构损伤识别与试验分析[J]. 土木工程学报, 2003, 36(5):52-57.

LI Hongquan, DONG Liang, LÜ Xilin. Identification of structural damage and test study based on wavelet transform[J]. China Civil Engineering Journal,2003,36(5):52-57.

[3] 陈仕龙, 张杰, 毕贵红,等. 基于小波分析的特高压直流输电线路双端电压暂态保护[J]. 电网技术,2013,37(10):2719-2725.

CHEN Shilong, ZHANG Jie, BI Guihong, et al. Wavelet analysis based two-terminal transient voltage protection for UHVDC transmission lines[J]. Power System Technology,2013, 37(10):2719-2725.

[4] 章浙涛, 朱建军, 匡翠林,等. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报,2014,43(1):13-20.

ZHANG Zhetao, ZHU Jianjun, KUANG Cuilin, et al. Multi-threshold wavelet packet de-noising method and its application in deformation analysis[J]. Acta Geodaeticaet Cartographica Sinica, 2014, 43(1):13-20.

[5] 叶玮琳, 郑传涛, 王一丁. 基于TDLAS的红外湿度检测中的小波去噪试验研究[J]. 光电子·激光,2013,24(1):104-111.

YE Weilin, ZHENG Chuantao, WANG Yiding. Experimental research on wavelet denoising in infrared humidity detection based on TDLAS technique[J]. Journal of Optoelectronics·Laser, 2013, 24(1): 104-111.

[6] 孙磊, 慕玉坤, 郝宪武.基于小波变换和ARIMA模型的桥梁健康监测数据分析[J]. 中外公路,2015,35(1):126-130.

SUN Lei, MU Yukun, HAO Xianwu. Analysis of bridge health monitoring data based on wavelet transform and arima model[J]. Journal of China & Foreign Highway,2015,35(1): 126-130.

[7] 李保琦, 周泽江, 马妍博. 基于小波神经与随机分析的径流预测[J]. 西北农林科技大学学报(自然科学版), 2014, 34(11):169-174.

LI Baoqi, ZHOU Zejiang, MA Yanbo. Runoff forecasting based on wavelet analysis, artificial neural network and hydrologic frequency analysis[J]. Journal of Northwest A&F University(Natural Science Edition), 2014, 34(11):169-174.

[8] 卢正, 姚海林, 胡智. 基于车辆-道路结构耦合振动的不平整路面动力响应分析[J]. 岩土工程学报,2013,35(1):232-238.

LU Zheng, YAO Hailin, HU Zhi. Dynamic response analysis of rough pavement under vehicle-road system coupled vibration[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 232-238.

[9] MAIER H R, DANDY G C. Neural networks for the prediction and forecasting of water resources variables: a review of modeling issues and applications[J]. Environmental Modeling and Software, 2000, 15(1):101-124.

[10] MULETA M K, NICKLOW J W. Joint application of artificial neural networks and evolutionary algorithms to watershed management[J]. Water Resources Management, 2004, 18(5): 459-482.

[11] NASH J E, SUTCLIFFE J V. River flow forecasting through conceptual models: Part I-A discussion of principles[J]. Journal of Hydrology,1970, 125: 277-291.

[12] 崔东文. 多隐层BP神经网络模型在径流预测中的应用[J]. 水文, 2013, 33(1):68-73.

CUI Dongwen. Application of hidden multilayer BP neural network model in runoff prediction[J]. Journal of China Hydrology, 2013, 33(1): 68-73.

[13] 杨发群, 邱卫宁, 魏成,等. 顾及不确定因素的GA-BP神经网络在路基沉降预测中的应用[J]. 测绘工程, 2013, 22(6):51-54.

YANG Faqun, QIU Weining, WEI Cheng, et al. Application of GA-BP neural network with uncertainties to the subgrade settlement prediction[J]. Engineering of Surveying and Mapping, 2013, 22(6): 51-54.

[14] 于伟, 蔡璟珞, 安凤平. 边坡位移LMD-BP神经网络模型研究[J]. 计算机应用与软件, 2013, 30(9):107-109.

YU Wei,CAI Jingluo, AN Fengping. Study on slope displacement prediction model based on LMD-BP neural network[J]. Computer Applications and Software,2013,30(9): 107-109.

[15] 彭永恒, 任瑞波, 罗跃纲,等. 刚性路面脱空声识别集成神经网络方法[J]. 中南公路工程, 2005, 30(3):15-18.

PENG Yongheng, REN Ruibo, LUO Yuegang,et al. Void acoustic identifying of rigid pavement based on integrated neural network[J]. Journal of Central South Highway Engineering, 2005, 30(3):15-18.

[16] 刘海平, 刁延松. 基于小波包分析与BP神经网络的结构损伤检测研究[J]. 工程建设, 2013, 45(4):13-16.

LIU Haiping, DIAO Yansong. Study on the structural damage identification based on wavelet packet and BP neural network[J]. Engineering Construction, 2013, 45(4):13-16.

Back propagation neural network applied in the prediction of pavement void based on wavelet transform method

LIU Guoguang1, WU Zhiwei1, LIU Zhiyong2, CHENG Guoyong1

(1. Airport College of Civil Aviation University of China, Tianjin 300300, China; 2. ZGSZ, Shenzhen 518128, China)

Pavement void is one of the important parameters of influencing airport operation safety. In order to achieve the non-destructive test of the pavement void, a back propagation prediction method on the basis of wavelet transform was proposed. By virtue of indoor model tests, an impacting load was imposed on a scaled pavement model and vertical acceleration signals of the pavement were measured, which were then used to achieve the power spectrum analysis, energy spectrum analysis and time-scale analysis by wavelet transform method. A back propagation(BP) neural network was trained by 1500 sets of feature vectors indicating different pavement void conditions in order to improve the prediction function. A site experiment of airport pavement was conducted and pavement concrete samples were drilled to validate the reliability of BP neural network prediction. The results show that pavement vibration signals can reflect the dissipative effects of energy transmission in void area. There are significant differences between complete void and half void areas, which can be shown by regular patterns. The results of site experiment are in good agreement with the prediction of BP neural network trained by the indoor test results, and the signals of slight void are obviously distinguishable, by which the reliability and feasibility of the method in pavement void evaluation are proved.

pavement engineering; pavement void; wavelet transform; back propagation neural network

国家自然基金面上项目(51178456);中央高校基本科研业务费中国民航大学专项资助(312016D019)；中国民航大学青年骨干教师项目

2015-05-13修改稿收到日期：2015-09-16

刘国光 男，硕士，讲师，1980年生

程国勇 男，教授，1971年生

E-mail：14660989@qq.com

TU393.3

A DOI:10.13465/j.cnki.jvs.2016.14.033