1种基于复合形法的改进遗传算法
毕馨文,解成俊,张泽梁
(1.北华大学信息技术与传媒学院,吉林 吉林 132013;2.北华大学计算机科学技术学院,吉林 吉林 132021)
1种基于复合形法的改进遗传算法
毕馨文1,解成俊2,张泽梁1
(1.北华大学信息技术与传媒学院,吉林 吉林132013;2.北华大学计算机科学技术学院,吉林 吉林132021)
提出了1种基于复合形法的改进遗传算法,分析该算法与遗传算法相结合的思想和流程;通过算法测试函数Rosenbrock测试改进的算法;通过与常规算法的对比,验证该传算法的优越性,并将该算法应用到一种间歇反应器的温度优化问题中.该算法可为常规的单目标或多目标优化问题提供借鉴.
复合形法;遗传算法;优化;间歇反应器
【引用格式】毕馨文,解成俊,张泽梁.1种基于复合形法的改进遗传算法[J].北华大学学报(自然科学版),2016,17(5):693-697.
近年来,由于遗传算法(GeneticAlgorithm,GA)和差分进化(DifferentialEvolutionAlgorithm,DEA)算法等基于种群的随机优化方法能够有效地提供全局优化解,因此受到了广泛关注[1-3].遗传算法一般应用于单目标或多目标优化问题,与基于梯度的算法相比计算更为复杂,因此比较适合复杂的函数计算或者离线分析.GA可以是二进制代码,种群数量的真实值用(0,1)编码,通常在GA中分为4个步骤:初始化、选择、交叉和变异.在初始化时随机选择生成种群,初始种群均匀分布在解空间.种群内的多个个体通过重组或者变异来增加种群的多样化,最后获得较好的子代.在每一代GA中,变异和交叉算子用于增加种群多样性,生成的子代与母代相比具有更好的适应度函数值,所选择的母代个体与生成的子代一起进入下一次循环,直至得到最佳的全局解.
目前,在优化问题上,已经有很多种改进策略来增加GA全局最优解的收敛性和收敛率,一般是单步改进或者多步改进.选择种群的常用方法有轮盘赌、随机残余轮盘赌、随机均匀采样、厌恶选择或锦标赛选择.Goldberg等[4]在基准优化问题上研究了不同的选择方法;Wu等[5]比较了各个交叉策略;Herrara等[6]研究了真实参数交叉与变异,已存在的交叉算子有线性、单纯、混合、伪二进制、模糊重组等[7];Kasat等[8]应用跳跃基因(jumpinggenes,JG)概念对二进制代码NSGA-II进行了多目标优化;Guria等[12]进一步修正了二进制编码的跳跃基因,后来改进的跳跃基因方法被应用于许多工程问题;Ripon等[13]提出了1种实部编码跳跃基因遗传算法,该方法比常规的遗传算法多了额外的交叉和变异步骤,与二进制编码的跳跃基因遗传算法有相同的效果,然而额外的交叉和变异步骤使得各自的优化结果更好,更适合解决单目标和多目标优化问题.复合形法是由Box提出的一种多起点约束优化算法,这种算法相比GA对于小种群具有更好的收敛性,但更容易陷入局部收敛.本次研究利用复合形法改进传统的GA来增加收敛效率,同时在进化过程中增加了新个体,称为复合形个体,并在验证改进算法性能时与传统GA及JGGA进行对比.
1 基于复合形法的改进遗传算法
遗传算法的原理是模仿生物进化“适者生存”的基本思想,通过创建初始种群,然后交叉、变异形成新的个体.适应能力强的个体进入到下一代中,能力弱的被淘汰[9],而确定种群大小是算法迭代的重要环节,种群过小容易导致算法陷入局部收敛;种群过大则计算时间大大增加.复合形法是一种多起点优化方法,由约束优化问题的单纯形法衍变而来[10].
1.1改进遗传算法流程
复合形法对于小种群的收敛效率优于其他方法,但是也存在局部收敛问题,为了解决这类问题,本文提出将复合形法用于GA的全局搜索来改进GA.在每一代中由复合形法创造出1个或者多个新个体,然后与每一代适应度函数值中较差的个体对比,如果复合形法产生的个体优越则取代之前适应度函数值较差的个体,否则继续循环.
本文基于复合形法改进的遗传算法流程见图1,步骤如下:
1)初始化.定义系统参数,如变量的数量和边界、迭代次数、交叉算子和变异算子;
2)生成初始种群.生成满足约束条件的初始种群,计算初始种群的适应度函数值;
3)交叉与变异.在交叉算子和变异算子满足时执行;
4)计算适应度函数值.计算交叉与变异后生成子代的适应度函数值;
5)选择精英.在目前所有个体中选择适应度较好的,准备进入下一代;
6)生成复合形成员.生成复合形成员,然后进行对比;
7)循环,直至结束.
1.2复合形成员的生成策略
复合形法是一种确定性的多起始优化算法,在此方法中,复合数学图形在n个搜索空间方向通过选择至少n+1个点来生成.复合形的移动方向变得更加灵活,每一次搜索到新的复合形顶点满足约束条件后才可以替代上一次搜索的结果[14].新的点通过保留复合形顶点的面心在一个特殊化的距离内形成:
P新=(1+α)P面心-αP上一顶点,
其中:P新为生成新的复合形成员;P面心为包括上一个被替代的复合形成员在内的复合形的面心,由包括上一个被替代的复合形成员在内的复合形成员的算数平均值得到;P上一顶点为被替代的上一个复合形成员,可以通过种群成员的目标函数值来直接得到.
如果生成的新的复合形成员不满足1个或者多个边界约束,则将新的复合形成员的值就近变化为距离此点最近的满足全部约束条件的点,在这种情况下,如果新的复合形成员比上一个即将被替代的复合形成员更好,则进行替换;反之则保留上一个被替代的复合形成员而忽略新的复合形成员[15].
本次研究中,在遗传算法的每一代迭代过程中,复合形都是由种群中n个最好的成员来生成,较差的成员在复合形面心方向投影,其中α=0.8.所形成的成员如果优于之前的成员,则进行替代;反之依然保留上一个成员.
2 优化控制问题
本文采用著名的算法测试函数Rosenbrock对基于复合形法测试改进的遗传算法[11],同时与JG法、常规GA法及复合形法(CB)进行对比,验证改进算法的优越性.Rosenbrock函数表示为

4种方法优化测试函数的结果见图2.由图2可以看到:基于复合形法改进的遗传算法收敛精度和效率最好.
近年来,化工生产中常见的间歇反应器一般是按照批量进行反应,在优化问题上较受关注.Edgar等[16]对间歇反应器的反应流程A-B-C进行了研究,并利用准牛顿方法发现了最佳温度策略来使成分B产量最大化;Pham等[17]也对此问题进行了研究.间歇反应器的过程模型
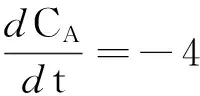
(1)
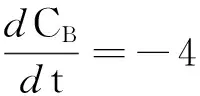
(2)
采用控制向量参数化的方法将间歇反应器的温度数据离散化为5个间隔,然后在6个离散点中寻找最优温度值.利用本文基于复合形法改进的遗传算法进行间歇反应器的温度优化,结果见图3.
由图3可以看出:在估计方程数量为200时,GA和JG的收敛速度更快一些,但是之后基于复合形法改进的遗传算法就开始占据优势.在最终的结果中,常规的GA最佳值为0.611 340,CB为0.611 388,JG为0.611 394,而基于复合形法改进的遗传算法最佳值为0.611 397.
3 结 论
遗传算法自提出以来已被广泛应用于各个领域,其中对单目标或多目标优化问题的应用比较成功,但遗传算法自身收敛效率不高且容易陷入局部收敛,目前已有了很多改进的策略.本文提出了1种基于复合形法改进的遗传算法,通过测试验证了该改进算法的优越性,并通过一个间歇反应器实例证明了其实用性.该改进算法可为单目标或者多目标优化问题提供借鉴.
[1]DGoldberg.Geneticalgorithmsinsearch,optimization,andmachinelearning[D].Boston:Addison-WesleyProfessional,1989.
[2] 刘月凡,朱星.改进的遗传算法求解柔性作业车间调度问题[J].大连交通大学学报,2015,36(4):101-104.
[3] 刘桂英,山传文.一种基于遗传算法的多模型预测控制方案[J].北华大学学报(自然科学版),2014,15(4):557-560.
[4]DEGoldberg,KDeb.Acomparativeanalysisofselectionschemesusedingeneticalgorithms[J].FoundationsofGeneticAlgorithms,1991,44(3):69-93.
[5]SJWu,PTChow.Steady-stategeneticalgorithmsfordiscreteoptimizationoftrusses[J].Computers&Structures,1995(56):979-991.
[6]FHerrera,MLozano,JLVerdegay.Tacklingreal-codedgeneticalgorithms:operatorsandtoolsforbehaviouralanalysis[J].ArtificialIntelligenceReview,1998(12):265-319.
[7]KDeb.Multi-objectiveoptimizationusingevolutionaryalgorithms[M].NewYork:JohnWiley&Sons,2001.
[8]HMPandey,AChaudhary,DMehrotra.AcomparativereviewofapproachestopreventprematureconvergenceinGA[J].AppliedSoftComputing,2014(24):1047-1077.
[9] 朱大林,詹腾.基于元胞多目标遗传算法的蜗杆优化设计[J].计算机工程与应用,2015,51(13):263-270.
[10] 杨兰兰,屠彦,温佳佳,等.复合形法在PDP计算机仿真中的应用[J].光电子技术,2009,29(3):149-153,160.
[11]HHRosenbrock.Anautomaticmethodforfindingthegreatestorleastvalueofafunction[J].TheComputerJournal,1960(3):175-184.[12]CGuria,PKBhattacharya,SKGupta.Multi-objectiveoptimizationofreverseosmosisdesalinationunitsusingdifferentadaptationsofthenon-dominatedsortinggeneticalgorithm(NSGA)[J].Computers&ChemicalEngineering,2005(29):1977-1995.
[13]KSNawazRipon,SKwong,KFMan.Areal-codingjumpinggenegeneticalgorithm(RJGGA)formultiobjectiveoptimization[J].InformationSciences,2007(177):632-654.[14] 徐量,张勤.基于GA-BP神经网络的隧道初期支护钢拱架内力预测[J].北华大学学报(自然科学版),2012,13(6):717-721.
[15] 董倩.改进遗传算法优化模糊均值聚类中心的图像分割[J].吉林大学学报(理学版),2015,53(4):680-686.
[16]TFEdgar.Optimizationofchemicalprocesses[M].2nded.NewYork:McGraw-Hill,2001.
[17]SADadebo,KBMcauley.Dynamicoptimizationofconstrainedchemicalengineeringproblemsusingdynamicprogramming[J].Computers&ChemicalEngineering,1995,19:513-525.
【责任编辑:郭伟】
Improved Genetic Algorithm Based on Box ComplexforOptimalControlProblem
Bi Xinwen1,Xie Chengjun2,Zhang Zeliang1
(1.School of Information Technology and Media,Beihua University,Jilin 132013,China;(2.Computer Science and Technology,Beihua University,Jilin 132021,China)
Animprovedgeneticalgorithmbasedonboxcomplexmethodwasproposed,theideaandprocessfortheboxcomplexmethodcombinedwithgeneticalgorithmwereanalyzed,andthentheimprovedalgorithmbyfamoustestfunctionofRosenbrockalgorithmwastested,thesuperiorityofimprovedgeneticalgorithmwasvalidatedbycontrastwiththeconventionalalgorithm,andthenitwasappliedtoabatchreactortemperatureoptimization.Theimprovedalgorithmcanprovideareferenceforconventionalsingle-targetormulti-objectiveoptimizationproblem.
boxcomplex;geneticalgorithm;optimization;batchreactor
1009-4822(2016)05-0693-04
10.11713/j.issn.1009-4822.2016.05.030
2016-04-02
国家教育部春晖计划项目(104900150);国家自然科学基金项目(61072111);吉林省科技发展计划项目(20140101206JC-16).
毕馨文(1983-),女,硕士,讲师,主要从事计算机应用技术研究,E-mail:52600613@qq.com.
TN911.73
A

