科赫雪花上的振动模式
邱为钢
(湖州师范学院 理学院,浙江 湖州 313000)
科赫雪花上的振动模式
邱为钢
(湖州师范学院 理学院,浙江 湖州313000)
数值计算得到了科赫雪花上的本征振动模式图形. 讨论了本征振动频率分布规律和振动图形的对称性.
科赫雪花;振动模式
圆形鼓振动产生声音,声音的特征频率理论上是拉普拉斯算符在圆形区域上满足第一类边界条件的本征值. 文献[1]讨论了等边三角形、等腰直角三角形等形状上的特征频率及其振动模式. 这些区域具有点群对称性,周长有限,本证频率和振动模式有解析表达式. 分形区域则具有自相似性,周长无限但面积有限,只能用数值方法求解本征值. 同时具有点群对称性和自相似性的分形物体是科赫雪花[2],文献[3]、[4]用数值方法计算得到了科赫雪花上的本征振动频率和图形,所用方法有所区别,文献[3]用的是专门设计的程序包,而文献[4]用的是Mathematica软件. 从教学实际出发,大部分师生熟悉的是Mathematica软件. 我们借用文献[6]的思路和方法,利用Mathematica软件,数值计算科赫雪花上的前6个本征振动模式,讨论这些本征模式的对称性,以及本征频率的分布规律.
1 科赫雪花及对称性
科赫雪花操作如下,先从一个正三角形开始,每一条边的中点向外作一个等边三角形,边长是原来边长的三分之一.然后把等边三角形的底边去掉,再对每一条边作同样的操作,依次叠代下去,直至无穷,最终得到的图形就是科赫雪花. 图1是零到三次叠代操作的图形,以科赫雪花的中心为原点,所在平面为Oxy平面. 由图1可以看出,科赫雪花具有以下对称性: 旋转对称性,绕z轴转动π/3的整数倍;反射对称性,对Oxz平面和Oyz平面的反射对称性;前面两种基本对称性的组合.
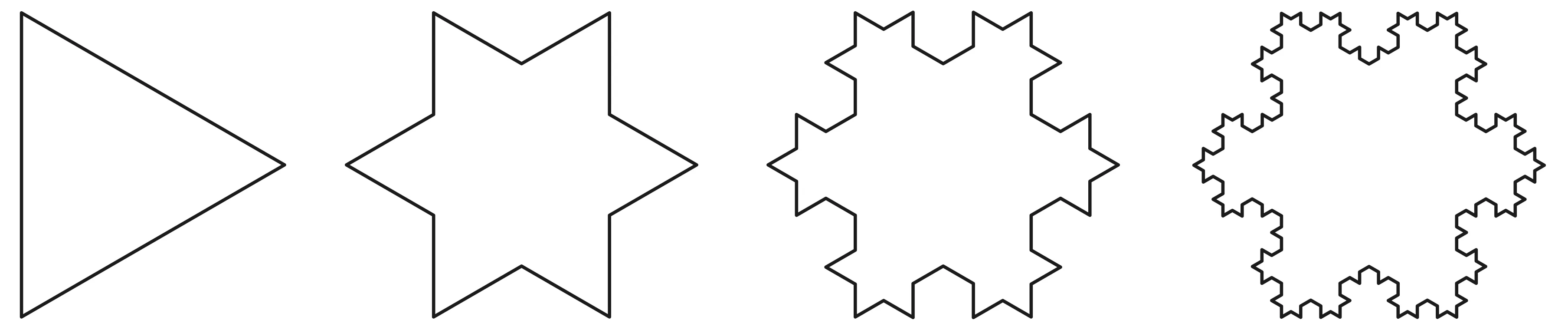
图1 科赫雪花零级到三级近似
2 拉普拉斯算符的离散化
数值求解拉普拉斯算符本征值问题,一般采用离散化方法. 先用合适的网格剖分区域,设标记为(m,n)的格点上的函数值为um,n,这个格点最邻近的4个函数值分别为um+1,n,um-1,n,um,n+1,um,n-1. 设格点间距是a,于是离散化的本征值方程是
um+1,n+um-1,n+um,n+1+um,n-1-4um,n=λaum,n
(1)
考虑到所有的点以及边界条件,并把二维标记(m,n)按顺序编号,式(1)化为矩阵形式的本征方程:
Lu=λau
(2)
其中L是拉普拉斯矩阵,矩阵元可以从式(1)中读出. 这样,本征值和本征函数就可以利用Mathematica内置函数来求解.对于科赫雪花,并没有采用常用的正方形网格剖分,而是正三角形剖分,更好地保持对称性. 具体的网格剖分和拉普拉斯矩阵,请参考程序.
3 本征振动模式及对称性
考虑到篇幅和计算量,我们只给出前6个本征振动模式的三维图和等高线图,如图2—图7所示.
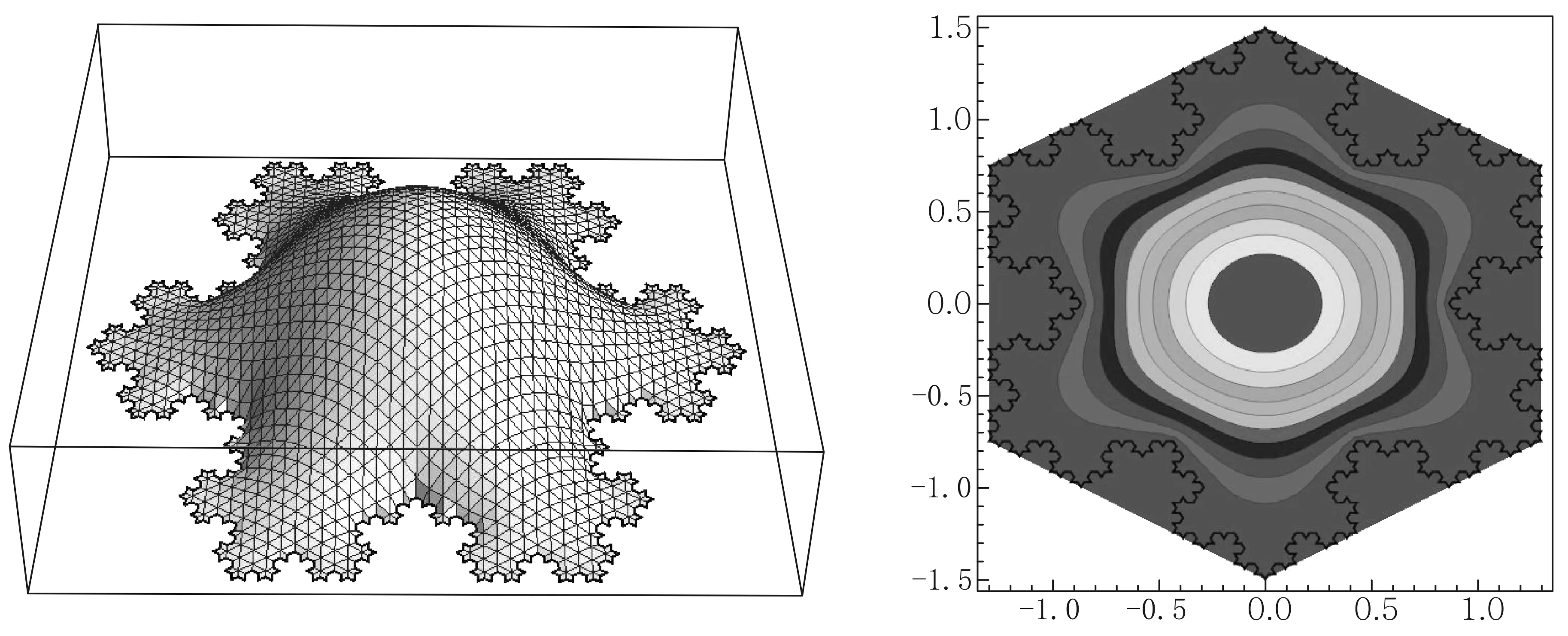
图2 第一本征振动模式三维和等高线图

图3 第二本征振动模式三维和等高线图
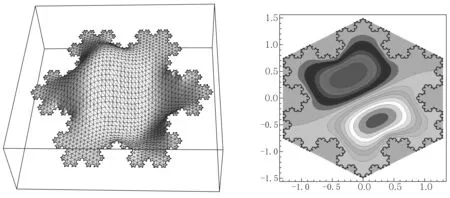
图4 第三本征振动模式三维和等高线图

图5 第四本征振动模式三维和等高线图

图6 第五本征振动模式三维和等高线图

图7 第六本征振动模式三维和等高线图
由图2—图7可以看出,第一和第六模式保持科赫雪花的所有点群对称性. 数值计算发现,第二和第三模式是简并的,即它们具有相同的本征频率;第二和第三模式只保持部分对称性,及一种镜面反射对称性;第四和第五模式也是简并的,保持两种镜面反射对称性.
4 本征值分布
设k是本征波矢量k2=λ,N(k)是波矢量小于k的本征模式数目(含简并),当波矢量k趋向无穷时,本征模式数目函数N(k)的渐近行为满足Weyl-Berry定律[5]:
(3)
其中D是区域的维数,MD是区域的测度(体积或面积),d是区域边界的维数,mD是区域边界的测度(面积或长度). 如果是严格的科赫雪花,即近似阶数趋向无穷,那么科赫雪花内部区域的维数D=2,边界的维数是d=ln4/ln3=1.261 86. 本文中的零级近似正三角形的边长是1,科赫雪花取到四级近似,此时它的面积是A=0.67,周长是l=9.48. 如果不把四级近似的科赫雪花看作分形物体,而是一个多边形,那么按照式(3),本征模式数目分布是
Np(k)~0.055k2-0.189k
(4)
如果把四级近似的科赫雪花看作分形物体,边界维数取为d,则本征模式数目分布是
NS(k)~0.055k2-0.213kd
(5)
由于计算条件制约,我们只考虑前220个本征波矢量,此时本征模式数目函数N(k)如图8所示.
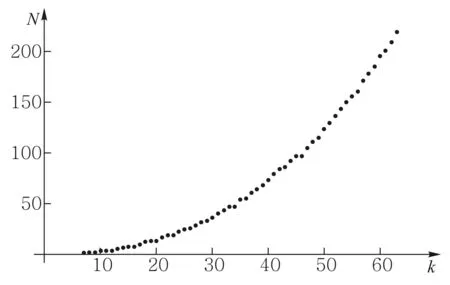
图8 四级近似科赫雪花上本征模式数目函数
由图8中得数据拟合得到的本征模式数目函数,如果把四级近似科赫雪花看作是多边形,拟合公式是
Np(k)~0.073k2-1.345k
(6)
如果把四级近似科赫雪花看作是分形物体,拟合公式是
NS(k)~0.081k2-0.605kd
(7)
式(4)和式(6)误差较大,式(5) 和式(7)误差较小,这说明四级近似的科赫雪花边界具有分形特性,不是一般的多边形.
5 结论
我们对四级近似的科赫雪花进行正三角形网格剖分,数值求解,得到了离散化后的拉普拉斯算符的本征函数和本征值,画出了科赫雪花上的前6个本征振动模式. 这些模式,完全或部分保持了科赫雪花原有的对称性. 数值计算得到了前220个本征波矢量的数目函数,拟合公式表明,科赫雪花的边界具有分形特性.
[1]呼格吉乐,邱为钢. 振动模式的可视化[J]. 大学物理,2010,29(06):40-42.
[2]科赫雪花[EB/OL]:http://mathworld.wolfram.com/KochSnowflake.html
[3]LapidusML,NeubergerJW,RenkaRJ,etal.Snowflakeharmonicsandcomputergraphics:numericalcomputationofspectraonfractaldrums[J].InternatJBifurcChaosApplSciEng,1996,6 (7):1185-1210.
[4]McClureM.VibrationoftheKochdrum[J].MathEducRes,2007,12: 149-161.
[5]BerryM.StructuralStabilityinPhysics[M].Berlin:Springer-Verlag,1979: 51-53.
ThevibrationalmodesofKochsnowflakes
QIUWei-gang
(SchoolofScience,HuzhouTeachersCollege,Huzhou,Zhejiang313000,China)
TheeigenvibrationmodesofKochsnowflakearedrawnfromnumericalsolutions.Thesymmetriesofthesemodesanddistributionofwave-vectorarediscussed.
Kochsnowflake;vibrationalmodes
2015-02-25;
2015-05-19
国家自然科学基金(11475062,11275067)、湖州师范学院中青年教师卓越教学能力培养计划专题项目(2014ZYJH017)资助
邱为钢(1975—),男,江苏张家港人,湖州师范学院理学院副教授,博士,主要从事大学物理的教学和研究工作.
教学讨论
O411;O441
A
1000- 0712(2016)01- 0007- 04

