多点测量法与最小偏向角法在色散特性测量中的比较分析
张奕雄
(韩山师范学院 物理与电子工程系,广东 潮州 521041)
多点测量法与最小偏向角法在色散特性测量中的比较分析
张奕雄
(韩山师范学院 物理与电子工程系,广东 潮州521041)
探讨入射角、偏向角关联函数上有利区域的多点测量法,在获取这些非最小偏向角的测量数据后,进行最小二乘法的非线性拟合,得到对应入射光线波长的介质的折射率,从而可对系列谱线的折射率进行色散方程拟合,进而,其拟合结果的不确定度与通常采用的最小偏向角方法实现的色散方程拟合的参数不确定进行比较.实验表明,多点测量拟合法可获得拟合量的较小相对误差及较高相关系数,多点测量法可作为一种高精度测量介质折射率及色散特性的补充方法.
多点测量拟合法; 最小偏向角; 折射率; 非线性拟合;色散特性;
实验获取介质的色散特性曲线多为采用最小偏向角测量的方法[1,2],利用测得的系列谱线的折射率,进行介质色散方程的最小二乘法拟合.而最小偏向角的精确临界位置判断的不准,会引入一定的误差[3],难于满足高精度测量要求.本文提出多点测量拟合法,选择避开入射角与偏向角所成的函数曲线变化率近零区域及极值的测量不利区域,进行系列入射角、偏向角的可靠位置测量,并实现其最小二乘法的入射角、偏向角函数关系拟合,从而获得对应入射波长的介质折射率,进而获得色散特性测量的较小实验误差,满足高精度测量要求.
1 最小偏向角方法获取介质的色散方程
当波长为λ的光线从三棱镜的侧面以入射角i1入射折射率为n、顶角角度为A的三棱镜后,产生折射角γ1的折射,当折射光线传播到棱镜的另一面时,以入射角i2入射,折射角γ2出射棱镜,光线从入射棱镜到出射棱镜发生了偏向角δ角度的偏转.由折射定律可得
sini1=nsinγ1及nsini2=sinγ2
(1)
由三棱镜及入射光线、出射光线的几何关系可得[1,4,5]
δ=(i1-γ1)+(i2-γ2)=i1+γ2-A
(2)
为了得到入射角、偏向角及折射率的关系,γ2用入射角及折射率表示
(3)
式(3)即为入射角、偏向角及折射率的函数关系式.
选定样品棱镜后,其顶角为一定值A,对于入射波长λ的光线,其折射率为定值n,由入射角与偏向角的关系可知,存在最小偏向角δmin,通常测得δmin后依据折射率与最小偏向角的关系[1,3]可求得样品折射率:
(4)
在不同实验环境测得系列谱线对应的最小偏向角的二组数据,表1为第一组测量数据、表2为第二组测量数据.

表1 不同波长对应的最小偏向角及利用式(6)计算的样品折射率(第一组测量数据)

表2 不同波长对应的最小偏向角及利用式(6)计算的样品折射率(第二组测量数据)
柯西色散方程中折射率与波长有如下关系[1,6]:
(5)
而指数衰减式中折射率与波长的关系[2]为
n=Be-λA-1+C
(6)
利用origin软件的自定义非线性拟合功能,再利用式(5)和(6)进行系列谱线色散方程的最小二乘法拟合[7-10],得到测量的第一组及第二组数据所拟合的柯西色散方程和指数衰减方程的参量分别如表3、表4所示,所拟合出的柯西色散方程曲线分别如图1、图2所示.
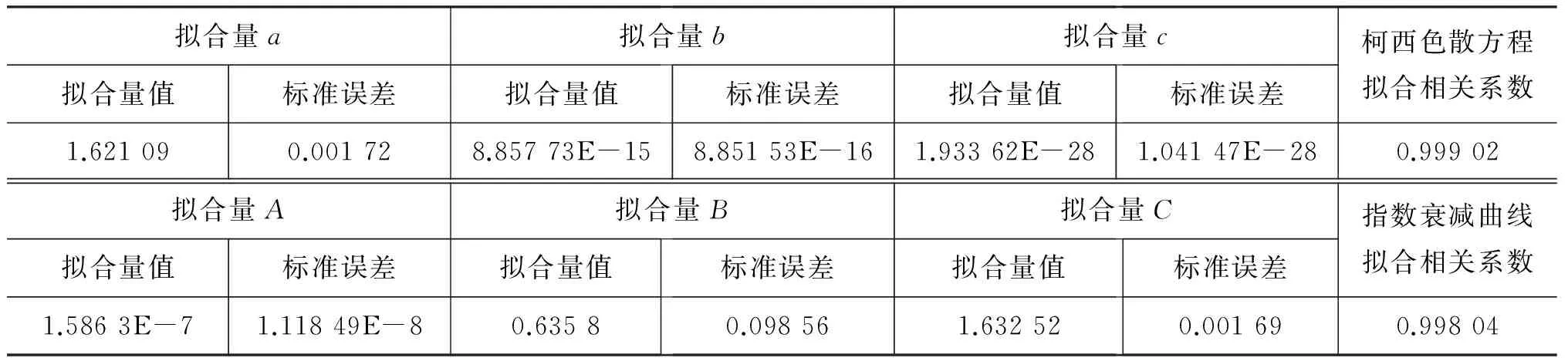
表3 最小偏向角法测得第一组折射率数据的色散方程拟合结果
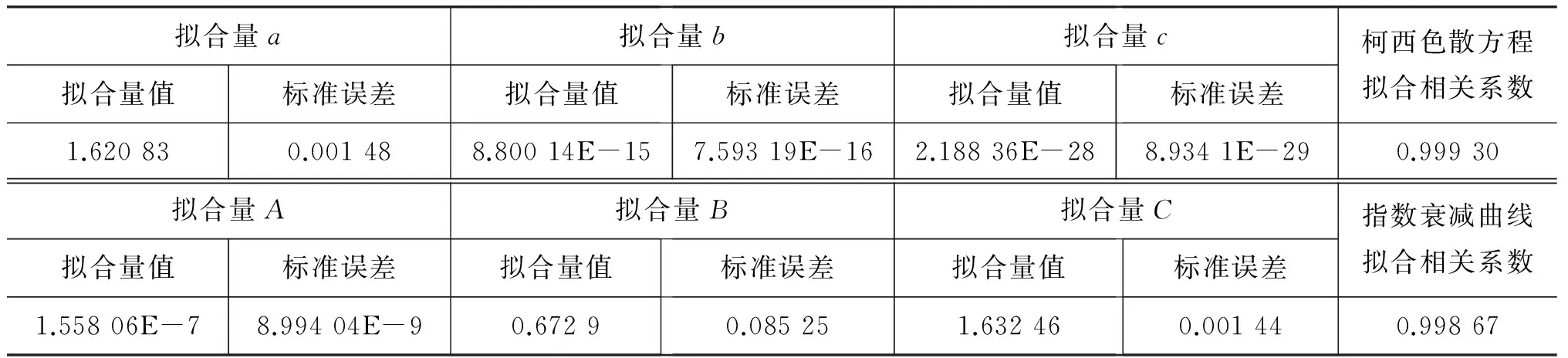
表4 最小偏向角法测得第二组折射率数据的色散方程拟合结果
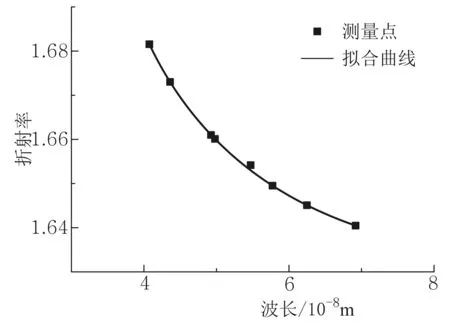
图1 最小偏向角法测得折射率(第一组最小偏向角法实验数据)的柯西色散方程最小二乘法拟合曲线
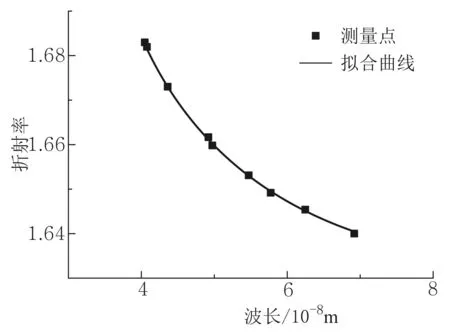
图2 最小偏向角法测得折射率(第二组最小偏向角法实验数据)的柯西色散方程最小二乘法拟合曲线
从表3及表4的结果分析得出,采用最小偏向角法测得折射率,并进行色散方程拟合,拟合的参量b及c的标准误差达到了与对应参量相差一个量级以内.这在一些色散曲线的应用实验中,可能难于满足要求,如基于法拉第磁光效应测量电子荷质比的实验中,要求获得较小不确定度的b、c拟合量[6].最小偏向角法测量得到的实验数据无论采用柯西方程还是指数衰减方程来拟合,获取的相关系数比较小,有待提高.因在实验中,最小偏向角精确位置判断的不准,引入一定的误差,从而使最小偏向角法未能满足高精度测量的要求.
2 多点测量拟合方法获取介质的色散
实验中,为了满足高精度测量要求,依据选定样品棱镜后,对于入射波长λ的光线,其偏向角满足与入射角、折射率所成的函数关系曲线关系,选择测量的有利区域,进行系列入射角、偏向角的可靠位置测量,并实现其最小二乘法的入射角、偏向角函数关系式(3)的拟合,从而获得对应入射波长的介质折射率,进而利用origin进行系列谱线折射率的色散方程式(5)的最小二乘法拟合,得到所拟合出的介质色散方程.
在不同实验环境利用多点测量方法获得二组数据,表5、表6分别对应多点测量方法的第一组、第二组实验数据.实验中,选择不同的入射波长,利用入射角与偏向角多点测量及拟合方法,获得系列谱线的折射率.
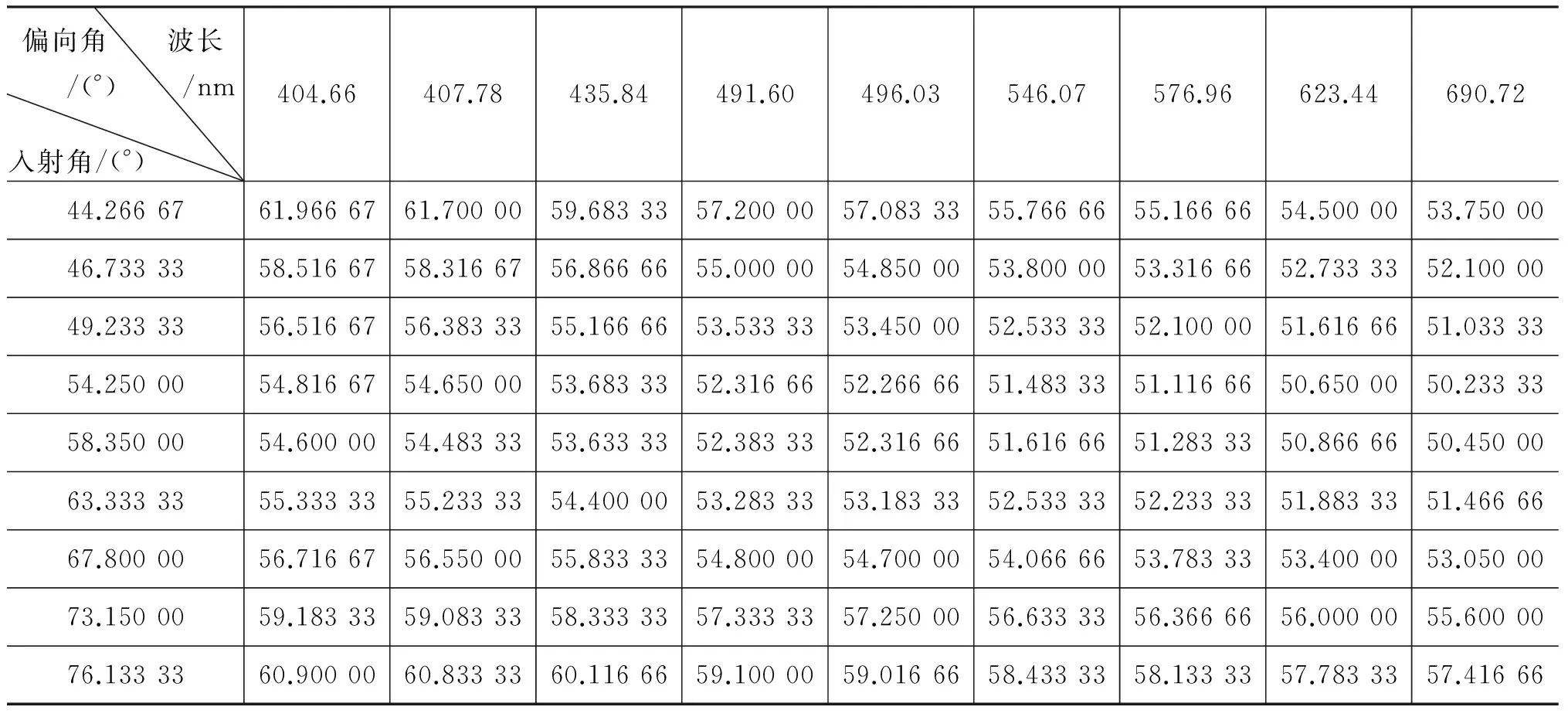
表5 实验测得不同波长入射样品棱镜,对应入射角与出射角的第一组实验结果
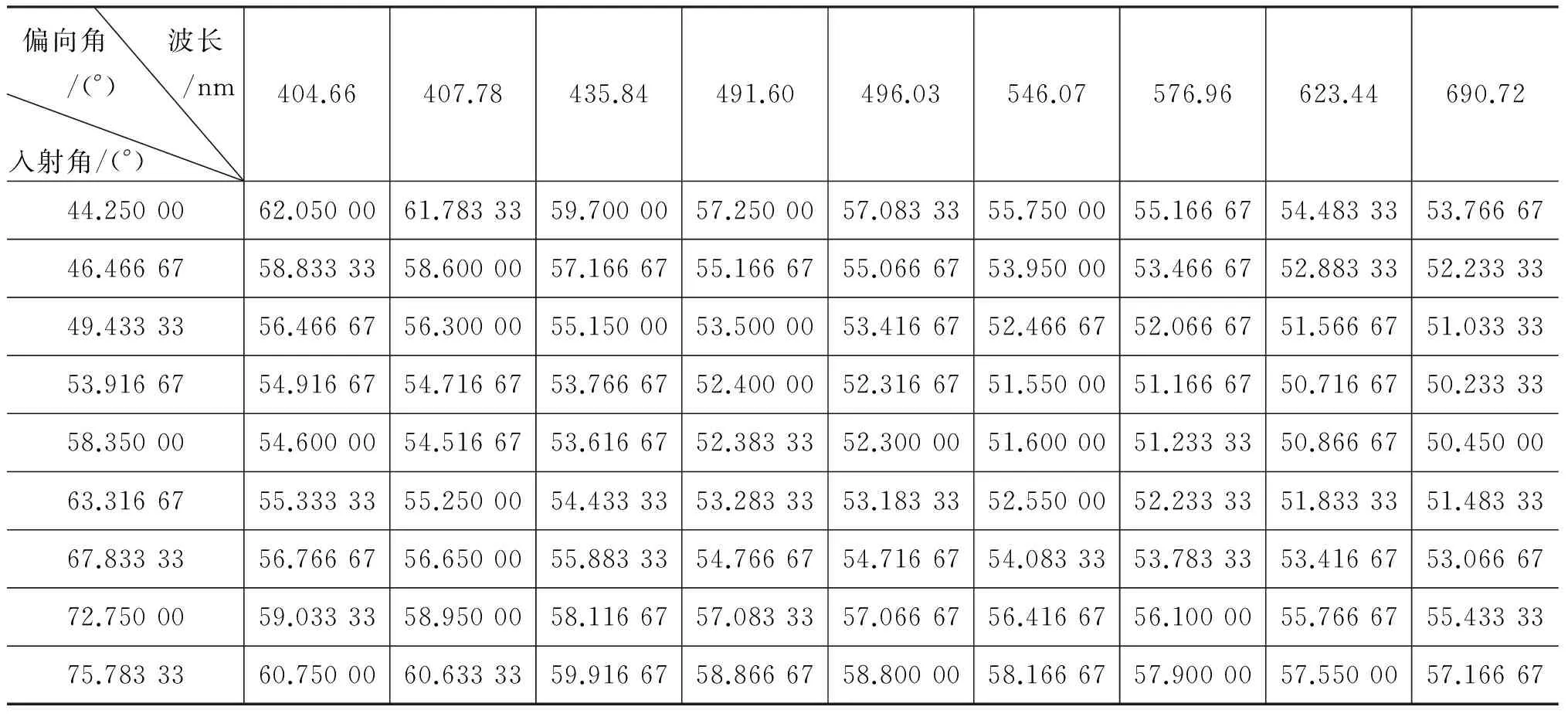
表6 实验测得不同波长入射样品棱镜,对应入射角与出射角的第二组实验结果
对表5所测数据进行入射角、偏向角及折射率的函数关系式(3)最小二乘法拟合,结果如图3所示,并得到系列谱线的折射率,如表7、表8所示.

入射波长λ/nm404.66407.78435.84491.60496.03546.07576.96623.44690.72折射率n1.682721.681601.672991.660761.659971.652691.649231.645041.64043拟合相关系数0.999890.999820.999900.999850.999950.999950.999940.999910.99995

表8 实验测得的第二组数据以不同波长入射样品棱镜,对应的折射率拟合结果
图4所示为表7中不同波长对应的折射率进行柯西色散方程最小二乘法拟合结果.
从表9、表10多点测量法进行柯西色散方程的拟合结果分析得出,多点测量法各拟合量的相对误差小于最小偏向角法拟合的结果.文献[11]中有类似的最小偏向角法直线拟合出色散特性系数的结果,系数a及b的相对误差也同样比本文的多点测量法的大,相关系数为0.999 23,也比本文多点测量法的小.在一些高精度色散测量要求的应用中,最小偏向角法未能满足要求,而多点测量法则是较为理想的一种选择.

图4 多点测量拟合法获得折射率的柯西色散方程最小二乘法拟合曲线

拟合量a拟合量b拟合量c拟合量值标准误差拟合量值标准误差拟合量值标准误差拟合曲线相关系数1.622261.37E-048.07E-157.03E-172.99E-288.27E-300.99999

表10 多点测量拟合法第二组实验获得折射率的柯西色散方程的拟合结果
3 测量结果分析及结论
对多点测量方法获得折射率进行柯西色散方程拟合的结果与最小偏向角法拟合的结果进行比较得出,多点测量拟合法可获得较小的实验相对误差.最小偏向角法的拟合相关系数无论采用柯西方程还是指数衰减方程拟合,该相关系数都比较小.采用多点测量法所拟合出参量结果的标准误差达到了与对应参量相差二个量级,拟合相关系数高达0.999 99.这些数据表明,最小偏向角法因其临界位置判断有一定的困难,造成一定误差,而多点测量拟合方法,虽测量数据量大,能避开测量不利区域,有效地提高了实验的可靠性,实现了高质量的测量,因此,多点测量法可作为一种高精度测量介质折射率及拟合色散方程的补充方法.
[1]姚启钧.光学教程[M].北京:高等教育出版社,2002:159;356-362.
[2]俞胜清,王峰,黄晓俊.重火石玻璃ZF1棱镜色散关系的测定[J]. 喀什师范学院学报,2010,30(2):44-46.
[3]周凯宁,肖宁,陈棋,等.3种测量三棱镜折射率方法的对比.[J].实验室研究与探索,2011,30(4):22-25.
[4]赵凯华.新概念物理教程:光学[M].北京:高等教育出版社,2004 :11-14;325-327.
[5]葛松华,唐亚明.测量玻璃折射率实验的讨论[J].大学物理实验,2010,23(1): 7-8.
[6]杨会静,孙立萍.法拉第效应实验中样品介质的色散与波长的关系[J].唐山师范学院学报,2005,27(2):38-39.
[7]杨小静,常缨,朱鹤年.非最小偏向角测棱镜折射率合成不确定度的探讨[J].物理实验,2013,33(6):33-34.
[8]张奕雄. Snake模型应用于塞曼效应分裂图谱处理[J].大学物理,2010,29(1):39-41.
[9]王秀峰.数据分析与科学绘图软件ORIGIN详解[M] . 北京:化学工业出版社,2008:365-387.
[10]杨之昌,王建华,马世红.测量不确定度在光学实验教学中的应用[J].物理实验,2007,27(5):31-35.
[11]王小怀,李卓凡.基于法拉第效应的电子荷质比测量及不确定度分析[J].大学物理实验,2010,23(3): 65-68.
Comparison of the multi-point measuring method and the least deviation angular method in the measurement of dispersion relation
ZHANG Yi-xiong
(Department of Physics and Electronic Engineering, Hanshan Normal University, Chaozhou, Guangdong 521041, China)
Based on the multi-point measurements, the refractive index is fitted from the data of non-least deviation angular by the nonlinear-fitting of Origin (software), to gain the dispersion relation of sample. The multiple point measuring method can be used to improve the degree of accuracy of dispersion relation of sample and achieve higher precision measurement than the least deviation angular method, by comparing multiple point measuring method and the least deviation angular method of fitting results of dispersion equation.
multi-point measuring and fitting method; least deviation angular; refractive index; nonlinear-fitting; dispersion relation
2015-01-20;
2015-11-20
广东省高等学校教育技术中心立项试验课程项目(GDHBL017)资助
张奕雄(1979—),男,广东五华人,广东潮州韩山师范学院物理与电子工程系实验师,硕士,主要研究方向:光学、近代物理.
O 482.55
A
1000- 0712(2016)04- 0033- 05

