利用傅里叶变换研究一维δ势阱原子链中的束缚态
康 举,陈建宏
(兰州城市学院 培黎工程技术学院,甘肃 兰州 730070)
利用傅里叶变换研究一维δ势阱原子链中的束缚态
康举,陈建宏
(兰州城市学院 培黎工程技术学院,甘肃 兰州730070)
利用傅里叶变换方法求解有限个δ势阱一维原子链的薛定谔方程,得到了这些原子链的能级公式.本文所用方法也为微材料能级结构的研究提供了一个有价值的理论参考.
傅里叶变换;δ势阱;一维原子链;能级
在理论上研究宏观尺寸材料的能级结构时, 通常采用无限长或半无限长周期性原子链模型[1-5].然而,近年来研究比较热门的微材料尺寸仅仅有几十到几百个nm.若继续采用上述无限长或半无限长周期性原子链的模型,理论结果显然无法与实验结果一致[6].因此,本文将这些微材料结构简化成具有有限个δ势阱的原子链, 并且利用傅里叶变换方法求解定态薛定谔方程, 最后得到了该模型相应的能级公式.
1 一维单个δ势阱中运动粒子束缚态的求解
一维δ势阱的势函数为[ 7-10]
U(x)=-γδ(x)
(1)
其中γ为表示势阱强度.
一维定态薛定谔方程为
(2)
将式(1)代入式(2)可得
(3)
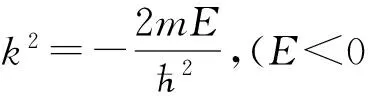
傅里叶变换式为[11]
(4)
(5)
利用式(4)对式(3)进行傅里叶变换可得
(6)
由式(6)得
(7)
利用式(5)对式(7)进行傅里叶反演变化可得
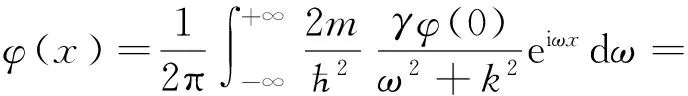
(8)
由于
(9)
由式(9),式(8)可重写为
(10)
令x=0可得
(11)
(12)
式(12)即为一维单个δ势阱中运动粒子的能级公式.
由波函数的归一化可得
(13)
由式(13)可得
(14)
由于势函数U(x)=U(-x),归一化的波函数为
(15)
为偶函数,则束缚态的本征能量有确定的偶宇称态.
2 一维两个δ势阱中运动粒子束缚态
一维两个δ势阱的势函数为
U(x)=-γ[δ(x)+δ(x-a1)]
(16)
其中γ为表示势阱强度.将式(16)代入式(2)可得
(17)
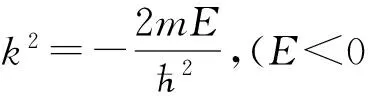
利用式(4)对式(17)进行傅里叶变换可得
(18)
由式(18)可得
(19)
利用式(5)对式(19)进行傅里叶反演变化可得
(20)
利用式(9),式(20)可写为
(21)
在式(21)中分别令x=0和x=a1,可得

(22)
(23)
联立式(22)和式(23)可得
(24)
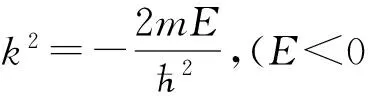
由波函数的归一化可得
(25)
由式(24)和式(25)可得
(26)
所以归一化后的波函数为
(27)
因此,可求得一维两个δ势阱中运动粒子的能级公式为
(28)
3 推广到有限多个δ势阱中运动粒子束缚态
一维n个δ势阱的势函数为
(29)
其中γ为表示势阱强度.
将式(29)代入式(2)可得
(30)
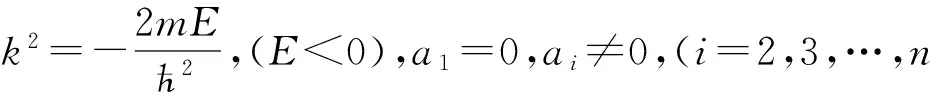
利用式(4)对式(30)进行傅里叶变换可得
(31)
由式(31)可得
(32)
利用式(5)对式(32)进行傅里叶反演变换可得
(33)
利用式(9),式(33)可写为
(34)
在式(34)中分别令x=a1,a2,…,an,则
(35)
由式(35)可得
(36)
由波函数的归一化可得
(37)
由式(36)和式(37)可得
(38)
所以归一化后的波函数为
(39)
4 结论
利用式(12)和式(15)可以确定一个周期δ势阱原子的能级、归一化的波函数和具有唯一确定的偶宇称态,其结果与文献[7-9,11]中的结果一致.利用式(36)和式(39)可以确定有限多个δ势阱原子链的能级和归一化的波函数.若将有限个δ势阱原子链简化为一个δ势阱和两个δ势阱,将其分别代入式(36)和式(39),所得结果与本文第一节和第二节中单独讨论的结果一致.以上结果表明,本文所采用的方法在理论上是合理的,可以为微材料能级结构的研究提供一个有价值的理论参考.
[1]McGill T C,Collins D A. Prospects for the future of narrow band gap materials [J]. Semicond Sci Technol,1993,8(1):S1-S5.
[2]Slater J C. Wave functions in a periodic potential[J]. Phys Rev,1937, 51(10):846-851.
[3]Herring C.A new method for calculating wave functions in crystals[J]. Phys Rev,1940, 57(12):1169-1177.
[4]LafonEarl E,Chaney Roy Cand LinChun C. Recent developments in applying and extending the method of tight binding (LCAO) to energy-band calculations [M].New York: Springer,1971:284-295.
[5]Slater J C. An augmented plane wave method for the periodic potential problem[J]. Phys Rev,1953,92(3):603-608.
[6]李正中.固体理论[M].北京:高等教育出版社, 1995:238.
[7]曾谨言.量子力学教程[M].北京:科学出版社,2007:45-47.
[8]钱伯初.量子力学[M].北京:高等教育出版社, 2008:49-51.
[9]钱伯初.曾谨言.量子力学习题精选与剖析[M].3版.北京:科学出版社, 2009: 29-36.
[10]黄明举.有限长周期δ势原子链能级的确定[J].河南大学学报,1996, 26(3):25-28.
[11]梁昆淼,等.数学物理方法[M].4版.北京:高等教育出版社,2010:56-78.
Investigations on the bound states of delta potential wells in one-dimensional atomic chain using Fourier transform
KANG Ju, CHEN Jian-hong
(School of Bailie Engineering and Technology, Lanzhou City University, Lanzhou, Gansu 730070, China)
Fourier-transform method is used for solving Schrödinger equation with delta potential wells in one-dimensional atomic chain. The formula describing the energy levels of the atomic chain is obtained. The method used in this paper is a valuable theoretical reference for studying the energy-level structure of micro-material.
Fourier transform; delta potential well; one-dimensional atomic chain; energy level
2015-05-16;
2015-11-20
国家自然科学基金(11164012)、兰州市科技计划项目(2012-2-105)、兰州城市学院本科教育教学研究项目(2014-jy-01)资助
康举(1992—),男,甘肃陇南人,兰州城市学院培黎工程技术学院物理系2012级本科生.
陈建宏,E-mail: chenyuwen1982@163.com.
大学生园地
O 413.1
A
1000- 0712(2016)04- 0049- 03

