近零折射率超材料波导加载系统中数理方程的求解及COMSOL仿真

曹斌照，费宏明，杨毅彪，薛萍萍

(太原理工大学 物理与光电工程学院，山西 太原　030024)



近零折射率超材料波导加载系统中数理方程的求解及COMSOL仿真

曹斌照，费宏明，杨毅彪，薛萍萍

(太原理工大学 物理与光电工程学院，山西 太原030024)

近零折射率超材料波导中加载介质缺陷的电磁波传输特性的分析归结为“数学物理方法”中亥姆霍兹方程非齐次边值问题的求解，可采用多种求解偏微分方程的方法进行分析. 本文用分离变量法对这一问题的两个典型实例进行了解析求解，并通过基于有限元法的多物理场耦合仿真软件COMSOL Multiphysics进一步对照，从而验证了理论分析的正确性. 对更一般的问题采用COMSOL进行了数值计算和仿真，其适用性更为普遍.

近零折射率超材料；亥姆霍兹方程边值问题；分离变量法；数值法

近年来，人工电磁材料(又称为超电磁材料，Metamaterials)受到了国内外学者的广泛研究[1].作为人工电磁材料之一——近零折射率超材料(Nearly Zero-Index Materials, NZIM)，因其具有诸多超常特性也倍受关注. 对NZIM的研究表现在诸多应用领域，例如利用其实现电磁场超耦合效应、辐射场整形、高性能辐射、光子隧穿效应、电磁波的吸收、波导型传感器、光子颤振效应等. 另一方面，利用NZIM来调控电磁波在波导中的传播也受到了不少学者的研究. 例如利用NZIM实现电磁波的完美弯曲和透射、在NZIM中嵌入介质柱实现波的全透射和全反射等[2,3].

根据宏观电磁理论，时谐电磁波在任何媒质中的传播特性均可归结为亥姆霍兹方程的定解问题[4]. 按照“数学物理方法”理论，这类偏微分方程有多种求解方法[5-7]. 对于一些具有规则边界的情形，分离变量法是一种有效的分析方法；而对于边界形状比较复杂的不规则情形，一般只能采用数值法. 对于前者，一般教科书中对亥姆霍兹方程的边值问题，只针对齐次边界条件问题做了一些简单介绍，即使专业课程如“电动力学”、“电磁理论”等也未涉及非齐次边界条件下的定解问题[4,8]. 这是因为多数情况下亥姆霍兹方程的应用背景总是与本征值问题相联系，往往满足齐次边值条件. 如电磁工程问题中波导、谐振腔等.

据笔者不完全了解，鲜有专门讨论亥姆霍兹方程在非齐次边界条件下定解问题的教学内容. 而个别文献虽然有涉及这方面的内容，但要么是结果不完善[2]，或者没有具体分析过程[3].

故此，本文针对NZIM波导中加载介质缺陷的电磁波传输问题，并结合我们在“数学物理方法”的本科教学，提炼出了亥姆霍兹方程非齐次边值问题的求解方法. 对矩形、圆柱形两类规则形状的边界，在直角坐标系和圆柱坐标系中分别用分离变量法进行了求解，并通过基于有限元法的多物理场耦合仿真软件COMSOL进行了对照；同时对其物理意义进行了深入分析、讨论. 对于不规则边界的同类问题，用COMSOL进行了数值求解和仿真.

1　模型及理论推导

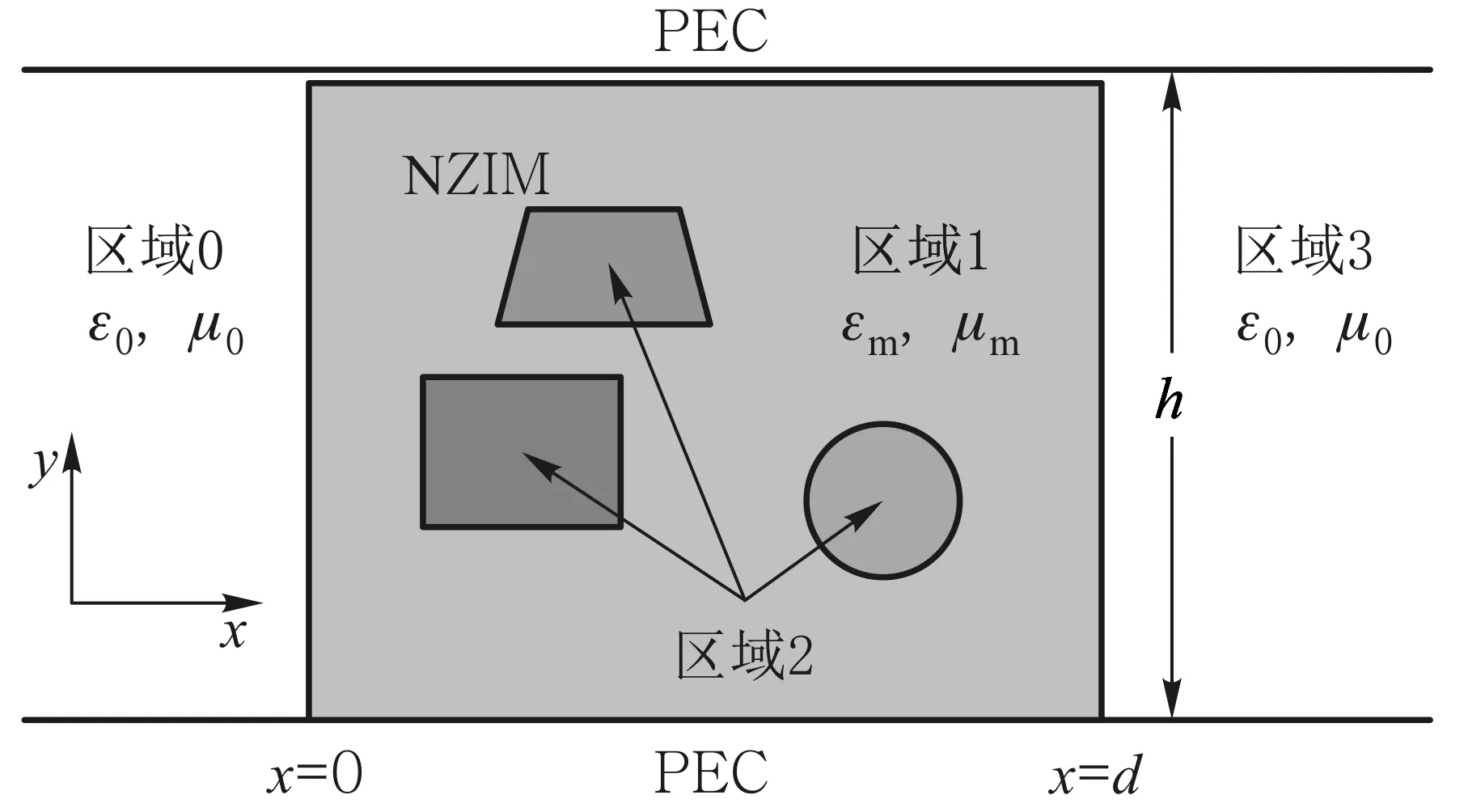
图1　二维近零超材料波导加载系统

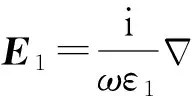
(1)

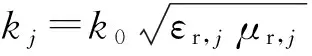
1.1矩形截面介质柱情形

若加载缺陷为一矩形截面介质柱，柱内电磁场的定解问题可归结为

(2)

应用叠加原理，将边界条件进行齐次化，令φ=φ′+φ0，则原问题可化为

(3)

这是一个非齐次泛定方程具有齐次边值条件的定解问题. 用分离变量法(傅里叶级数法)，设

(4)

代入式(3)中的泛定方程，得

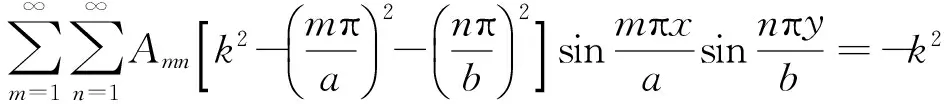
(5)

利用本征函数的正交性，得

(6)

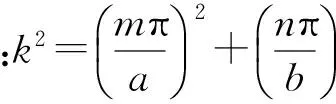
(7)

若k=0，上式便简化为φ(x,y)=φ0.事实上，这种情况下，定解问题式(2)可退化为

(8)

此为普拉斯方程的定解问题，其解显然为φ=φ0.

1.2圆柱形介质柱情形

若加载缺陷为一圆柱形介质柱，柱内电磁场的定解问题可归结为

(9)

类似地，令φ=φ′+φ0，原问题可化为

(10)

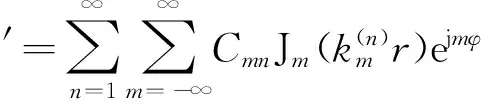
(11)

利用本征函数的正交性，得

(12)

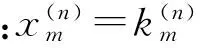
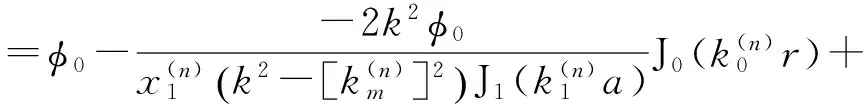
(13)

2　仿真及分析

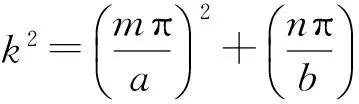
图2　　　　波导内加载矩形介质柱磁场发生的全反射现象

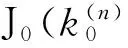
图3　　　　波导内加载矩形和圆形介质柱磁场发生的全透射现象

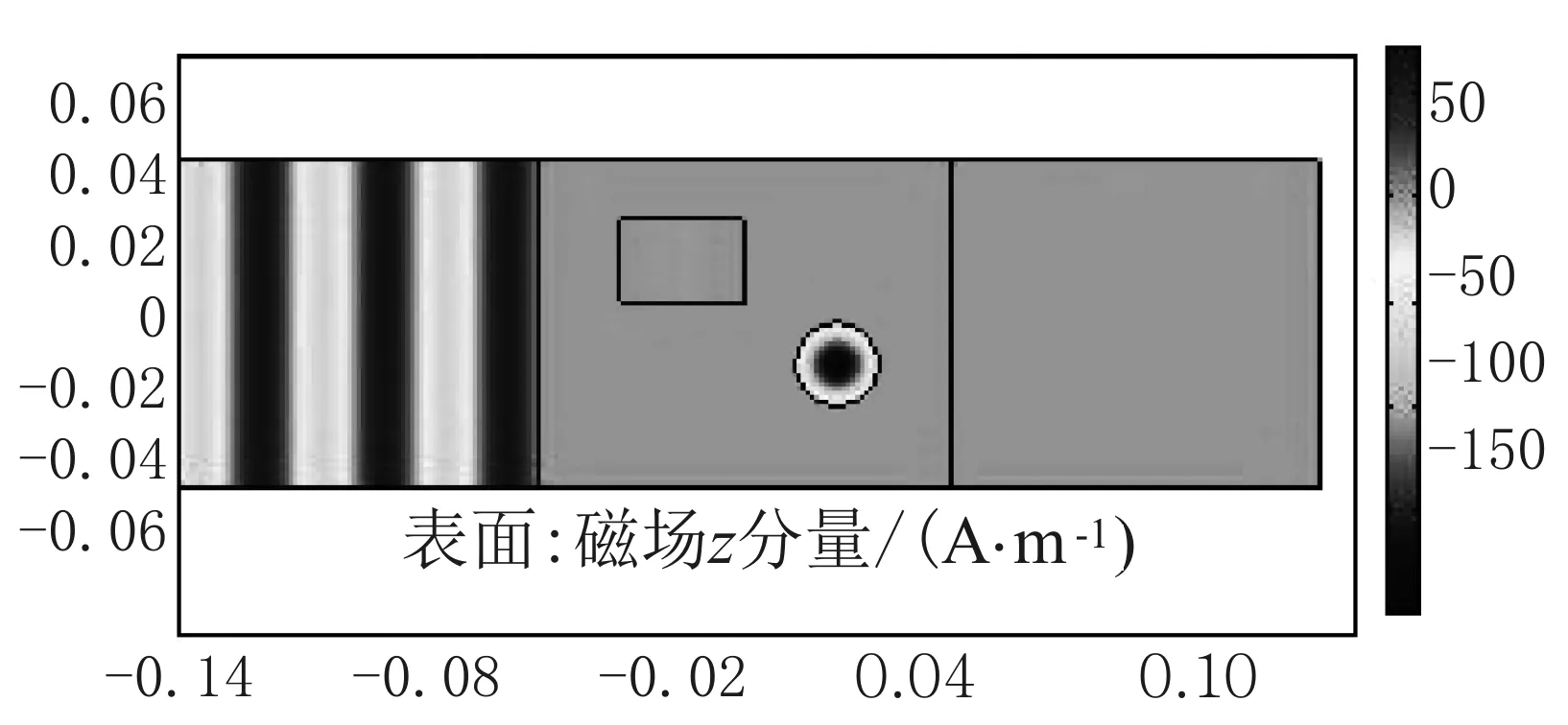
图4　　　　仅圆柱形介质柱内发生谐振，电磁波发生全反射

对于任意截面的介质柱，一般得不到解析解，但我们可以用COMSOL软件计算谐振频率及传输系数. 以一底角为45°的直角梯形为例，选取上底a=0.01 m、下底b=0.02 m、高h=0.01 m，进行数值计算，反射系数随梯形介质柱的曲线如图5所示. 当εr2≈3.5和6.7时发生全反射；当εr2≈6.5和7.2时发生全透射.用COMSOL仿真结果如图6所示.两者结论完全吻合.

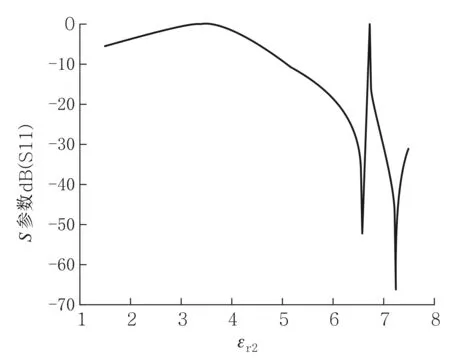
图5　梯形介质柱内反射系数随介质柱介电常数的变化关系

图6　梯形介质柱内发生谐振，电磁波发生全反射或全透射现象

3　总结

本文对于近零折射率超材料波导中加载规则介质缺陷的电磁波传输特性问题用分离变量法进行了解析求解，对不规则介质缺陷问题采用多物理场耦合仿真软件COMSOL Multiphysics进行了数值计算.在具体应用实例中，坐标系原点的选择对分析结果没有影响.采用COMSOL仿真计算适用于任何情况，因此更具有普遍性.

[1]Engheta N,Ziolkowski R W Eds. Metamaterials:Physics and Engineering Explorations[J]. John Wiley & Sons, 2006,37:180-193.

[2]Nguyen V C, Chen L, Halterman K. Total transmission and total reflection by zero index metamaterials with defects[J]. Physical review letters, 2010, 105(23): 233908.1-4.

[3]Ying Wu, Jichun Li. Total reflection and cloaking by zero index metamaterials loaded with rectangular dielectric defects[J]. Applied Physics Letters, 2013, 102(18): 18310.1-4.

[4]张克潜,李德杰.微波与光电子中的电磁理论[M].2版.北京: 电子工业出版社，2001: 173-223.

[5]梁昆淼.数学物理方法[M].4版.北京: 高等教育出版社，2010:162-179;265-280.

[6]杨孔庆. 数学物理方法[M].北京: 高等教育出版社，2012: 180-202; 255-292.

[7]四川大学数学学院高等数学、微分方程教研室. 高等数学(第4册) [M].3版. 北京: 高等教育出版社，2010.

[8]郭硕鸿.电动力学[M].3版.北京: 高等教育出版社，2008: 128-135.

Analytical solution of equation of mathematical physics in the waveguide system loaded with nearly-zero-index-metamaterials and simulation by using COMSOL

CAO Bin-zhao, FEI Hong-ming, YANG Yi-biao, XUE Ping-ping

(College of Physics and Optoelectronics, Taiyuan University of Technology, Taiyuan, Shanxi 030024, China)

The transmission characteristics of electromagnetic wave in the waveguide system, filled with nearly-zero-index-metamaterials and loaded with dielectric defects, belongs to the problem of Helmholtz equation with non-homogeneous boundary value in the source of the method of mathematics. It can be solved by a variety of methods for solving partial differential equations. In this paper, the separation variables method is used for solving two typical examples. Furthermore, the software named COMSOL multi-physics, which is based on the finite element method, is used for simulation, and the correctness of theoretical analysis is certified. For more general problems, numerical calculation and simulation by COMSOL are more commonly applied.

nearly-zero-index-metamaterials; problem of Helmholtz equation with boundary values; separation variables method; numerical method

2015-03-04；

2015-11-16

2014年度太原理工大学“本科教育教学改革项目”、2014年度高等学校“数学物理方法”课程专业教学指导委员会研究项目[JZW-14-SL-12]资助.

曹斌照(1967—)，男，山西临县人，太原理工大学物理与光电工程学院副教授，博士，主要从事电磁理论、数学物理方法的教学与研究.

O 411.1

A

1000- 0712(2016)04- 0015- 04