量子相变与量子纠缠

刘光华，邓小燕

(1. 天津工业大学 物理系，天津　300387;2. 天津工业大学 研究生院，天津　300387)



量子相变与量子纠缠

刘光华1，邓小燕2

(1. 天津工业大学 物理系，天津300387;2. 天津工业大学 研究生院，天津300387)

作为量子体系一种内在的非局域性关联，量子纠缠已经成为一个可利用的重要资源并广泛应用于许多领域. 强关联体系中的量子相变，作为凝聚态理论中的一个重要现象，也一直是人们研究的热点. 本文介绍了量子纠缠的定义，纠缠的判据，以及纠缠的度量. 接着，通过一个具体模型对如何利用量子纠缠描述量子相变进行讨论和分析. 研究发现，在强关联体系量子相变中量子纠缠扮演着非常重要的角色.

非局域关联；量子纠缠；量子相变

量子纠缠是为了解释量子力学中许多违反直觉的非局域性物理过程而提出的一个基本概念. 也就是说，量子纠缠是量子体系中存在的一种没有经典对应的非局域性关联. 现在，量子纠缠已经作为一种重要的资源而应用于量子密码术、高密度编码、量子态的传输以及量子计算等许多领域[1-4]. 量子纠缠的研究已经发展成为量子信息理论中非常重要的课题之一. 另外，强关联体系中的量子相变，作为凝聚态理论中的一个重要现象，也一直是人们研究的热点. 在临界点附近，强关联系统的量子涨落变得非常剧烈，因而导致体系关联长度的发散. 鉴于量子纠缠和量子相变均与非局域性关联关系密切，凝聚态物理中常利用量子纠缠的具体行为来描述量子体系的量子相变. 本文首先对量子纠缠和量子相变等物理概念进行介绍，接着对海森伯-易辛交替自旋模型的量子相变进行具体描述，让读者对量子纠缠和量子相变之间的关系有个较为深刻的理解.

1　量子纠缠

量子理论深刻地改变了人类社会，推动了核能、激光、半导体等高科技的高速发展. 但是，量子理论曾经引起的困惑至今仍然困扰着人们，自然界是否确实按照量子理论的规律运行？为此，量子力学出现了两大阵营：以爱因斯坦为代表的一方始终认定量子力学不是完备的理论，“上帝是不会玩骰子的”；而以哥本哈根学派领袖玻尔为代表的另一方则坚信量子理论的正确性. 在这场量子力学近百年的学术争论中，影响最大的两件事就是同在1935年由薛定谔提出的“薛定谔猫”佯谬[5]和由爱因斯坦等人提出的EPR佯谬[6]. 这些争论的本质在于，真实世界是遵从爱因斯坦的局域实在论，还是玻尔的非局域性理论. 长期以来，这个争论一直停留在哲学层面上，难以判断“孰是孰非”，直到贝尔(Bell)基于爱因斯坦的隐参数理论而推导出著名的贝尔不等式，人们才有可能在实验上依据贝尔不等式寻找判定这场争论的依据. 后来，有人在实验上证实了贝尔不等式可以违背，即爱因斯坦的局域实在论在微观世界不是真理，支持了玻尔的看法. 之后，随着量子光学的发展，有更多的实验支持了这个结论，即宏观世界遵守贝尔不等式，而微观世界能够违背贝尔不等式. 可见，很多实验结果的确和量子力学的结论是一致的[7]，虽然还是有人认为在实验的设想上还存在一些漏洞[8]. 现在人们知道，“EPR佯谬”中揭示的量子关联效应(非局域性)常被称为EPR效应，而且非局域性是量子力学的基本性质.

事实上，按照量子力学理论，EPR粒子对是处于所谓纠缠态的一对粒子，这个量子状态最大地违背贝尔不等式，它有着奇特的性质：人们无法单独地确定某个粒子处在什么量子态上，这个态能给出的唯一信息就是它的整体特性：“两个粒子之间的相互关联”. 现在实验上已成功地制备出这类具有纠缠性的量子态.

1.1纠缠态

量子力学发展史上两个著名的佯谬都涉及纠缠态的概念，下面对这个重要的物理概念进行一些定量的讨论. 所谓复合体系就是由两个或两个以上子系统组成的体系，而最简单的复合体系是由两个量子位(每个量子位具有两个自由度:|0〉或|1〉)组成的一个体系. 每个量子位就是一个子系统，把它们分别叫作A和B. 在量子通信和纠缠理论中这两个子系统分别隶属于两个被分离开来的观察者:Alice和 Bob. 两个子系统的任何状态都可以分别表示成:

|Ψ〉A=α|0〉A+β|1〉A，|Ψ〉B=γ|0〉B+δ|1〉B

(1)

其中α2+β2=1，γ2+δ2=1. 这样一来，这两个子系统组成的复合体系状态则可以用这两个子系统的状态的直积来表示:

|Ψ〉直积=|Ψ〉A⊗|Ψ〉B

(2)这样的一个状态叫直积态，但是直积态并不是唯一物理上可实现的状态. 如果让A和B这两部分之间相互作用，状态就应该是这些直积态的叠加. 所以，一般意义上的复合体系状态可以写成叠加态的形式:

(3)

如果一个复合态仅包括两个部分，这样的态就叫二分(bipartite)态，而包括两个以上部分组成的复合态叫作多分(multipartite)态. 两个量子位组成的复合态，可以写成4个纠缠态，分别是一个单重态

(4)

和3个三重态

(5)

其中|ij〉是|i〉⊗|j〉的缩写. 这4个纠缠态扮演着重要角色，也就是众所周知的Bell态或EPR对. 它们一起组成了两个量子位态空间的一组正交归一的完备基组，叫Bell基组. Bell态是最大纠缠态，可以通过对其中任何一个子系统进行幺正变换，从而使4个基之间可以实现相互转换. 值得注意的是，如果对Bell态中的其中一个qubit的状态进行测量(对于z方向有两个本征值±1)，马上就可以知道另一个qubit的状态. 比如，在单重的Bell态中对A量子位的本征态进行测量，结果可能是|0〉或者|1〉，概率分别是1/2. 当A的本征态一旦确定为|0〉(或|1〉)，B的本征态就一定是|1〉(或|0〉). 爱因斯坦曾把它称为幽灵式的超距作用.

1.2Schmidt分解

Schmidt分解是研究处理由两个部分(bipartite)组成的纯态中纠缠的一个非常有用的工具. 它能把基组分解成双正交的基组，从而对于一个直积基组能给出最少的基底. 对于一个给定的bipartite纯态|φ〉，都可以用由这两个子系统相互正交的基组的直积进行展开：

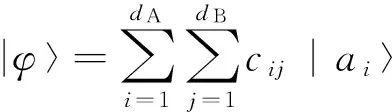
(6)

其中c是一个dA×dB的系数矩阵，它通过奇异值分解可以写成

c=UDV

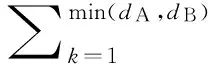
(7)

根据上式，构建新的基底：

(8)

并且重新定义λk=dkk，这样就可以得到最后的形式：

(9)

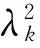
1.3纠缠的判据

对于一个给定的量子态，一个首先感兴趣并想问的问题是:它是否是纠缠的?或者说 它是否是可分离的? 可分离的态是一个没有纠缠的态，它的每一个子系统都可以通过自身来描述. 对于纯态来说，只有那些可以写成直积(如式(2)所示)形式的态才是可分离的态. 如果这个态不是直积态，那它就是一个纠缠态. 在实际的操作中，人们只有找到这组恰当的基组，才能把它写成如式(2)那样的直积形式. 这样做有点困难，所以需要另一个更简单的判断方法，比如前面部分介绍的Schmidt分解. 就像前面提到的那样，Schmidt系数就是约化密度矩阵本征值的平方根. 因此，Schmidt秩也就是约化密度矩阵的非零本征值. 通过Schmidt秩还可以获得的信息是体系中有多少自由度是纠缠的. 对于一个可以写成式(2)那样的直积态，Schmidt秩是等于1的，此时就说体系是非纠缠的. 对于一个纯态，这是一个判断体系是否可分离或是否纠缠的必要充分条件. 因此，通过Schmidt秩可以把由两部分组成的纯态划分为可分离和纠缠态.

1.4纠缠的度量

理论上，有两条途径来量化纠缠. 一是操作性测量(operational measures)，它是基于如何使某一任务能较好的执行基础上的，通常要和Bell态相比较. 二是抽象测量(abstract measures)，即从一些纠缠测量应该满足的一些自然公理出发，然后再寻找满足这些公理的函数. 自从关于一些如何度量纠缠的文章[9-12]发表以来，这一课题已经发展成了一个新的研究领域. 然而，如何定量地描述混合系综的纠缠，仍然是一个没有完全解决的难题.

在纠缠的度量中，由约化密度矩阵定义的冯·诺依曼熵是一个非常重要的物理量. 两个子系统中任何一个的冯·诺依曼熵(两者的熵是相等的)都能很好地用来测量纠缠. 正是由于这个原因，约化的冯·诺依曼熵又常被叫作纠缠熵ES. 纠缠熵是Bennett等人在文献[11]中第一次引入用来测量纠缠的. 对于一个由A和B两部分组成的二分量子体系，可以用约化密度矩阵来描述子体系A或者B. 约化密度矩阵ρA和ρB分别定义为

(10)

或者

(11)

从约化密度矩阵ρA或者ρB出发，纠缠熵ES可以定义为

ES(ψ)=-Tr(ρAlnρA)=-Tr(ρBlog2ρB)

(12)

很容易看出，对于两个约化密度矩阵来说，纠缠熵ES都是相等的. 我们看到纠缠熵ES具有如下一些重要性质: 1) 对于直积态，纠缠熵ES等于0； 2) 当约化密度矩阵完全混合(即子体系没有独立的自由度)时，纠缠熵取最大值； 3) 而且，在局域的幺正变换操作下，纠缠熵ES保持不变，这是纠缠的测量中的一个重要的特性.

另外，人们早就认识到矩阵乘积态(MPS)可以用来描述一维强关联体系的量子基态. 大家熟悉的一个典型例子就是严格可解的AKLT模型[13]，该模型的基态恰好是一个维数为2的矩阵乘积态. 有趣的是MPS还可以用来研究一些费米子模型[14]. 近年来的研究表明，无论是数值重整化群还是密度矩阵重整化群，基态波函数都具有MPS 态的形式[15,16]. 下面，我们将采用基于矩阵乘积态框架下的无限时间演化块消减(iTEBD)算法[17]研究具体量子体系的量子相变问题. 矩阵乘积态框架下，一维的两周期量子体系基态通常可以表示成：

(13)

其中mi表示局域物理指标，Γa(Γb)表示奇(偶)格点上的三阶张量.Λa(Λb)代表奇(偶)键上的对角矩阵. 当矩阵乘积态具有正则化形式时，人们可以砍断任意键进行Schmidt分解:

(14)

(15)

对于两周期的矩阵乘积态，就存在两个二分纠缠度量(奇数键S2i-1,2i和偶数键S2i,2i+1).

2　量子相变

量子相变是强关联体系中的一个重要的物理现象. 所谓量子相变，就是强关联体系在绝对零温条件下，由于体系耦合参数的改变而导致的体系在两个性质完全不同的相之间的改变[18]. 对于一个量子体系，如果仅改变其中某一个参量g的话，体系的哈密顿量就应该是这个参量g的函数H(g). 当参量g改变时，体系的基态可能会从一个有序态转变到另外一个有序态或者无序态，而转变点gC则称为相变点. 在这一相变点上，经常伴随着一些关联长度的发散，这个转变点又叫作量子临界点. 由于体系处于绝对零度， 没有热力学涨落，所以说量子相变纯粹是由量子涨落导致的. 一些为大家熟悉的例子有，在横向磁场中的Ising型自旋体系中发生的顺磁和铁磁相的转变；高温超导体系中随空穴掺杂浓度的增大从反铁磁有序态到超导态的转变，以及液氦中的超流绝缘体转变.

3　量子纠缠与量子相变

量子纠缠这个本来纯粹是从量子信息理论角度发展起来的物理概念，应该在量子多体物理的研究中同样扮演着非常重要的角色[19,20]. 特别是，作为量子态内在的一种特性，它和量子关联有着密切的关系. 而我们知道，量子相变同样与量子关联关系非常密切. 因而， 可以预计，在量子相变点处的量子纠缠可能会发生根本性的变化. 所以，人们自然地期望能通过对量子纠缠的研究来探讨量子相变问题.

为此，我们以海森伯-易辛交替自旋链为例对量子相变进行一些讨论. 一维的海森伯-易辛交替自旋1/2链可通过以下哈密顿量

(16)

来描述. 其中，JH和JI分别代表奇数键上的海森伯和偶数键上的易辛自旋交换作用. 为了方便，JH取为能量的单位，JI是可以变化的参量.N是自旋链格点的总数量. 当JI趋于正无穷时，体系将变成反铁磁态. 而当JI趋于负无穷时，体系基态将形成反铁磁条纹相. 当JI等于零时，基态是一个理想的无序二聚化态. 这就意味着，随着JI从负无穷变化到正无穷，体系将至少要发生两次量子相变. 体系首先从反铁磁条纹相变为无序的二聚化相，接着进入反铁磁相. 首先我们计算体系的磁化强度，磁化强度的定义为

(17)

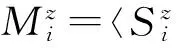
(18)

以及Néel序参量

(19)

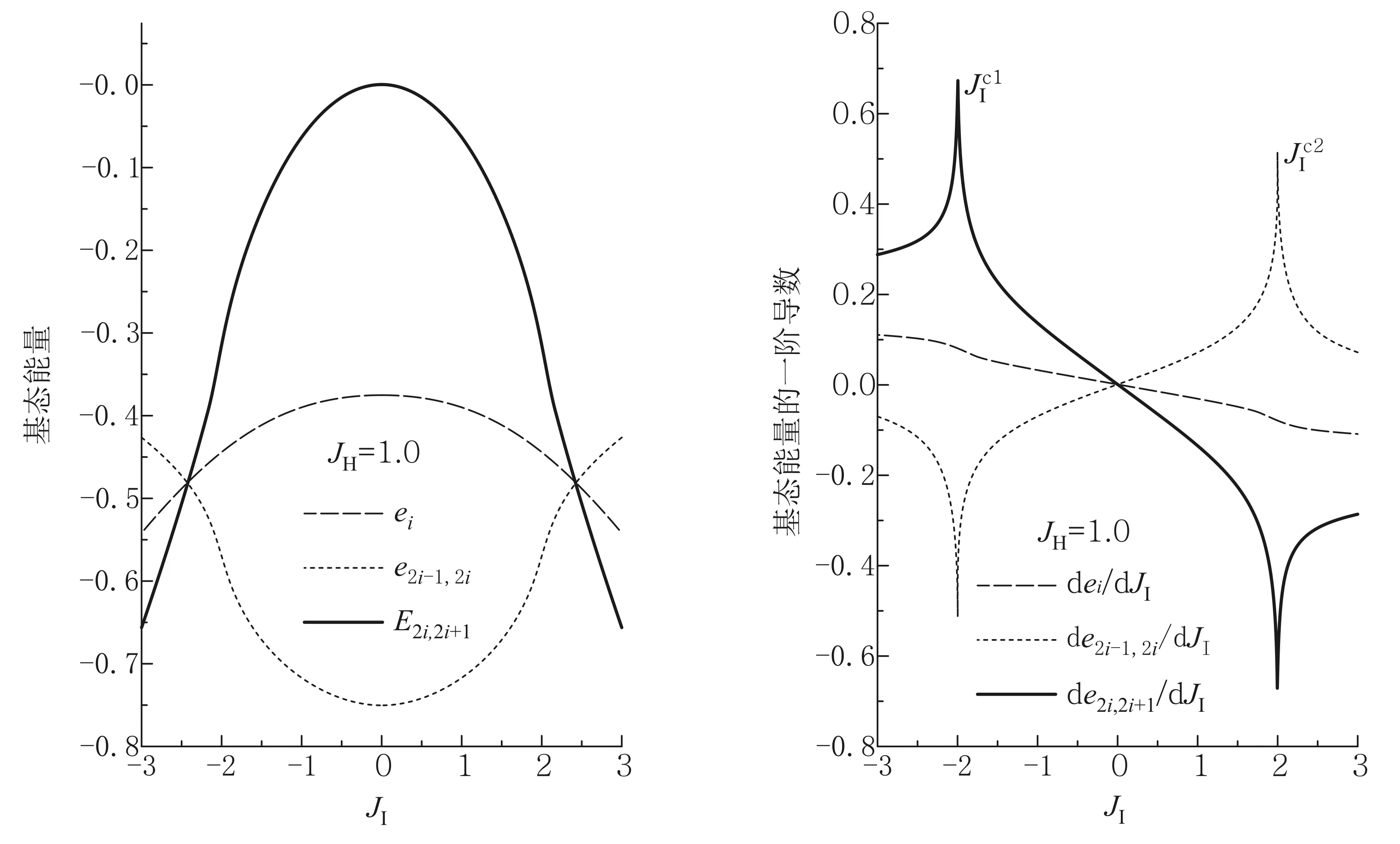
这些序参量的计算结果如图1所示. 通过图1，我们发现在整个参量区间，体系的磁化强度始终等于零. 在JI<-2区间，我们观测到了非零的反铁磁条纹序参量，而在其他两个相中反铁磁条纹序参量都等于零.JI<-2区间非零的反铁磁条纹序参量证实了反铁磁条纹相的存在. 另外，当JI>2时，Néel序参量不等于零，表明这个区间基态属于反铁磁相. 在-2

图1　磁化强度，反铁磁条纹序参量以及Néel序参量

图2　奇数键和偶数键的二分纠缠(bipartite entanglement)

为了描述JI=±2的两个量子相变，我们计算了体系随着JI变化时的二分纠缠(如图2所示). 通过图2，我们清楚地看到，二分纠缠在两个相变点(JI=±2)表现出了奇异行为. 根据以前的研究[21]，这两个奇异点代表着两个二级量子相变. 为了进一步验证这些结论，我们还计算了体系的基态能量，包括格点能量，奇数和偶数键的能量(如图3(a)所示). 研究发现，所有基态能量(包括格点能量(ei)，奇数键能量(e2i-1,2i)和偶数键能量和(e2i,2i+1))随着JI的变化表现出连续的行为. 接着,我们还计算了它们的一阶导数. 从图3(b)可见，格点能量的一阶导数仍然表现出连续行为，而键能量的一阶导数在两个相变点均现出了奇异行为. 键能量的一阶导数的奇异行为意味着这些相变属于二级量子相变的范畴[21].

格点能量(ei)和键能量(e2i-1,2i 和e2i,2i+1)　 格点能量和键能量的一阶导数图3

4　总结

一般而言，为了描述量子相，直截了当的方法是计算其具体的局域参量. 因此，序参量是依赖于具体的量子相的，不同的量子相具有不同的序参量. 特别是对于一些不能用局域序参量来描述的拓扑相变，序参量更显得无能为力. 本文利用量子纠缠的奇异行为描述了海森伯-易辛自旋1/2链的量子相变. 研究表明，量子纠缠是一种非常有效的描述量子相变的方法，而且它并不依赖于具体模型. 然而，目前仍然还有很多问题需要进一步去解决，如何有效度量量子体系的量子纠缠一直是一个难题，还需要我们不断去探索. 而且，是否还有更好的量子纠缠的度量方法仍然需要在研究的过程中不断去寻找；要想通过量子纠缠来研究量子相变，当然就需要找到这两者之间的普适联系. 因此，人们要通过对一系列量子模型进行系统研究，从中获得量子相变与量子纠缠行为的普适关系.

[1]Ekert A K. Quntum cryptography based on Bell’s theorem[J]. Phys Rev Lett, 1991, 67:661-663.

[2]Bennett C H, Wiesner S J. Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states[J]. Phys Rev Lett, 1992, 69: 2881-2884.

[3]Bennett C H, Brassard G, Crèpeau C, et al. Teleporting an unknowm quantum state via dual classical and Einstein-Podolsky-Rosen channels [J]. Phys Rev Lett, 1993, 70:1895-1899.

[4]Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM J Comput, 1997, 26:1484-1509.

[5]Schödinger E. Die gegenwärtige Situation in der Quantenmechanik[J]. Naturwissenschaften, 1935, 23:807-812.

[6]Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? [J]. Phys Rev, 1935, 47:777-780.

[7]Aspect A, Dalibard J, Roger G. Experimental test of Bell’s inequalities using time-varying analyzers[J]. Phys Rev Lett, 1982, 49:1804-1807.

[8]Santos E. Optical tests of Bell’s inequalities not resting upon the absurd fair sampling assumption[J]. Phys Lett A, 2014, 27:33-37.

[9]Schlientz J, Mahler G. Description of entanglement[J]. Phys Rev A, 1995, 52:4396-4404.

[10]Bennett C H, Brassard G, Popescu S, et al. Purification of noisy entanglement and faithful teleportation via noisy channels[J]. Phys Rev Lett., 1996, 76:722-725.

[11]Bennett C H, Bernstein H, Popescu S, et al. Concentrating partial entanglement by local operations[J]. Phys Rev A, 1996, 53:2046-2052.

[12]Bennett C H, Divincenzo D, Somolin J, et al. Mixed-state entanglement and quantum error correction[J]. Phys Rev A, 1996, 54:3824-3851.

[13]Affleck I, Kennedy T, Lieb E H, et al. Rigorous results on valence-bond ground states in antiferromagnets[J]. Phys Rev Lett，1987, 59:799.

[14]Su G. Exact ground states of one-dimensional quantum systems: matrix product approach[J]. Phys Lett A , 1996, 213:93-101.

[15]Ostlund S, Rommer S. Thermodynamic limit of density matrix renormalization[J]. Phys Rev Lett, 1995, 75: 3537.

[16]Verstraete F, Weichselbaum A, Schollwock U, et al. Variational matrix-product-state approach to quantum impurity models[J].Phys Rev B, 2009, 80:165117; Saberi H, Weichselbaum A,Delft von J. Matrix-product-state comparison of the numerical renormalization group and the variational formulation of the density-matrix renormalization group[J].Phys Rev B, 2008, 78:035124.

[17]Vidal G. Classical simulation of infinite-size quantum lattice systems in one spatial dimension[J].Phys Rev Lett, 2007, 98:070201; Orus R, Vidal G. Infinite time-evolving block decimation algorithm beyond unitary evolution[J].Phys Rev B, 2008, 78:155117.

[18]Sachdev S. Quantum phase transitions[M].Cambridge:Cambridge University Press,2000.

[19]Ghosh S, Rosenbaum T F, Aeppli G, et al. Entangled quantum state of magnetic dipoles[J]. Nature, 2003, 425:48.

[20]Guang-Hua Liu, Hai-Long Wang, Guang-Shan Tian. Existence of dimerized phases in frustrated spin ladder models[J]. Phys Rev B, 2008, 77:214418.

[21]Guang-Hua Liu, Wei Li, Wen-Long You, et al. Matrix product state and quantum phase transitions in the one-dimensional extended quantum compass model [J]. Phys Rev B, 2012, 85:184422.

Quantum phase transitions and quantum entanglement

LIU Guang-hua1, DENG Xiao-yan2

(1. Department of Physics, Tianjin Polytechnic University, Tianjin 300387, China;2．Graduate School, Tianjin Polytechnic University, Tianjin 300387, China)

Quantum entanglement, as an inherent nonlocal correlation, has become one of the important available sources, and was widely applied in many fields. The quantum phase transition in strongly correlated systems, as an important phenomenon, is still a remarkable focus in condensed matter physics. In the present paper, the conception, the criteria, and the measurement of entanglement are introduced and discussed. Then, the quantum phase transitions in a representative model are investigated, and how to describe the quantum phase transitions by the quantum entanglement is also discussed. It is found that the quantum entanglement plays a key role in quantum phase transitions.

nonlocal correlation; quantum entanglement; quantum phase transitions

2015-04-27；

2015-10-15

天津工业大学校级教学改革项目(2013-2-33)资助

刘光华( 1976—) , 男, 江西泰和人, 天津工业大学副教授, 博士, 主要从事凝聚态物理研究工作.

教学研究

O 413.1

A

1000- 0712(2016)04- 0001- 06