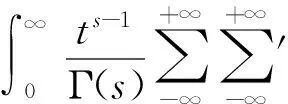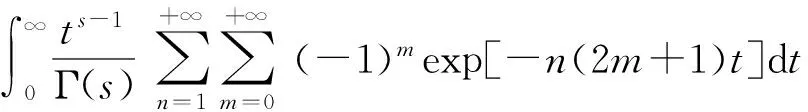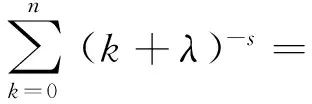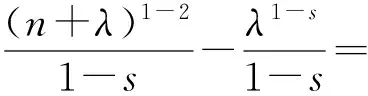两维离子晶体的马德隆常数
邱为钢
(湖州师范学院 理学院,浙江 湖州 313000)
两维离子晶体的马德隆常数
邱为钢
(湖州师范学院 理学院,浙江 湖州313000)
由无穷求和技巧和渐近展开,得到了两维正方形和正六边形晶体马德隆常数的解析表达式.
马德隆常数;无穷求和;正六边形
马德隆常数的物理意义很明确,麻烦的是如何给出解析表达式或者具体数值. 常用的手段是数值计算,文献[1]数值计算了两维正方形晶体的马德隆常数,文献[2]则给出了两维正三角形(正六边形)晶体马德隆常数的数值解. 数值方法简单直观,但要达到需要的数值精度,计算时间一般以小时为计. 如果这两个常数有解析表达式,数学软件马上就可以给出所需精度的数值表示. 我们发现,利用数学上的无穷求和技巧,是可以得到文献[1,2]上两个常数的解析表达式的. 文献[2]中马德隆常数与本文解析值前7位相同,文献[3]中马德隆常数与本文解析值前6位相同,验证了本文所用方法的合理正确性.
设两维格点(晶体)上有固定离子,离子之间的相互作用势是
(1)

定义无量纲的马德隆常数为
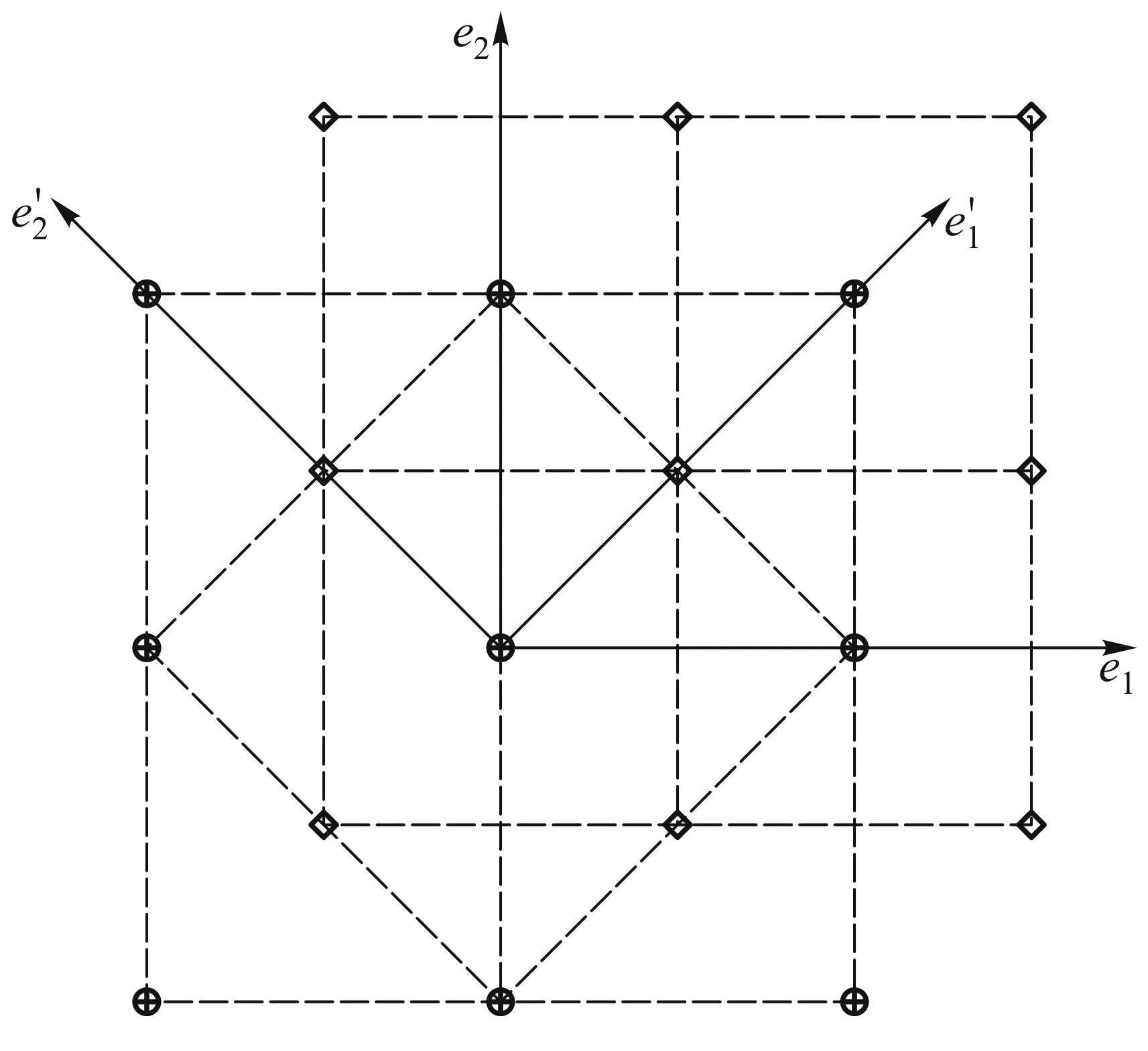
图1 正方形晶体离子分布示意图
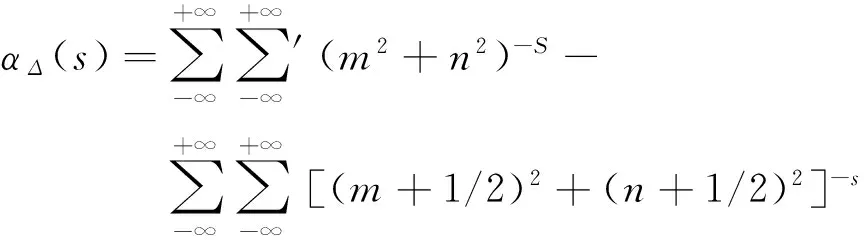
(2)
式(2)中第一个两重无穷求和要扣除(0,0). 当0 (4) 利用单位跃迁函数H(x)[4],可以把式(3)中有限求和化为无穷求和 (5) 其中求和遍及除去原点(0,0).利用跃迁函数积分表示[4]: (6) 以及积分变换公式: (7) 式(5)化为 (8) 令q=exp(-(z+t)),利用两重求和恒等式[5]: (9) 式(8)化为 (10) 继续利用(6)、(7)两式,式(10)化为 (11) 考虑到跃迁函数的作用,式(11)化为 (12) 其中N(R,m)是R2/(2m+1)的整数部分. 在式(7)中,令z=k+λ,两边对k从0到n求和,得到 (13) 同样两边对k从0到n积分,得到 (14) 式(13)减去式(14),并利用Hurwitz Zeta 函数ζ(s,λ)[7]的积分表达式[6]: (15) 得到 0 (16) 当圆半径R趋向无穷大时,利用式(16),式(12)化为 (17) 式(17)可以化为 (18) 式(18)右边的第一项是发散项,随圆半径R增大而增大. 同样,利用两重求和恒等式[5] (19) 沿用以上方法,计算得到 (20) 由此得到正方形晶体马德隆常数解析表达式为 ζ(s,3/4)][ζ(s)-ζ(s,1/2)] (21) (22) 这与文献[3]的数值计算结果一致. 图2 正六边形晶体离子分布示意图 定义无量纲的马德隆常数为 (m+1/3)(n+1/3)]-s (23) 由文献[5]中的两重无穷求和恒等式: (24) (25) 沿用以上方法,计算得到二维正六边形晶体马德隆常数的解析表达式为 αΔ(s)=6×3-sζ(s)[ζ(s,1/3)-ζ(s,2/3)]- 3×6-s{ζ(s,1/3)[ζ(s,1/6)-ζ(s,2/3)]+ ζ(s,2/3)[ζ(s,1/3)-ζ(s,5/6)]} (26) (27) 这与文献[2]的数值计算结果一致. 马德隆常数的数值计算虽然很直接,但是先要按一定规则对晶格划分编号,再手动编写程序,最后输入计算机数值计算,整个过程还是麻烦. 马德隆常数的解析计算只有有限几种情形,包括本文的正方形晶格和正六边形晶格,计算过程中要用到积分表示,积分变换,特殊函数和渐近展开,可以作为数学物理方法在固体物理应用的教学例子之一. [1]刘策军. 二维NaCl晶体马德隆常数计算[J]. 大学物理,1995,14(12): 21-22. [2]黄仕华,徐晶晶. 二维三角离子晶体马德隆常数的计算[J]. 浙江师范大学学报(自然科学版),2007,30(3): 282-286. [3]詹泸成,罗志琳. 离子晶体的马德隆常数计算[EB/OL].北京:中国科技论文在线[2010-05-06].http://www.paper.edu.cn/releasepaper/content/201005-161. [4]跃迁函数[EB/OL]. http://mathworld.wolfram.com/HeavisideStepFunction.html [5]Itzykson C, Luck J M. Arithmetical degeneracies in simple quantum systems[J]. J Phys A: Math Gen,1986,19: 211-239. [6]Srivastava H M,Junesang Choi. Series associated with Zeta and related functions[M]. Kluwer Academic Press,2001: 92-93. [7]王竹溪,郭敦仁. 特殊函数概论[M].北京:北京大学出版社,2000. The Madelung constant of two-dimensional ion crystal QIU Wei-gang (School of Science,Huzhou Teachers College,Huzhou,Zhejiang 313000,China) The analytical expression of Madelung constant of two-dimensional square and hexagon ion crystal is derived from the infinite summation technique and asymptotic expansion method. Madelung constant;infinite summation;hexagon 2015-04-07; 2015-09-17 国家自然科学基金(11475062,11275067)资助. 邱为钢(1975—),男,江苏张家港人,湖州师范学院理学院副教授,博士,主要从事数学物理和大学物理的教学研究工作. 教学讨论 O 481 A 1000- 0712(2016)04- 0019- 03