三维△×n阶电阻网络的两个等效电阻公式
袁 莉,谭志中,彭 菊
(南通大学 理学院,江苏 南通 226019)
三维△×n阶电阻网络的两个等效电阻公式
袁莉,谭志中,彭菊
(南通大学 理学院,江苏 南通226019)
研究了一类三维△×n阶电阻网络在2种不同情形下的等效电阻问题. 采用网络分析方法,通过构建差分方程组模型及矩阵变换,获得了三维△×n阶电阻网络远节点之间的2个等效电阻公式,并具体进行了讨论和验证.
三维△×n阶网络;差分方程;矩阵变换;等效电阻
电阻网络模型具有具体、直观以及便于分析研究等特征,因此电阻网络模型的构建与研究已成为一系列科学问题研究的基本方法之一.许多抽象、复杂的科学问题可以通过构建电阻网络模型进行模拟研究[1-12].电阻网络的等效电阻公式研究一直是一个比较困难的问题[8-11],文献[8]于2004年给出了任意矩形电阻网络在二维和三维情形下的等效电阻公式.尽管如此,由于文献[8]给出的结论表达式比较复杂(因为同一种结果可以有不同的表达方法),不利于具体网络的处理与应用,因而一些具体网络仍然值得我们去研究,以便获得简洁而实用的理论公式. 文献[10]的研究工作为我们提供了新的理论与方法.
非对称情形的三维△×n阶电阻网络问题之前一直没有得到很好地解决. 本文研究了三维△×n阶电阻网络在2种不同情形下的等效电阻,采用文献[1]中建立的递推与变换方法,得到了几个新的结论,并且通过一些特殊情形下的结果对普适公式进行了验证.
研究的三维△×n阶电阻网络模型如图1所示. 该模型的纵向截面是三角形,横向是由n个完全相同的三棱体单元相连而成,其中R、R1、R2和R3是4个任意电阻值,n是0到∞的任意自然数.我们的目的是研究A、B两节点间的等效电阻Rab(n)的普适公式.

图1 三维△×n阶电阻网络模型
1 对称情形下的三维△×n阶网络的等效电阻
在图1结构的三维△×n阶电阻网络模型中,设AA′、BB′、CC′轴线网络单元的电阻均为R,所有三角形结构上的电阻均分别为R1,R2,R3,电阻参数如图1所示.首先考虑对称条件下的情形,即计算R3=R2时的等效电阻Rab(n).在这种情形下,由图1可以看出,AA′行、BB′行对于CC′具有完美的轴对称.无论电流从A输入B输出,还是从B输入A输出,CC′轴上节点的电势都是相等的,也就是说CC′轴中没有电流通过,这样CC′行中的电阻就算拆除也不会影响Rab(n). 由此,在仅求A、B两节点间的等效电阻Rab(n)时,可以将图1所示的三维△×n电阻网络结构等效为图2所示的二维平面n阶电阻网络模型.

图2 二维△×n阶电阻网络等效模型
根据并联电阻的计算方法,可以很快得到图2平面网络结构中的电阻R0=R1//(2R2)(其中R1、R2的阻值已知).
特别指出,对于m×n阶网络的最简单形式1×n阶电阻网络,如图2所示,它实际上是一种特殊的二端梯形网络. 设左端A、B端为输入端,且输入端等效电阻为Rab(n). 这一二维平面模型的等效电阻可以由文献[1,2]中的结论直接得到
(1)
其中R0=R1//(2R2)=2R1R2/(R1+2R2),且α,β分别是方程
x2=2(1+R/R0)x-1
(2)
的两个根. 解此方程得
(3)
另外,文献[1]定义了一种tz(α,n)函数,
(4)
据此,可将等效电阻Rab(n)重新简单地表示成
Rab(n)=[1-tz(α,n)]R0
(5)
式(1)、(5)即为三维△×n阶网络等效电阻Rab(n)的普适公式. 此二式对于n=0,1,2,…的一切自然数都是成立的.
注意:式(1)、(5)给出的目的是为了下文验证非对称情形下的等效电阻公式的正确性,同时也是为了说明特殊条件下的问题可以采用特殊的简单方法求解.
1.1具体讨论与比较
1) 在图1中,当n→∞时,该网络被称为三维无穷△×n阶电阻网络. 由式(4)取极限易得
(6)
所以由式(1)取极限易得
(7)
其中R0=R1//(2R2),式(7)即为三维无穷△×n阶电阻网络A、B两节点间的等效电阻的普适公式. 此时的等效电阻Rab(∞)是有限常数,并且是由无理式表示的结果.
2) 当图1中的阶数n=0时,该网络简化成为图3所示的三维0阶电阻网络(退化成平面的三角形).由式(5)得到
Rab(0)=R0=2R1R2/(R1+2R2)
(8)
此与图3所示的实际电路计算得到的等效电阻完全一致,说明式(5)包括了n=0时的情况.
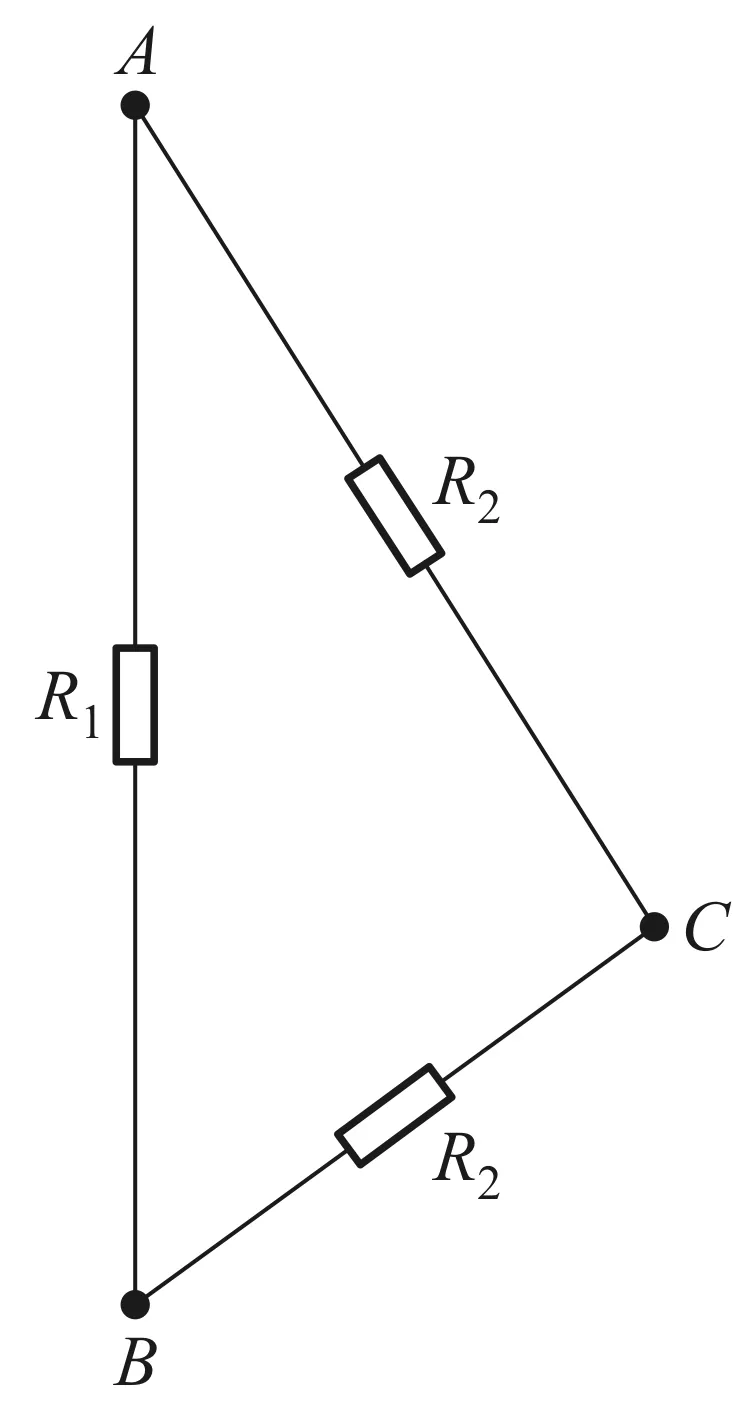
图3 △×0阶网络模型
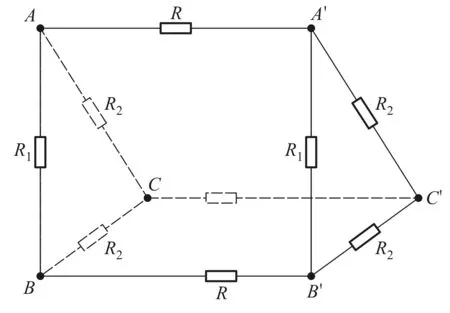
图4 △×1阶网络模型
3) 当图1中的n=1时,该网络退化成为图4所示的三维三角形1阶电阻网络,由理论式(1)得到
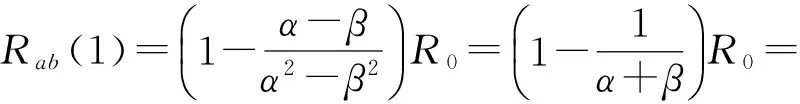
(9)
这与由图4所示的实际电路计算得到的等效电阻Rab(n)完全一致(此处实际计算略),表明在n=1时式(5)是正确的.
2 非对称情形下的三维△×n阶网络的等效电阻
当R3=R1时,对于节点A和B而言,图1结构的三维△×n阶电阻网络不再对称.下面具体计算这种情形下的三维非对称结构的△×n阶网络的等效电阻,研究A、B两节点间的等效电阻Rab(n)的普适公式.
2.1电阻网络中的电流规律
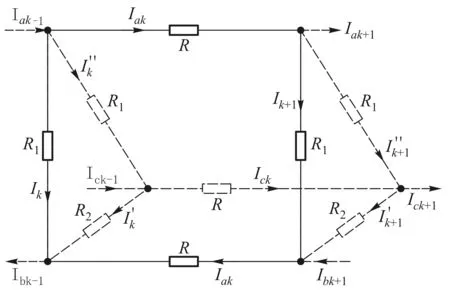
图5 △×n阶子电阻网络模型
采用网络分析方法,对图5中的子网络进行节点电流分析和网孔电压分析,得到差分方程组模型:
(10)
(11)
式(11)是一元差分方程,由式(11)得到特征方程:
(12)
设关于x的方程的两根分别为α、β,解方程(12)得
(13)
根据文献[1,12 ]中的方法解差分方程(11)得到
(14)
式(14)即为任意子网络中通过纵向电阻R2的电流通用规律.
另外,将式(10)、式(11)写成矩阵形式的差分方程组模型:
(15)
将矩阵式(15)左乘一个二阶待定矩阵,得到
(16)
其中P为式(15)中的系数二阶矩阵. 设存在常数t1、t2,使得
(17)
将式(17)的左端和右端展开,得到
(18)
根据式(18)为恒等式,可确定λ1、λ2、t1、t2的具体值为
(19)
所以,矩阵方程(18)可以转化成
(20)
由方程(20)得差分矩阵方程的特征方程:
y2=ty-1
(21)
设关于y的方程的两根分别为γ、δ,由式(21)解得
(22)

(23)
式(23)即为任意子网络中通过截面三角形电阻R1、R2的电流通用规律.
2.2边界电流条件约束
当电流从A输入至B输出时,根据电流的连续性方程由图5、图6可知
(24)
(25)
所以,由式(24)、式(25)得到
(26)
(27)

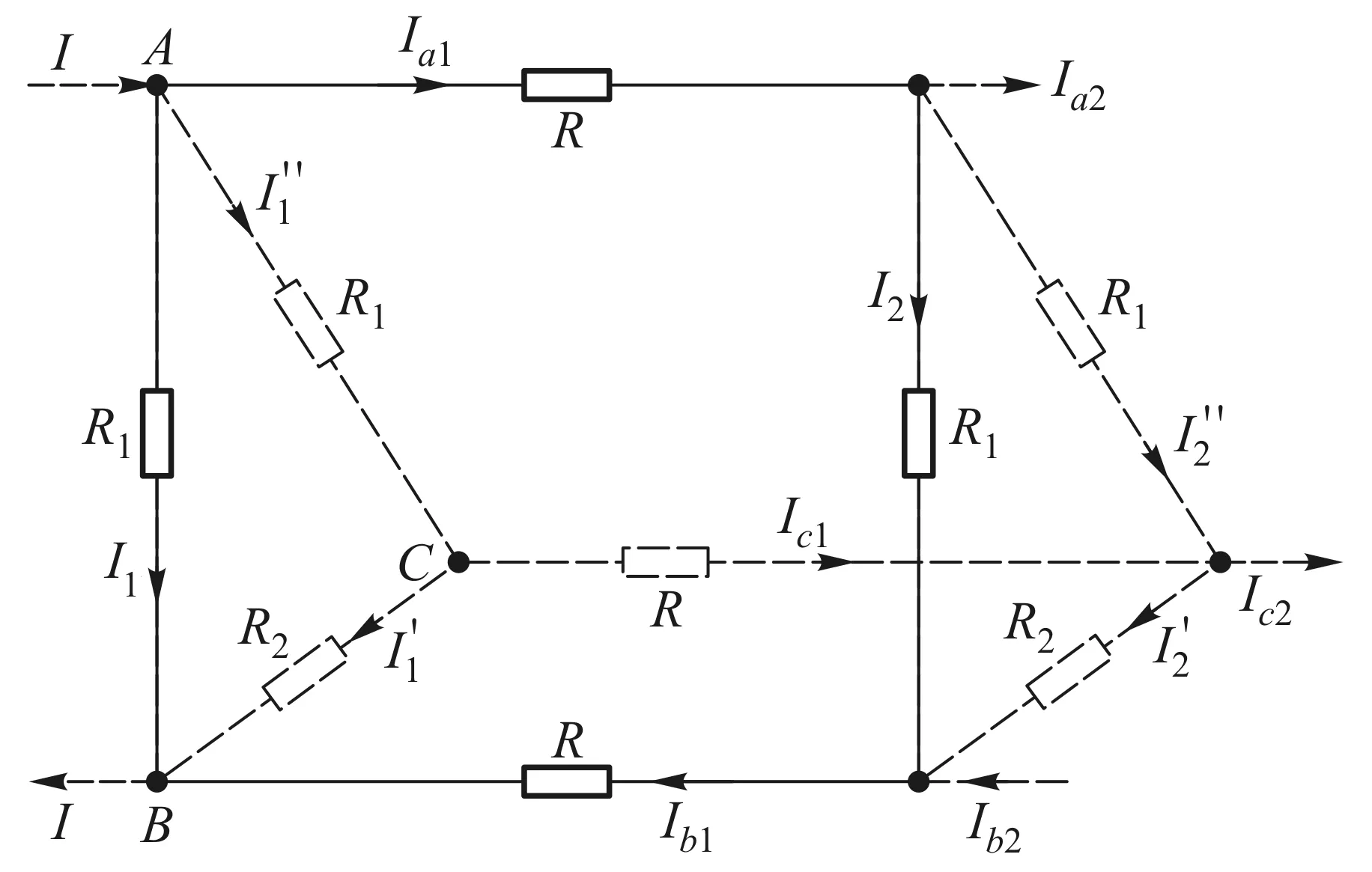
图6 △×n阶电阻网络左边界条件
(28)
分别将式(23)、式(14)从k=1到n+1求和,并应用式(28)及式(26)得到
(29)
(30)
根据网络分析方法,由图6得左边界电流参数的方程组:
Ia1R+I2R1+Ib1R-I1R1=0
(31)
(32)
Ia1R+I″2R1-Ic1R-I″1R1=0
(33)
对截面三角形进行网孔电压分析,可得差分方程:
(34)
由图6得左边界节点电流方程组:
(35)
解以上诸式,并且化简、整理得到
(36)
(37)
根据式(36)、式(37)得到
(38)
(39)
将式(38)代入式(29),解方程得到
(40)

(41)
将式(39)代入式(30),解方程得到
(42)
式(41)、式(42)即为图1中电流从A输入至B输出时的边界电流普适公式.
2.3计算等效电阻Rab(n)
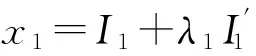
(43)
其中α、β、γ、δ分别由式(13)、式(22)确定. 式(43)即为A、B两节点间的等效电阻Rab(n)的普适公式.
特殊情形下,当R2=R1时,得到(α,β)=(γ,δ),则式(43)退化为
(44)
当R2=R1时,式(44)与式(1)的值完全相同,这也相互验证了彼此的正确性.
另外,根据式(4)定义的tz(n,x)新函数可以将等效电阻Rab(n)重新表示成
(45)
其中,式(45)满足n=0,1,2,…的一切自然数.
3 结束语
采用网络分析方法,通过构建差分方程组模型及矩阵变换,首次获得了三维△×n阶电阻网络的两个等效电阻公式. 研究表明,非对称条件下的三维△×n阶电阻网络等效电阻的研究比较复杂,但是我们得到的结论是比较简单的. 所得到的式(1)、(5)、(44)、(45)等效电阻公式是普适规律,对于一切自然数n=0,1,2,…均成立. 本文采用的研究方法具备创新性,这对教学中培养学生逻辑推理和创新思维能力,乃至科研上推动其他三维网络的研究都具有积极意义.
[1]谭志中. 电阻网络模型[M]. 西安:西安电子科技大学出版社,2011:16-236.
[2]谭志中,陆建隆. 二端梯形网络等效复阻抗的普适研究[J]. 大学物理,2009,28(7): 29-33.
[3]谭志中,方靖淮. 3×n阶电阻网络等效电阻的研究[J]. 大学物理,2008,27(9): 7-10.
[4]谭志中,罗达峰. 4×n阶网络的2个等效电阻公式[J]. 南通大学学报(自然科学版),2011,10(3):87-94.
[5]谭志中,周玲,李颂. 三维□×n阶网络等效电阻的普适公式[J]. 河北师范大学学报,2012,36(4):369-380.
[6]谭志中,陆建隆. 三维立方形n阶电阻网络等效模型构建[J]. 杭州师范大学学报(自然科学版),2010,9(6):464-467.
[7]谭震,谭志中. 构建等效模型研究三维网络的等效电阻及复阻抗[J]. 大学物理,2014,33(5): 53-62.
[8] Wu F Y. Theory of resistor networks: the two-point resistance [J].Journal of Physics A: Mathematical and General,2004,37(26): 6653-6673.
[9] Tan Zhi-Zhong, Essam J W, Wu F Y.Two-point resistance of a resistor network embedded on a globe [J]. Physical Review E,2014,90: 012130.
[10] Tan Zhi-Zhong. Recursion-Transform approach to compute the resistance of a resistor network with an arbitrary boundary[J]. Chinese Physics B,2015,24(2):020503.
[11] Tan Zhi-Zhong,Fang Jing-Huai. Two-point resistance of a cobweb network with a 2rboundary[J]. Communications in Theoretical Physics,2015,63: 36-44.
[12] 谭志中. 二阶方阵次幂的普适公式及应用[J]. 南通大学学报(自然科学版),2012,11(1):87-94.
Two equivalent resistance formulas of 3D △×n network
YUAN Li, TAN Zhi-zhong, PENG Ju
(School of Science, Nantong University, Nantong, Jiangsu 226019, China)
Under various conditions, an equivalent resistance of 3D △×n network is studied. By establishing model of differential equations and matrix transformation in terms of network analysis, we have found two equivalent resistance formulas between two remote nodes of 3D △×n network. The equivalent resistance can be specifically discussed and confirmed.
3D △×n network; differential equation; matrix transformation; equivalent resistance
2015-07-18;
2015-11-20
袁莉(1979—),女,江苏南通人,南通大学理学院讲师,工学硕士,主要从事物理教学与研究工作.
TM 131
A
1000- 0712(2016)04- 0022- 04

