参数微扰法计算氦原子基态能量

陆　霁，李天乐，席　伟，张昌莘

(广东石油化工学院 物理系，广东 茂名　525000)



参数微扰法计算氦原子基态能量

陆霁，李天乐，席伟，张昌莘

(广东石油化工学院 物理系，广东 茂名525000)

氦原子；参数微扰法；基态能量

计算氦原子的基态能量，常用的方法是变分法.为了提高计算的精确度，通常选取多个变分参数，如文献[1]考虑了氦原子中两个电子的径向排斥作用，选择两个参数的试探波函数，应用变分法并通过Mathematica5.0 软件编写程序计算了氦原子的基态能量.文献[2]选择两个参数，利用编制的Fortran 程序，通过基态氦原子RHF方程进行数值解，得到氦原子的基态能量.文献[3]考虑氦原子的两电子之间关联效应，选择包含关联坐标的试探波函数，应用变分法计算得到氦原子的基态能量.文献[4]选择4个变分参数，应用MATLAB 7.0软件计算得到氦原子的基态能量.通过多参数变分法计算得到的氦原子的基态能量比文献[5，6]应用一个变分参数得到的结果更加接近实验值.

微扰法虽然能够计算氦原子基态能量，但是由于氦原子中两个电子的相互作用能不是一个很小的微扰项，计算结果与实验值相差较大[5，6].因此微扰法不是计算氦原子基态能量的一个好的方法.为了能够应用微扰法计算氦原子基态能量，笔者在文献[7]中引入一个屏蔽参数，建立了含有屏蔽参数的类氦原子哈密顿方程，提出计算类氦原子基态能量的参数微扰法.

1　含有屏蔽参数σ的氦原子哈密顿算符本征方程

根据文献[7]可知，有1个屏蔽效应参数σ的氦原子的哈密顿算符为

(1)

(2)

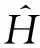
(3)

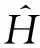
Φ(r1,r2,s1z,s2z,σ)=ψ(r1,r2,σ)χ(s1z,s2z)

(4)

氦原子的本征方程为

(5)

2　氦原子的基态能量E和基态波函数ψ(r1,r2)

2.1氦原子基态近似波函数修正ψ(n)(r1,r2,σ)

选取氦原子基态零级近似波函数和n级近似波函数修正ψ(n)(r1,r2,σ)分别为两个电子分别处于有效核电荷数为Z*=2-σ的类氢原子的基态1s和激发态ns(n=1,2,3,…)组合的双电子波函数.本文选取波函数ψ(n)(r1,r2,σ)为

(6)

ψ100(r2,σ)ψ200(r1,σ)]

(7)

ψ100(r2,σ)ψ300(r1,σ)]

(8)

ψ(3)(r1,r2,σ)=ψ100(r1,σ)ψ400(r2,σ)

(9)

其中

(10)

(11)

(12)

(13)

氦原子基态近似波函数的修正ψ(1)(r1,r2,σ)～ψ(4)(r1,r2,σ)是正交归一化波函数，与零级近似波函数ψ(0)(r1,r2,σ)相互正交.

2.2氦原子基态零级近似能量E(0)和能量修正值E(1)(σ)～E(4)(σ)

氦原子基态零级近似能量E(0)是两个有效核电荷数为z*=2-σ的类氢原子基态能量之和，即

(14)

应用积分公式[5]

(15)

(16)

(17)

(18)

(19)

2.3氦原子基态能量E和基态波函数ψ(r1,r2)

根据参数微扰法，含有屏蔽参数σ的氦原子基态能量为

E(σ)=

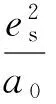
(20)

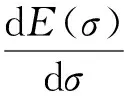
σ=0.618422517，Z*=2-σ=1.381577483

(21)

将氦原子屏蔽参数σ=0.618422517和有效核电荷数Z*=1.381577483分别代入式(20)，得到氦原子基态能量E为

(22)

作为参数微扰法和变分法计算氦原子基态能量的比较，在表1中列出了部分参考文献应用变分法计算的氦原子的基态能量值.在表1中，ΔE是氦原子基态能量理论值与实验值的误差.

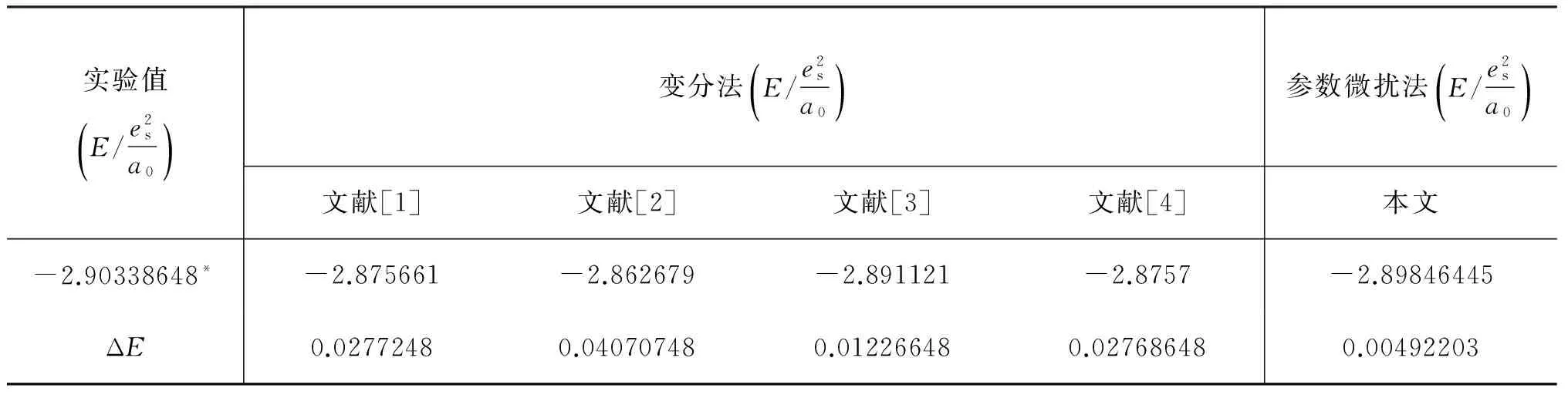
表1　参数微扰法与变分法计算氦原子基态能量的比较

*氦原子基态能量实验值取自于文献[8]

ψ100(r2)ψ300(r1)]+ψ100(r1)ψ400(r2)

(23)

3　结束语

应用参数微扰法计算氦原子的基态能量，在计算到4级近似能量时，就得到与实验值误差很小的理论值.参数微扰法中引入的屏蔽参数与变分法引入的变分参数相比，具有更加明确的物理意义.在参数微扰法中选取的基态波函数是正交归一化波函数.参数微扰法计算氦原子基态能量不需要计算机编程，计算过程简单.并且随着近似波函数级数的增加，计算结果与实验值误差会越来越小.参数微扰法是计算多电子原子能级的一种有效方法.

[1]于凤军.氦原子及类氦离子基态的二参数变分法研究[J].大学物理，2008，27(5)：1-3.

[2]陈冠军.氦原子基态能量的Roothaan-Hartree-Fock计算[J].大学物理，2010，29(12)：7-9.

[3]马二俊.类氦原子体系基态能量的双参数变分计算[J].大学物理，2012，31(10)：18-21.

[4]胡先权,马勇,殷霖,等.四参数法计算氦原子基态能级研究[J]. 原子与分子物理学报,2006,23(6): 1045.

[5]周世勋，陈灏.量子力学教程[M].2版.北京: 高等教育出版社, 2009：130-133，202-205.

[6]曾谨言.量子力学教程[M].2版.北京：科学出版社，2008：176，226.

[7]张昌莘，宁土荣，陆霁.研究类氦原子基态能量的参数微扰法[J]. 大学物理，2015，34(2)：32-34.

[8]刘玉孝,赵振华,王永强，等.氦原子和类氦离子基态能量的变分计算及相对论修正[J].物理学报,2005,54(6)：2620-2624.

Calculation of ground state energy of the helium atom by parameter perturbation method

LU Ji, LI Tian-le, XI Wei, ZHANG Chang-xin

(Department of Physics, Guangdong University of Petrochemical Technology, Maoming，Guangdong 525000, China)

helium atom;parameter perturbation method; ground state energy

2015-06-30；

2015-12-06

国家自然科学基金项目( 91121019)、广东省科技计划项目(2010B080701066)资助

陆霁(1972—)，女，广东汕头人，广东石油化工学院物理系讲师，主要从事物理教学和研究工作.

张昌莘，E-mail:zcx2923018@163.com

O 413.1

A

1000- 0712(2016)08- 0036- 03