二维光栅衍射图样的特性分析

于凤军

(安阳师范学院 物理与电气工程学院，河南 安阳　455000)



二维光栅衍射图样的特性分析

于凤军

(安阳师范学院 物理与电气工程学院，河南 安阳455000)

导出二维光栅衍射光斑的位置公式，讨论其衍射图样的特性，并给出实验演示效果. 提出一种通过衍射图样照片测量光栅常数(或波长)的方法.

二维光栅；衍射图样；特性；实验演示；光栅常数

在一块不透明的平板上钻很多行、很多列的小圆孔，让小孔排列成正方或长方点阵形式，构成一块二维光栅. 市场上有一种激光玩具，它包含一个激光笔和二维光栅，用它可以演示二维光栅的衍射效果，如图1. 对于这种衍射图样的特性，目前大部分教材[1-3]上定性的描述为二维点阵分布，本文推导二维光栅衍射光斑的位置公式，并定量分析其衍射图样的特性.

图1

1　衍射光斑位置分布的计算

如图2所示，用黑色小圆点表示小圆孔，取原点O在光栅平面的中心，x轴沿小孔点阵的列方向，y轴沿小孔点阵的行方向，z轴垂直于光栅平面，建立坐标系Oxyz.设在x和y方向，相邻小孔中心的距离分别为a、b(以下称a、b为光栅常数，).让一束激光的中心通过原点、沿z轴正方向射向光栅，让接收屏P与光栅平面平行地放在z=L处，并使L远大于激光束的截面直径或远大于光栅表面的线度(图1属于这种情况).

图2

我们采用夫琅禾费衍射模型进行计算，理由是激光束非常接近平行光束，并且L远大于光栅表面的线度，以致从光栅表面各点向屏P上同一点发出的衍射线方向几乎是相同的，可以近似地把这些衍射线看作是平行的，按上述模型计算不会带来多大的误差.

图1中使用的光的波长是0.532 μm，光栅常数为5.95 μm，使用的激光束的截面直径约为1 mm，即激光光斑大小约为1 mm，它大约可以覆盖168个光栅周期.假设激光光斑可以覆盖到N0个小圆孔，则从每个被照射的小孔射出的光线都会按照夫琅禾费衍射的规律沿不同的方向散开. 考虑从各个被照射小孔中心发出的、朝着同一方向射出的N0束光线，若它们相互之间的光程差都等于波长的整数倍，则光栅在该方向的出射光将达到衍射主极大. 假设光栅的出射光沿着它与x轴夹角是α、与y轴夹角是β的方向已经达到衍射主极大，则由图2可以看出，这时从x轴上(或y轴上)任二个相邻小孔中心射出的光线光程差都等于波长的整数倍，即

(1)

设满足式(1)的出射光束与z轴的夹角为γ，则该光束的中心光线所对应的直线方程为

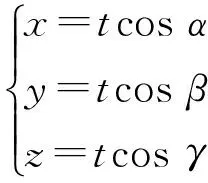
(2)其中t为参数. 令上式中z=L(即屏P的平面方程)， 则由几何条件cos2α+cos2β+cos2γ=1和式(1)、式(2)，得到该直线与屏幕的交点——衍射光斑中心的位置坐标

(m1，m2=0，±1，±2，…)

(3)

式(3)表明，x、y都与距离L成正比，所以改变L仅使衍射图样的整体放大或缩小，而波长与光栅常数的比值λ/a和λ/b将决定衍射斑点分布的几何形态. 当a、b、λ、L给定后，将m1、m2的具体数值代入式(3)可以计算屏P上各光斑的中心位置.

另外，从光栅公式[1-3]dsinθ=nλ出发也可以导出式(3). 其思路是把二维光栅中各个小孔看作由很多不同方向的平行线构成，图3中标出了其中4组，将每一组平行线等价地看作一个一维“光栅”(各“光栅”的d不相同). 先计算每个“光栅”的衍射光斑位置，然后把各个“光栅”的衍射光斑进行汇总.

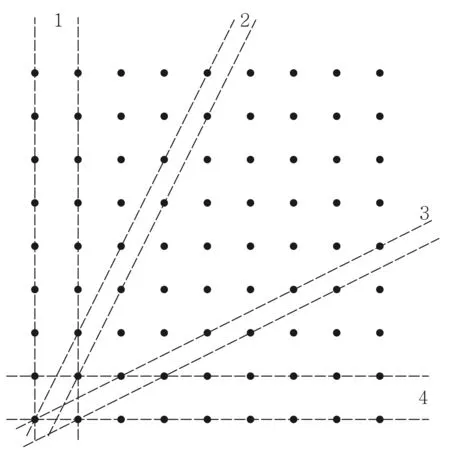
图3

2　关于衍射图样特性的讨论

这里以图1中使用的激光和光栅数据为例进行衍射图样的计算，即令λ=0.532 μm，a=b=5.95 μm， 取L=1 m，用Mathematica软件计算式(3)，可得到各光斑的中心坐标，再用ListPlot命令作图(见图4). 下面作3点讨论.

图4

1) 关于衍射图样的形状. 由图4可以看出，二维光栅的衍射斑点呈现出对称的、二维点阵分布形式，且在中心附近区域近似为方阵分布，在偏离中心较远的区域，呈现“枕形”分布 (类似于透镜成像的枕形失真). 换个角度讲，设想把衍射图中的某行(或某列)斑点连接成光滑曲线，可以发现：在中心附近区域，它们几乎是直线；在偏离中心较远的区域，它们似乎是双曲线. 下面解释这一现象.

设m1、m2都比较小(即在中心附近区域)，以致条件m1λ/a<<1，m2λ/b<<1得到满足，略去式(3)中关于它们的二次项，得

(4)

上式中x和y与m1、m2分别成正比(或呈线性变化)，导致在行(或列)方向相邻点的间隔相等 (分别是Lλ/a、Lλ/b)，故在这种情况下，亮点分布近似呈现方阵形式. 还可以看出，当λ/a和λ/b较小时，满足上述条件的m1、m2的个数就较多，方阵中的亮点个数较多.

当m1、m2都比较大(即在偏离中心较远的区域)，条件m1λ/a<<1，m2λ/b<<1不满足时，式(3)中x和y与m1、m2分别呈非线性变化关系，所以点阵分布不再呈现方阵形式. 将式(3) 中m2消去，可得方程

(5)

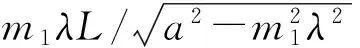
(6)

2) 关于衍射斑的数量. 每个衍射斑点与能使式(3)分母有意义的一对整数(m1、m2)对应，即

(7)

在m1、m2组成的直角坐标系中，每一对整数(m1、m2)对应一个点 (见图5)，满足式(7)的点都在半长轴为a/λ、半短轴为b/λ的椭圆内. 显然a/λ和b/λ越大，衍射斑数量越多，衍射斑点与该椭圆内的点存在映射关系， 理论上图4中的斑点的数量等于该椭圆内的点数.

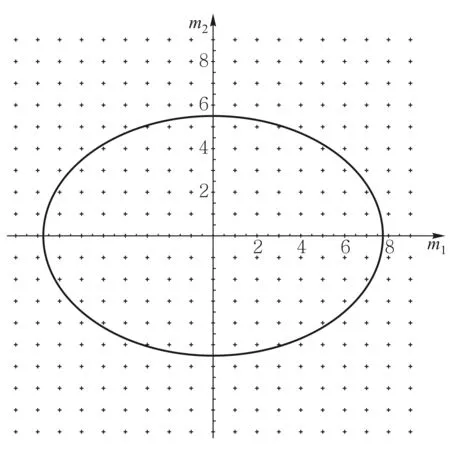
图5

然而，实际看到的衍射光斑(见图1)的数量比图4中的斑点少许多.解释如下：图4是仅按照孔间干涉计算的，没有考虑孔间干涉的强度分布会受到圆孔夫琅禾费衍射因子的调制(类似于多缝夫琅禾费衍射时，缝间干涉条纹的分布要受到单缝衍射因子的调制[1，2])问题. 但实际上存在调制作用，位于圆孔衍射的爱里斑内的光斑才是清晰可见的，所以实际看到的衍射光斑的数量比图4中的少许多. 例如，在图6照片中，圆形光晕部分就是圆孔衍射的爱里斑，诸多小亮点确实位于其中，爱里斑之外很难发现有小亮点. 顺便补充说明，在同等条件下，如果圆孔半径r比较大，则爱里斑比较小，人们仅能看见中心附近区域的亮点，亮点分布呈现方阵形式.

3) 关于计算图样与实际图样的对比问题. 用手机或数码相机把实际图样拍成照片(例如，图6)，然后拷贝到电脑. 使用windows系统自带的画图软件，把图4的图样与照片进行重合度对比，发现经过适当缩放后二者基本重合. 作二点补充说明：① 为了减少照片的失真，必须让零级衍射光束尽可能与屏幕垂直，并且尽可能地让照相机镜头的光轴垂直于屏幕，对准零级衍射斑. 只有这样，重合程度才能较高. ② 因个别衍射斑点距原点太远，图4 中未标出；图6中的光斑数目比图4中的斑点数目少许多，在进行重合度比较时仅考虑图4中的斑点与图6中对应的光斑是否重合.

图6

3　光栅常数(或波长)的测量

显而易见的测量方案是通过测量衍射角并利用式(1)来确定光栅的常数或者波长(注：已知某一个确定另一个)，其中衍射角是通过衍射主极大的位置和光栅与屏P的距离测定的. 另一种方案是通过衍射图样的照片. 照片与实际衍射图相比只改变大小、而不改变光斑分布的几何形态，而几何形态由比值λ/a和λ/b决定，所以通过照片应该能够测量该比值，进而确定光栅常数(或波长).

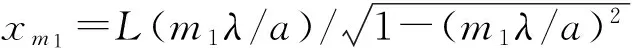
(8)

从上边方程中解出λ/a

(9)

(10)由于式(10)右边的分母正比于xm、xk的平方差，所以η对于m和k的差比较敏感：当m和k二者相差较大时，分母较大而η较小；当二者相差不大、但都较大时，由于非线性特性，分母同样较大而η较小；当二者都较小时，分母较小而η较大. 这些结论可以用上边给出的xm数据代入式(10)进行验证. 至于m和k应该大于何值更好，从式(10)出发难以定量估计.

还有一种更基本的处理方法. 上边的8个xm共有28种组合，λ/a共有28个计算值，采用肖维涅准则逐步删除其中的所有异常数据，最后将剩下的非异常数据求平均值，所得结果与前面的结果在误差范围内是一致的.

小结：以上推导出二维光栅衍射光斑的位置公式，分析了其衍射图样的特性，同时给出了一种利用衍射图样照片测量光栅常数(或波长)的方案. 指出：在较大的范围内衍射图样呈现双曲形亮点阵列分布；当m1λ/a<<1，m2λ/b<<1时，衍射图样近似呈现方阵分布.

[1]赵凯华. 新概念物理教程：光学[M].北京：高等教育出版社，2004.

[2]姚启均. 光学教程[M].北京：高等教育出版社，1981.

[3]母国光. 光学[M].北京：人民教育出版社，1978.

The characteristic analysis of the diffraction pattern of two-dimensional grating

YU Feng-jun

(College of Physics and Electrical Engineering， Anyang Normal University， Anyang， Henan 455000， China)

The position formula for the diffractive light-spot of two-dimensional grating is derived. The property of diffraction pattern is discussed and its experimental demonstration is given. A new method of measurement of grating constant is presented.

two-dimensional grating；diffraction pattern; property; experimental demonstration；grating constant

2015-05-07；

2016-01-12

国家自然科学基金资助项目(11475004)

于凤军(1959—)，男，河南安阳人，安阳师范学院物理与电气工程学院教授，主要从事理论物理、天体力学研究和教学工作.

O 436.1

A

1000- 0712(2016)08- 0032- 04