对量纲法求分形物体转动惯量的再思考
方 伟 , 涂 泓 , 冯 杰
(1. 上海师范大学 物理系,上海 200234;2. 上海市星系和宇宙学半解析研究重点实验室,上海 200234)
对量纲法求分形物体转动惯量的再思考
方伟1,2, 涂泓1,2, 冯杰1
(1. 上海师范大学 物理系,上海200234;2. 上海市星系和宇宙学半解析研究重点实验室,上海200234)
指出数学上无穷阶的分形与物理上可实现的有限阶分形物体之间的差别.利用n阶分形三角形与n-1阶分形三角形的相似性,根据标度变换和量纲分析法,得到n阶分形三角形转动惯量的递推公式,进而得到转动惯量的最终表达式.该结果在n趋向无穷大时与无穷阶分形物体的结果一致.
量纲分析;分形;转动惯量;递推法
求具有一定大小的规则物体的转动惯量是大学物理力学刚体部分的重要内容,其关键在于如何正确确定物体的线元、面元或体积元,进而利用微积分求得.但在学习微积分知识之前,采用这种方法求解具有一定的困难.文献[1]利用量纲分析的方法,对诸如细棒、平面体(三角形、矩形、等腰梯形、正多边形、扇形、圆形等)、长方体等具有一定对称性且质量分布均匀的物体进行标度变换,再结合平行轴定理,进而可以在不用微积分等繁杂运算的情况下求出该物体的转动惯量.该方法思路简单巧妙,物理图像清晰,更重要的是能让学生学着用物理学家的思考方式来考虑问题[2],这对于培养学生的物理思维能力具有重要意义.
许佳敏等[5]将上述方法推广至分形物体,利用分形物体的自相似特性,结合量纲分析、标度变换和平行轴定理分别求出了谢尔宾斯三角形(分形三角形,图1 (a))、门格海绵(分形立方体,图1 (b))、谢尔宾斯四面体(分形四面体,图1 (c))等分形物体的转动惯量.对于分形正三角形,绕通过其质心且垂直于分形三角形平面的转轴的转动惯量为mL2/12(L为分形三角形的边长).对于分形立方体和分形正四面体,绕通过其质心的对称轴的转动惯量分别为mL2/5和mL2/12(L为分形立方体或分形正四面体的边长).
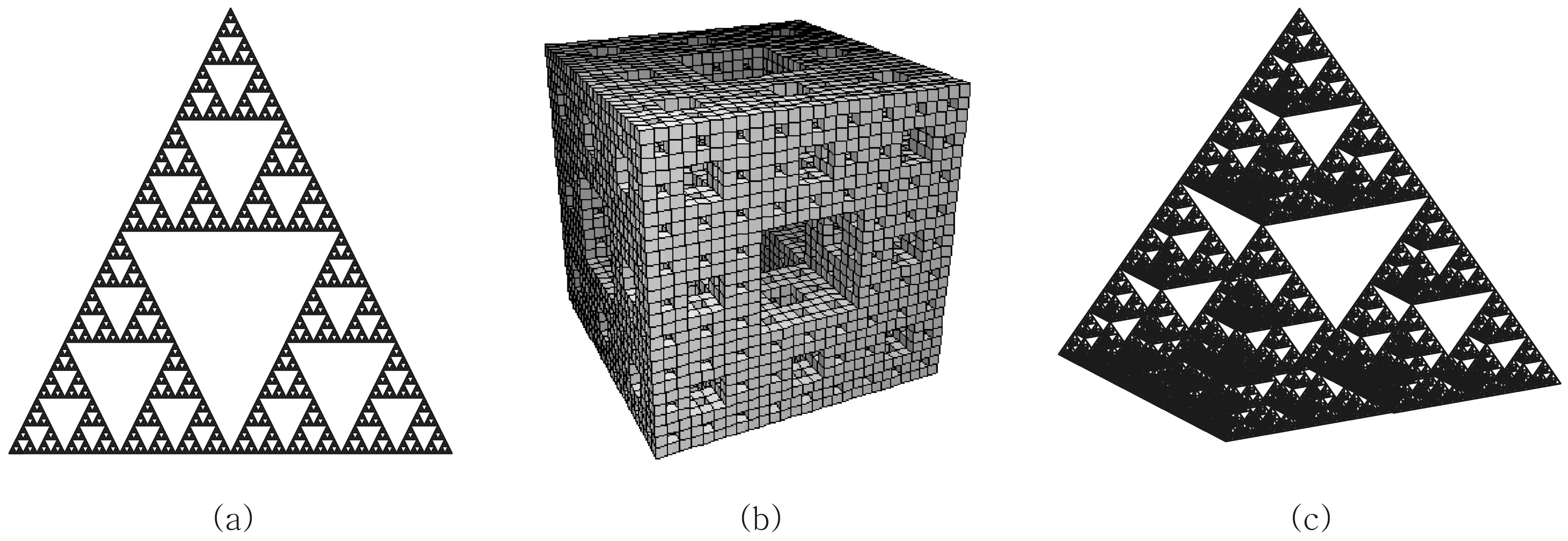
图1
该方法物理动机明确、推广巧妙、思路清晰、结果简明.不过深入研究后不难发现,将此方法直接推广至无限阶分形物体产生了一个难以理解的问题,那就是对于无限阶的分形三角形面积为0,对于无限阶的分形立方体和分形四面体体积为0,因而它们三个分形物体的质量m均为0,此时按照定义转动惯量也应为0.下面我们以分形正三角形为例来具体说明该问题,然后给出解决方案,并证明在极限情况下,该方法给出的结果和文献[5]的结论一致.
1 物理分形与数学分形的区别

2 递推法求物理分形物体的转动惯量
应该如何求解实际的分形物体的转动惯量呢?我们首先定义n阶的物理分形物体:如图2所示,定义图2 (b)为1阶分形三角形,图2 (c)、图2 (d)分别为第2阶和第3阶分形三角形,图2 (a)因而可以看成是第0阶的分形三角形,n阶的分形三角形可以依此类推.
如前所述,物理分形三角形(即n阶的分形三角形)其部分与整体并不严格相似,如将图2(d)中的A3B3C3线度放大为原来的两倍之后,得到的图形并不与图2(d)本身重合,但是A3B3C3放大为原来的两倍后却与图2 (c)重合.更进一步说,n阶分形三角形的AnBnCn在线度翻倍后均与其上一阶(即n-1阶)的分形三角形重合,因而第n阶的分形三角形可以看成是由三个n-1阶的分形三角形在线度缩小一半之后拼出来的,于是就有可能通过上下两阶分形三角形的相似特性(注意:非n阶分形三角形的自相似性),结合量纲分析、标度变换和平行轴定理推导出n阶分形三角形的递推公式,最终求出n阶分形三角形绕通过其质心且垂直于分形三角形平面的转轴的转动惯量.
设图2 (a)是质量为m,边长为L的正三角形平板,它绕通过其质心O且垂直于分形三角形平面的转轴的转动惯量为I0.
该图进行一次分形后得到1阶物理分形三角形(图2 (b)),此1阶分形三角形的质量m1显然等于3m/4.设图2 (b)绕通过其质心O且垂直于分形三角形平面的转轴的转动惯量为I1.图2 (b)可以看成三个线度为图2 (a)一半的三角形A1B1C1绕质心轴O的转动惯量的叠加.三角形A1B1C1绕质心轴O的转动惯量则是A1B1C1绕自身质心轴O’的转动惯量再通过平行轴定理得到.根据量纲分析、标度变换和平行轴定理有
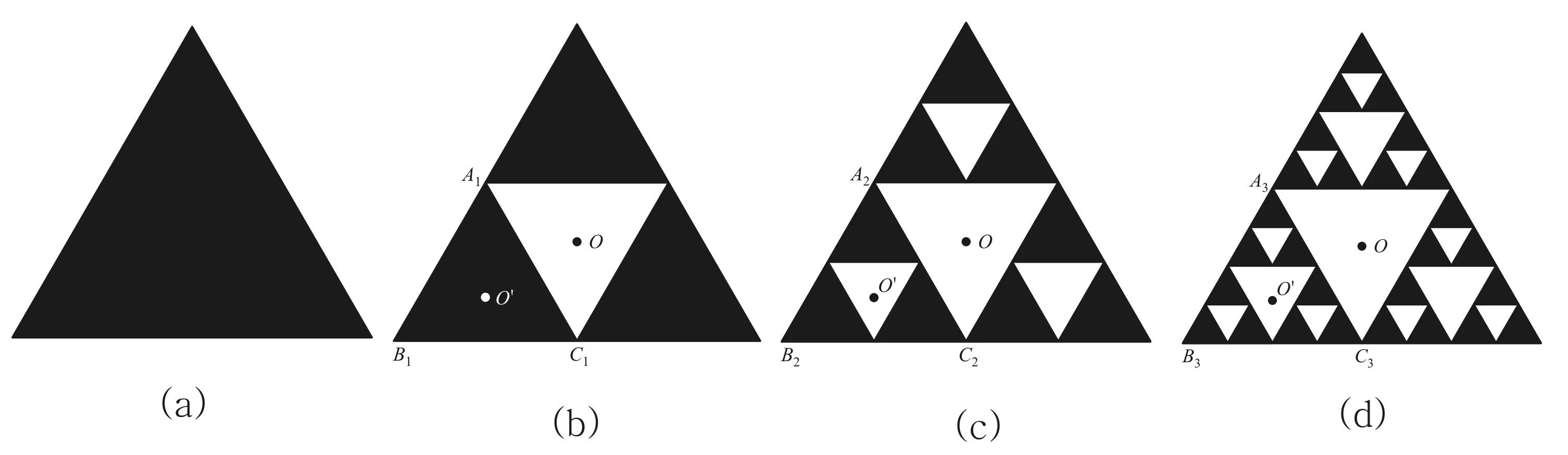
图2
(1)
再次分形后得到2阶分形三角形(图2 (c)),此2阶分形图的质量m2显然等于(3/4)2m.设图2 (c)绕通过其质心O且垂直于分形三角形平面的转轴的转动惯量为I2.图2 (c)可以看成三个线度为图2 (b)一半的1阶分形三角形A2B2C2绕质心轴O的转动惯量的叠加.根据量纲分析、标度变换和平行轴定理有
(2)
同理,再次分形后得到3阶分形三角形(图2 (d)),此3阶分形三角形的质量m3等于(3/4)3m.设图2 (d)绕通过其质心O且垂直于分形三角形平面的转轴的转动惯量为I3.图2 (d)可以看成三个线度为图2 (c)一半的2阶分形三角形A3B3C3绕质心轴O的转动惯量的叠加.根据量纲分析、标度变换和平行轴定理有
(3)
由此类推,不难得到第n阶物理分形三角形的质量mn等于(3/4)nm.该分形三角形绕通过其质心O且垂直于分形三角形平面的转轴的转动惯量为In,可以看成三个线度为n-1阶分形三角形An-1Bn-1Cn-1一半的分形三角形绕质心轴O的转动惯量的叠加.根据量纲分析、标度变换和平行轴定理有
(4)
为求n阶分形三角形转动惯量最终的表达式,将上式改写为
(5)

(6)
当n→∞时,In=0,也即本文开篇所说的,对于数学分形三角形,其质量为0,转动惯量也等于0.
由于式(6)给出的n阶分形三角形的质量mn是以0阶的分形三角形的质量m来计算的,即mn=(3/4)nm.若第n阶分形三角形的质量为m,则最终的转动惯量应为
(7)
3 小结及教学上的启示
综上所述,通过递推的方法,仍然利用量纲分析、标度变换及平行轴定理,我们推导出了第n阶分形三角形绕通过其质心O且垂直于分形三角形平面的转轴的转动惯量 ,克服了文献[5]中无穷阶分形物体质量趋于0的问题.本文的方法可以推广到求诸如门格海绵、谢尔宾斯四面体等分形物体.
从课堂教学方面来说,文献[5]推广量纲分析法求分形物理的转动惯量是非常好的想法,特别适合于教师在大学物理的力学课堂上尝试,其一是可以让学生用物理学家的思维来思考问题,避免繁琐的数学积分,培养锻炼学生的直觉思维和科学素养;其二是通过此问题可以让一年级的学生接触分形和分数维这样一个奇妙的领域,提高学习物理的兴趣.由于分形与混沌紧密相连,而混沌又可在力学课程中讲到二体问题、三体问题时有所涉及,因而又会牵涉到一段有趣的物理学发展史,可以讨论蝴蝶效应,讨论确定性动力学系统的内禀不确定性,如此环环相扣,不断引领学生走向新的科学领域,这也应是优秀教师所需完成的教学任务之一.
[1]RobertRabinoff.Momentsofinertiabyscalingarguments:howtoavoidmessyintegrals[J].AmJPhys, 1985, 53(5):501-502.
[2]RobertRabinoff,俞志毅. 用标度变换求转动惯量: 如何避免繁杂的积分[J]. 大学物理,1987,6 (7) : 31-32.
[3]吴文旺. 用量纲分析法求解转动惯量[J]. 石家庄铁道学院学报,1993,6(3),85-90.
[4]杨忠. 用量纲分析法求平面物体的转动惯量[J]. 大学物理,1997,16 ( 4) : 45-46.
[5]许佳敏,邱为钢. 分形物体转动惯量的计算[J]. 大学物理,2011,30 ( 11) : 53-55.
Revisitonthedimensionanalysistocalculatethemomentofinertiaoffractalbody
FANGWei1,2,TUHong1,2,FENGJie1
(1.DepartmentofPhysics,ShanghaiNormalUniversity,Shanghai200234,China;2.ShanghaiKeyLabforAstrophysics,Shanghai200234,China)
Thedifferencebetweenidealinfinite-orderfractalinmathematicalsenseandrealfinite-orderfractalinphysicalsenseisdistinguished.Usingscaletransformationanddimensionanalysis,therecurrenceformulaforthemomentofinertiaofn-orderfractaltriangleisobtained,whichleadstothefinalexpressionforthemomentofinertia.Whenntendstoinfinity,theresultofthisexpressionisinaccordancewithinfinite-orderfractalobjects.
dimensionanalysis;fractal;momentofinertia;recurrence
2015-01-23:
2015-12-30
方伟(1981—),男,安徽桐城人,上海师范大学数理学院物理系副教授,博士,主要从事宇宙学暗能量方面的理论研究及与大学物理相关的教学、研究工作.
教学讨论
O303;O411
A
1000- 0712(2016)08- 0018- 04

