双侧电驱动履带车辆等效条件积分滑模稳定转向控制
曾庆含,马晓军,廖自力,魏曙光
(1.装甲兵工程学院全电化技术重点实验室,北京100072;2.装甲兵工程学院控制工程系,北京100072)
双侧电驱动履带车辆等效条件积分滑模稳定转向控制
曾庆含1,2,马晓军1,2,廖自力1,2,魏曙光1,2
(1.装甲兵工程学院全电化技术重点实验室,北京100072;2.装甲兵工程学院控制工程系,北京100072)
履带车辆转向阻力随行驶状态呈现非线性、大范围变化的现象,且由于车辆惯性大、电机驱动能力有限,易进入深度饱和状态,而双侧电机动力相互独立,要实现车辆全速度范围的稳定转向必须对两侧力矩进行有效控制。针对以上问题,设计了一种横摆角速度控制律。开展转向动力学分析,提出速度、横摆角速度转向控制结构;设计了一种带等效控制项的条件积分滑模控制算法,通过引入等效控制项,提高系统响应速度,减小滑模抖振;通过引入条件积分控制项,使滑模控制项边界层外与经典滑模性能一致,鲁棒性强,边界层内平滑切换为Anti-Windup结构的PI控制,便于消除误差,抑制积分饱和。Matlab与RecurDyn联合仿真表明,提出的算法具备跟踪能力强、抗扰动和饱和、输出控制量平滑的优点,能够实现车辆稳定转向控制。
兵器科学与技术;履带车辆;电传动;转向控制;滑模控制
0 引言
双侧电驱动结构简单、控制方便,在履带车辆中被广泛采用,美国M113、瑞典SEP以及北京理工大学的电驱动履带样车均采用该结构[1-3]。该方案中两侧驱动系统输出动力相对独立,要精确、稳定地转向,需要对其进行闭环反馈控制,协调控制两侧输出动力。履带车辆完全依靠两侧履带速度差实现“滑动转向”,不同车速、转向半径下目标横摆角速度数值变化范围宽,行驶阻力受行驶状态变化、路面参数等因素影响呈现非线性、不确定动态变化,加上车辆惯性大、电机驱动能力有限,极易进入深度饱和状态[4]。因此转向控制对算法的跟踪能力、抗扰性能、抗饱和要求较高,具有较大难度。
目前,国内外针对车辆转向运动控制算法进行了大量研究,逐渐由一般的PI控制向模糊、神经网络智能控制,向自适应、滑模变结构控制等高抗扰控制算法深入,其本质上就是提高双侧电驱动履带车辆转向的控制品质。文献[5]采用神经网络PID控制方法,通过神经网络对电机阻力矩的在线辨识、训练,实现车辆转向。文献[6-7]采用模型参考自适应、线性自抗扰的控制方法,实现了差速转向控制。文献[8]提出一种非线性积分滑模面的自适应滑模控制方法用于低速农机转向控制。文献[9-10]针对M113无人驾驶履带车辆运动控制,将其视为一对双输入双输出系统,设计了定量反馈鲁棒控制算法,抑制速度对转向通道的干扰。文献[11]以零差速电传动履带车辆为对象,设计了转向负载自适应控制策略,以适应路面不平度变化,获得期望的转向角速度响应。文献[12]以双电机耦合电传动履带车辆为对象,设计了一种解耦的速度-横摆角速度控制结构,研究了滑模控制算法,实现了解耦条件下的稳定转向控制。
上述研究大大推进了电驱动履带车辆转向控制技术的发展,但从算法验证的角度,北京理工大学进行了水平良好路面下低速转向工况的算法实车试验验证,其余大多基于Matlab构建的理想数学模型进行分析,算法实现对模型依赖强。要实现全速度范围的稳定转向,还需要继续对控制算法进行深入研究。积分滑模控制(ISMC)算法集合了滑模控制抗扰能力强和积分控制无静差跟踪的优点,同时输出抖振量小,但是存在小误差响应速度慢且容易进入深度饱和的缺点。文献[13]提出设计一种针对非线性最小相位系统的条件积分滑模控制算法,文献[14]将其应用于电动车辆牵引力控制中,取得了较好的防饱和控制效果。
本文在上述研究基础上基于“等效控制思想”,增加前馈补偿项,设计等效条件积分滑模控制(ECISMC)算法用于车辆转向横摆角速度控制,具有跟踪范围宽、精度高,抗扰能力强的优点,能够克服高速转向时离心力、电机饱和非线性影响以及低速转向时不平路面扰动的难题,实现全速度范围的稳定转向。最后,采用Matlab和RecurDyn软件,对控制算法进行联合仿真验证。
1 系统描述
双侧电驱动履带车辆结构如图1所示。发动机-发电机组输出高压直流电,作为主动力源,超级电容、动力电池并联在直流母线上作为辅助动力源,驾驶员操控信号输入给车载运动控制器,结合反馈的状态信号调节驱动电机输出转矩,进行两侧牵引力的协调控制,实现车辆正常的直线、转向行驶[14]。

图1 双侧电传动履带车辆结构图Fig.1 Structure of dual-motor electric drive tracked vehicle
履带车辆运动可以视为刚体的平面运动,将车辆的运动分解为沿行驶方向的平移和绕中心的旋转,其中直线行驶作为转向半径为无穷大时的特殊转向工况,其受地面牵引力和阻力的共同作用。由于履带车辆转向行驶动力学复杂,为便于分析,忽略转向过程中履带与地面的滑移和滑转,以向右转向为例,理想情况下动力学关系如图2所示。

图2 动力学示意图Fig.2 Schematic diagram of dynamics
图2中,B为履带中心距,L为履带接地长,Rc为车辆转向半径,ωc为转向角速度,vc为车辆中心运动速度,F1、F2分别为外、内侧牵引力,Ff为车辆滚动行驶阻力,λ为车辆转向纵向位移,Mμ为车辆转向横向阻力力矩。
车辆所受作用力、力矩数学表达式为

式中:m为车辆质量;θ为路面纵向倾角;f为路面滚动阻力系数;CD为风阻系数;A为迎风面积;Fw为迎风阻力;Fθ为坡道阻力;ρ为相对转向半径;δ为质量增加系数;T1、T2为电机输出转矩;i为传动比;r为主动轮半径;Md为不确定性横向阻力力矩,主要出现在高速、坡道等存在纵向偏移的行驶工况,包括高速转向离心力等[14];μ为路面转向阻力系数;μmax为最大转向阻力系数。
根据(1)式履带车辆动力学分析,可得动力学方程为

式中:J为车辆转动惯量。
计算可得两侧电机期望输出力矩为

通过(3)式可以明显看出,车辆转向行驶过程中电机负载力矩存在较大差异,且随路面条件、车辆运动状态大范围变化。
由于驱动电机动态响应速度远高于车辆动力学响应速度,算法设计过程中可以忽略其内部复杂电磁作用时间,重点关注电机机械输入输出能力。其数学模型可采用电机转速-转矩特性曲线进行幅值约束,并采用1阶惯性环节拟合电机动态响应时间的方法进行分析为

式中:T*为目标转矩;Tdrive(ω)、Tbrake(ω)分别为当前电机转速ω下最大驱动、制动转矩;Te为电机实际输出电磁转矩;τe为电机动态响应时间。由于电机输出能力随转速非线性变化,相当于控制系统引入1阶非线性饱和环节,对算法抗饱和能力提出了要求。
2 转向控制算法研究
根据(2)式可知,车辆行驶时刻通过调节电机输出力矩和T1+T2实现对车速vc的调节;通过调节力矩差T1-T2实现横摆角速度ωc的控制。要想实现车辆状态vc、ωc的有效控制,需要设计相应的闭环控制算法,精确计算电机期望力矩。而由(1)式可知,相比纵向车速,车辆转向阻力系数μmax随车辆速度、横摆角速度以及路面参数等呈现非线性、不确定变化,控制难度更大,需要重点针对控制算法展开研究。因此设计图3所示的履带车辆转向控制结构,采用PI控制车速,采用ECISMC控制横摆角速度。
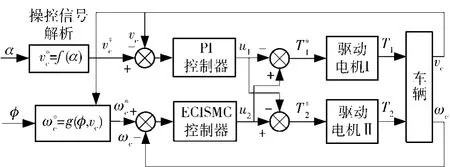
图3 控制结构框图Fig.3 Block diagram of control structure
号和车辆状态,解析制定各子系统期望信号。
行驶速度由加速踏板给定,解析函数为

横摆角速度由方向盘给定,解析函数为
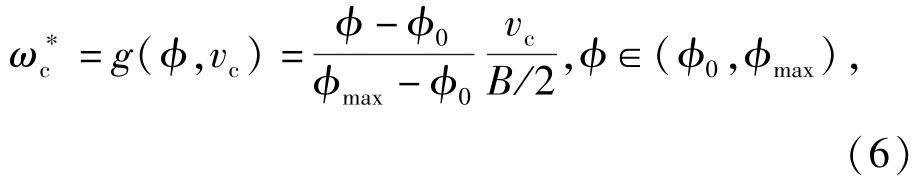
式中:φ为方向盘转角行程;φmax为最大有效行程,取95°;φ0为最小有效行程,取5°.
值得说明的是,要保证车辆转向稳定性,防止侧滑和甩尾,转向时应对最大横摆角速度作出限制。

2.1控制律设计
针对传统滑模控制算法存在的问题,设计了等效条件积分滑模的控制算法,从两方面进行了改进:一是基于“等效控制”思想,增加等效控制项,提高系统响应速度,降低切换控制项增益;二是滑模切换控制项,采用条件积分设计,边界层外采用滑模控制,边界层内过渡为Anti-windup的PI控制,兼顾滑模控制的强鲁棒性和Anti-windup的PI防饱和跟踪性能,实现横摆角速度的精确跟踪控制,避免了单纯积分滑模容易出现积分饱和、响应速度慢的问题,算法结构图4所示。按照以下步骤设计:
步骤1:在传统滑模面的基础上增加条件积分项,即
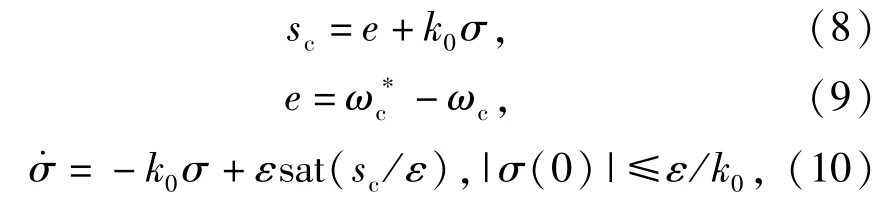
式中:φ为路面附着系数。
式中:sc(e,σ)=0是新增加的滑模面,σ∈Ωσ为积分值,e∈Ωe为给定量和反馈量的误差值;k0>0为调节参数;ε>0为滑模切换边界层宽度[13]。
步骤2:用连续趋近律sat(sc/ε)代替经典的不连续滑模控制律sign(sc/ε),即

图4 条件积分滑模控制算法结构框图Fig.4 Block diagram of sliding mode control algorithm with conditional integrator
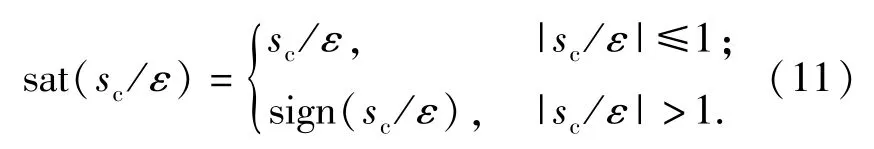
一般情况下,当符号函数sign(sc/ε)由饱和函数sat(sc/ε)逼近时,调节误差毕竟是有界的,其边界常数为k0ε,但由于存在积分作用,稳态误差可达到0.
步骤3:增加等效控制项ueq,控制律设计为

式中:β(ωc)=ρ(ωc)+β0,β0>0为一固定常数,ρ(ωc)为ωc不确定性上界;Td为滑模控制项增益;ueq为等效控制项。
根据(1)式可设

式中:^μ为转向阻力系数标称数值,^μmax为其最大值,取最大转向阻力系数数值的一半。
步骤4:假设Td取当前转速下车辆驱动电机输出力矩的最大差值,即

考虑到正常转向行驶时,阻力矩Mμ一般满足



首先分析Ωσ={|σ|≤ε/k0}为正不变子集,令Lyapunov函数为

由|σ(0)|≤ε/k0,知恒成立,σ始终收敛于Ωσ内。
控制器其滑动区域如图5所示,可分为区域Ωε={|s(e,σ)|≤ε,|σ|≤ε/k0},Ω={|s(e,σ)|>ε,|σ|≤ε/k0}两部分,下面分区域对算法控制性能进行讨论。

图5 正不变子集区域Fig.5 District of positive invariant subset
1)由于ε>0,在Ω区域内满足
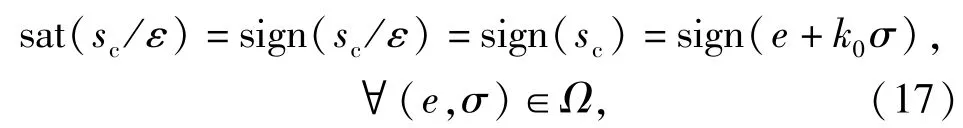
可以将Ω分为两个子集Ω=Ω+∪Ω-,Ω+为sc>0,Ω-为sc<0(由于ε>0,在区域Ωε内sc≠0)。
在Ω+区域内,有sc=e+k0σ>0,产生子集

显然有|e+k0σ|=e+k0σ,能够确定

因此e>0,在Ω+区域sign(e+k0σ)=sign(e)=1.
在Ω-区域内,e+k0σ<0,
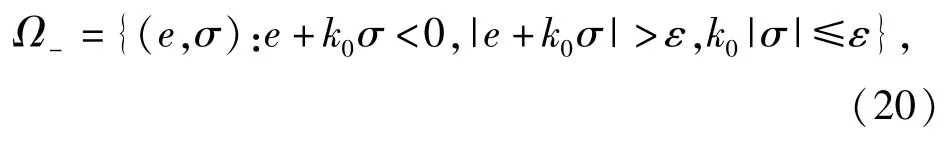
在Ω+区域内sign(e+k0σ)=sign(e)=-1.
综合区域Ω+、Ω-可以证明sat(sc/ε)= sign(e),可知对任意(e,σ)∈Ω,控制律为

在非连续滑模控制律基础上增加等效控制项ueq.
2)Ωε区域内,当系统进入Ωε,σ变成简单的误差积分项

控制律如下:

由于等效控制项ueq数值是固定的,区域Ωε内控制量由类似于PI控制对反馈补偿量进行调节产生。因此,当系统进入区域Ωε,控制器变为包含积分作用的线性控制律,而在区域Ω,仍然采用滑模控制的不连续控制律。
2.2稳定性分析
稳定性分析主要证明系统在有限时间内收敛至Ωε区域。由于Ωε∈De×Dσ,上面已证明Ωσ正不变性,主要证明在∀(e,σ)∈Ω内Ωe的正不变性。
设Lyapunov函数:V1=1/2e2,得

由动力学分析中(2)式可知

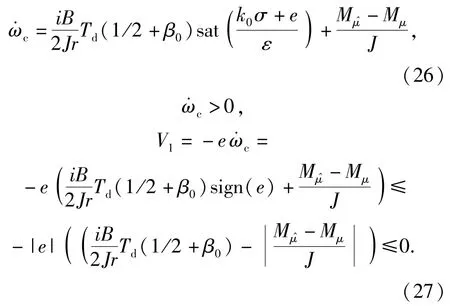
3 Matlab与RecurDyn联合仿真实验
3.1系统建模
为了验证转向控制算法的性能,本文在Simulink中构建了驾驶员操控系统、控制器、电机驱动系统的数学模型,在多体动力学仿真软件RecurDyn中建立了车辆动力学模型,通过软件接口技术进行数据交互,实现机械、电气、控制系统的一体化联合仿真[7]。
车辆动力学模型包含车体、炮塔、行动装置三部分,其中利用RecurDyn的TrackHM模块中建立车辆行动装置模型,采用主动轮前置、双销式履带、双轮缘负重轮、扭杆式独立悬挂结构。如图6所示。

图6 电传动履带车辆动力学仿真模型Fig.6 Dynamic simulation model of electric drive tracked vehicle
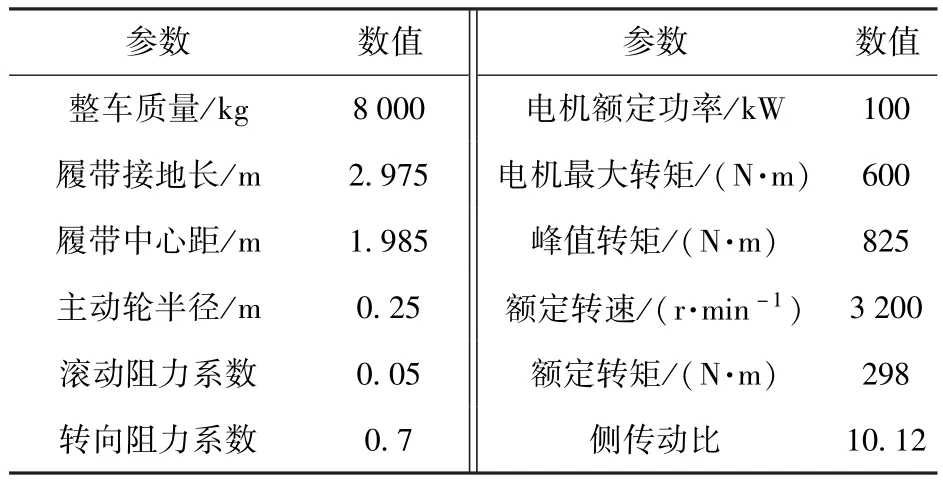
表1 车辆仿真基本参数Tab.1 Parameters of vehicle
3.2算法控制性能仿真
3.2.1不平路面低速转向稳定控制仿真分析
为了验证控制算法对不平路面低速转向稳定控制能力,进行了不平路面的转向稳定性控制仿真实验。1s时加速踏板踩至9.3°,车辆加速至10km/h并保持匀速行驶。4s时开始方向盘转角打至14°, 16s时回正,进行5B半径转向,其中5.4s由水平路面进入IV级不平路面,15s进入水平路面。

图7 IV级不平路面转向工况Fig.7 Steer on IV road
两种算法控制下的横摆角速度跟踪曲线,如图7(a)、图7(b)所示,水平路面条件下两种算法均能实现横摆角速度的精确跟踪,但进入不平度路面后,转向阻力系数随路面不平度随机变化,形成持续性的路面扰动,控制品质大大降低。对比分析输出转矩曲线图7(c)、图7(d)发现,ECISMC算法两侧转矩能够迅速响应,抑制扰动影响,其跟踪精度要优于ISMC算法,不平路面转向过程中横摆角速度反馈量最大波动范围约为后者的30%,车辆低速转向行驶稳定性明显较高。
3.2.2水平路面高速转向稳定控制仿真分析
电机转速随车速逐渐升高时,电机输出转矩能力逐渐下降,因此高速转向时极有可能出现电机转矩饱和现象,且离心力作用明显,引起路面负载呈强非线性变化,对横摆角速度控制算法抗饱和、抗扰能力要求较高。为此进行了50km/h速度下大半径修正转向仿真实验。1s时踏板踩至35°,加速至50km/h.13s时方向盘转角打至6°,进行45B大半径修正转向,16s回正,恢复至直线行驶状态。
仿真结果如图8所示,图8(a)为行驶速度曲线,图8(b)为横摆角速度曲线,图8(c)、图8(d)为两种控制算法下的两侧驱动电机输出转矩曲线。由图8可知,转向过程中电机输出处于饱和状态,基于确保车辆行驶轨迹稳定的安全性考虑,优先满足横摆力矩需求以跟踪目标横摆角速度,纵向力矩出现不足,车速有所下降,目标横摆角速度随之变化。ISMC算法控制时,系统饱和现象严重,系统转向、回正响应速度明显较慢,彻底回正时间需要2s左右,最大超调量达0.06rad/s,且不断增大,有失稳趋势,转向稳定性、操控灵活性较差。而采用本文ECISMC算法则能够克服饱和、非线性扰动等影响,系统响应速度明显加快,转向、回正响应速度分别提高0.3s、1.8s,超调量控制在0.015rad/s以内,能够精确跟踪变化的横摆角速度,实现降速平稳转向。
4 结论
1)设计了一种带等效控制项的条件积分滑模控制算法,通过引入等效控制项,提高系统响应速度,减小滑模抖振;通过引入条件积分控制项,使滑模控制项边界层外与经典滑模性能一致,响应快、鲁棒性强,边界层内平滑切换为Anti-Windup结构的PI控制,便于消除跟踪误差,防止积分饱和。
2)设计的横摆角速度控制算法,跟踪能力、抗扰能力强,能够克服路面转向阻力随机扰动、非线性变化和电机饱和的影响,降低控制输出量抖振,实现车辆多转向工况下的横摆角速度的精确跟踪,与ISMC算法相比,低速不平路面转向跟踪波动范围降低约70%,高速转向超调量降低约75%,转向、回正响应速度分别提高约0.3s、1.8s,提高了全速度范围内车辆转向的稳定控制性能。

图8 50km/h转向仿真曲线Fig.8 Steer at 50 km/h
(References)
[1] Savage S.Electric/hybrid electric drive vehicles for military applications promises and chanllenges[J].Military Technology,2007(9):132-144.
[2] Brudnak M,Shvartsman A,Pozolo M,et al.Virtual combat vehicle experimentation for duty cycle measurement[J].SAE International Journal of Commercial Vehicles,2008,1(1):54-70.
[3] 曾望.国外装甲车辆全电技术的最新发展[J].现代军事,2010(12):52-58. ZENG Wang.Latest development of armored vehicles electrical technology abroad[J].Modern Military,2010(12):52-58.(in Chinese)
[4] 周宏,谭文.线性自抗扰控制的抗饱和补偿措施[J].控制理论与应用,2014,31(11):1457-1463. ZHOU Hong,TAN Wen.Anti-windup schemes for linear active disturbance rejection control[J].Control Theory and Applications,2014,31(11):1457-1463.(in Chinese)
[5] 翟丽,孙逢春,谷中丽.电子差速履带车辆转向转矩神经网络PID控制[J].农业机械学报,2009,40(2):1-5. ZHAI Li,SUN Feng-chun,GU Zhong-li.Neural networks PID control of steering torque for electronic differential tracked vehicle[J].Transaction of Chinese Society for Agricultural Machinery,2009,40(2):1-5.(in Chinese)
[6] 翟丽,孙逢春,谷中丽.电传动履带车辆电子差速转向控制策略[J].北京理工大学学报,2009,29(2):113-117. ZHAI Li,SUN Feng-chun,GU Zhong-li,et al.Steering control strategy of electronic differential speed in electric drive tracked vehicle[J].Transactions of Beijing Institute of Technology,2009,29(2):113-117.(in Chinese)
[7] 马晓军,曾庆含.采用线性自抗扰的电传动履带车辆电子差速控制[J].兵工学报,2014,35(12):1944-1950. MA Xiao-jun,ZENG Qing-han.Electric differential of electric drive tracked vehicle with linear active disturbance rejection control[J].Acta Armamentarii,2014,35(12):1944-1950.(in Chinese)
[8] Li T,Hu J.Adaptive sliding mode control method based on nonlinear integral sliding surface for agricultural vehicle steering control[J].Mathematical Problems in Engineering,2014,30(4): 257-325.
[9] Wang G G,Wang S H,Chen C W.Design of turning control of tracked vehicle[J].IEEE Control System Magazine,1990,17(2):122-125.
[10] Wang G G,Horowitz I,Wang S H,et al.A control design for a tracked vehicle with implicit nonlinearities using quantitative feedback theory[C]∥Proceedings of the 28th IEEE Conference of Decision and Control.Tampa,Florida:IEEE,1988:2416-2418.
[11] 刘翼,毛明,马晓枫,等.零差速电传动履带车辆转向负载自适应控制策略研究[J].车辆与动力技术,2013(1):7-11. LIU Yi,MAO Ming,MA Xiao-feng,et al.Research on self-adaptive steering control strategy for single motor cross drive electric transmission for tracked vehicles[J].Vehicle and Power Technology,2013(1):7-11.(in Chinese)
[12] 盖江涛,黄守道,周广明,等.双电机耦合驱动履带车辆自适应滑模转向控制[J],兵工学报,2015,36(3):405-411. GAI Jiang-tao,HUANG Shou-dao,ZHOU Guang-ming,et al.A-daptive sliding mode steering control of double motor coupling drive transmission for tracked vehicle[J].Acta Armamentarii,2015,36(3):405-411.(in Chinese)
[13] De Castro R,Araujo R E,Freitas D.Wheel slip control of EVs based on sliding mode technique with conditional integrators[J]. IEEE Transactions on Industrial Electronics,2013,60(8): 3256-3271.
[14] Seshagiri S,Khalil H K.Robust output feedback regulation of minimum-phase nonlinear systems using conditional integrators[J].Automatica,2005,41(1):43-54.
Stable Steer Control of Electric Drive Tracked Vehicle Based on Equivalent Sliding Mode Technique with Conditional Integrator
ZENG Qing-han1,2,MA Xiao-jun1,2,LIAO Zi-li1,2,WEI Shu-guang1,2
(1.Laboratory of All-electrization Technology,Academy of Armored Force Engineering,Beijing 100072,China;2.Department of Control Engineering,Academy of Armored Force Engineering,Beijing 100072,China)
The steer resistance of tracked vehicle has character of nonlinear and wide range change,and the drive system is very likely to be saturated dual to large vehicle inertia and constrained drive torque,while the drive motors of dual-motor tracked vehicle are independent with each other,which leads to regulate the drive torque per side to realize stable steer.In order to improve the stability of steer,the sliding mode technique with conditional integrator is applied to yaw rate control.A velocity-yaw rate steer control structure is developed through dynamics analysis.The equivalent conditional integral sliding mode control(ECISMC)algorithm is designed,which could increase the response speed through equivalent term feedforward compensation and adopt the robust and rapid discontinuous nature of the sliding control outside boundary layer,enabling smooth transition to a PI control law with anti-windup inside boundary layer to eliminate track error by the conditional integrator approach.Co-simulation of Matlab and RecurDyn shows that the control algorithm has advantages of high precision,robust to disturbance,anti-windup andsmooth control input,which could realize stable steer performance.
ordnance science and technology;tracked vehicle;electric drive;steer control;sliding mode control
TJ81+0.323
A
1000-1093(2016)08-1351-08
10.3969/j.issn.1000-1093.2016.08.002
2015-11-26
军队院校科技创新项目(12050005)
曾庆含(1988—),男,博士研究生。E-mail:cqh_zgy@163.com;马晓军(1963—),男,教授,博士生导师。E-mail:maxiaojun_zgy@163.com

