基于等效力方法的双旋弹侧向控制力落点响应分析
王钰,王晓鸣,程杰,于纪言
(南京理工大学智能弹药技术国防重点学科实验室,江苏南京210094)
基于等效力方法的双旋弹侧向控制力落点响应分析
王钰,王晓鸣,程杰,于纪言
(南京理工大学智能弹药技术国防重点学科实验室,江苏南京210094)
为研究双旋式弹道修正弹在侧向控制力作用下弹丸的落点响应规律,实现控制力作用下落点修正量的简便计算,提出等效控制力方法。将侧向控制力对弹丸质心运动的影响分解为力的直接作用和力与力矩引起的角运动变化产生的间接影响。基于双旋弹的7自由度弹道模型,推导出受控条件下弹丸平均攻角的变化量,从而求解等效控制力,并依此推导出控制力引起的落点位置变化量的理论表达式。理论分析表明,其余参数相同时,修正距离与控制力作用点到质心的距离几乎呈正比。仿真和实验数据表明,理论公式计算的误差在10%以内。
兵器科学与技术;双旋弹;侧向控制力;落点修正量;提前相位角
0 引言
无控弹药的灵巧化和制导化是当今弹药技术发展的趋势和主流方向之一,弹道修正弹作为其中一员,越来越得到国内外科学家的重视。弹道修正弹采用弹道修正技术,完成弹丸的简易弹道修正功能,使其能够在预定目标起爆,具有精度较高、低成本、高作战效能的特点。在施加了修正力之后,弹丸姿态和落点的变化情况,对于修正弹丸修正能力和控制方法的研究有至关重要的影响。
1995年Grosso[1]在美国专利中提出了灵巧弹药的隔转空气鸭舵控制概念,提到对于旋转稳定弹丸向左的侧向力会带来弹丸平均攻角向右偏的效果。Corriveau等[2]以PRODAS软件为工具对105mm旋转稳定弹丸进行了大量的6自由度弹道模型仿真发现,左舷的的侧向力使得弹丸落点右偏,右舷的侧向力使得落点左偏,这种修正效果与尾翼稳定弹丸相反。文献[3-5]则从线性化理论出发简化6自由度刚体修正弹道,明确给出了角运动响应幅值与相位偏差的分析公式,仿真结果也显示侧向力修正响应结果与力作用点和质心、压心位置密切相关,并且给出了旋转稳定弹丸角运动对侧向力响应存在180°偏差的物理解释。Fresconi等[6]以完整7自由度模型进行了大量的数值仿真,给出了修正力幅值、力作用点、滚转控制对弹丸落点攻角变化的影响。国内,常思江等[7]对鸭式布局的双旋弹丸进行了动力学建模,并通过仿真分析对控制力和力矩作用下的双旋弹丸攻角响应进行了分析。许诺等[8]经过模型简化,得到双旋弹丸角运动方程,并得到当鸭舵转角固定时,弹体可以获得与鸭舵安装角近似呈正比的弹道修正能力。张蛟龙[9]通过仿真研究了不同起控时间的修正能力。朱大林[10]采用弹丸线性化理论和Murphy的复变量方法建立弹丸复攻角运动方程,并进行了稳定性分析。Gao等[11]对于侧向力对旋转稳定弹丸的修正效果也进行了有效地建模和分析。国内外学者对控制力作用下弹丸的瞬态响应均开展了定性或定量的建模和分析。但对控制力作用下弹丸落点响应的定量分析还没有得到足够的重视,相关研究较少,难以支撑双旋弹丸的控制策略研究。为解决该问题,本文采用基于等效力分析的方法,推导了控制力作用下弹丸的落点响应方程,在考虑不同弹丸参数条件下,分析了控制力作用下的弹丸位置变化和落点响应情况。
1 控制力引起的角运动
对于双旋弹丸,由于控制力作用点不在弹丸质心,在控制阶段,控制力对弹丸质心运动产生影响,其相对于质心的力矩也对弹丸的角运动产生影响。为分析控制力对弹丸角运动的影响,首先建立双旋弹丸的7自由度弹道模型,然后推导出侧向控制力作用下的弹丸角运动方程。
1.1弹道模型建立
本文研究的双旋弹丸模型如图1所示,其中pA、pF分别表示弹丸尾部和头部的滚转角速度,φA、φF分别表示弹丸尾部和头部的滚转角,lCG表示侧向控制力作用点与全弹质心在弹轴方向上的距离。

图1 双旋模型Fig.1 Dual-spin model of projectile
在小攻角范围内,阻力受鸭舵相位角的影响可忽略不计[12],故可将鸭舵引起的诱导阻力作为弹体固定的气动力,从而忽略鸭舵所受控制力在弹轴方向的分量,则弹丸侧向控制力在弹轴系下的分量可记为Fc=[0FcηFcζ].文中使用的基准、弹轴和弹道坐标系定义见参考文献[13]。
在弹道坐标系下建立弹道方程的运动学模型,在弹轴坐标系下建立动力学模型,则有控双旋弹丸的7自由度模型,如(1)式~(4)式所示:

式中:m为全弹质量;v表示弹丸速度;θv、ψv表示速度高低角、速度方位角;x、y、z表示基准坐标系下的弹丸位置;θa、ψa表示弹轴高低角、弹轴方位角;Fxv、Fyv、Fzv表示弹道坐标系Ovxvyvzv下弹体总体所受合力在xv、yv及zv轴上的投影,包括气动力和重力的合力F0及舵翼受到的控制力Fc两部分;MεA、MεF分别表示弹轴坐标系下弹丸尾部和头部所受力矩在ε轴上的投影;Mη、Mζ表示弹丸总体所受合力矩在η、ζ轴上的投影,包括总气动力矩M0和控制力矩Mc两个部分,Mη=MηA+MηF,Mζ=MεA+MεF;q、r分别表示俯仰和偏航角速度;IxA、IxF和IyA、IyF分别表示弹尾和弹头部分在x轴和y轴方向的转动惯量,且满足Iy=IyA+IyF;H*=pAIxA+pFIxF.
经过坐标转换,侧向控制力在弹道系下的投影和控制力矩在弹轴系下的投影为

式中:Fcη、Fcζ、Fcxv、Fcyv、Fczv分别表示控制力在弹轴系和弹道系各坐标轴下的分量;δv和δh分别为高低和水平攻角;Mcε表示舵翼所受ε方向上的导转力矩;Mcη、Mcζ分别为η和ζ方向上的控制力矩分量。对于双旋弹丸,舵翼所受总的侧向控制力记为f,控制相位角为φF,则有Fc=Fcη+iFcζ=feiφF.定义在弹尾向弹头视图中,控制力向上时控制相位角φF= 0°,向右时φF=90°,如图2所示。
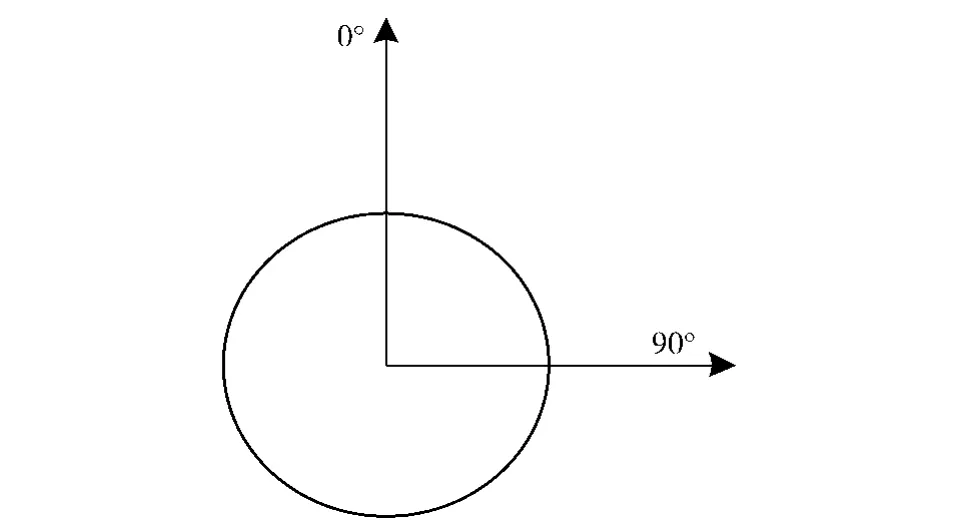
图2 控制相位角定义(弹尾向弹头视图)Fig.2 Definition of control force direction(from projectile tail to head)
1.2控制力作用下的攻角方程
对于双旋弹道修正弹,假设弹丸在控制阶段与无控阶段均能保持旋转稳定,则侧向控制力对弹丸角运动的影响可作为扰动分析。引入只考虑阻力和重力的理想弹道模型,此时弹道倾角表示为θi.基于上述假设,可将理想弹道中未考虑的其他因素视作扰动,可得7自由度弹道模型中速度高低角θv= θi+ψ1,弹轴高低角θa=θi+φ1,ψ1为有控弹道速度高低角和理想弹道倾角的差值,φ1为有控弹道弹轴高低角和理想弹道倾角的差值。
与理想弹道模型不同,高速旋转弹丸在实际飞行过程中弹轴与速度轴不重合,相对于理想弹道模型,使用复摆动角Φ=φ1+iψa表示的弹轴的空间方位,复偏角Ψ=ψ1+iψv表示相速度方向[13]。攻角定义为弹轴与速度轴的夹角,故有Δ=Φ-Ψ= δv+iδh.综合上述分析与假设,则φ1、ψa、ψ1、ψv、δv、δh均为小量。
1.2.1复攻角方程
复偏角可表示为:Ψ=ψ1+iψv,i为虚数符号。将理想弹道模型代入到(1)式中,并略去高阶小量,得复偏角方程:

复摆动角可表示为:Φ=φ1+iψa.将理想弹道模型代入(3)式和(4)式中,经简化可得复摆动方程:

式中:kzz=ClpρSd2/(2Iy),Clp表示滚转阻尼系数导数;kz=CMaρSd/(2Iy),CMa为翻转力矩系数导数;ky=CmpaρSd2/(2Iy),Cmpa为马格努斯力矩系数二次导数。

式中:H=by-bx-gsinθv-2+kzz;M=kz;P=(pAIxA+
pFIxF)×(Iyv)-1;T=by-Iyky(pAIxA+pFIxF)-1.
1.2.2控制力(矩)引起的攻角变化量
弹丸无控飞行阶段,弹丸舵翼自由旋转,舵翼所受的侧向力周期性地施加在弹丸头部。由于弹丸无控飞行时间远大于舵翼转动的周期,可认为舵翼提供的侧向力作用在旋转过程中相互抵消,未对弹丸的平均攻角产生明显地影响。有控制飞行阶段,控制相位角固定,对弹丸施加相对固定的侧向力。此时攻角方程(见(9)式)右侧控制力相关项会直接影响攻角方程的解,故而对弹丸平均攻角产生明显的影响。
由于弹尾部分的转动惯量远大于弹头部分,弹尾部分转速远大于弹头部分转速,又由于本文考虑的控制力(矩)不影响弹丸的稳定性,且攻角为小量,故控制力(矩)对于每一小段弹道的弹道诸元的影响均较小,可假设有控与无控状态下的H、M、P、T不变。因此,无控与有控情况下的攻角方程近似,仅右侧的控制力相关项不同,故控制力和力矩引起的平均攻角变化量可近似为只保留控制力(矩)相关项的弹丸攻角方程特解。

用系数冻结法,研究任意小段弹道,可求得由控制力(矩)产生的平均攻角为

由于公式比较复杂,不易分析,而且控制力的导数在实际使用中难以获得,故进行简化。在全弹道过程中v与其他参数相比很大,可忽略其高阶分母项;与Iykzz等项相比和项很小,可忽略;与M相比,PT值很小,也可忽略。经简化的平均攻角为
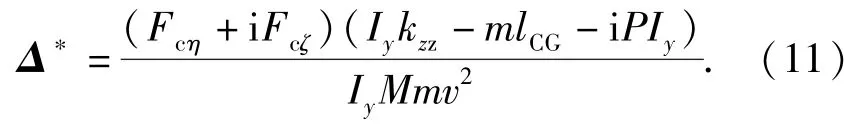
由(11)式可知:控制力对攻角的影响在方向上是耦合的,即左右方向的侧向控制力,除了使得方向攻角发生变化外,对高低攻角也有影响;高低方向同理。对于双旋弹丸,侧向控制力由弹头部的舵翼提供,则lCG>Iykzzm-1,由(11)式可知,在控制力弹轴平面,攻角的变化方向与控制力方向相反。
对105mm弹丸进行仿真计算,设定控制力为10N,飞行10s后开始控制,弹丸的相关参数如表1所示,详见参考文献[14]。控制力方向分别为0°、90°、180°、270°时弹丸飞行过程中的复攻角变化情况如图3所示。由图3可知,起控后弹丸的攻角突然产生振荡。随着飞行过程中控制力的持续作用,弹丸攻角逐渐收敛,控制力方向不同,收敛值也不相同。向上(下)施力时,主要体现为高低攻角减小(增大);向右(左)施力时,水平攻角减小(增大),与理论推导相符。
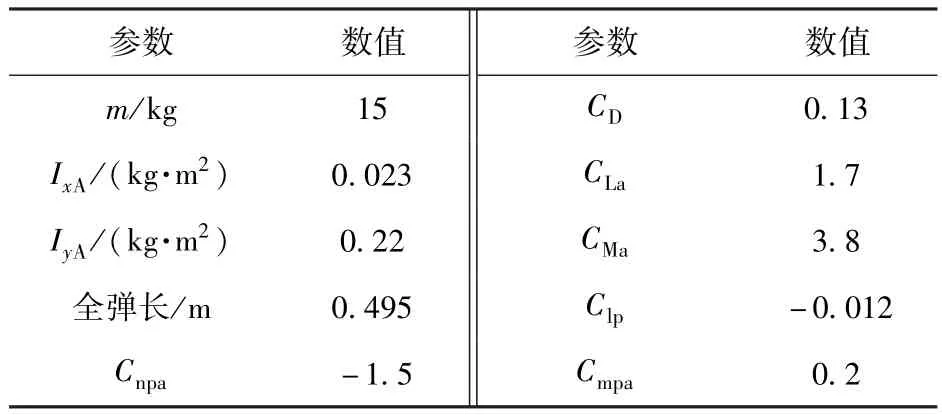
表1 105mm弹丸参数表Tab.1 Parameters of 105 mm projectile

图3 105mm弹丸不同方向控制力作用下复攻角图(lCG=0.3m)Fig.3 Complex angles of attack of a 105 mm projectile with control force in different directions(lCG=0.3m)
为进一步考查维持有控飞行、从无控到有控和从有控到无控的状态切换过程中,不同控制力方向作用下角运动变化情况下理论计算值与仿真值的贴合程度。设定飞行起控时间为10s,结束控制时间为40s,对105mm弹丸进行仿真计算,考察无控弹道与有控弹道攻角的差值,并与根据(11)式计算出的理论值比较。分别比较0°和90°控制相位角时仿真和理论计算的攻角变化量,如图4和图5所示。

图4 0°控制时与无控相比高低攻角变化量Fig.4 Comparison of theoretical and simulated angles of attack caused by control force at 0°

图5 90°控制时与无控相比水平攻角变化量Fig.5 Comparison of theoretical and simulated angles of sideslip caused by control force at 90°
由图5可知,仿真结果中起控和结束控制时,攻角的变化量均有振荡过程,然后逐渐收敛;理论计算的结果则与仿真获得的攻角变化量的均值很接近,能够表现角运动的平均变化情况。对于不同角度控制情况下,(11)式对于攻角变化量均值的计算均能较好的贴合仿真值。
2 等效控制力
由第1节的推导可知,当高旋弹丸受到侧向控制力Fc作用时,平均攻角的变化量为Δ*.根据攻角的经典理论可知,当弹丸角运动形成攻角时立刻产生在攻角平面内与速度垂直的升力和垂直于攻角平面的马格努斯力[13]。故Δ*对弹丸产生了附加的升力和马格努斯力,其综合效应即体现为控制力对角运动影响,从而产生的附加控制力Fa.这种附加控制力与控制力本身的合力即为等效控制力,控制力对弹丸质点运动的影响即为等效控制力的作用效果。
2.1角运动引起的附加控制力
由(11)式计算出的控制力产生的平均攻角Δ*是无控和有控弹道攻角之差的平均值。因此与无控弹丸相比,有控弹丸多了控制力和控制力所衍生出的附加力——Δ*产生的升力和马格努斯力。向上的平均攻角偏差量产生向上的升力和向左的马格努斯力;向右的平均攻角偏差量产生向右的升力和向上的马氏力。
这种由于平均攻角变化引起的弹丸气动力变化量记为附加控制力,速度系下的附加控制力为

2.2角运动引起的附加阻力
根据上述推导可知,有控飞行的弹丸攻角与无控飞行时相比,有较大差距。即便弹丸仍然保持飞行稳定,攻角不致过大,但其对阻力的影响不可忽略。为方便计算,考虑平均攻角变化量引起的阻力变化量作为附加阻力FD进行计算,如(13)式所示。其中阻力模型依据参考文献[12]建立,弹翼组合体阻力系数可表示为CxBW=CD0+CD2δ2,CD0为零升阻力系数,CD2为阻力系数对攻角的2阶导数,δ=
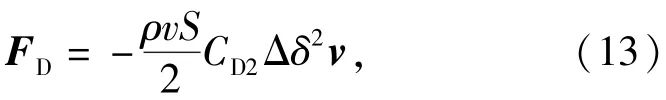
2.3等效控制力
2.3.1理论推导
控制力对弹丸落点的影响主要体现在以下两个方面:1)控制力直接对弹道轨迹的影响;2)由于控制力和控制力矩对弹丸角运动的影响间接产生对弹道轨迹的影响。因此控制力对弹丸质心运动的影响主要源于控制力Fc(见(5)式)、角运动产生的附加控制力Fa(见(12)式)和附加阻力(见(13)式)作用的叠加,则等效控制力为

将(5)式、(12)式与(13)式代入(14)式,获得等效控制力的具体表达式,适当简化并投影到弹轴系上,得弹轴系下的等效控制力表达式为

由(15)式可知,当弹丸的结构和气动参数满足1-lCGCLa/(dCMa)<0时,附加控制力对弹丸质心运动的影响占主导,故而体现为弹丸落点偏向与控制力方向相反。结合翻转力矩系数导数CMa与升力系数导数CLa的关系,定义参考参量:Pref=1-lCGh-1,其中h表示弹丸压心到质心之间的距离。当参考参量Pref为负时(lCG>h),施力点在压心之前,弹丸落点的偏向与控制力方向相反;当Pref为正时(lCG>h),施力点在压心之后,落点的偏向与控制力方向相同。且Pref绝对值与修正能力几乎呈正比。对于鸭舵式的弹道修正弹而言,控制力的施力点往往在压心之前,故而可以从理论上解释此类弹丸的控制力响应与控制力方向相反的现象,也可与Costello等[3]的研究相互验证。
2.3.2仿真验证
为验证不同参考参量情况下弹丸修正量的关系,使用155mm弹丸参数(如表2所示)进行仿真。控制力大小设定为10N,改变控制力作用点的位置,计算不同位置对应的参考参量和修正量,如图6所示。修正距离表示有控弹丸与无控弹丸之间的距离,在控制力方向,当有控弹丸落点向控制力方向移动,修正距离为正,反向为负。

表2 155mm弹丸参数Tab.2 Parameters of 155 mm projectile
由图6可知,落点修正距离几乎与参考参量呈正比,且理论值与仿真值符合得很好。当参考参量为正时,落点修正距离为正;当参考参量为负时,落点修正距离为负。即落点修正的方向与参考参量的方向相同。在相同的控制条件下,参考参量的绝对值越大,落点修正距离的绝对值越大。
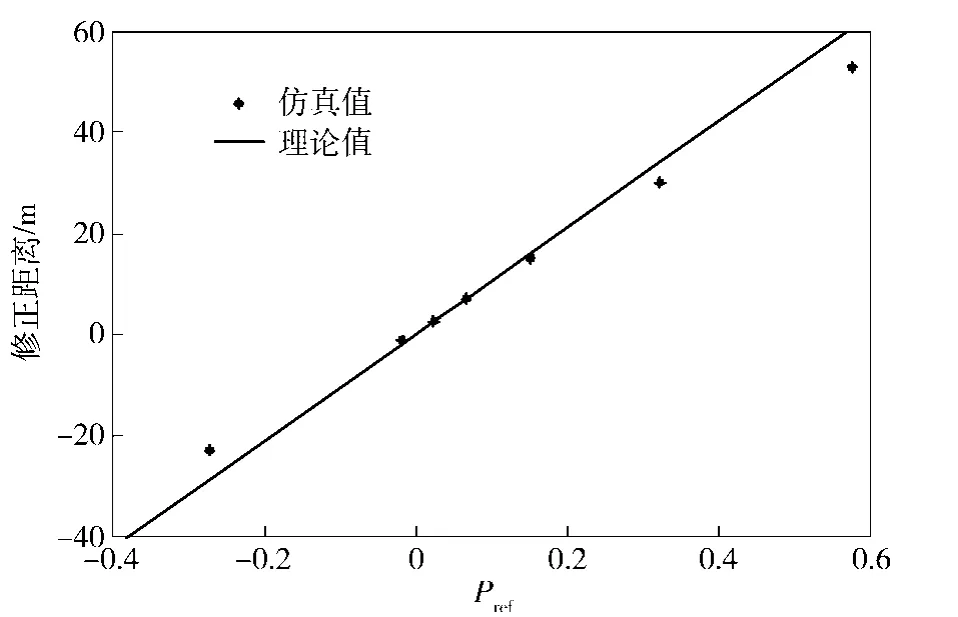
图6 参考参量与修正距离关系图Fig.6 Relation between correction quantity and reference parameter
3 修正效果预测
根据牛顿定律可以方便地计算出等效控制力(由(14)式计算获得)作用下弹丸位置的变化量,然后根据弹丸高度的变化量,计算弹丸飞行时间的变化量,从而推算出落点变化量。最后用理论计算在不同控制力作用下的落点变化量与仿真、实验数据对比。
3.1落点变化量
由于控制力作用,弹丸在飞行过程中偏离无控弹道,从而偏离无控落点。控制力对弹丸落点变化的影响主要包括:1)有控飞行段,控制力和控制力矩对弹丸质心运动的影响;2)控制结束后的自由飞行段,由于有控飞行段对弹丸速度的影响在自由飞行段的持续,对落点造成的影响。
当在弹丸飞行过程中施加控制力Fc,并维持时间tc秒,然后自由飞行tn秒,根据上述分析,有控与无控的位置变化量为

当落点高度保持一致时,由于控制力对高度方向位移的影响,有控与无控飞行时间不同。弹丸有控飞行与无控飞行之间的时间差记为Δt.由于旋转稳定式弹道修正弹中控制力对弹丸的飞行影响较小,对飞行时间的变化量也较小,故假设在Δt时间段内,有控或无控弹丸处于匀加速运动状态,且加速度近似。故有控弹道与无控弹道的时间差Δt可由(17)式计算获得,其中vy和ay分别为无控弹道y方向落点速度和加速度。

综合考虑控制力对位置和落地时间的影响,得控制力作用下落点位置的变化量(即对射程和横偏的影响)为

3.2修正效果评估
对于固定鸭舵式双旋弹丸而言,控制指令为控制相位角φF,故为方便控制指令的提出,使用修正量和提前相位角评估控制力对弹丸的修正效果。修正量Δ表示控制力施加一段时间之后,有控落点与无控落点之间的直线距离。定义落点的修正方向角与弹头部控制相位角(即控制力方向)φF之间的差值为提前相位角。其中落点的修正方向角定义为+x方向为0°,+z方向为90°;控制相位角φF的定义如图2所示。根据定义,修正量Δ和提前相位角γ的表达式为
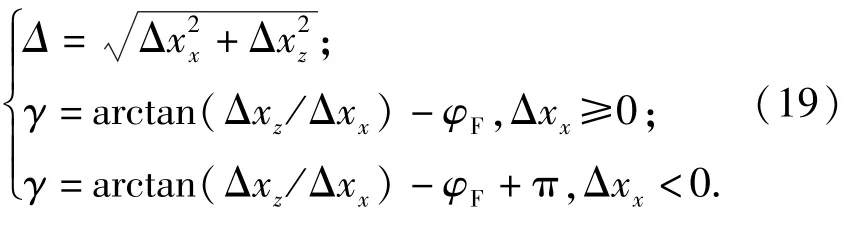
3.3仿真、实验验证
3.3.1仿真验证
为验证上述修正效果预测方法的可行性,对105mm弹丸(参数如表1所示)进行仿真计算,控制力施力点距质心0.3m.25s起控,60s结束控制,计算不同控制相位角下的有控落点,与无控落点进行比较获得仿真修正效果。
实测输入参数使用有控弹道仿真计算值代入,提前录入的先验弹道参数使用无控弹道计算值,代入(16)式计算理论时间差Δt和理论落点影响量;代入为检验使用无控弹道参数进行时间差Δt的合理性,分别使用有控参数和无控参数对Δt进行理论计算。控制力大小设定为恒定的10N时,对比理论与仿真获得的时间差如表3所示。为验证不同攻角下落点预测的精度,分别比较不同大小(10N和20N)、方向的控制力作用下的理论与仿真计算的落点偏差量如表4所示。

表3 理论与仿真时间差Δt比较表Tab.3 Comparison of theoretical and numerical Δt
由表3数据可知,使用无控数据和有控数据计算的理论Δt值非常接近,故使用无控弹道数据计算Δt可行。当Δt较小时,即主要修正横偏时,Δt的理论计算误差较大;反之,主要修正射程时,Δt的理论计算较精确。主修正方向的修正量计算比较精确,非主修正方向的计算精度较差。
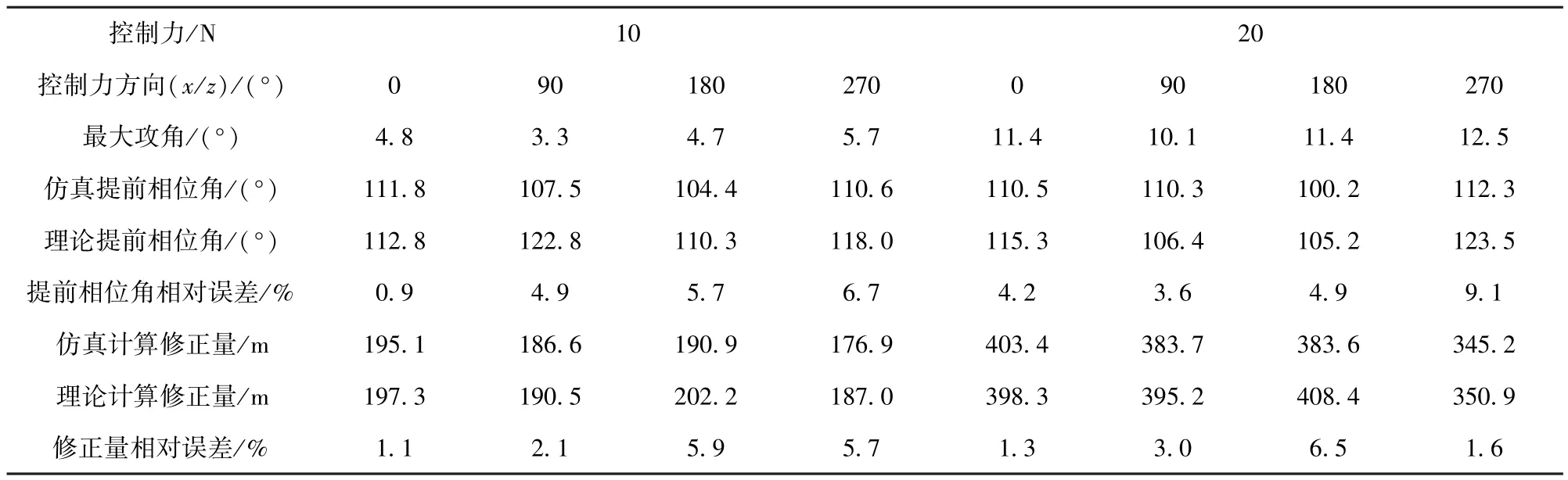
表4 理论与仿真修正效果比较表Tab.4 Comparison of theoretical and numerical correction effects
由表4可知,控制力越大,对应的弹道最大攻角越大。控制力为10N时,攻角较小(<6°),提前相位角和修正量预测相对误差均小于7%;控制力为20N时,攻角较大(>10°),提前相位角和修正量的预测相对误差略大于小攻角情况,但仍在10%以内。综上所述,不同控制条件下,理论计算的提前相位角和修正量与仿真结果相比,相对误差均在10%以内,能满足使用要求。
3.3.2实验验证
为进一步验证理论计算的正确性,使用某155mm双旋式弹道修正弹进行程控飞行实验(飞行过程中在控制阶段始终将舵翼控制在固定的角度),回收读取的弹载实测数据进行比较验证。弹体实测数据包括:卫星测得的弹丸速度和位置数据;地磁和霍尔测得的弹体和舵翼的转速和滚转角。
选取控制阶段t1、t2(t1<t2)两个时间点,分别以其对应的弹载实测速度、位置、转速等数据作为初始参数进行无控弹道预测,得到对应的预测落点D1和D2.D1表示从t1时刻开始无控飞行的弹丸落点;D2表示t1到t2时间段有控飞行,而t2时刻开始无控飞行的弹丸落点。则D1和D2之间的距离表示t1到t2时间段控制力作用对落点的影响。
为使预测和理论计算更贴近实验,预测和理论计算均使用实验当天实测的实验地气象数据。并使用同种弹丸无控飞行实验实测的弹道数据对计算使用的气动参数进行小幅度的拟合修正,并将修正后的参数用于落点预测和理论修正量计算。实验时的侧向控制力大小随马赫数等参数不断变化,使用该弹丸侧向控制力系数(方法参考文献[15])对弹丸控制力进行计算,理论计算时使用分段积分的方法对变化的控制力引起的落点变化量进行计算。理论计算均使用无控飞行弹道数据作为输入量。
进行了两发程控实验,根据弹上回读数据,一发实际控制稳定时间为80~101s,控制角度为155.0°;另一发实际控制稳定时间为70~95s,控制角度为44.8°.分别对这两发弹丸的实测数据进行计算处理,比较理论计算的提前相位角和修正量与根据实验数据预测的落点处理获得的结果,如表5所示。

表5 理论与实验修正效果比较表Tab.5 Comparison of theoretical and experimental correction effects
4 结论
本文通过建立适用于双旋弹丸的7自由度弹道模型,推导了控制力作用下的弹丸攻角方程,从而得到了高旋弹丸在侧向控制力作用下的落点修正量和提前相位角的公式。研究结论如下:
1)当参考参量Pref<0,即控制力施力点在压心之前时,落点偏向与控制力方向相反;当参考参量为正,即施力点在压心之后时,落点偏向与力的方向相同。参考参量与修正距离几乎呈正比。在弹丸参数、控制参数已知的条件下,可根据(19)式求解出弹丸落点的偏移量,从而方便地预测该段控制的作用效果。
2)当使用弹道预测方法进行弹道修正时,已知目标点与预测落点的偏差,可根据(19)式计算出该时段和控制力方向对应的提前相位角,从而为控制指令的提出提供依据。
3)经过7自由度弹道仿真和程控飞行实验验证,理论计算的提前相位角和修正量与仿真、实验结果获得的结果相比误差在10%以内。误差的主要来源有:使用攻角的均值计算整个弹丸的角运动影响,忽略了起控和结束控制阶段弹丸角运动震荡对弹丸质心运动造成的影响;理论计算时使用的先验信息均为无控弹道的相关参数,与实际有控弹道有一定差距。
本文使用的等效控制力分析方法在计算时有一定误差,但对于高旋弹丸侧向力作用下的响应情况,尤其是弹上计算提前相位角和控制后落点的变化情况有很实际的参考意义。
(References)
[1] Grosso V A.Modular aerodynamic gyrodynamic intelligent controlled projectile and method of operating same:US,5425514[P].1995-06-20.
[2] Corriveau D,Berner C,Fleck V.Trajectory correction using impulse thrusters for conventional artillery projectiles[C]∥23rd International Symposium on Ballistics Tarragona.Tarragona,Spain: IBC,2007:639-646.
[3] Costello M F,Peterson A A.Linear theory of a dual-spinning projectile in atmospheric flight[J].Journal of Guidance,Control,and Dynamics,2000,23(5):789-797.
[4] Burchett B,Peterson A,Costello M F.Prediction of swerving motion of a dual-spinning projectile with lateral pulsejets in atmospheric flight[J].Mathematical and Computer Modeling,2002,35(7/8):821-834.
[5] Ollerenshaw D,Costello M F.Simplified projectile swerve solution for general control inputs[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1259-1265.
[6] Fresconi F,Plostins P.Control mechanism strategies for spin-stabilized projectiles[J].Journal of Aerospace Engineering,2010,224(9):979-991.
[7] 常思江,王中原,刘铁铮.鸭式布局双旋弹飞行动力学建模与仿真[J].弹道学报,2014,26(3):1-6. CHANG Si-jiang,WANG Zhong-yuan,LIU Tie-zheng.Modeling and simulation of flight dynamics for dual-spin stabilized projectile equipped with canards[J].Journal of Ballistics,2014,26(3): 1-6.(in Chinese)
[8] 许诺,于剑桥,王亚飞,等.固定翼双旋弹动力学特性分析[J].兵工学报,2015,36(4):602-609. XU Nuo,YU Jian-qiao,WANG Ya-fei,et al.Analysis of dynamic characteristics of fixed-wing dual-spin projectiles[J].Acta Amarmanentarii,2015,36(4):602-609.(in Chinese)
[9] 张蛟龙.鸭式布局双旋弹飞行力学特性研究[D].南京:南京理工大学,2015. ZHANG Jiao-long.Investigation on flight dynamic characteristics of dual-spin stabilized projectiles equipped with canard[D].Nanjing:Nanjing University of Science and Technology,2015.(in Chinese)
[10] 朱大林.双旋弹飞行特性与制导控制方案研究[D].北京:北京理工大学,2015. ZHU Da-lin.Research on flight characteristics,guidance,and control for a dual-spin projectile[D].Bejing:Beijing Institute of Technology,2015.(in Chinese)
[11] Gao Y,Gu L X,Pan L.Modeling and simulating dynamics of missiles with deflectable nose control[J].Chinese Journal of Aeronautics,2009,22(5):474-479.
[12] 程杰,于纪言,王晓鸣,等.隔转鸭舵式弹道修正弹气动力工程模型与辨识[J].兵工学报,2014,35(10):1542-1548. CHENG Jie,YU Ji-yan,WANG Xiao-ming,et al.Engineering modeling and identification of aerodynamics of trajectory correction projectile with decoupled canard[J].Acta Armamentarii,2014,35(10):1542-1548.(in Chinese)
[13] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:127-129. HAN Zi-peng.Rocket exterior ballistic[M].Beijing:Beijing Institute of Technology Press,2008:127-129.(in Chinese)
[14] Murphy C H.Instability of controlled projectiles in ascending or descending flight[J].Journal of Guidance and Control,1981,4(1):66-69.
[15] 程杰,王晓鸣,于纪言,等.次口径非对称鸭舵对修正弹气动特性的影响[J].北京理工大学学报,2015,35(2):133-138. CHENG Jie,WANG Xiao-ming,YU Ji-yan,et al.Study on the effect of sub-caliber asymmetry canards on the aerodynamics of trajectory correction projectiles[J].Transactions of Beijing Institute of Technology,2015,35(2):133-138.(in Chinese)
Analysis on Impact Point Response of a Dual-spin Projectile with Lateral Force Based on Equivalent Force Method
WANG Yu,WANG Xiao-ming,CHENG Jie,YU Ji-yan
(Ministerial Key Laboratory of ZNDY,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)
An equivalent force method is proposed to analyze the impact point response of a dual-spin projectile with lateral control force and calculate the correction of impact point conveniently.The influence of lateral force on the mass-center motion of projectile is separated into two parts:the direct influence arose from the control force and the indirect influence caused by the variation of angular motion related to the control force and moment.Based on the seven-degrees-of-freedom rigid-body flight-dynamicmodel,the change of angle-of-attack caused by the lateral control force can be derived,thus calculating the equivalent force and the variation of impact point.According to the theoretical analysis,the correction distance is almost in proportion to the length between the origin of control force and the mass center under the same condition.Simulations and experiments demonstrate that the errors of correction and phase angle calculated by the proposed method are less than 10%.
ordnance science and technology;dual-spin projectile;lateral force;correction quantity of impact point;lead phase angle
TJ012.3+4
A
1000-1093(2016)08-1379-09
10.3969/j.issn.1000-1093.2016.08.006
2015-12-03
国家自然科学基金项目(11402121)
王钰(1989—),女,博士研究生。E-mail:15250996016@163.com;王晓鸣(1962—),男,教授,博士生导师。E-mail:202xm@163.com

