多级气动液压弹射装置建模及性能研究

任锐，马大为，姚琳，刘峥，何强

（南京理工大学机械工程学院，江苏南京210094）

多级气动液压弹射装置建模及性能研究

任锐，马大为，姚琳，刘峥，何强

（南京理工大学机械工程学院，江苏南京210094）

分析气动液压弹射方式的两种弹射装置类型，研究一种以压缩空气为动力源、油液为传动介质，且具备油液自缓冲结构的多级气动液压弹射装置的弹射性能。针对弹射过程中气腔气体复杂多变过程、封闭油腔油液流动非线性、多级缸运动关系的不确定性及油液缓冲结构，结合真实气体热力学效应，推导封闭油腔油液的压力动态变化模型及多级缸动力学非线性模型，建立描述多级气动液压弹射过程的数学模型；通过数值求解方法，分析该多级气动液压弹射缸的运动规律及弹射性能。研究结果表明：该多级气动液压弹射缸建压过程迅速，并能在0.2s内以2.4m有效弹射行程，将重1.5t负载加速至19m/s，弹射最大过载不超过16g，且相邻两级缸的相对速度不超过15m/s.

兵器科学与技术；压缩空气；多级缸；气动液压弹射

0 引言

气动液压弹射方式，是一种以油液为传动介质，将气体内能转换输出为负载动能的冷弹射技术。该弹射方式具有弹射能源清洁、弹射过程安全、无烟、无光等优点，因此被广泛应用于多种弹射场合，如无人机的发射、机载弹的弹射、靶机的弹射等。

目前，气动液压式弹射装置主要有两种形式:以气囊式蓄能器与液压缸为主的弹射装置［1-4］；以兼具气体腔及油液腔的气体与液体（简称气液）混合缸为弹射机构的弹射装置［5］。一种无人机气液压弹射［6］采用气囊式蓄能器对液压缸充入高压油，并利用活塞杆和滑轮组弹射无人机以达到合适起飞速度。该弹射装置的弹射性能依赖于滑轮组的增速倍率，且需要保证滑轮组缆绳能够在承受动载时不会发生较大的塑性变形。分析及实验结果表明，当仅采用气囊式蓄能器和单级液压缸对小型负载弹射时，弹射速度不超过10m/s，弹射速度较低［7］。

在以气液混合缸为弹射机构的相关研究中，文献［8］设计了一种单级气液混合式弹射系统，通过控制大流量油液迅速充入气液混合缸的油液腔推动单级活塞杆伸出，并排出伸出端气体腔气体，进而弹射负载。但采用单级缸形式，使得最高弹射速度受限于密封构件所能承受的最大相对运动速度。对此，一种多级气液混合缸被提出应用于冷弹射装置中［5］。相较于单级弹射，多级缸形式既可降低相邻构件的相对运动速度而降低密封难度，又可以增大弹射行程而提升最高弹射速度。当采用控制阀对瞬时大流量流体实施控制时，由于一定体积流量气体的质量流量远小于相同体积流量油液的质量流量，而在相同的控制规律和开口截面积下更易于实现对气体流量精确控制；则相较于3级同步液压弹射装置［9］，多级气动液压缸采用气体腔作为动力腔更易于被精确控制，从而更易于实现对弹射性能的控制。但这种以高压气体为压力源、油液为传动介质的多级气动液压弹射装置，弹射性能有待验证。

考虑采用气动液压弹射方式弹射负载的问题，本文提出了一种以压缩空气为动力源、具备油液缓冲结构的多级气动液压弹射装置，并在建模分析过程对已知气动液压弹射的建模方法［10］做出改进，即舍弃对弹射过程中高压气体的理想气体模型假设而考虑其真实热力学特性；并将高压气体复杂热力学特性与多级液压缸动力学模型相结合，提供了一种描述多级气动液压弹射特性的理论模型，通过数值计算得出了所提弹射装置弹射重型负载的弹射性能。该研究提供了一种新的弹射思路，并基于改进的气动液压建模理论给出了描述多级气动液压弹射的理论模型，为今后对多级气动液压弹射装置的优化设计提供参考依据。

1 弹射装置组成及原理分析

一种多级气动液压弹射装置主要由高压气瓶、气动阀、气液混合多级弹射缸及负载组成。高压气瓶储存压缩空气，作为弹射装置动力源。多级气液混合弹射缸作为弹射动力机构，主要由主缸体、充油端盖、进气端盖、多级油缸及密封结构组成。多级弹射缸内部分为气腔及包含多级套筒式油缸的油液腔，其中油液腔可分为多级缸内腔C1、1级有杆腔C2、2级有杆腔C3、3级有杆腔C4、节流缓冲外腔C5、节流缓冲内腔C6.该气液混合多级弹射缸示意结构如图1所示。

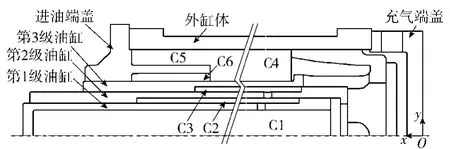
图1　3级气液混合弹射缸结构示意图Fig.1 Schematic diagram of three-stage pneumatic and hydraulic ejection cylinder

弹射时，高压气瓶内压缩空气迅速充入气体容腔，推动第3级油缸，使3级有杆腔油液通过周向通孔流入油腔内部，推动内部各级油缸伸出；内部各级缸的有杆腔油液则通过各级缸的周向通孔流入油腔内部，推动第1级油缸加速伸出，由第1级缸实现对负载的加速弹射。并且，第3级缸的活塞端可与进油端盖形成变截面节流缓冲结构，其余各级缸间主要通过形成油柱与卸荷槽实现油液缓冲。

该弹射装置结合多级缸优势，轴向安装空间小而弹射行程大，且具备弹射能源装置体积小、便携、高效，及油液润滑而摩擦力小的优势。由于弹射装置以油液为传动介质，刚度大、固有频率高，与纯气体或蒸汽弹射相比，更易对弹射过程实施控制。虽然该弹射装置具备上述优点，但弹射动力过程复杂，有必要对其弹射性能进行分析。

2 理论建模及仿真分析

该弹射装置的弹射机理复杂，主要表现为:1）弹射过程中，高压气瓶及气体容腔内压缩空气的热力学效应呈现复杂多变过程；2）油腔内各级活塞缸相对运动关系无法确定，且各级缸动力学特性呈现非线性；3）封闭油腔内，各级缸相对位置变化导致各级缸周向孔口的闭合状态不断变化，引起各子腔室流量的强非线性。由于实际弹射过程中诸多参数是时变的，为便于对弹射机理进行建模，作以下假设:1）弹射过程中油液性质不变，油液特性参数为常量；2）不计油液泄漏，各子油腔内压力视为均匀分布；3）各子油腔的孔口流动视为薄壁孔口流动；4）不计油液在流动过程中所产生的液动力。

引入符号函数sign（x）:x＞0时sign（x）=1；x＜0时sign（x）=-1；x=0时sign（x）=0.

2.1充气过程热力学分析

基于标准干空气模型，对高压气瓶内压缩空气充入气体容腔的热力学过程进行分析。假定充气弹射过程为等熵过程，不计气体泄漏因素，则根据高压气瓶、气体容腔工质的质量连续性方程、能量守恒方程及气体的对应态维里方程，可得压缩空气充气弹射过程的热力学方程为

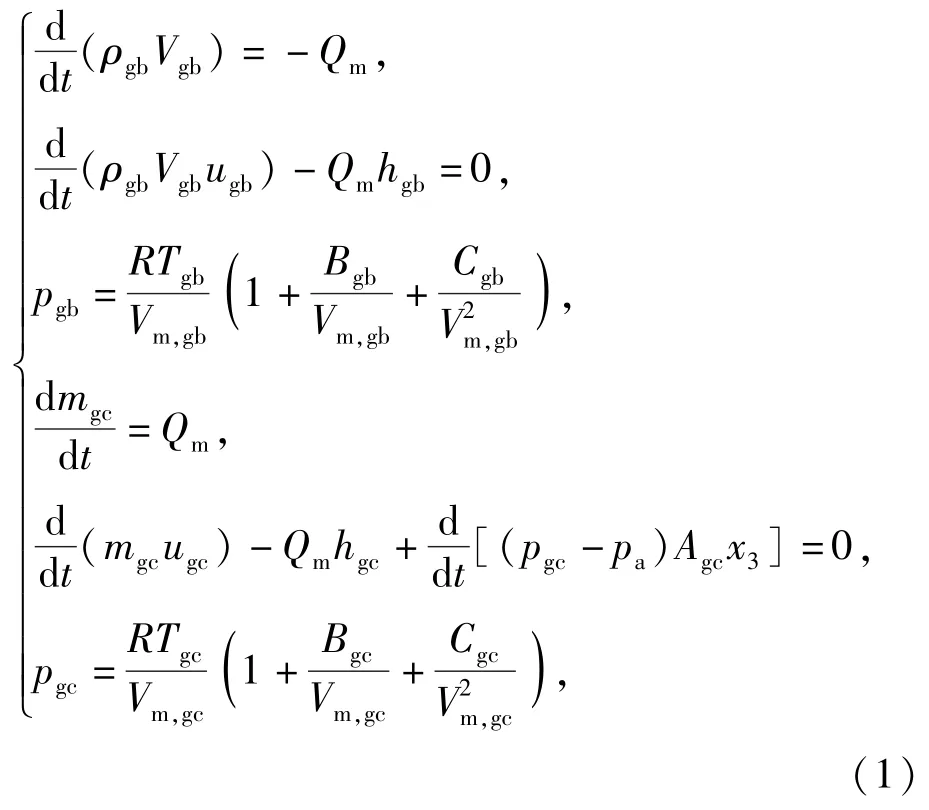
式中:下标“gb”对应高压气瓶工质参数，下标“gc”对应气体容腔内工质参数；ρgb为气瓶中气体密度；Vgb为气瓶容积；R为摩尔气体常数；mgc为多级缸气腔内气体的质量；pgb、pgc分别为气瓶、气腔内气体压力；pa为大气压力；Vm，gb、Vm，gc分别为气瓶、气体容腔内气体摩尔体积；Tgb、Tgc分别是气瓶、气腔内气体温度；uj、hj分别为高压空气的比热力学能和比焓，Bj、Cj分别为对应态第2和第3维里系数，uj、hj、Bj、Cj是关于气体温度Tj的函数［11］，下标j为gb或gc；Agc、x3分别为气腔有效推力面积及第3级油缸的位移；Qm为充气过程中压缩空气的质量流量，结合亚声速及声速两种流动，可得

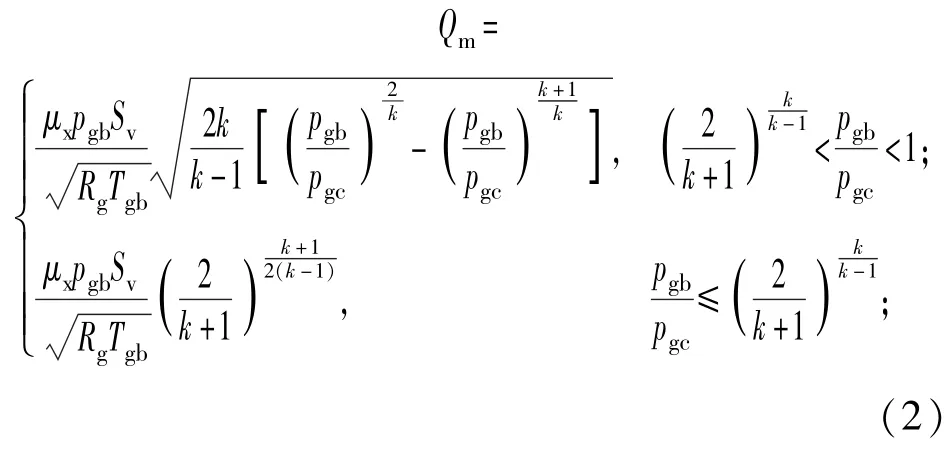
μx是流量修正系数，Sv是气动阀的阀口截面积，k为空气绝热指数，Rg为空气气体常数。

2.2油腔压力动态特性分析

如图1所示，在充气端盖底端处建立固定坐标系，记各级缸位移和速度分别为xi、vi，相邻两级缸相对位移为xir，相对运动速度为vir；第i级缸的通孔个数为ni，孔口截面积为Si，孔口面积梯度为wid.上述参数中i=1，2，3，分别表示第1、第2、第3级油缸。Cj腔油液初始体积为VCj0，瞬时油液容积为VCj，油压为pCj，Cj=C1，C2，C3，C4，C5，C6；油液有效弹性模量为β，油液密度为ρ；孔口流量系数Cd.

记3级缸到达缓冲位置前的运动行程为L3，第1、第2级缸相对运动行程为L12，第2、第3级缸相对运动行程为L23；第2级缸活塞轴肩和活塞尾端与第3级缸通孔端部距离分别为L2zj、L2wd；第1级缸活塞轴肩和活塞尾端与第2级缸通孔距离分别为L1zj、L1wd.

2.2.1腔室C4、C5、C6压力动态特性

1）当x3r≤L3时，C6、C5、C4视为具有相同的压力变化特性:

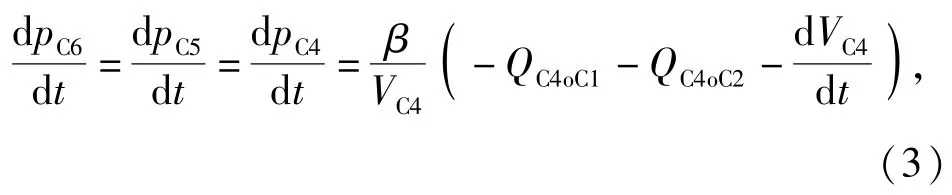
式中:C4腔流出至第2级有杆腔C3流量为

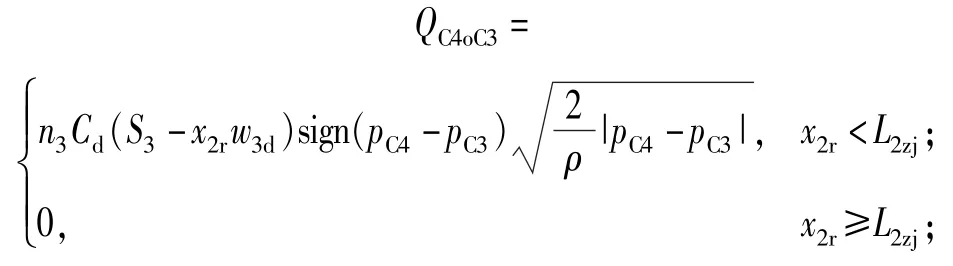
C4腔流出至内腔C1流量为

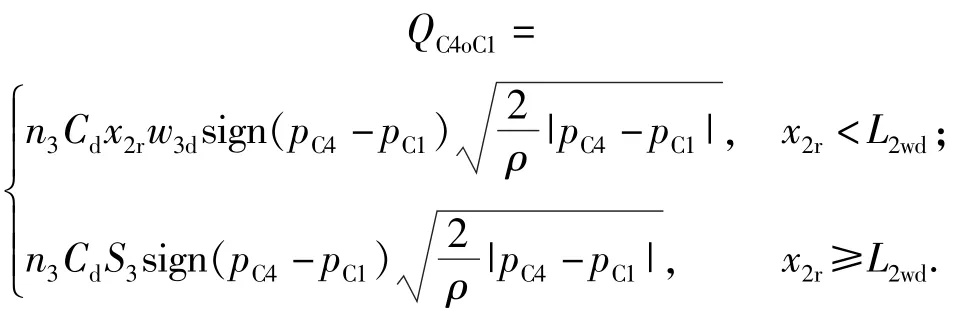
2）当x3r＞L3时，如图2所示，第3级油缸的异型活塞部分与进油端盖的薄壁结构共同起到节流缓冲的作用。假定C4腔压力保持不变:

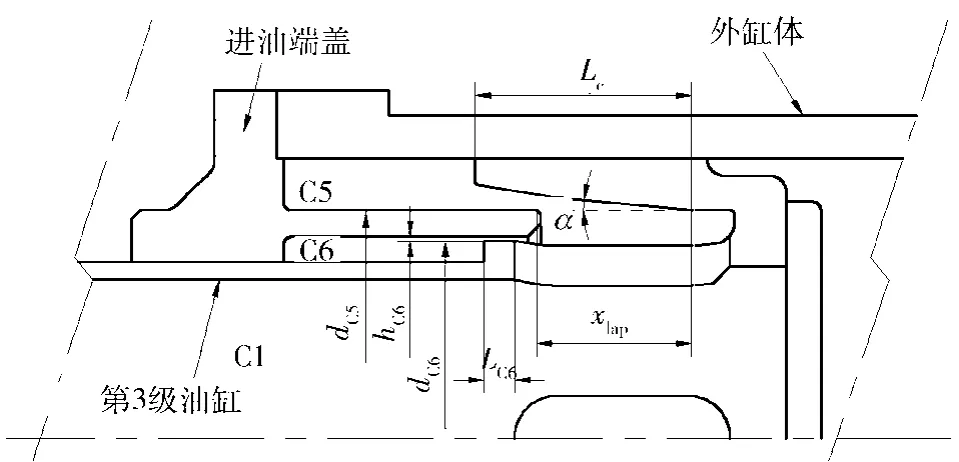
图2　节流缓冲结构示意图Fig.2 Schematic diagram of throttle buffering structure

采用环形缝隙流量公式求C6腔流出流量:

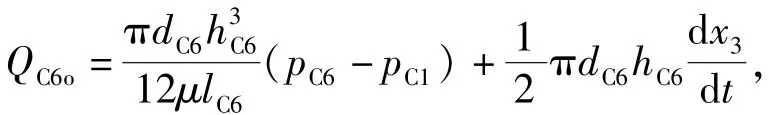
式中:hC6为环形缝隙高度；dC6为内环直径；lC6为间隙长度；μ为油液动力粘度。

采用圆锥阀变截面开口流动的流量公式求得C5腔流出流量:

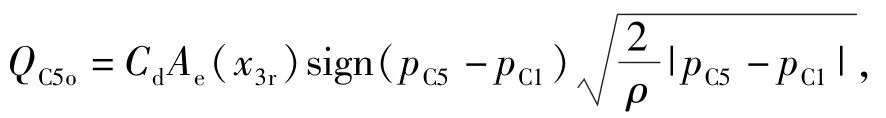
式中:有效通流截面积

Ae（x3r）=πxlap（dC5+xlapsin2δ）sinδ，

xlap=Lc-（x3r-L3），Lc为缓冲行程，δ为锥面倾斜角度。则节流缓冲内腔C6压力特性:

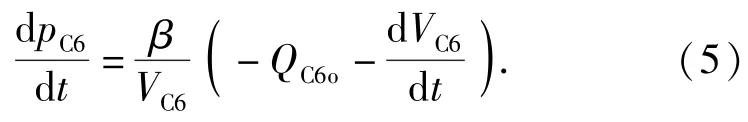
节流缓冲外腔C5的压力特性:

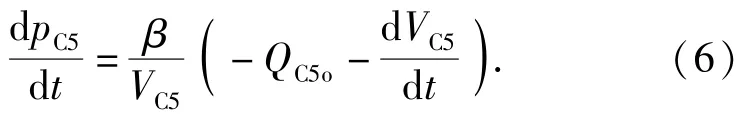
2.2.2容腔C3压力动态变化特性

式中:流入C3腔的流量QC3i=QC4oC3；流出C3腔的流量为QC3o=QC3oC2+QC3oC1，QC3oC2、QC3oC1分别是从C3腔流出至C2腔和C1腔的流量。

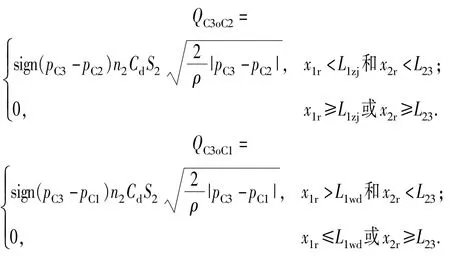
2.2.3容腔C2压力动态特性

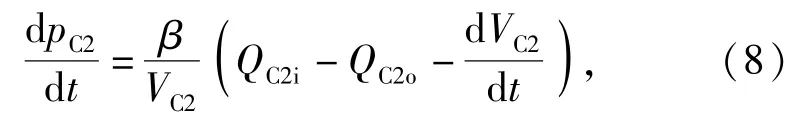
式中:流入C2腔的流量QC2i=QC3oC2；流出C2腔的流量为

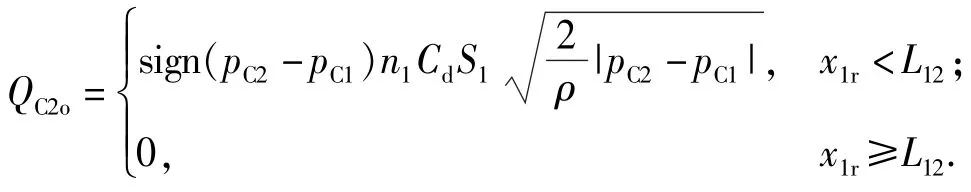
2.2.4容腔C1压力动态特性

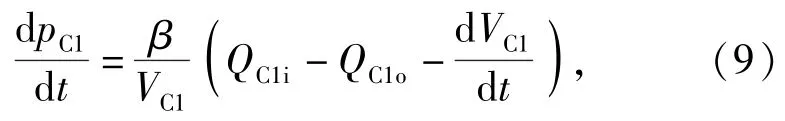
式中:第1级有杆腔油液瞬时体积为VC1=VC10+（x1-x2）A2+（x2-x3）A3，A2、A3分别为第2、第3级缸最大内径所对的截面面积；流入流量QC1i= QC4oC1+QC3oC1+QC2o；流出流量QC1o=0L/min.

2.3多级缸动力学过程

各级缸受力如图3所示，Ffi表示相邻两级缸间摩擦力，Fisc、Fidh、Fizj分别表示第i级缸活塞杆伸出端、活塞端挡环底端及活塞端轴肩处的受力，i=1，2，3；F2dhn表示2级缸活塞挡环内侧受力。

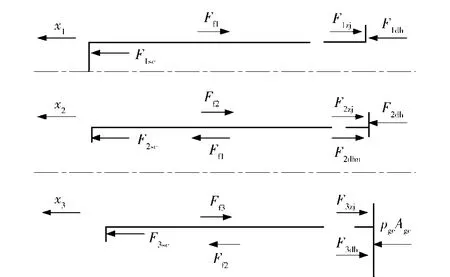
图3　各级油缸1/2简化结构受力示意图Fig.3 Force diagram of half of each cylinder

当相邻两级缸的相对位移近乎为0时，会发生接触；当相邻两级缸发生最大相对位移时，两级缸间形成油柱缓冲，且通过卸荷槽以避免困油。当发生上述两种相互作用时，Fisc、Fidh不再是油压作用力，并由接触碰撞模型［12］计算得出:

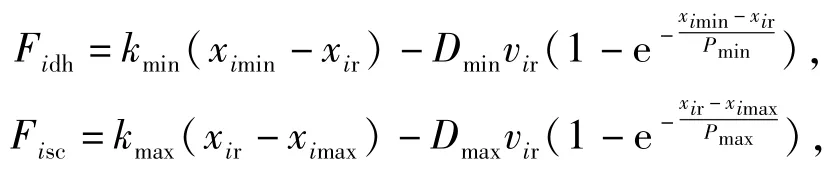
式中:kb、Db、Pb分别为接触碰撞的接触刚度、粘性摩擦系数及最大允许穿透量，b=min，max，分别对应于最小位移处碰撞和最大位移处碰撞的参数；ximin、ximax分别为相邻缸允许的最小相对位移及最大相对位移，i=1，2，3.

则多级缸弹射过程的动力学方程为

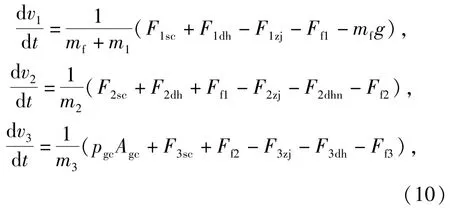
2.4弹射过程非线性数学模型

选取状态变量Y=［y1；y2；y3；y4；y5；y6；y7；y8；y9；y10；y11；y12；y13；y14；y15；y16］，其中y1=ρgb，y2= Tgb，y3=mgc，y4=Tgc，y5=x1，y6=v1，y7=x2，y8=v2，y9=x3，y10=v3，y11=pC1，y12=pC2，y13=pC3，y14=pC4，y15=pC5，y16=pC6.根据（1）式～（10）式，建立多级气动液压弹射装置弹射过程的数学模型:

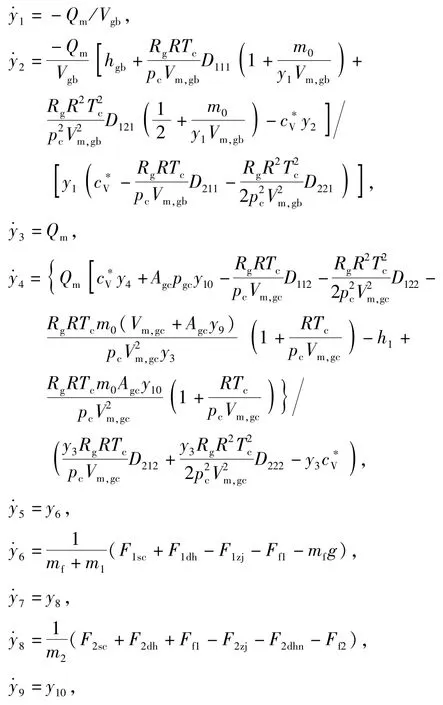
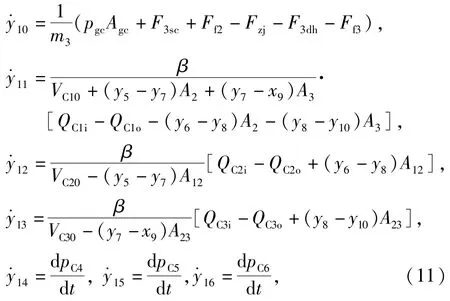
式中:c*V为理想气体的比定容热容；Tc、pc分别为干空气临界温度和临界压力；m0为空气摩尔质量；A12为第1级缸活塞杆外侧与第2级缸内侧所构成的圆环截面积；A23为第2级缸活塞杆外侧与第3级缸内侧所构成的圆环截面积；D211、D221为高压气瓶内气体温度Tgb的函数；D112、D122、D212、D222为气体容腔内气体温度Tgc的函数［13］。

在Matlab中将所得微分方程组编写为M程序，通过4阶龙格-库塔法对该微分方程组进行求解。仿真模型各状态参量的初始值及主要参数设置如下:ρgb=227.3kg/m3；Tgb=Tgc=300K；mgc=1.293× 10-4kg；vi=0m/s，i=1，2，3；pCj=0.3×106Pa，Cj= C1，C2，C3，C4，C5，C6；x1=0.021m；x2=0.011m；x3=0.001m；μx=0.96；Sv=0.0004m2；k=1.4，R= 8.314J/（mol·K-1）；Rg=287.0041J/（mol·K-1）；Vgb=50L；Tc=132.5K；pc=3.77×106Pa；m0= 0.0289586kg/mol；ρ=850kg/m3；β=700MPa；L12=L23=0.81m；L2zj=0.018m；L1zj=0.01m；L4= 0.78m；L3=L1wd=0.026m；L3=0.78m；hC6=0.002m；dC6=0.24m；lC6=0.02m；Lc=0.05m；δ=0.21rad；mf=1500kg.

3 结果分析

3.1充气过程分析

由图4可知，弹射装置所用高压气瓶初始压力为20MPa.弹射初始时，多级缸气腔的初始压力即为大气压力0.1MPa；各级油缸内油腔的初始压力均设定为0.3MPa.在弹射过程中，由于高压气瓶为固定容积，随着压缩空气充入多级弹射装置的气体容腔内的过程，高压气瓶内气体密度减小，质量减小，压力不断下降。

结合图5和图6所示的多级弹射缸位移、速度曲线可知:弹射初始时刻，由于负载重力及弹射缸内油腔油液压力作用，各级缸未发生相对位移，气体容腔体积不变，从而高压气瓶充入多级弹射缸气体容腔内的气体压力迅速增加，作用于第3级缸的推力增大；当推力大于第3级缸的油液阻力时，第3级缸运动，同时油液腔油液流动，第1级缸和第2级缸以相同速度同时伸出。上述从开始充入气体，气体压力增大至推动各级缸发生运动的过程，称为初始建压过程。

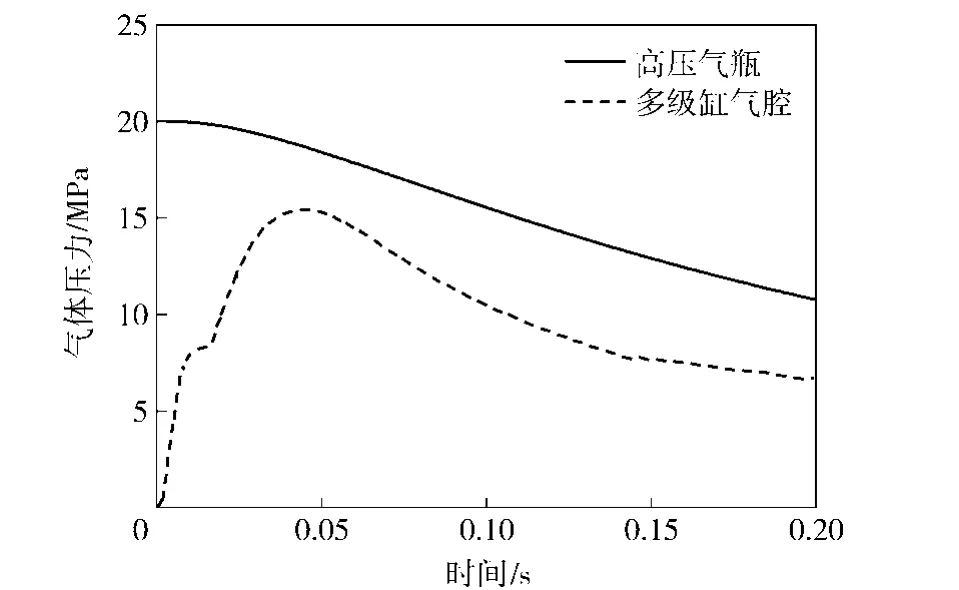
图4　气体压力曲线Fig.4 Gas pressure

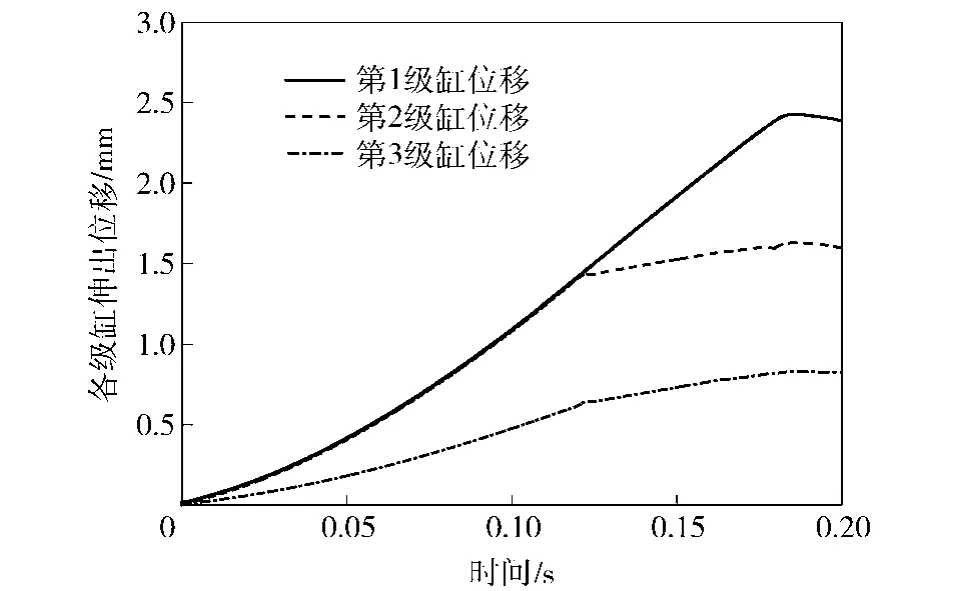
图5　多级弹射缸位移曲线Fig.5 Displacement curves of multi-stage catapult cylinders

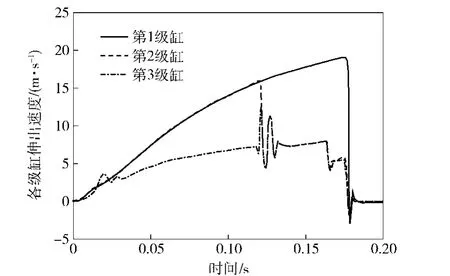
图6　多级弹射缸速度曲线Fig.6 Velocity curves of multi-stage catapult cylinders

完成建压过程后，气体容腔压力增长减缓，随后再迅速达到峰值，而后逐渐减小。主要是因为第3级缸伸出初始速度增大，气体容腔体积增长率大，导致气体容腔压力增长率减小；由于多级缸中各油液腔的油液存在流通关系的非连续性，初始运动时刻，第2级缸和第3级缸的相对移动逐渐使得C4腔油液不再流入C3腔而仅流入C1腔，3级缸油液阻力增加，速度略有下降，则气体容腔体积增长缓慢，从而再次迅速增加，并达到峰值压力15.4MPa；气体容腔压力达到峰值后，流入的气体质量流量不足以弥补因气体容腔体积增大引起的压力降，从而气体容腔压力随着第3级缸的位移增加而逐渐减小。

3.2多级缸运动分析

根据图5和图6可知:多级弹射装置在弹射过程中各级油缸逐级伸出，并且弹射初始阶段，由于第3级缸的油液有效作用面积大于C1腔的油液有效作用面积，在相同流量下，第1级缸和第2级缸的伸出速度大于第3级缸速度；当第2级缸与第3级缸的相对位移达到最大时，第2级缸和第3级缸发生级间油液缓冲，随后以相同速度伸出，第1级缸继续加速伸出，直至第1级缸伸出至最大弹射行程位置处；当第1级缸与第2级缸相对位移达到最大时，第3级缸和第1级缸同时到达截止位置，主要是由于多级弹射缸的内部结构设计，使得3级有杆腔油液全部流出时，各级缸之间的油液恰巧全部流入至内腔C1中，内腔C1中油液体积达到最大。

根据图7和图8可知弹射全过程各子油液腔的压力变化特性。初始时刻各子油液腔压力为0.3MPa；当t＜0.12s时，充入高压气体弹射，由于第2级缸相对第3级缸快速伸出，第3级有杆腔C3的油压较大，而内腔压力最小，且C4、C5、C6腔压力变化规律相同；当0.12s≤t≤0.156s时，第2级缸相对第3级缸达到最大相对位移处，油柱和卸荷槽起缓冲作用，各子油腔压力均出现压力峰值，且pC3达到33MPa；当t=0.156s时，第3级缸运动到缓冲位置处，C4腔压力视为不变，C5和C6腔油压由于节流口作用压力迅速增大，而第1级和第2级有杆腔油压则有所降低，直至各级缸同时达到行程位置处时再次增加。在最大行程位置处，由于负载被弹射出去，各级缸油液腔压力最终均会降低并趋于稳定。

3.3弹射性能分析

根据图5可知，在当前设置的气动阀开口截面积及对所建理论模型的分析前提下，该弹射装置建压过程所需时间约为5ms，建压过程迅速。结合图6，多级弹射缸在弹射过程中，相邻两级缸的相对速度始终不超过15m/s，能在现有密封技术［14］下实现高速弹射。

图9所示的弹射速度曲线比较平稳，并且在多级弹射缸运动到最大行程位置处时达到19m/s的最大弹射速度。根据图10所示的弹射过载曲线，负载在弹射初始阶段达到最大的弹射过载，最大过载约为16g；达到最大过载后，由于气体容腔压力的变化，弹射过载先出现减小，再随着气体容腔压力的增大而增大；在气体容腔压力达到峰值后逐渐减小的过程中，弹射过载也逐渐减小，并在第1级缸相对第2级缸伸出时发生波动。

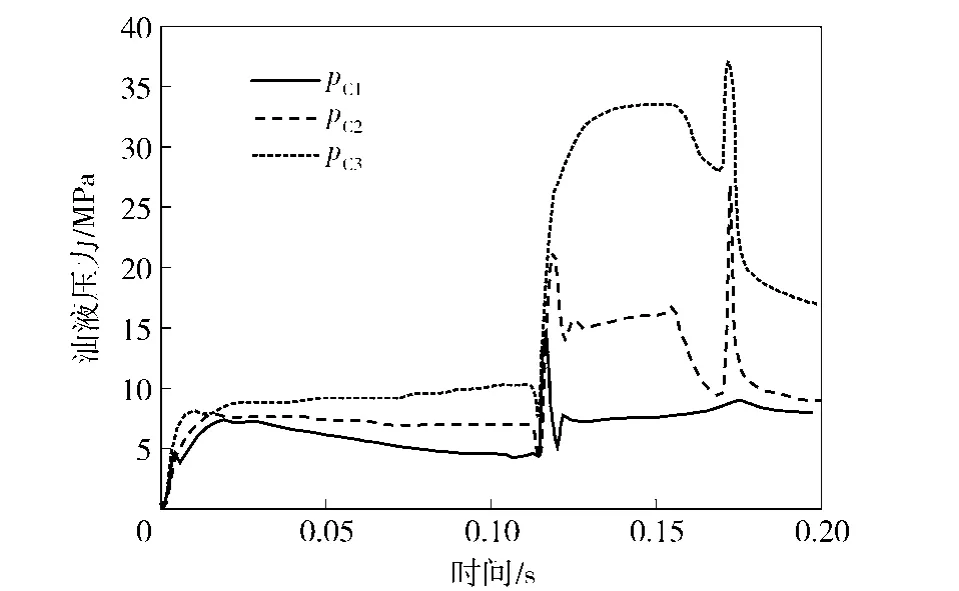
图7　内腔及前两级有杆腔油液压力曲线Fig.7 Changing curves of oil-pressures in inner chamber and the first and second stage rod chambers

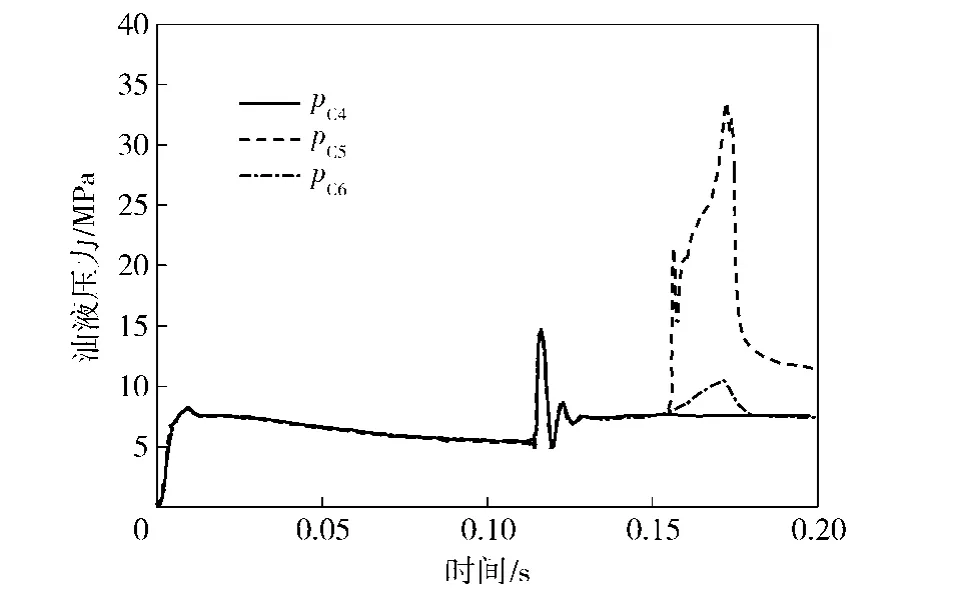
图8　3级有杆腔及缓冲油腔油压曲线Fig.8 Changing curves of oil pressures in the third rod chamber and buffer chambers

图9　弹射速度曲线Fig.9 Ejection velocity curve

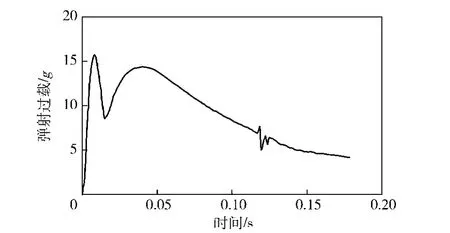
图10　弹射过载曲线Fig.10 Ejection overload curve

4 结论

本文解释了以压缩空气为动力源、多级气液混合缸为弹射机构的多级气动液压弹射装置的弹射原理，提出对该弹射装置弹射性能研究的必要性。通过建立封闭油腔内各子腔室油液压力变化关系，推导各级缸动力学方程，结合基于真实气体效应的压缩空气充气过程的热力学方程，建立了多级气动液压弹射装置的数学模型，并以数值求解得知多级弹射缸为逐级伸出，其弹射性能如下:

以容积50L、初始压力为20MPa的高压气瓶充气弹射时，该多级气动液压弹射装置能在2.4m有效弹射行程内，将重为1.5t的负载弹加速至19m/s，最大弹射过载小于16g；并且弹射过程中，相邻两级缸的相对运动速度不超过15m/s，有效降低了高速弹射时相邻运动构件间的油液密封难度。

（References）

［1］ 赵伟，黄钰曌，俞浙青，等.高速弹射实验装置液压动力系统［J］.浙江大学学报:工学版，2014，48（5）:799-804. ZHAO Wei，HUANG Yu-zhao，YU Zhe-qing，et al.Hydraulic power system of high speed ejection experiment device［J］.Journal of Zhejiang University:Engineering Science，2014，48（5）: 799-804.（in Chinese）

［2］ 马琳.气液弹射机构设计及动态特性研究［D］.杭州:浙江工业大学，2009:12-14. MA Lin.Study on gas-liquid ejection launcher design and dynamic characteristics［D］.Hangzhou:Zhejiang University of Technology，2009:12-14.（in Chinese）

［3］ 张永亮，范文欣，田野.气液压弹射动力学影响参数分析［J］.四川兵工学报，2015，36（1）:56-59. ZHANG Yong-liang，FAN Wen-xin，TIAN Ye.Study on dynamic ejection force of numerical parameters of pneumatic and hydraulic launching［J］.Journal of Sichuan Ordnance，2015，36（1）:56-59.（in Chinese）

［4］ 权凌霄，刘建伟，宋育，等.无人机气液压弹射系统建模与弹射过程仿真分析［J］.液压与气动，2016（1）:71-77. QUAN Ling-xiao，LIU Jian-wei，SONG Yu，et al.Modeling of pneudraulic launching system of UAV and simulation analysis of launching process［J］.Chinese Hydraulics&Pneumatics，2016（1）:71-77.（in Chinese）

［5］ 胡真华，胡爱武，胡宣哲，等.冷弹射方法及装置:中国，20910166299［P］.2010-03-24. HU Zhen-hua，HU Ai-wu，HU Xuan-zhe，et al.Cold ejection method and device:China，20910166299［P］.2010-03-24.（in Chinese）

［6］ 李悦，张海黎.无人机气液压发射原理试验研究［J］.南京航空航天大学学报，2010，42（6）:699-703. LI Yue，ZHANG Hai-li.Principle experiments of hydraulic and pneumatic launching of UAV［J］.Journal of Nanjing University of Aeronautics&Astronautics，2010，42（6）:699-703.（in Chinese）

［7］ 赵伟，阮健，李胜，等.液压弹射机构动力系统研究［J］.兵工学报，2013，34（4）:459-464. ZHAO Wei，RUAN Jian，LI Sheng，et al.Research on power system of hydraulic catapult mechanism［J］.Acta Armamentarii，2013，34（4）:459-464.（in Chinese）

［8］ 阮健，赵伟，李胜.新型气液混合动力弹射装置:中国，201010524849［P］.2011-04-06. RUAN Jian，ZHAO Wei，LI Sheng.Novel hydraulic and pneumatic catapult device:China，201010524849［P］.2011-04-06.（in Chinese）

［9］ 谢英俊.高速液压上抛系统的关键技术研究［D］.杭州:浙江大学，2000. XIE Ying-jun.Researches onfundamental techniques of the hydraulic catapult system［D］.Hangzhou:Zhejiang University，2000.（in Chinese）

［10］ 李悦，裴锦华.无人机气液压发射动力学数值仿真［J］.机械工程学报，2011，47（8）:183-190. LI Yue，PEI Jin-hua.Dynamic numerical simulation of the pneumatic and hydraulic launching of UAV［J］.Journal of Mechanical Engineering，2011，47（8）:183-190.（in Chinese）

［11］ 杨风波，马大为，杨帆，等.高压弹射装置内弹道建模与计算［J］.兵工学报，2013，34（5）:527-534. YANG Feng-bo，MA Da-wei，YANG Fan，et al.Interior ballistics modeling and calculation of high-pressure ejection device［J］.Acta Armamentarii，2013，34（5）:527-534.（in Chinese）

［12］ 董富祥，洪嘉振.多体系统动力学碰撞问题研究综述［J］.力学进展，2009，39（3）:352-359. DONG Fu-xiang，HONG Jia-zhen.Review of impact problem for dynamics of multibody system［J］.Advances in Mechanics，2009，39（3）:352-359.（in Chinese）

［13］ 杨风波，马大为，朱忠领，等.基于真实热力学过程分析的气动弹射性能研究［J］.机械工程学报，2013，49（24）: 167-174. YANG Feng-bo，MA Da-wei，ZHU Zhong-ling，et.al.Pneumatic catapult performance research based on the true thermodynamic process analysis［J］.Journal of Mechanical Engineering，2013，49（24）:167-174.（in Chinese）

［14］ 成大先，王德夫，姜勇，等.机械设计手册［M］.第5版.北京:化学工业出版社，2008:21-299. CHENG Da-xian，WANG De-fu，JIANG Yong，et al.Mechanical design handbook［M］.5th ed.Beijing:Chemical Industry Press，2008:21-299.（in Chinese）

Theoretical Modeling and Performance Research on Multi-stage Pneumatic and Hydraulic Catapult Device

REN Rui，MA Da-wei，YAO Lin，LIU Zheng，HE Qiang
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

A novel multi-stage pneumatic and hydraulic catapult device with oil buffering structure，which utilizes compressed air as impetus and hydraulic fluid as transmission medium，is introduced and its ejection performance is researched by analyzing two typical catapult devices involving pneumatic and hydraulic catapult.According to the complex polytropic process of gas，the flow nonlinearity of hydraulic fluid in enclosed chamber，motion uncertainty of multi-stage cylinders and the self-buffering structure，a mathematical model describing multi-stage pneumatic and hydraulic catapult process is established based on real gas thermodynamic effect.Meanwhile，the dynamic variation model of oil pressure in enclosed chamber and the nonlinear dynamic model of multi-stage cylinders are constructed.The motion laws and working performance of multi-stage pneumatic and hydraulic catapult cylinder are obtained through numerical simulation.The results show that the proposed multi-stage pneumatic and hydraulic catapult device can generate the appropriate pressure quickly and accelerate the load up to 19 m/s within 0.2 s with the speed-up distance of 2.4 m，and thus the overload is less than 16 g and the relative velocity between two adjacent cylinders is less than 15 m/s.

ordnance science and technology；compressed air；multi-stage cylinder；pneumatic and hydraulic catapult

TJ768

A

1000-1093（2016）08-1365-08

10.3969/j.issn.1000-1093.2016.08.004

2015-12-24

武器装备预先研究项目（51328020106）

任锐（1993—），男，博士研究生。E-mail:jasonray_njust@163.com；马大为（1953—），男，教授，博士生导师。E-mail:ma-dawei@mail.njust.edu.cn