基于最大相关最小冗余的多标记特征选择

杨文元



基于最大相关最小冗余的多标记特征选择

杨文元*

(闽南师范大学福建省粒计算重点实验室，福建漳州363000)

针对多标记学习中高维数据运行速度问题，提出一种基于最大相关最小冗余的特征选择算法ML-MRMR。利用数据与标记的互信息，获得了最大相关性最少冗余性特征集合。分析了所选特征百分比与精度关系。实验结果表明，所提出算法在速度和精度上都具有明显的优势。

多标记学习；特征选择；最大相关最小冗余；数据降维

引言

随着计算机网络和信息化的发展，网络数据和资源呈海量特征，数据的标注结构复杂程度也在增加，传统的单标记方法无法满足对复杂数据进行分析处理的需求，以机器学习技术为基础的多标记学习技术现已成为一个研究热点，其研究成果广泛地应用于各种不同的领域，如图像视频的语义标注、功能基因组、音乐情感分类以及营销指导等[1, 2]。多标记学习的主要特点在于它能反映真实世界对象具有的多义性。因此，在最近十年来,多标记学习已逐渐吸引国内外许多一流的学术机构和科学研究者。

多标记问题定义和评价指标是一个研究热点。由于多标记学习输出空间的类别标记集合数随着标记空间的增大而成指数规模增长，当标记空间具有k个类别标记时，则可能的类别标记集合数为2k，为了有效应对标记集合空间过大所造成的学习困难，学习系统需要充分利用标记之间的相关性来辅助学习过程的进行，基于考察标记之间相关性的不同方式，有一阶策略、二阶策略、高阶策略等多标记学习问题求解策略[3]。在多标记学习问题中，由于每个对象可能同时具有多个类别标记，因此传统监督学习中常用的单标记评价指标，如精度（accuracy）、查准率（precision）、查全率（recall）等，无法直接用于多标记学习系统的性能评价。因此，研究者们相继提出了一系列多标记评价指标，总的来看可分为两种类型，即“基于样本”的评价指标[4-6]以及“基于类别”的评价指标[7]。

多标记学习的问题转换和算法适应是另一个研究热点[3, 8]。问题转换方法是将多标记问题转换为其它已知的学习问题进行求解，代表性学习算法有一阶方法Binary Relevance[9]，该方法将多标记学习问题转化为“二类分类”问题求解；二阶方法[10]，该方法将多标记学习问题转化为“标记排序”问题求解；高阶方法[11]，该方法将多标记学习问题转化为”多类分类”问题求解。算法适应直接执行多标记分类方法,是解决问题的完整形式，通过对常用监督学习算法进行改进，将其直接用于多标记数据的学习。代表性学习算法有一阶方法ML-kNN[12]，该方法将k近邻算法进行改造以适应多标记数据；二阶方法Rank-SVM[13]和CML[5]，Rank-SVM将核学习算法SVM进行改造以适应多标记数据。

数据量增大的同时，数据的维度也越来越高，在多标记学习过程中，高维数据训练和测试需要更多的计算时间和空间。因此，降低高维数据的维度是多标记学习中一个重要的研究课题。

特征提取和特征选择是两种主要的降维方法：特征提取通过某些原始特征映射到低维空间变换[14]，然后生成一些新的特性；特征选择目的是找到一个给出一定的预先确定的标准的最优特征子集[15,16]。特征选择不仅减少了许多特征个数，使得学习算法效率更高，而且可以提高多标记学习的性能，因为它可以避免过拟合现象。

在高维数据中，特征数量往往较多，但其中存在大量冗余或不相关的特征，特征选择是从原始特征集中，按照某一评价准则选择出一组具有良好区分特性的特征子集。特征选择能剔除冗余或不相关的特征，从而达到减少特征个数、提高模型精确度、减少运行时间等目的，同时，选取出的特征更有利于理解模型与分析数据[17]。

针对对多标记学习中高维数据问题，本文基于FisherScore提出多Multi-label FisherScore (MLFS)算法，首先，对高维数据进行特征选择，其次，分析精度与特征选择率关系，最后，所提出的方法与现有的特征选择算法相比，实验结果表明，该算法具有明显优势。

1 特征选择相关工作

按照特征选择是否独立学习算法，特征选择技术可以分为封装方法和过滤方法。封装方法用学习算法评价特征的重要性[18]，即围绕挖掘算法“封装”特征选择过程，如贝叶斯分类器、支持向量机和聚类[19, 20]。封装方法的计算代价通常较高[21]，因为需要反复训练学习算法，因而对多标记学习中的高维数据算处理可能不是有效的。过滤方法分析数据的内在特征，并在学习任务前根据某些准则选择一定数据排名最高的特征[22]。是一个纯粹的预处理工具，与学习算法无关，因此过滤方法比封装方法更有效。

许多特征选择方法使用两个特征之间的依赖度来评价特征，而不是使用独立特征和特征子集之间的特性。利用相似性矩阵并引入矩阵分解技术进行特征选择，它提供了一个整批处理模式搜索特征。例如，Nie等人提出了一个健壮的特征选择标准，使用结合L2,1范数最小化损失函数和正则化[23]。Farahat等人提出了一种矩阵分解标准特征选择，提供了一个高效的贪婪算法[24]。杨等人提出了一个有效的多任务特征选择的在线学习算法，在节约时间复杂性和内存花费上显示其巨大的优势[25]。Song等人构建一个用于特征选择使用Hilbert-Schmidt独立性标准的框架，是基于好特性应该是与标记高度相关的假设。赵等人介绍了相似性特征选择标准，包含许多广泛使用的标准[26]。

本文提出基于最大相关最小冗余的特征选择算法，作对比的典型特征算法主要是：Relieff特征选择的策略是随机选择实例,并根据最近邻的特征相关性设置权重，Relieff是特征选择中是最成功的策略之一[27]；Kruskal-Wallis则使用样本间总体方差方差进行测试[28]，已成为MATLAB函数kruskalwallis。

2 评价指标

根据多标记学习的两个任务，即多标记分类和标记排名，评价指标也分为两类：基于分类方法和基于排名方法[2,3]。

2.1 基于分类的评价指标

基于分类的评价指标有Average precision和Hamming loss，Average precision是一种最直观的评价方式，评价样本的预测标记排名中排在相关标记前面的也是相关标记的概率平均，计算公式如下所示[3]

Hamming loss通过计算多标记分类器预测出的标记结果与实际标记的差距来度量多标记分类器的性能，计算公式如下所示[3]

2.2 基于排名的评价指标

One-error，该方法评价每个样本的预测标记排名中，排在第一位的标记不在该样本的相关标记集中的概率评价，计算公式如下所示[3]

Coverage，该方法评价每个样本的预测标记排名中需要在标记序列表中最少查找到第几位才可以找出所有与该样本相关的标记，计算公式如下所示[3]

Ranking loss，该方法评价所有样本的预测标记排名中，不相关标记在相关标记前面的概率的平均，计算公式如下所示[3]。

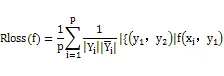
3 最大相关最小冗余特征选择

3.1 最大相关最小冗余

最大相关最小冗余是基于互信息的特征选择方法，它根据最大统计依赖性准则来选择特征[30]。从特征空间中寻找与目标类别有最大相关性且相互之间具有最少冗余性的m个特征，最大相关和最小冗余的定义为[30,31]：

(2)

其中: S表示特征集合; c表示目标类别; I( xi; c)表示特征i 和目标类别 c之间的互信息； I( xi，xj) 是特征i与特征 j 之间的互信息．给定两个随机变量x和y，它们之间的互信息根据其概率密度函数 p( x) 、p( y) 和 p( x，y) 分别定义为

对于多元变量Sm和目标类别c，互信息定义为

(4)

综合公式（3）和（4），MRMR的特征选择标准为

公式（5）表示应该选择与类别最大相关而与候选特征最小冗余的特征．假定已确定一个有 m个特征的数据集 Sm，下一步需要从数据集{S－Sm}中选择使得式( 4) 最大化的第 m + 1个特征为

(6)

3.2 基于MRMR多标记特征选择算法

依据上述公式可以实现单标记特征选择算法MRMR[30]，没有考虑多个类别同时存在的情况，不适于多标记数据的特征选择。为克服这一缺陷，本文将MRMR算法扩展到多标记问题中，提出一种多标记数据特征选择算法：ML-MRMR算法。算法如下：

算法：ML-MRMR

输入：数据矩阵，标记矩阵，特征选择百分比k 输出：特征选择集 1: 初始化矩阵Matrix_rank2: for i =1 to multi-label 3: rank= MRMR(train_data, train_target(i)) //由公式（1）到（6）计算4: Matrix_rank=Matrix_rank+ rank 5: end for 6: ，从而选择得到特征向量I

4 实验及分析

实验中，多标记学习的四个数据集来源于公开数据集，特征选择运行速度明显提高，同时精度等评价指标也提高。数据集的具体情况见表1所示。

表1 数据集基本描述

4.1 评价指标结果

对比的四个算法分别是不进行特征选择NSF、Relieff、KruskalWallis、MRMR[27-29]，所有算法及评价基于ML-KNN[32]，采用十折交叉验证，实验结果见表2所示。

平均精度（Ave. Prec.）越大表明算法越好，其他四个指标Coverage、Hamming loss、One-error、Ranking Loss是越小表明算法越好，从表中可以看出，ML-MRMR特征选择算法明显好于其他算法。特别值得提到的是ML-MRMR的算法的所有指标都好于NSF，其原因是通过最大相关最小冗余的选择，过滤掉了冗余特征而保留优化的特征子集，有效提高精度和降低误差，并提升了高维数据的多标记学习速度，整体提高学习模型的性能。

4.2 特征选择百分比分析

所选特征百分比与学习精度关系，图1-4显示基于相似矩阵的ML-MRMR特征选择算法的学习精度大于未作特征选择的学习精度，当全部选择时则两者精度一样。ML-MRMR特征选择算法在选择20-60%特征达到最高精度，增加特征后精度反而有所下降，这是表明全部特征中存在一定的冗余特征，反而影响精度。

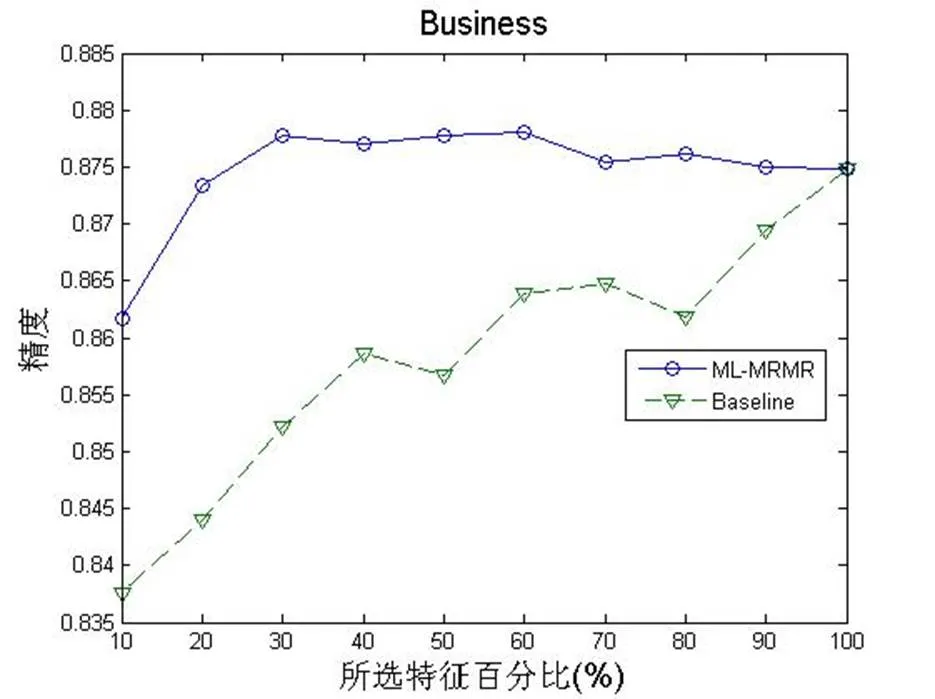
图1 Business精度与所选特征百分比关系

图2 Computers精度与所选特征百分比关系

图3 Reference精度与所选特征百分比关系

图4 Science精度与所选特征百分比关系

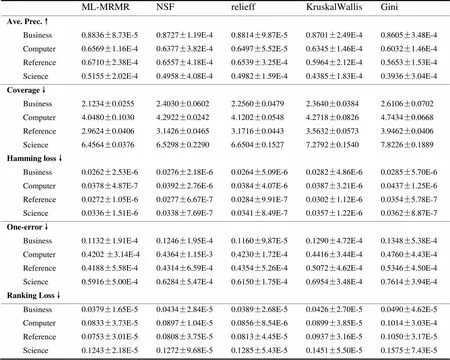
表2 实验结果

5 结语

本文针对多标记学习中高维数据的降维问题提出一种有效的降维技术，通过最大相关最小冗余找到一个最相关信息的特征子集，利用ML-MRMR去除冗余特征而选择有效特征的新方法。对四个公开数据集，该方法与现有算法相比，实结果表明，该算法具有快速和精度高等明显优势。

[1] G. Tsoumakas and I. Katakis, Multi-Label Classification: An Overview. 2007.

[2] 李思男, 李宁, and 李战怀, 多标记数据挖掘技术:研究综述. 计算机科学, 2013(04): p. 14-21.

[3] M. L. Zhang and Z. H. Zhou, A Review on Multi-Label Learning Algorithms. Ieee Transactions on Knowledge and Data Engineering, 2014. 26(8): p. 1819-1837.

[4] R. E. Schapire and Y. Singer, BoosTexter: A boosting-based system for text categorization. Machine Learning, 2000. 39(2-3): p. 135-168.

[5] N. Ghamrawi and A. McCallum, Collective multi-label classification, in Proceedings of the 14th ACM international conference on Information and knowledge management. 2005, ACM: Bremen, Germany. p. 195-200.

[6] S. Godbole and S. Sarawagi, Discriminative Methods for Multi-labeled Classification, in Advances in Knowledge Discovery and Data Mining, H. Dai, R. Srikant, and C. Zhang, Editors. 2004, Springer Berlin Heidelberg. p. 22-30.

[7] G. Tsoumakas and I. Vlahavas, Random k-Labelsets: An Ensemble Method for Multilabel Classification, in Machine Learning: ECML 2007, J. Kok, et al., Editors. 2007, Springer Berlin Heidelberg. p. 406-417.

[8] T. Grigorios and K. Ioannis, Multi-Label Classification: An Overview. International Journal of Data Warehousing and Mining (IJDWM), 2007. 3(3): p. 1-13.

[9] M. R. Boutell, J. B. Luo, X. P. Shen, and C. M. Brown, Learning multi-label scene classification. Pattern Recognition, 2004. 37(9): p. 1757-1771.

[10] J. Furnkranz, E. Hullermeier, E. L. Mencia, and K. Brinker, Multilabel classification via calibrated label ranking. Machine Learning, 2008. 73(2): p. 133-153.

[11] G. Tsoumakas and I. Vlahavas, Random k-labelsets: An ensemble method for multilabel classification, in Machine Learning: ECML 2007, Proceedings, J.N. Kok, et al., Editors. 2007, Springer-Verlag Berlin: Berlin. p. 406-417.

[12] M. L. Zhang and Z. H. Zhou, ML-KNN: A lazy learning approach to multi-label leaming. Pattern Recognition, 2007. 40(7): p. 2038-2048.

[13] A. Elisseeff and J. Weston, A kernel method for multi-labelled classification, in Advances in Neural Information Processing Systems 14, Vols 1 and 2, T.G. Dietterich, S. Becker, and Z. Ghahramani, Editors. 2002, M I T Press: Cambridge. p. 681-687.

[14] I. Guyon and A. Elisseeff, Feature extraction: foundations and applications, Vol. 207. 2006: Springer.

[15] I. Guyon and A. Elisseeff, An introduction to variable and feature selection. Journal of Machine Learning Research, 2003. 3: p. 1157-1182.

[16] Y.M. Yang and J.O. Pedersen. A comparative study on feature selection in text categorization. in International Conference on Machine Learning. 1997.

[17] 黄莉莉, 汤进, 孙登第, and 罗斌, 基于多标记ReliefF的特征选择算法. 计算机应用, 2012(10): p. 2888-2890+2898.

[18] H. Liu and L. Yu, Toward integrating feature selection algorithms for classification and clustering. IEEE Transactions on Knowledge and Data Engineering, 2005. 17(4): p. 491-502.

[19] J. Weston, S. Mukherjee, O. Chapelle, M. Pontil, T. Poggio, and V. Vapnik. Feature selection for SVMs. in Advances in Neural Information Processing Systems. 2000.

[20] M. Dash, K. Choi, Peter Scheuermann, and Huan Liu. Feature selection for clustering - a filter solution. in IEEE International Conference on Data Mining. 2002.

[21] R. Kohavi and G.H. John, Wrappers for feature subset selection. Artificial Intelligence, 1997. 97(1-2): p. 273-324.

[22] L. Yu and H. Liu. Feature selection for high-dimensional data: a fast correlation-based filter solution. in Proceedings of the Twentieth International Conference on Machine Learning. 2003.

[23] F.P. Nie, H. Huang, X. Cai, and C. Ding. Efficient and robust feature selection via joint $_2,1$-norms minimization. in Advances in Neural Information Processing Systems. 2010.

[24] A.K. Farahat, A. Ghodsi, and M.S. Kamel, Efficient greedy feature selection for unsupervised learning. Knowledge and information systems, 2013. 35: p. 285-310.

[25] H.Q. Yang, M.R. Lyu, and I.King, Efficient online learning for multitask feature selection. ACM Transactions on Knowledge Discovery from Data, 2013. 7(2): p. 1-27.

[26] Z. Zhao, L. Wang, H. Liu, and J.P. Ye, On similarity preserving feature selection. Knowledge and Data Engineering, IEEE Transactions on, 2013. 25(3): p. 619-632.

[27] H. Liu and H. Motoda, Computational Methods of Feature Selection, 2008: Chapman & Hall.

[28] L. J. Wei, Asymptotic Conservativeness and Efficiency of Kruskal-Wallis Test for K Dependent Samples. Journal of the American Statistical Association, 1981. 76(376): p. 1006-1009.

[29] H. Long Peng, F. Ding C., Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005. 27(8): p. 1226-1238.

[30] H.C Peng, F.H Long, and C. Ding, Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005. Vol. 27(No. 8): p. pp.1226-1238.

[31] 丁建睿, 黄剑华, 刘家锋, and 张英涛, 基于mRMR和SVM的弹性图像特征选择与分类. 哈尔滨工业大学学报, 2012(05): p. 81-85.

[32] ZHANG ML, ZHOU ZH.ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognition, 2007. 40: p. 2038-2048.

Feature Selection via Max-Relevanceand Min-Redundancy in Multi-label Learning

YANG Wenyuan*

(Lab of Granular Computing, Minnan Normal University, Zhangzhou, Fujian 363000, China)

High dimensional data affects the speed of multi-label learning. This paper proposes the ML-MRMR algorithm for multi-label feature selection. By using the mutual information of data and labels, the features of maximum correlation and minimum redundancy obtained. The relationship between precision and selected percent of features is also analyzed. Experimental results show that the ML-MRMR algorithm is better than existing ones in terms of speed and precision.

multi-label learning; feature selection; max-relevance and min-redundancy; dimensionality reduction

1672-9129(2016)02-0021-05

TP181

A

2016-09-13；

2016-09-24。

国家自然科学基金61379049。

杨文元（1967－)，男，博士，副教授，主要研究方向：机器学习、粒计算。

(*通信作者电子邮箱yangwy@mnnu.edu.cn)