基于变分模型的块压缩感知重构算法

陈建，苏凯雄，杨秀芝，郑明魁，林丽群



基于变分模型的块压缩感知重构算法

陈建，苏凯雄，杨秀芝，郑明魁，林丽群

（福州大学物理与信息工程学院，福建福州350116）

为了提高现有块压缩感知重构算法的性能，提出了基于全变分和混合变分模型的块压缩感知（简称BCS-TV和BCS-MV）算法。该方法以块为单位进行图像采样，以自然图像正则项的稀疏性为先验条件，通过变型的增广拉格朗日交替方向乘子法(ALM-ADMM)，在整幅图像范围内逼近目标函数来重构原始图像。与以前基于一致性块采样的压缩感知工作对比，该算法的PSNR约提高1.5 dB，SSIM约提高0.05，运行速度较稳定，特别适合具有固定传输时延的多媒体数据处理场合。

全变分；图像重构；块压缩感知；交替方向乘子法

1 引言

压缩感知（CS）理论[1~3]表明，只要信号在某个变换域具有稀疏性，就能利用一个与变换基不相干的观测矩阵，将原始高维信号投影到一个低维空间上。利用这些少量的观测值，即可实现信号的精确重构。但对于大尺寸的数据（如图像、视频），直接的压缩采样所需的存储空间巨大，且复杂度很高。

为了降低图像的采样代价，文献[4~10]研究了自然图像的块压缩感知（BCS）。在测量方法上， Lu和Thong等[4,5]提出了基于块对角结构的随机矩阵和结构化随机矩阵（SRM），但理论依据欠缺，且重构质量有待于提高。此后，Thong和Armin等[8,9]分别探讨了这2类矩阵的受限等距性质(RIP)，为BCS测量方法提供了理论依据。另一方面，为了提高该测量方案的重构效率，Fowler等[6,7]结合平滑投影算法和方向性小波变换，提出了基于块压缩感知的平滑投影兰德韦伯重构（BCS-SPL, block compressed sensing and smoothed projected landweber reconstruction）算法，并将其应用到视频压缩和多视点编码中。为了降低块效应，BCS-SPL在每次迭代时都使用维纳滤波器进行图像平滑，但该步骤会模糊图像的边缘。为了保持图像的边缘像素，文献[10]将图像分解为高低频2个分量分别处理，并添加了锐化空域滤波器和高斯平滑滤波器，虽然有效提高了重构质量，但也增加了重构复杂度。

针对现有块压缩感知重构算法（BCS-SPL）的滤波步骤未考虑图像自身特点，以及重构复杂度较高的问题，本文将具有良好边缘特性和去噪性能的高效全变分模型引入到块压缩感知重构中，以求能够在较低复杂度的条件下，高保真地重建自然图像。为了提高该重构算法的通用性，进而将该模型推广到可容纳多种稀疏正则项的混合变分模型，以适用于更多类型的图像。

2 相关理论

2.1 压缩感知

根据CS理论[1~3]，在变换域具有稀疏性的信号（），可通过一组与变换基（）不相干的测量向量，投影得到测量值，即

其中，原始信号的尺寸为×1，为域的稀疏系数，是×l的测量值，是×的测量矩阵（<<）。常用的测量矩阵有高斯矩阵、贝努利矩阵等。

信号重构问题即求解式（1）中的。由于远小于，故是一个病态方程求解问题。可以通过式（2）先求出稀疏系数，即求解l最小范数下带约束的优化问题

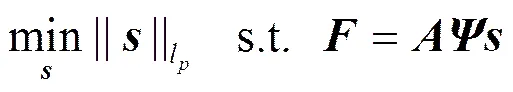
最后由式（1）的约束条件=恢复出原始信号。目前主流的压缩感知重构算法主要有凸优化、迭代阈值以及贪婪法算法[11]。其中，凸优化算法中的TV（全变分）[12,13]不仅能够保持良好的边缘特性，而且具有较好的去噪性能，因此备受关注。

2.2 块压缩感知

为了减轻计算量和存储器负担，一些学者将基于块的测量方案[4]引入压缩感知中。块压缩感知将每幅图像分为N个非重叠的块（尺寸为×，为块序号），并通过合适的矩阵（尺寸为M×2）进行测量，得到

将式（3）的块压缩感知应用于整帧图像等效于按照式（1）进行压缩感知，仅需满足为块对角矩阵，即

(4)

当稀疏基也具有类似的块结构时，解码端可以按块重构，如BCS-SPL-DCT。由于基于块的重构存在块效应现象，基于式（2）的帧重构方法优于块重构，如基于DWT（离散小波变换），DDWT（离散双树小波变换）和CT（轮廓波变换）的BCS-SPL算法[6,7]。

2.3 高效全变分重构算法

TVAL3[12,13]是一种基于增广拉格朗日交替方向乘子法（ALM-ADMM）的TV改进算法，不仅重构质量好，而且收敛速度很快。TVAL3在TV模型基础上引入变量，并增加一个约束项，表示图像的离散梯度，其正则化模型可表示为

相应的增广拉格朗日问题为

(6)

其中，λ和λ是拉格朗日乘子的2个分量，β和β是惩罚参数。重构过程采用交替方向算法分别求解和子问题，以及更新拉格朗日乘子，第+1次迭代为

(8)

(9)

此外，为了保证重构精度，由小到大更新惩罚参数，其中为比例系数。

(11)

2.4 混合变分不等式框架

TV模型实际上是受线性约束的可分离的凸优化问题式（13）[14]的一个特例

He等[14~16]提出了针对该问题的混合变分不等式（MVI）统一框架，其标准形式为

求解式（14）的分裂算法详见文献[14~17]，而ALM-ADMM则是该算法在=2时的一个特例。文献[14,17]证明了基于MVI统一框架的重构算法的最差收敛速率为。这为全变分模型能够进一步推广为混合变分模型，以及具有稳定的重构速率提供了理论依据。

3 块压缩感知变分重构算法

为了在低复杂度和稳定速率条件下高效地重构图像，本文在块压缩感知的重构中引入全变分（TV）及混合变分（MV）模型，利用整幅图像正则项的稀疏先验知识，提出BCS-TV和BCS-MV的测量及重构方法。下面分别阐述其基本流程、重构模型、算法及性能分析。

3.1 基本流程

1) 分块排列

先将图像分为N个非重叠的块（每块尺寸为×），然后采用一个合适的扫描方式将每个图像块转化为维的列矢量（=1,2,…,N）

= P

其中，= [1,…,]，P代表分块排列操作符。

2) 按块测量

通过测量矩阵（尺寸为M×）分别对每个图像块列矢量进行测量, 得到N列观测值（=1,2,…,N）

=

N列组合成观测值矩阵=[1,…,]，等效于对进行测量，即

=

3) 按帧重构

以整幅图像梯度模的稀疏性为先验知识，由和重构出图像块列矢量空间

= convex_rec (,)

4) 反扫描和整合

对恢复的每个图像块列矢量进行反扫描，并整合成完整的重构图像

=−1

其中，−1代表分块排列逆过程。

3.2 重构模型

当图像相邻点像素值差异较大时会产生较大的梯度值，由于大多数自然图像具有分段光滑[2,7]的特性，因此其梯度模具有良好的稀疏性，结合测量操作和分块排列的约束条件，可构造块压缩感知重构的正则化模型

其中，参数定义同前文所述，对应的增广拉格朗日函数为

(16)

最小化L(，，，)问题可以分解为如下4个子问题。

1)子问题

2)子问题

(18)

3)子问题

4)子问题

(20)

需要说明的是，式（16）和式（17）中的−为重构误差，表示整幅图像的离散梯度，根据自然图像的梯度稀疏特性，的非零值个数很少。寻求同时满足重构误差最小和全局离散梯度最小的解，即是所求重构图像。

3.3 重构算法

BCS-TV沿用TVAL3中分别采用一步最速下降法和类收缩法求解和子问题，仅增加计算量很小的和的转换操作。

具体的重构算法如下。

算法1 Function BCS-TV

输入值：,

输出值：

迭代过程：

while（不满足外循环截止条件）

while（不满足内循环截止条件）

第+1次迭代：

1)子问题

①计算L关于的次梯度g

②计算BB步长α

2)子问题：式（18）

3)子问题：

4)子问题：式（20）、式（21）

内循环结束

更新惩罚参数：式（11）、式（12）

外循环结束

当然，这种BCS-TV算法很容易推广到含多个正则目标的混合变分模型，只需将式（15）中的和扩展为多个分量。

比如增加一个表示小波域稀疏性的正则项，则式（15）扩展为

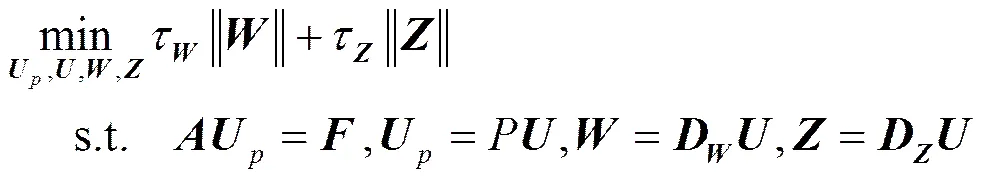
其中，D和D分别表示求梯度和小波变换，τ和τ分别表示这2个正则项的权重系数，对应的重构算法扩展为算法2。

算法2 Function BCS-MV

输入值：,

输出值：

迭代过程：

while（不满足外循环截止条件）

while（不满足内循环截止条件）

第+1次迭代：

1)子问题

类似算法1的第①到④步

2)子问题：式（18）

3)子问题

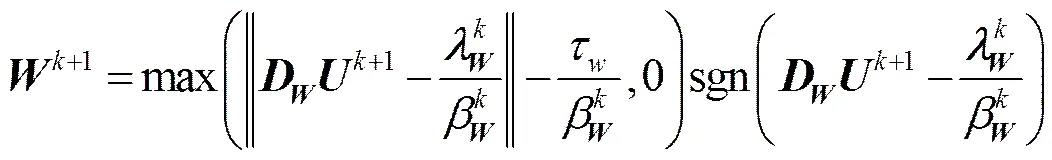
4)子问题

5)子问题：式(20)、式(21)

内循环结束

更新惩罚参数：式(11)、式（12）

外循环结束

实际上，BCS-MV是BCS-TV的分量扩展，BCS-TV则是BCS-MV的一个特例。

3.4 性能分析

本节以BCS-SPL-DCT、BCS-SPL-DWT、BCS- SPL-DDWT和BCS-SPL-CT[6,7]为参照，分析BCS-TV和BCS-MV的性能。由于上述算法均是采用一致性的分块采样，故采样复杂度相同，均为，大大低于不分块直接采样方式的()。

6种算法的主要区别在于重构。在测量方式相同的情况下，图像的变换系数越稀疏，重构质量就越高。BCS-SPL每轮迭代过程都要进行一次像素域的维纳滤波和变换域的阈值收缩，兼顾了图像的分段平滑特征和变换域稀疏性。其中，BCS-SPL-DCT重构过程中针对图像块进行稀疏变换，因而重构图像存在块效应，需要滤波消除。而其他3种BCS-SPL重构过程中都是针对整幅图像做稀疏变换，重构质量优于BCS-SPL-DCT，又由于图像在DDWT和CT域的能量比DWT域更集中，即更稀疏，因而BCS-SPL-DDWT和BCS-SPL-CT的重构质量更好。但是前4种算法的维纳滤波环节没有考虑图像自身信息，统一采用一个3×3的滤波模板，可能会造成图像的过渡平滑，从而影响图像恢复质量。BCS-TV每次迭代都交替地逼近关于误差和梯度的增广拉格朗日函数的最小值，而梯度最小化反映在重构图像上自然就会具有分段平滑特征。此外，梯度变换系数近似图像边界，TV域的稀疏性与CT域相当，因而在梯度域具有良好的稀疏性。然而对于纹理图像，TV域的稀疏性欠佳，DWT、CT和DDWT域稍好。BCS-MV则在BCS-TV基础上添加了诸如小波约束的正则项，适用于具有光滑和纹理特征的图像。

在重构复杂度上，BCS-SPL每轮迭代需要进行一次维纳滤波（fil），2次递归投影（pro)、2次变换（dct、dwt、ddwt和ct分别运行一次正变换和一次反变换，计算量相当）、若干次图像分块重排和逆过程（rank，正反排列重组计算量相当），以及针对不同变换系数的阈值收缩（shr)。前4种算法的主要计算量在于变换和阈值收缩部分，ddwt最复杂，dct最简单，dwt和ct居中。而BCS-TV和BCS-MV则包含子问题的一步最速下降（osd)，子问题的块排序变换（rank)，和子问题的类收缩（shr_like_w和shr_like_z），以及若干(lam)和(beta)分量的更新等步骤。上述步骤都有显式求解，可以折合成有限个标量或矢量的乘法和加法。其主要运算量在p、及子问题，BCS-TV在这2步中包含多次采用矢量减法的梯度变换和反变换，计算复杂度比需采用矢量乘法的dct更低，BCS-MV由于需要多计算dwt的正反变换，故计算复杂度居中。

根据上述分析，表1和表2归纳了影响参考算法和本文算法的重构质量和复杂度的要素。

表1 重构质量要素对比

表2 重构复杂度对比

综上所述，可知BCS-SPL-DCT、DWT、DDWT、CT的重构质量级别分别是最差、中等、良好、良好，复杂度级别为较低、中等、高、中等。BCS-TV重构性能良好，复杂度最低；BCS-MV重构质量最好，复杂度居中，合理分配BCS-MV各正则项的权值可以在重构质量和速度间取得较好的平衡。此外，由于本文算法具有可计算的收敛性保证[14,17]，重构速度随测量率变化波动不大。

4 实验测试

为验证本文算法的性能，采用Matlab软件对4种BCS-SPL（-DCT、-DWT、-DDWT、-CT）和本文算法（BCS-TV、BCS-MV）进行仿真测试，以重构前后图像的峰值信噪比（PSNR）和结构相似度(SSIM）反映重构质量，以重构时间反映计算复杂度。测试素材取自6幅尺寸为256×256的经典灰度图像lenna、goldhill、barbara、mandrill、peppers和bridge，图像块的尺寸设为32×32（即==32），按列扫描。已知高斯矩阵与任意稀疏基线性无关[3,11]，故以之为测量算子。为了公平起见，小波和双树小波变换均采用4层，轮廓波按参考程序默认配置。实验平台是配置为Intel(R) Core i5-2520M CPU, 主频2.50 GHz，内存3.05 GB的联想笔记本。

6种块压缩感知重构算法的、和重构时间曲线如图1~图3所示。

上述各图展示了几种块压缩感知重构算法在不同采样率下重构质量和时间代价的对比情况。可以看出，BCS-SPL-DCT的重构性能最差，BCS-SPL-DWT优于-DCT，但仅对barbara做很高采样时才能取得最好的。当测量率较小时，BCS-SPL-DDWT重构获得的占一定优势，但是重构时间偏长。随着采样率的增大，BCS-SPL-CT的重构速度优势进一步体现，当仅有bridge获得高于-DDWT的。而BCS-TV重构算法总能取得较好的性能，随着采样率升高，增长最快。尤其对于分段平滑的lenna、goldhill、peppers和bridge，BCS-TV在各种采样率情况下都能取得很高的和。BCS-MV重构的和最高，即使对于纹理丰富的barbara和mandrill也能优于其他算法。本文算法与上述BCS-SPL相比，约提高1.5 dB，约提高0.05 dB。此外，前4种BCS-SPL算法的重构时间都随着采样率的变化产生较大的波动，而BCS-TV和BC-MV的重构时间相对稳定，BCS-TV的运行速度最快，这对于实时处理和重构时间预计具有一定优势。

图4至图9展示了当测量率为50%时，不同测试图像采用BCS-SPL-DDWT、BCS-SPL-CT、BCS-TV、BCS-MV 4种算法重构图像的主观质量对比。

从6组重构效果对比图可以看出，BCS-SPL-DDWT和BCS-SPL-CT算法重构的层次感和对比度较好，但噪声颗粒稍大，舒适度不及本文算法。BCS-TV算法重构的图像比较柔和，噪声小，主观上感觉清晰度和舒适度稍好。BCS-MV重构的清晰度、层次感和舒适度均是最佳。

(a)原始图像256×256 mandrill，采样率50% (b)BCS-SPL-DDWT PSNR:21.9 dB, SSIM:0.70 (c)BCS-SPL-CT PSNR:21.9 dB, SSIM:0.71 (d)BCS-TV PSNR:21.9 dB, SSIM:0.75 (e)BCS-MV PSNR:22.2 dB, SSIM:0.76

(a)原始图像256×256 bridge，采样率50% (b)BCS-SPL-DDWT PSNR:27.1 dB, SSIM:0.81 (c)BCS-SPL-CT PSNR:27.5 dB, SSIM:0.83 (d)BCS-TV PSNR:28.7 dB, SSIM:0.87 (e)BCS-MV PSNR:28.7 dB, SSIM:0.87

5 结束语

为了在低复杂度条件下提高现有块压缩感知重构算法的性能，本文提出了基于变分模型的块压缩感知算法BCS-TV和BCS-MV。编码端首先将图像分解成若干不重叠块，接着按列扫描，然后分块测量得到若干测量值列矢量。解码端首先将接收到的测量值列矢量整合成矩阵，以图像正则项的稀疏性为先验知识，以最小化增广拉格朗日函数为目标，采用变型的交替方向乘子法依次求解子问题，重构出图像块的列矢量空间，最后经过反扫描并组合成图像。其创新点在于：以少量的运算代价将全变分模型应用到块压缩感知重构框架中，并将其扩展为可容纳多个正则项的具有通用性的混合变分模型。对照现有块压缩感知重构算法，仿真结果表明，BCS-TV能取得较好的SSIM和最快的重构速度，BCS-MV的SSIM和PSNR均达最佳，而且它们还具有重构时间随测量率变化波动不大的优点，特别适合具有稳定传输时延的图像和视频等多媒体数据的处理场合。鉴于BCS-MV算法具有灵活的可扩展性，下一步计划将其用于视频压缩感知中，有望提高现有基于块的视频压缩感知的总体性能。

[1] CANDES E, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[2] DONOHO D. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[3] ELDAR Y C, KUTYNIOK G. Compressed Sensing: Theory and Applications[M]. USA:Cambridge University Press, 2012.

[4] LU G. Block compressed sensing of natural images[C]//The 15th International Conference on Digital Signal Processing. Cardiff, c2007: 403-406.

[5] THONG T D, TRAC D T, LU G. Fast compressive sampling with structurally random matrices[C]//The 2008 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP). Las Vegas, USA, c2008: 3369-3372.

[6] MUN S, FOWLER J. E. Block compressed sensing of images using directional transforms[C]//Data Compression Conference(DCC). Snowbird, Utah, c2010: 547.

[7] FOWLER J E, MUN S, TRAMEL E W. Block-based compressed sensing of images and video[J]. Foundations and Trends in Signal Processing, 2012(4): 297-416 .

[8] THONG T D, LU G, NAM H N, et al. Fast and efficient compressive sensing using structurally random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(1): 139-154.

[9] ARMIN E, HAN L Y, CHRISTOPHER J R, et al. The restricted isometry property for random block diagonal matrices[J]. Applied and Computational Harmonic Analysis, 2015, 38(1): 1-31.

[10] VAN T C, DINH K Q, JEON B. Edge-preserving block compressive sensing with projected landweber[C]//The 20th International Conference on Systems, Signals and Image Processing (IWSSIP). Bucharest, Romania, c2013: 71-74.

[11] FOUCART S, RAUHUT H. A Mathematical Introduction To Compressive Sensing[M]. Springer New York Press, USA.2013.

[12] LI C B. An Effcient Algorithm For Total Variation Regularization With Applications To The Single Pixel Camera And Compressive Sensing[D].Rice University, 2009.

[13] LI C B. Compressive Sensing For 3d Data Processing Tasks: Applications, Models And Algorithms[D]. Rice University, 2011.

[14] HE B S, TAO M, YUAN X M. A splitting method for separable convex programming[J]. IMA Journal of Numerical Analysis, 2014, (1): 1-33.

[15] HE B S, LIAO L Z, WANG X. Proximal-like contraction methods for monotone variational inequalities in a unified framework I: Effective quadruplet and primary methods[J]. Computation Optimization Application, 2012, (51): 649- 679.

[16] HE B S, LIAO L Z, WANG X. Proximal-like contraction methods for monotone variational inequalities in a unified framework II: General methods and numerical experiments[J]. Computation Optimization Application, 2012, (51): 681-708.

[17] GU G Y, HE B S, YUAN X M. Customized proximal point algorithms for linearly constrained convex minimization and saddle-point problems: a unified approach[J]. Computation Optimization Application, 2014, (59): 135- 161.

Reconstruction algorithm for block compressed sensing based on variation model

CHEN Jian, SU Kai-xiong, YANG Xiu-zhi, ZHENG Ming-kui, LIN Li-qun

(College of Physics and Information Engineering, Fuzhou University, Fuzhou 350116, China)

The algorithms for block compressed sensing based on total variation and mixed variation (abbreviated as BCS-TV and BCS-MV) models were proposed to improve the performance of current reconstruction algorithms for the block-based compressed sensing. In the measuring phase, an image was sampled block-by-block. In the recovering period, it took the sparse regularization of the natural image as a priori knowledge, and approached the target function within the whole image through the modified augmented Lagrange method and alternating direction method of multipliers (ALM-ADMM). The method proposed achieves average PSNR gain of 1.5 dB and SSIM gain of 0.05 at a more stable running speed, over the previous uniformly block-based compressed sensing. It is particularly suitable for the applications of the multimedia data processing with fixed transmission delay.

total variation, image reconstruction, block compressed sensing, alternating direction method of multipliers

TN911.73

A

10.11959/j.issn.1000-436x.2016011

2014-12-23；

2015-05-11

苏凯雄，skx@fzu.edu.cn

国家自然科学基金资助项目(No.61471124，No.61571129)；福建省自然科学基金资助项目(No.2013J01234，No.2014J01234，No.2015J01251)；福建省科技重大专项基金资助项目(No.2014HZ0003-3)；福建省教育厅基金资助项目(No.JA14065)

The National Natural Science Foundation of China(No.61471124, No.61571129), The Natural Science Foundation of Fujian Province(No.2013J01234, No.2014J01234, No.2015J01251), The Major Technology Project of Fujian Province(No.2014HZ0003-3), The Education Department Project of Fujian Province(No.JA14065)

陈建（1981-），女，福建福州人，福州大学讲师，主要研究方向为视频编解码、压缩感知。

苏凯雄（1959-），男，福建罗源人，福州大学教授、博士生导师，主要研究方向为多媒体通信、数字电视广播。

杨秀芝（1963-），女，山西灵石人，福州大学教授、硕士生导师，主要研究方向为图像处理、数字电视技术。

郑明魁（1976-），男，福建闽侯人，福州大学副教授，主要研究方向为多媒体视频编码。

林丽群（1980-），女，福建莆田人，福州大学讲师、博士生，主要研究方向为图像处理。