基于变点发掘的城市轨道交通客流预测模型
朱广宇,王雨晨,张彭,艾渤,边历嵚
基于变点发掘的城市轨道交通客流预测模型
朱广宇1,王雨晨1,张彭2,艾渤3,边历嵚4
(1. 北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京,100044;2. 北京市交通发展研究中心城市交通运行仿真与决策支持北京市重点实验室,北京,100073;3. 轨道交通控制与国家重点实验室,北京,100044;4. 济南瑞通铁路电务有限责任公司,山东济南,250013)
通过城市轨道交通发展过程阶段变化对其相应的客流变化特点进行分析;基于变点发掘的方法划分出轨道交通客流的不同变化模式,并分析导致客流模式变化的影响因素;通过权重变化有效地结合不同交通状态模式下的变参数自回归求和滑动平均(ARIMA)模型和全局BP神经网络模型,构建城市轨道交通客流组合预测模型;结合某大城市轨道交通线路的实际客流数据,对本文模型的适用性和准确性进行验证。研究结果表明:同一模式区间预测比全局搜索预测更容易获得较高精度预测值,组合模型预测结果相对优于单一模型预测结果。
城市轨道交通;客流预测;变点发掘;组合预测;自回归求和滑动平均模型
城市轨道交通客流预测是借助各种定性、定量预测模型对城市轨道交通客流量进行分析与预测的技术总称。准确的客流预测可以为城市轨道交通的规划、建设及运营管理提供重要的基础信息[1−3],因此,一直受到轨道交通规划设计、运营管理等部门的高度重视。早期的客流预测主要以经典的四阶段法为主[4−5],随着社会经济的发展和人员的流动,客流的交通起止点(OD)调查遇到了很多困难,学者们转而通过发掘轨道交通客流的历史变化规律并分析其变化趋势,由此提出了历史平均模型、时间序列模型、非参数回归模型等客流预测方法[6−8],同时,通过对不同的模型进行组合如定性与定量模型的组合、简单方法与复杂方法的组合等[9−11],构建出组合预测模型[12−13],对历史客流数据的不同变化模式进行分析。目前,随着大城市中轨道交通的线路规模不断扩大,其运营呈现出网络化的特点,客流也随之表现出新的特征[14−16],针对这种新特征,四兵锋等[16]构造了一种并行加权神经网络模型;董升伟[17]给出了针对短时客流的改进的BP神经网络模型;常刚等[18]根据区域路网的时空依赖性,引入了空间模型并提出了改进的STARIMA模型。另外,学者们也研究了多种组合模型,如王建等[19]通过组合基于小波分析的BP神经网络、基于小波分析的ARIMA模型以及BP神经网络预测短时交通流,研究表明组合模型的预测结果要优于单一模型的预测结果。由此可见,随着城市轨道的网络化进程,会有一些新的特征对客流预测的精度产生影响。一方面,客流预测模型的构建借助模式识别的基本思想,以“黑箱”方式构造预测模型;另一方面,可以将城市轨道运营网络化的不同阶段特性变化融合到建模过程中。不同的特征变点会对客流变化产生一定的影响,激发特定的变化状态。由此可以通过组合预测的方式甄别变化状态,也可以借助模式划分的方式,在同状态区间中,提高预测的准确性。基于上述分析,本文作者首先对城轨客流变化模式进行模式划分,然后选取适用于非平稳时间序列预测的ARIMA模型和适用于非线性预测的BP神经网络模型,结合城市轨道交通每日客运量数据构建组合预测模型。
1 城市轨道交通运营变化影响因素分析
随着时间的推移,城市轨道客流受到天气、降水、中小学生寒暑假及法定假日等季节性因素的影响,在不同的影响因素作用下产生不同的季节性客流波动变化,如恶劣天气会使城市轨道客流激增,而春节假期则会让客流骤减。在通勤客流的影响下,城轨客流产生工作日和非工作日的周期性客流变化,周一至周五客流量大幅升高,呈现驼峰型或轮槽型变化,而周末客流量则相对大幅度降低。
从大城市轨道交通新线开通到网络成熟会经历单线运营、线网骨架形成、初步网络化及线网成熟4个阶段[20],在不同的阶段中,由于新线分流、培育吸引客流的作用,城市轨道网络化效应日益明显。随着线路的增多,影响客流变化的因素增多,因素之间的相关性增加,独立性减弱,居民出行选择路径的随机性增强,同一线路上进出客流的对应关系也随之减弱。客流逐渐呈现多种特点:1) 单条线路客流呈凸型或单向增减分布;2) 全网中心区域客流量激增,出现断面客流骤变的闭合环形或大弧度曲线;3) 线网中局部某点客流突变等。因此,在城市轨道交通线路发展的进程中,客流分别具有时间客流波动特性和空间客流不均衡特性。
2 城市轨道交通客流的预测模型
根据所得城市轨道交通客流特征,识别划分不同状态区间采用组合的方式构建预测模型,并在不同的阶段对组合模型采用不同的权重,减少均值阶跃、方差漂移的影响。
2.1 基于变点发掘的状态区间划分
由于交通数据在不同的时间段存在不同数值特征,往往预测精度并不高,但是通过状态变点搜索可以将整体数据分成状态类似的小段,可以有效提高模型的拟合程度。城市轨道日客运量时间序列可以看作由一系列的峰谷形状构成的序列波,其序列上存在着状态相似的时间段,不同时间段代表不同的流量状态,通过对不同状态的客流进行分段拟合回归并将各段序列进行汇总,就可以大大降低预测误差。算法主要是将存在变化的序列分为峰曲线(第1个右斜率不为0的点为正)和谷曲线(第1个右斜率不为0的点为负),峰点和谷点则是求得的右斜率序列中发生正负号改变的点。在峰曲线上,任意2个谷点及之间的峰点构成1个凸波,若序列中除峰点和谷点外再没有其他点,则为简单凸波。同理在谷曲线上也存在凹波和简单凹波。算法实际是对数据曲线抽象成的变化的波通过计算波均值和波离差及其观察函数,在序列中的点间进行变点搜索。
对整体序列或者其中1段,均值和离差可以用统计学公式表示。
整体为:
凸(凹)波为:
其中:{l}为峰曲线上的谷点(或谷曲线的峰点)。
对可能的变点是否保留由观察函数决定,在判定前需要确定最小的状态变点的观察函数值,即控制参数。若观察函数大于先前确定的序列变点控制参数时,当前搜索点予以保留,则认为该点并非真实变点转向下一个搜索点。
观察函数为:
(6)
{(w)}为曲线上的个变点的下标集,且。
具体算法如下:
1) 将城市轨道日客流量时间序列绘制成曲线,为循环次数,为变点个数,为辅助变量。置=1,=1,=0,β=l(=1,…,)。
2) 在曲线上从起,沿着时间轴选取2个凸波,记作(−+1−+2),在2个凸波长度内,求出需求序列的波离差和2个波内的每个点作为中间点的值,并求出最大和最小的*:


3) 变点估计,令:
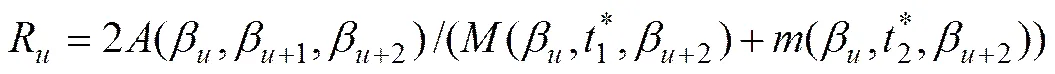
2.2 ARIMA−BP组合模型
ARIMA−BP组合模型对ARIMA模型和BP神经网络模型预测结果进行平均处理,通过赋权后进行加权平均并优化,得到完整的组合模型。其中对具有较高预测精度的预测方法在赋予初值的时候,适当赋予较大权重,对预测精度较低的预测方法所得预测结果赋予较小权重,进而得到优化组合预测模型预测结果。
其中:Z为组合模型预测值;φ为单一预测模型在组合模型中所对应的权重(=1,2,…,);M为单一预测模型预测值(=1,2,…,)。
ARIMA−BP组合模型实施的具体步骤如下:
1) 运用变点识别方法对适当的城市轨道客流数据进行交通状态划分。
2) 根据已有数据,分别运用ARIMA模型以及BP神经网络模型对已存在样本值进行预测。
3) 设置权重,根据ARIMA模型和BP神经网络模型预测结果进行组合预测,输出结果。
4) 根据公式对预测结果和真实值计算方差,方差最小所对应的组合输出权重值,若方差不是最小,则返回步骤3)。
5) 根据已经设定权重,预测未来时刻全线日客运量。
3 实例应用
本文选取某大城市轨道交通某线路2008−01−01—2008−07−31全线日客运量部分数据,对2008−08−01—2008−08−07客流量进行预测。
3.1 城市轨道客流时序特征分析及区间划分
将2008−01−01—2008−07−31全线日客运量数据作为统计对象,绘制全线客运量时间序列图,并通过变点识别方法对其进行分区,如图1所示。

图1 全线日客运量客流变点分区时间序列图
1) 根据变点发掘的方法,时间序列根据状态不同分为8个具有实际意义的模式区间,分别为2008−01−01—2008−02−05;2008−02−06—2008−02− 13;2008−02−14—2008−04−04;2008−04−05—2008−04−09;2008−04−09—2008−04−30;2008−05−01—2008−05−07;2008−05−08—2008−07−19以及2008−07−19—2008−08−07。从图1可见:根据变点发掘方法划分的状态分区基本符合数据的变化趋势,在数据变化较小位置并没有出现变点的记录,而在数据变化剧烈的阶段状态变点较为密集。
通过查阅线路开通时间以及对照节假日等季节性因素,分析可知,2008−02−06—2008−02−13;2008−04−05—2008−04−09以及2008−05−01—2008−05−07这3个区间受到节假日影响,导致日客运量出现大幅度的波动,而2008−07−19—2008−08−07区间则是由于与该线路相连的新线开通,从而导致的客流形态变化,剩余4个分区则均属于无特殊影响因素客流区间。
2) 由图1可知:春节假期客流和其他节假日客流趋势变化相反,呈先降低后升高的趋势,整体客流呈“V”形,而其他假日则均出现不同程度的客流小高峰,工作日客流量基本以周为周期发生波动性变化。
对时间序列进行自相关、偏自相关检验和单位根检验,结果如图2所示。从图2可见:自相关函数值大部分没有出现在置信区间之内,说明数据具有随机性。由于自相关函数和偏自相关函数不随滞后迅速下降到0,单位根(ADF)检验得到的值(−2.531 119)大于显著性水平为1%情况下的值(−4.011 663),则证明时间序列为非平稳序列。所以该序列为一列具有非平稳性、随机性、周期性强的时间序列。
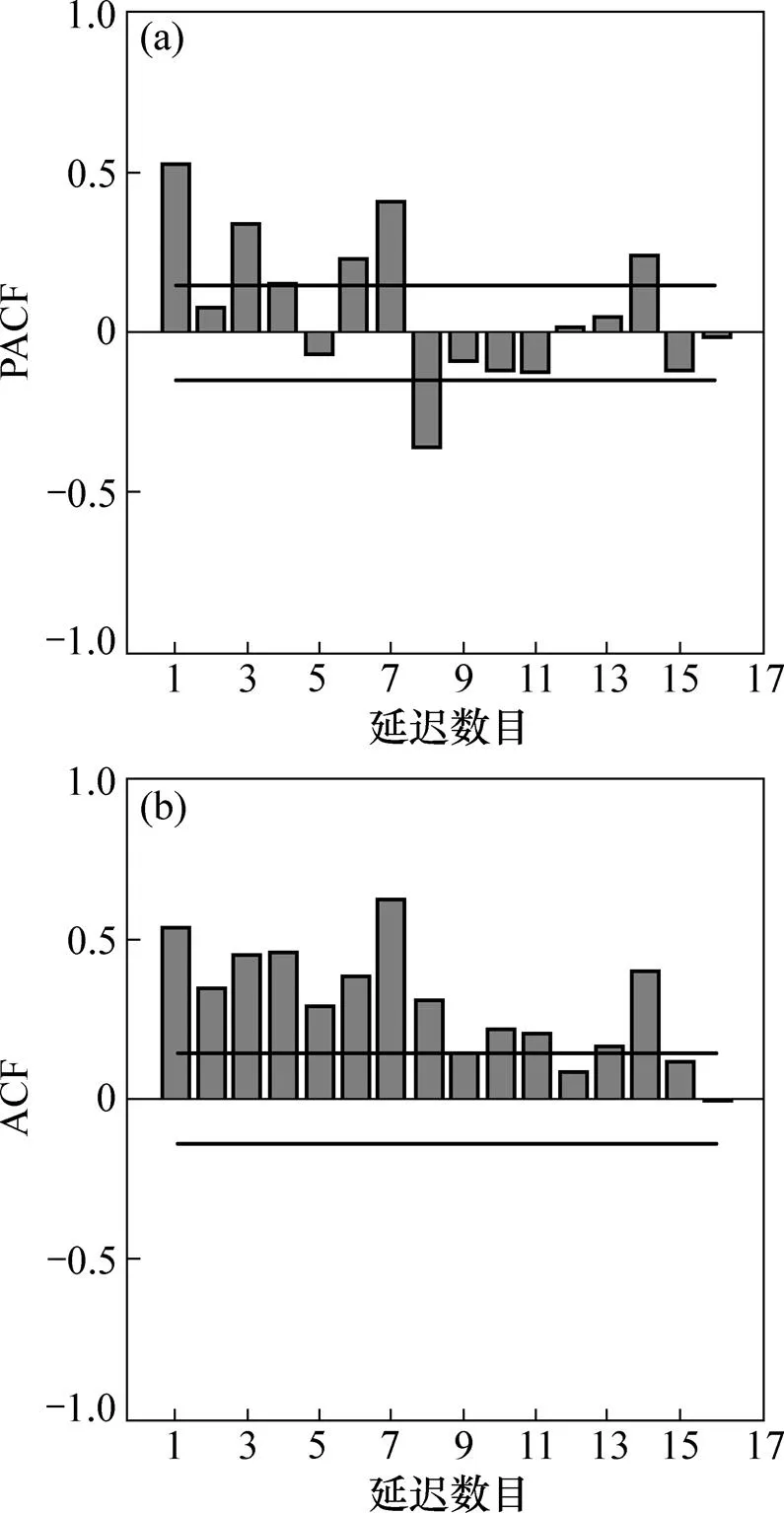
(a) 偏自相关函数;(b) 自相关函数
3.2 面向非平稳客流数据的组合模型预测
3.2.1 基于变点分组区段的ARIMA模型的客流预测
由于考虑到城市轨道客流的随机性,通过变点分组可知,由于2008−08−01—2008−08−07不存在节假日,所以不考虑时间序列的季节性因素,又因为在2008−07−19恰有1条新线与本线相接,连入线网,所以判断8月首周客流属于2008−07−19—2008−08−07 (第8个区段)。因此,本文通过ARIMA模型对第8阶段客流状态进行预测。经过去趋势化得到时间序列恰为平稳性序列,则差分次数=0,通过自相关函数和偏自相关函数以及最小信息准则(AIC)得到=2和=6为最好的模型参数。最后使用ARIMA模型对于2008−08−01—2008−08−07客运量进行预测,得到预测值对比如图3所示。
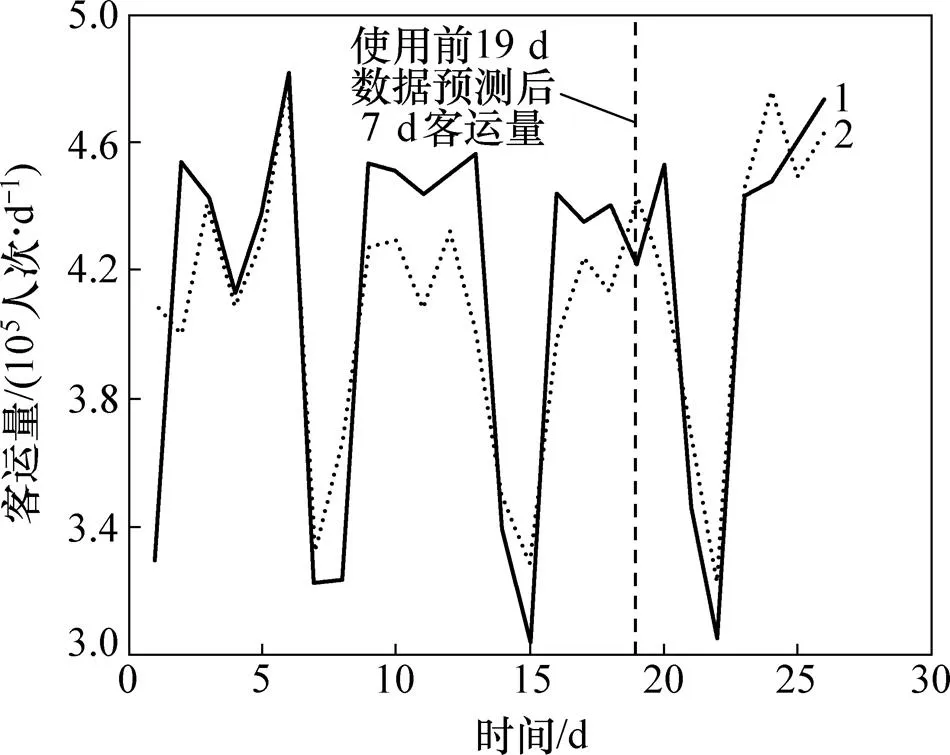
1—真实值;2—预测值。
得到数据并按照公式计算相对误差为:
其中:y为已知数据样本值;z为ARIMA模型预测值。
表1所示为ARIMA模型预测结果相对误差。从表1可以发现:相对误差均在10%之内,预测精度有效。
表1 ARIMA模型预测结果相对误差
Table 1 Prediction relative error of ARIMA model

3.2.2 基于全局数据的BP神经网络模型的客流预测
由于考虑到城轨客流的周期性特征以及预测日期的非节假日属性,通过剔除部分客流量波动剧烈数据,选取25周作为训练数据,通过BP神经网络对第26周进行预测(即2008−08−01—2008−08−07)。前1~25周作为输入数据,第26周作为输出数据。采用3层BP神经网络,中间隐含层节点数选为5个,学习次数为10 000次,误差目标值为0.001。
表2所示为BP神经网络模型预测结果相对误差。从表2可知:相对误差几乎均处于10%,一半以上相对误差在5%以下,预测结果具有很高精度。
表2 BP神经网络模型预测结果相对误差
Table 2 Prediction relative error of BP neural network model

3.2.3 ARIMA-BP组合模型的客流预测
分别选取ARIMA模型和BP神经网络模型的2008−08−01—2008−08−07的客流量预测数据进行组合预测,设置初始权重,根据式(12)和式(13)对两模型组合预测结果和真实值进行比较,计算方差并调整组合权重,直到得到输出方差最小所对应的组合权重分别为BP神经网络模型比例0.4,ARIMA模型比例0.6,于是输出权重值确定组合公式为
其中:为组合模型预测值;为BP神经网络模型预测值;为ARIMA模型预测值。得到预测效果如图4所示。
1—真实值;2—ARIMA模型预测值;3—BP神经网络模型预测值;4—组合模型预测值。
图4 预测效果对比图
Fig. 4 Comparison of prediction effect
表3所示为组合模型预测结果相对误差表。从表3可知:组合模型的相对误差几乎都在5%以下,具有高精度预测结果。
表3 组合模型预测结果相对误差表
Table 3 Prediction relative error of hybrid model

3.3 模型预测结果对比分析
由图4可见:组合模型误差相较于单一模型误差并不是整体偏低,平均绝对误差分数公式为
表4所示为绝对误差对比结果。
表4 绝对误差对比结果
Table 4 Comparison of absolute error %

从表4可知:ARIMA模型采用了变点分区的第8阶段数据作为样本进行预测,而BP神经网络模型预测则选取剔除节日影响因素较大的剩余数据作为样本进行预测,得到的结果显示ARIMA模型精度较高,BP神经网络模型次之,而两者的组合模型预测精度最高。组合模型虽然不能保证每次预测结果最为贴近实际值,但是相对于单一模型总体误差却最小,预测结果精度总体水平最高。
4 结论
1) 通过变点识别方法划分客流序列,结合变点分区状态下的ARIMA模型和全局网络学习的BP神经网络模型,构造了城市轨道日客运量的组合预测模型。
2) 划分了客流量变化模式区间,在不同的区间内,通过改变交通状态采用不同组合模型权重对数据进行拟合,对区间内数据更有针对性。由于同一模式区间具有类似的均值、方差等统计特征,因此同一模式区间预测比全局搜索预测更容易获得精度高的预测值。由于城轨客流受多方面因素的影响,在未来的研究中,仍需要通过现场勘查、历史信息回顾,将客流数据中隐含的未知信息进行挖掘,以便能使预测值更符合实际情况。
[1] 邱敦国. 一种基于双周期时间序列的短时交通流预测算法[J]. 四川大学学报(工程科学版), 2013, 45(5): 64−68. QIU Dunguo. A short-term traffic flow forecast algorithm based on double seasonal time series[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(5): 64−68.
[2] 姚向明, 赵鹏, 禹丹丹. 城市轨道交通网络短时客流OD估计模型[J]. 交通运输系统工程与信息, 2015, 15(2): 149−155. YAO Xiangming, ZHAO Peng, YU Dandan. Short-time passenger flow origin-destination estimation model for urban rail transit net-work[J]. Transportation Systems Engineering and Information, 2015, 15(2): 149−155.
[3] 毕湘利. 从效率角度谈城市轨道交通的规划、建设和运营[J]. 城市轨道交通研究, 2007, 10(10): 1−5. BI Xiangli. On efficient planning, construction and operation of URT[J]. Urban Mass Transit, 2007, 10(10): 1−5.
[4] 刘剑锋, 孙福亮, 柏赟, 等. 城市轨道交通乘客路径选择模型及算法[J]. 交通运输系统工程与信息, 2009, 9(2): 81−86. LIU Jianfeng, SUN Fuliang, BAI Yun, et al. Passenger flow route assignment model and algorithm for urban rail transit network[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(2): 81−86.
[5] 王玉萍. 城市轨道交通客流预测与分析方法[D]. 西安: 长安大学公路学院, 2011: 71−76. WANG Yuping. Study on urban rail transit passenger forecast and analysis[D]. Xi’an: Chang’an University. School of Highway, 2011: 71−76.
[6] 岳继光, 杨臻明, 孙强, 等. 区间时间序列的混合预测模型[J]. 控制与决策, 2013, 28(12): 1915−1920. YUE Jiguang, YANG Zhenming, SUN Qiang, et al. Hybrid model for interval-valued time series[J]. Control and Decision, 2013, 28(12): 1915−1920.
[7] 成诚, 杜豫川, 刘新. 考虑节假日效应的交通枢纽客流量预测模型[J]. 交通运输系统工程与信息, 2015, 15(5): 202−207. CHENG Cheng, DU Yuchuan, LIU Xin. A passenger volume prediction model of transportation hub considering holiday effects[J]. Transportation Systems Engineering and Information, 2015, 15(5): 202−207.
[8] 樊娜, 赵祥模, 戴明, 等. 短时交通流预测模型[J]. 交通运输工程学报, 2012, 12(4): 114−119. FAN Na, ZHAO Xiangmo, DAI Ming, et al. Short-term traffic flow prediction model[J]. Journal of Traffic and Transportation Engineering, 2012, 12(4): 114−119.
[9] 王维强, 牛振东, 曹玉娟, 等. 基于ARMA−TS−GARCH有限混合模型的交通数据分析[J]. 中南大学学报(自然科学版), 2010, 41(5): 1860−1864. WANG Weiqiang, NIU Zhendong, CAO Yujuan, et al. Analysis of traffic data based on ARMA−TS−GARCH finite mixture model[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1860−1864.
[10] 郭义荣, 张晓栋, 董宝田, 等. 基于模糊理论的交通状态快速识别与跃迁转变方法[J]. 中南大学学报(自然科学版), 2013(S1): 1−5. GUO Yirong, ZHANG Xiaodong, DONG Baotian, et al. Traffic state of rapid identification and transition shift method based on fuzzy theory[J]. Journal of Central South University (Science and Technology), 2013(S1): 1−5.
[11] 何九冉, 四兵锋. EMD−RBF组合模型在城市轨道交通客流预测中的应用[J]. 铁道运输与经济, 2014, 36(10): 87−92. HE Jiuran, SI Bingfeng. Application of EMD−RBF combined model on passenger flow forecast of urban rail transit[J]. Rail Way Transport and Economy, 2014, 36(10): 87−92.
[12] 何九冉. 城市轨道交通客流统计特征分析及组合预测方法实证研究[D]. 北京: 北京交通大学交通运输学院, 2013: 37−43. HE Jiuran. Urban railway traffic passenger flow statistical characteristics analysis and empirical study on the combination forecast method[D]. Beijing: Beijing Jiaotong University. School of Traffic and Transportation, 2013: 37−43.
[13] 杨志勇. 基于灰色系统和神经网络的实时交通量预测组合模型研究[J]. 公路, 2015, 60(3): 104−108. YANG Zhiyong. Research on combined model for real-time traffic volume prediction based on grey system and neural network[J]. Highway, 2015, 60(3): 104−108.
[14] 刘岩. 城市轨道交通断面客流短时预测[D]. 南京: 东南大学交通学院, 2014: 12−20. LIU Yan. Urban rail transit short-term sectional passenger flow forecasting[D]. Nanjing: Southeast University. School of Transportation, 2014: 12−20.
[15] 马超群. 城市轨道交通客流特征与规律分析[J]. 铁道运输与经济, 2015, 37(6): 85−91. MA Chaoqun. Analysis on characteristics and principle of passenger flow of urban rail transit[J]. Rail Way Transport and Economy, 2015, 37(6): 85−91.
[16] 四兵锋, 何九冉, 任华玲, 等. 基于时序特征的城市轨道交通客流预测[J]. 北京交通大学学报, 2014, 38(3): 1−6. SI Bingfeng, HE Jiuran, REN Hualing, et al. Urban railway traffic passenger flow forecast based on the timing characteristics[J]. Journal of Beijing Jiaotong University, 2014, 38(3): 1−6.
[17] 董升伟. 基于改进BP神经网络的轨道交通短时客流预测方法研究[D]. 北京: 北京交通大学交通运输学院, 2013: 27−33. DONG Shengwei. The research of short-time passenger flow forecasting based on improved BP neural network in urban rail transit[D]. Beijing: Beijing Jiaotong University. School of Traffic and Transportation, 2013: 27−33.
[18] 常刚, 张毅, 姚丹亚. 基于时空依赖性的区域路网短时交通流预测模型[J]. 清华大学学报(自然科学版), 2013, 53(2): 215−221. CHANG Gang, ZHANG Yi, YAO Danya. Short-term traffic flow forecasting model for regional road network based on spatial-temporal dependency[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(2): 215−221.
[19] 王建, 邓卫, 赵金宝. 基于贝叶斯网络多方法组合的短时交通流量预测[J]. 交通运输系统工程与信息, 2011, 11(4): 147−153. WANG Jian, DENG Wei, ZHAO Jinbao. Short-term freeway traffic flow prediction based on multiple method-s with bayesian net-work[J]. Transportation Systems Engineering and Information, 2011, 11(4): 147−153.
[20] 杨丽, 杨德明. 深圳市城市轨道交通网络化客流变化研究[J]. 现代城市轨道交通, 2012(6): 72−75. YANG Li, YANG Deming. Study on passenger flow change in shenzhen urban rail transit network[J]. Modern Urban Transit, 2012(6): 72−75.
(编辑 罗金花)
A forecasting model for urban rail transit passenger flow based on change-point detection method
ZHU Guangyu1, WANG Yuchen1, ZHANG Peng2, AI Bo3, BIAN Liqin4
(1. MOE Key Laboratory for Transportation Complex Systems Theory and Technology,Beijing Jiaotong University, Beijing 100044, China;2. Beijing Municipality Key Laboratory of Urban Traffic Operation Simulation and Decision Support,Beijing Transportation Research Center, Beijing 100073, China;3. State Key Laboratory of Rail Traffic Control and Safety, Beijing 100044, China;4. Jinan RETURNS Railway Signalling and Communication Co., Ltd., Jinan 250013, China)
According to the urban rail transit development changes, and characteristics of their respective changes in passenger flow were analyzed. Based on the method of the change-point detection, the variation of the passenger flow in rail transit was classified, and the influence factors on the variation of the passenger flow pattern were analyzed. Changing the weights of variable parameters ARIMA model in the interval of different modes and the BP neural network model, a combined forecasting model of urban transit passenger flow during the network operation was proposed. The validity and accuracy of this model was proved by utilizing the real data of urban rail transit. The results show that prediction accuracy of the same pattern is higher than global searching, and combined model prediction results are better than the single model’s.
urban rail transit; passenger flow prediction; change-point detection method;hybrid model; auto-regressive and moving average model
10.11817/j.issn.1672-7207.2016.06.045
U231
A
1672−7207(2016)06−2153−07
2016−01−24;
2016−03−24
国家自然科学基金面上资助项目(61572069);中央高校基本科研业务费(2014JBM211);系统控制与信息处理教育部重点实验室开放课题(Scip201507);河北省交通运输厅科技项目(A0201-150505);北京城市交通协同创新中心项目(T14L00850)(Project (61572069) supported by Supported by the National Natural Science Foundation of China; Project(2014JBM211) supported by the Fundamental Research Funds for the Central Universities; Project(Scip201507) supported by the Key Laboratory of System Control and Information Processing of Ministry of Education; Project(A0201-150505) supported by the Science and Technology Project of Transportation Department of Hebei Province; Project(T14L00850) supported by Center of Cooperative Innovation for Beijing Metropolitan Transportation)
朱广宇,博士,副教授,从事智能交通研究;E-mail:gyzhu@bjtu.edu.cn

