相变对两相区连续退火带钢温度和屈曲变形的影响
吴雯,米振莉,苏岚,孙蓟泉,陈银莉
相变对两相区连续退火带钢温度和屈曲变形的影响
吴雯,米振莉,苏岚,孙蓟泉,陈银莉
(北京科技大学冶金工程研究院,北京,100083)
以低碳铝镇静钢对研究对象,利用有限元数值模拟方法,分别对连退炉内加热段和缓冷段中带钢相变对带钢温度分布和带钢屈曲变形的影响进行研究。研究结果表明:对于在两相区进行连续退火热处理的钢种,在加热段,相变能有效抑制由带钢热应力引起的横向诱导压应力的增大,并且降低带钢温度和横向温差,从而抑制带钢发生屈曲变形,在760~820 ℃退火时,相变对带钢屈曲变形的抑制作用随着退火温度的升高先增大再减小;在缓冷段,相变减弱了带钢热应力减小横向诱导压应力的作用,并且升高带钢温度,从而使带钢容易发生屈曲变形;退火温度越高,发生相变的带钢越容易屈曲变形。
连续退火带钢;相变;温度;屈曲;有限元法
带钢连续退火生产线具有生产效率高、生产成本低、产品质量好、产品品种多样化等优点,已成为生产高质量冷轧带钢产品最重要的加工工艺之一。但带钢在连续退火炉内普遍存在着带钢瓢曲的问题,大大降低了生产线的经济效益。国内外众多学者分别通过有限元模拟[1−6]、解析法[7−10]和实验法[10−13]等方法分析了带钢瓢曲的机理及影响因素,在研究带钢宽度和厚度、导向辊辊形、带钢原始板形、宽度方向温差、炉内张力和摩擦等对带钢瓢曲的影响方面取得了一定成果。但在研究带钢瓢曲时,很少考虑到连退过程中带钢本身组织与物理性能等的变化对瓢曲的影响。连退炉内带钢的瓢曲实质上是薄板的屈曲和后屈曲变形。在实际生产中,有许多钢种都属于两相区退火工艺。由于铁素体F和奥氏体A之间的转变伴随着材料物理性能的突变、体积的改变和相变潜热的释放,这些都将会给带钢屈曲和后屈曲变形带来一定影响。因此,本文作者以低碳铝镇静钢为研究对象,针对连退过程中由带钢横向诱导压应力引起的屈曲变形,建立带钢相变−温度−屈曲间接耦合有限元计算模型,研究相变对带钢温度场和屈曲变形行为的影响。
1 计算模型的建立
1.1 连退带钢传热模型
对于带钢在连退处理中热传导过程,可以忽略长度方向的热量流动,因此采用带钢单元温度跟踪模型计算带钢温度场,控制方程为
式中:和为带钢厚度、宽度方向坐标;为时间;为时刻带钢上(,)点的温度;为带钢热导率;为带钢密度;为带钢比热容;为材料内部热源 密度。
由于带钢在连退炉内运行时不同位置的带钢热传导边界条件不同,因此,对不同位置的带钢采用不同的边界条件进行计算。在加热段主要考虑了辐射管加热、炉气对流传热和带钢与炉辊的接触传热;在缓冷段主要考虑了喷射气体冷却、炉气对流传热和带钢与炉辊的接触传热。
控制方程中材料内热源相为相变潜热,密度为
式中:Δ为相变产生的热量;Δ为Δ时间内转变的相体积分数。
1.2 相变动力学模型
固态相变通常采用KJMA(Kolmogorov−Johnson− Mehl−Avrami)公式来描述:
式中:为转变的体积分数;和分别为与钢的成分及温度有关的常数。本文采用DIL805A热膨胀仪进行相变数据测量。
1.2.1 加热过程带钢相变模型
由于F→A相变孕育期极短难以准确测定其等温奥氏体化动力学曲线,因此本文中F→A相变采用连续相变动力学曲线进行描述[14−18]。由测得奥氏体化加热试验膨胀曲线,相变开始温度为740 ℃,根据杠杆定理计算不同时刻奥氏体体积分数,由式(3)可得:
1.2.2 冷却过程带钢相变模型
缓冷段带钢发生A→F转变,根据可加性法则,将连续相变过程用一系列微小等温相变过程之和进行描述。实验测得奥氏体转变TTT(time,temperature,transformation)曲线如图2所示,由式(5)计算得到不同温度下的和。
式中:s和e分别为对应某一温度下2个等温时间s和e的转变量。
1.3 有限元模型
1.3.1 几何模型
对实际生产线进行适当的抽象简化,只考虑1段带钢和1个炉辊,由于带钢尺寸、炉辊和炉内工况均关于带钢宽度中心线对称,因此仅取带钢宽度的一半进行建模。
炉辊选取单锥度辊,尺寸如图3所示。由于炉辊刚度较带钢的大,形状简单,而且本文不考虑炉辊的变形,因此采用解析刚体建模。

单位:mm
带钢和炉辊位置示意图如图4所示,带钢两截断边平直段′和′长度分别为10 m和2 m,带宽 1.6 m,带厚0.6 mm,单元类型选用八节点曲面薄壳单元。有限元计算模型如图5所示。

单位:mm

图5 带钢屈曲分析有限元模型
1.3.2 带钢的物性参数
带钢密度为7 859 kg/m3,热导率()、比定压热容(c)和线膨胀系数取两相的线性平均值。
式中:表示各相相应的物理量;表示各相体积比。线膨胀系数和相变膨胀系数由热膨胀仪测量数据确定。以上各物理量与温度的关系如表1所示。
表1 物理参数和温度的关系
Table 1 Relationship between physical parameters and temperature

采用自由衰减法测得带钢高温弹性模量如图6所示。采用CMT5105拉伸机测得高温屈服强度如图7所示,材料的泊松比为0.28。

图6 带钢弹性模量与温度的关系

图7 带钢屈服强度
1.3.3 计算工况和边界条件
某工厂低碳铝镇静钢退火温度为790 ℃的连退线加热段、均热段、缓冷段温度和各段炉内张力设置如表2所示。对于连续退火热处理的低碳铝镇静钢,在加热段、均热段和缓冷段都会存在带钢相变,因此本文选择加热段和缓冷段的带钢为研究对象,基于现场工艺,为了研究带钢相变对屈曲临界载荷的影响,选用退火温度为760,790和820 ℃,对带钢在加热过程和缓冷过程中,分别考虑相变影响和不考虑相变影响2种情况下的模型进行计算并加以对比,计算工况如表3所示。
表2 某厂低碳铝镇静钢790 ℃连续退火工艺
Table 2 Continuous annealing process at 790 ℃ of low-carbon Al-killed steel

表3 计算工况
Table 3 Calculation condition

计算过程为:
1) 分别对加热段2~3号和缓冷段带钢进行温度场计算和温度−相变耦合计算,得到带钢宽度方向的温度和相变量分布。边界条件:炉辊尺寸如图3所示,炉辊间平直段长度为20 m,带速260 m/min,加热段2~3号总长446 m,缓冷段总长84 m。
2) 将第1)步得到的带宽方向温度和相变量分布读入有限元模型中,从而将热应力和相变应力加入带钢应力场中,而后分别对考虑相变和不考虑相变两种模型中的带钢进行屈曲分析,得到带钢屈曲模态,并通过提取特征值计算不同工况下带钢的屈曲临界载荷。
边界条件:炉辊固定不动,带钢纵向对称线上的节点施加带宽方向的对称约束,图4所示两截断边′和′施加带宽和带厚方向的旋转约束,加热段′截断边施加张力为6.5 kN,缓冷段施加张力为10.2 kN,′截断边施加带长方向位移约束。
2 计算结果与分析
2.1 带钢相变−温度耦合计算结果
2.1.1 相变对带钢温度的影响
加热和缓冷过程中带钢宽度中心的温度和相变量变化分别如图8和图9所示,其中:A和F分别为A和F的体积分数。在加热段,带钢温度达到F→A相变温度后,会发生F→A转变。相变伴随着相变潜热的释放,从而影响带钢温度,由于F→A相变过程吸收热量,A→F相变过程释放热量,因此,在加热段,考虑相变的带钢温度比不考虑相变的情况下低,而缓冷段正相反。可以看出:相变量越大,带钢温度升高或降低的程度越大,而且在缓冷段的前半段,带钢相变已经完成。

1—760 ℃无相变温度;2—790 ℃无相变温度;3—820 ℃无相变温度;4—760 ℃有相变温度;5—790 ℃有相变温度;6—820 ℃有相变温度;7—760 ℃相变量;8—790 ℃相变量;9—820 ℃相变量。

1—760 ℃无相变温度;2—790 ℃无相变温度;3—820 ℃无相变温度;4—760 ℃有相变温度;5—790 ℃有相变温度;6—820 ℃有相变温度;7—760 ℃相变量;8—790 ℃相变量;9—820 ℃相变量。
2.1.2 相变对带钢横向温差的影响
连退内不均匀的热边界条件会引起带钢横向温差,带钢横向温差会导致带钢相变量的差异。记带钢横向温差为Δ带钢中心温度与带钢边缘温度之差,横向相变量差为Δ为带钢中心相变量与带钢边缘相变量之差。
加热段发生相变后带钢横向温差Δ和奥氏体体积分数差ΔA随时间变化如图10所示。在加热段,由于带钢中部温度高于边部,中部带钢先于边部带钢达到F→A相变开始温度,使得带钢宽度方向存在相变量差。由式(3)可知:当相变开始时间差相等时,相变量差随着相变时间的增长先增大再减小,直至相变结束;而对于不同的相变开始时间差,时间差越大,相同的相变时间内相变量差越大。对于不同退火温度的带钢,退火温度越高,带钢升温速度越快,相变开始时间越早,而相变开始时间的差值越小。在相变开始时间差和相变时间的综合作用下,加热段40~80 s内表现为退火温度越高,相变量差越大;随着相变的进行,不同退火温度下的相变量差逐渐趋于其最大值,因此到加热段结束时,820 ℃的相变量差小于790 ℃的相变量差,790 ℃和760 ℃相变量差的差距也减小。

1—760 ℃无相变温差;2—790 ℃无相变温差;3—820 ℃无相变温差;4—760 ℃有相变温差;5—790 ℃有相变温差;6—820 ℃有相变温差;7—760 ℃相变量;8—790 ℃相变量;9—820 ℃相变量。
相变量差的存在也会进一步影响带钢温差,由式(2)可知:带钢中部和边部相变潜热差的绝对值和相变量差曲线具有相同的变化趋势和规律,由于F→A相变过程吸收热量,相变潜热差会随着相变的进行会先减小再增大,而且相变开始时间差越大,相变潜热差的最小值越小。所以,在加热段结束时,760 ℃退火的带钢相变使横向温差减小幅度最大,其次为790 ℃,820 ℃时最小。
图11所示为缓冷段第1道次带钢横向温差Δ和铁素体体积分数差ΔF随时间变化。在缓冷段,带钢中部温度低于边部,使带钢宽度方向相变量存在差异。对于退火温度为760 ℃的带钢,由于带钢发生相变的温度位于C曲线拐点以下,温度越低,相变速度越小,所以横向相变量差会出现负值;790 ℃和820 ℃退火的带钢发生A→F相变的温度位于C曲线拐点以上,所以带钢中部相变量大于边部。与加热段类似,相变量差存在最大值或最小值,可以看出,在缓冷段第1道次,790 ℃退火的带钢相变量差已经达到最大值。

1—760 ℃无相变温差;2—790 ℃无相变温差;3—820 ℃无相变温差;4—760 ℃有相变温差;5—790 ℃有相变温差;6—820 ℃有相变温差;7—760 ℃相变量;8—790 ℃相变量;9—820 ℃相变量。
与加热段同理,相变量差会影响带钢温差,760 ℃退火带钢由于负的横向相变量差会带钢横向温差绝对值加大,而790 ℃和820 ℃退火的带钢不均匀的相变则会减小带钢横向温度差异。但由于发生A→F相变时带钢过冷度较大,且位于C曲线拐点附近,带钢相变速度较快,使得带钢横向相变量差很小,因此对带钢横向温差的影响并不明显。
2.2 相变对带钢屈曲临界载荷的影响
为了研究相变对横向压应力引起的带钢屈曲变形的影响,本文只分析加热段结束和缓冷段第1道次结束时,考虑相变和不考虑相变两种模型的带钢屈曲临界载荷。
图12和图13所示分别为790 ℃连退加热段和缓冷段,考虑相变和不考虑相变情况下得到的带钢屈曲模态(放大200倍)。表4所示为不同工况下带钢屈曲临界载荷的计算结果。从表4可以看出:在加热段,对于不考虑相变的带钢,在带钢温度、热应力和带钢张力的共同作用下,带钢临界载荷比较小,很容易发生屈曲变形;当考虑带钢相变时,带钢屈曲临界载荷明显增大,即相变可以抑制带钢发生屈曲变形,对比同一退火温度下考虑相变和不考虑相变的屈曲临界载荷可知,相变对带钢屈曲的抑制作用随着退火温度的升高先增大再减小。在缓冷段,对于不考虑相变的带钢,退火温度越高,屈曲临界载荷越小,带钢越容易发生屈曲变形。当考虑带钢相变时,屈曲临界载荷有所下降,即相变对带钢的屈曲变形有促进作用,而且在760~820 ℃退火时,退火温度越高,相变对带钢屈曲变形的促进作用越明显。

(a) 不考虑相变;(b) 考虑相变
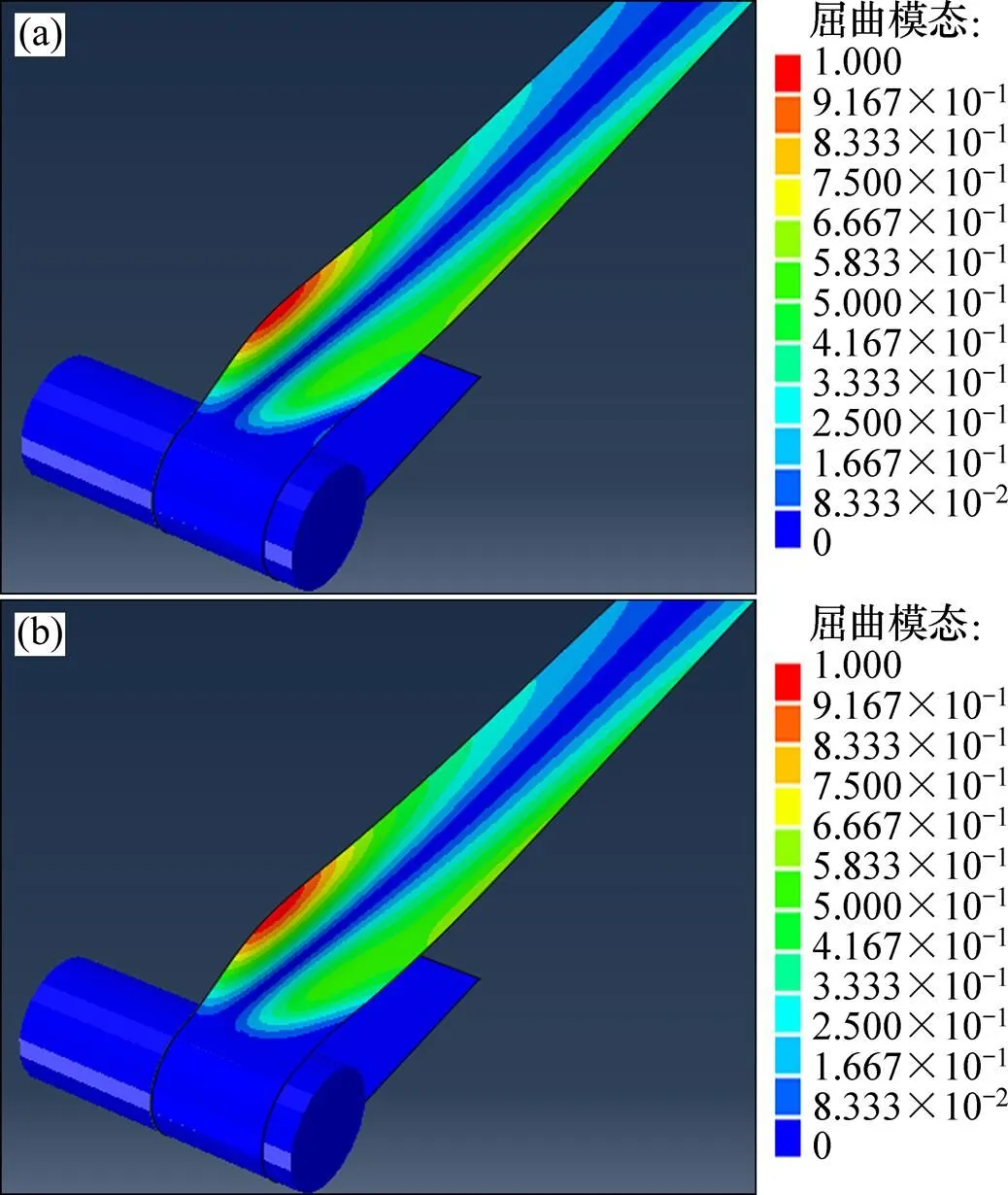
(a) 不考虑相变;(b) 考虑相变
表4 不同工况带钢屈曲临界载荷
Table 4 Critical buckling stress of strip in different calculation condition MPa

在本文的研究范围内,带钢横向温差、横向相变量差和带钢温度均会对带钢临界屈曲载荷造成一定影响。
在连退炉内,由于炉辊锥度的影响,施加在带钢上的张力会使靠近炉辊区域的带钢宽度方向上应力分布不均匀,在带钢宽度的中间部分会存在横向压应力,导致带钢容易发生屈曲变形。记
1—760 ℃无相变;2—790 ℃无相变;3—820 ℃无相变;4—760 ℃有相变;5—790 ℃有相变;6—820 ℃有相变。
图14 加热段带钢膨胀量的横向分布
Fig. 14 Expansion transverse distribution of strip in heating section
本质上而言,热应力的产生是热膨胀不均匀产生的,是结构不同部分温度变化不同时原子间距变化不同而产生的内应力。对于加热段考虑相变影响的带钢而言,带钢在发生F→A相变时,内部晶体结构由体心立方向更为密排的面心立方转变,致密度增大,因此,相变可以有效减小由于温度升高导致的原子间距的增大,同时,相变也可以减小带钢横向温差,使得带钢膨胀量沿横向的分布趋于均匀化,从而减小带钢横向温差引起的内应力。从图14还可以看出:当加热段炉温为790 ℃时,带钢膨胀分布最均匀,故而790 ℃对应的屈曲临界载荷最大,其次为760 ℃,820 ℃退火时屈曲临界载荷最大。即790 ℃退火时相变对带钢屈曲的抑制作用最明显,760 ℃其次,820 ℃退火时相变对带钢屈曲的抑制作用最弱。
对于位于缓冷段的带钢,当不考虑带钢相变时,与加热段相反,带钢温度中间低两边高,热应力为带钢中部受拉,这可以在一定程度上减小带钢横向压应力,有利于抑制带钢的屈曲变形。图15所示为缓冷段带钢膨胀量的横向分布。从图15可以看出:不考虑相变时,退火温度越高,膨胀量不均匀的程度高一些,对屈曲的抑制作用应该更大,但计算结果表明:退火温度越高,带钢屈曲临界载荷越小,因此可以推断此时影响带钢屈曲变形的主要因素是温度。当考虑缓冷段带钢相变的影响时,A→F相变为体积膨胀过程,因此对带钢内应力的作用与加热段相反,而且,发生相变后带钢的温度显著升高,使得带钢容易发生屈曲变形。对比同一退火温度下的相变膨胀分布可以看出:退火温度越高,相变使带钢膨胀量分布趋于均匀的作用越明显,即相变对带钢屈曲变形的促进作用越明显。
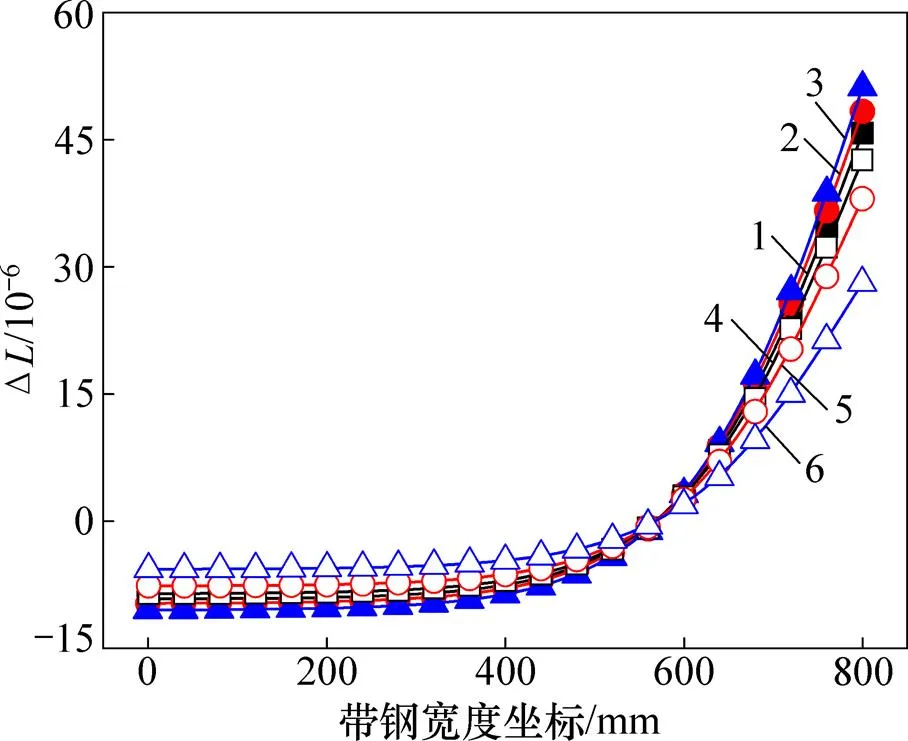
1—760 ℃无相变;2—790 ℃无相变;3—820 ℃无相变;4—760 ℃有相变;5—790 ℃有相变;6—820 ℃有相变。
实际生产中发现,有时带钢在经过均热段后并未发生瓢曲,而在冷却时却出现瓢曲现象,这很难用传统的瓢曲理论进行解释。本文在带钢屈曲模型中引入了相变的影响,计算结果表明,加热段带钢的相变有利于抑制其屈曲变形,而在缓冷段发生相变的带钢更容易发生屈曲变形,与实际情况相符。
3 结论
1) 在两相区进行连续退火热处理的钢种,相变可以降低加热段的带钢温度和横向温差,在本文研究范围内,退火温度越低,相变对带钢横向温差影响越明显;缓冷段相变使带钢温度升高,760 ℃退火时,横向温差基本不变,790 ℃和820 ℃相变使横向温差小幅度减小。
2) 对于在两相区连续退火的钢种,在连退炉加热段,相变能有效抑制由带钢热应力引起的横向诱导压应力的增大,并且降低带钢温度,从而抑制带钢发生屈曲变形;在760~820 ℃退火时,相变对带钢屈曲变形的抑制作用随着退火温度的升高先增大再减小。
3) 对于在两相区连续退火的钢种,在连退炉缓冷段,相变减弱了带钢热应力减小横向诱导压应力的作用,并且升高带钢温度,从而使带钢容易发生屈曲变形;在760~820 ℃退火时,退火温度越高,发生相变的带钢越容易屈曲变形。
[1] 唐荻, 杨静, 苏岚, 等. 连退炉内炉辊热变形对带钢瓢曲变形的影响[J]. 中南大学学报(自然科学版), 2012, 43(5): 1724−1731.TANG Di, YANG Jing, SU Lan, et al. Influence of roller thermal deformation on strip buckling in continuous annealing furnace[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1724−1731.
[2] CHEN T T, HO C H, LIN J C, et al. 3-D temperature and stress distributions of strip in preheating furnace of continuous annealing line[J]. Applied Thermal Engineering, 2010, 30(8/9): 1047−1057.
[3] JACQUES N, ELIAS A, POTIER−FERRY M, et al. Buckling and wrinkling during strip conveying in processing lines[J]. Journal of Materials Processing Technology, 2007, 190(1): 33−40.
[4] ZHANG Y, YANG Q, HE A R, et al. Deviation prevention ability of rollers in continuous annealing furnace and application[J]. Journal of Iron and Steel Research International, 2012, 19(12): 8−13.
[5] QIN J, ZHANG Q D, HUANG K F. Oblique and herringbone buckling analysis of steel strip by spline FEM[J]. Journal of Iron and Steel Research International, 2011, 18(9): 21−26.
[6] KANG Z W, CHEN T C. Three-dimensional temperature distributions of strip in continuous annealing line[J]. Applied Thermal Engineering, 2013, 58(1/2): 241−251.
[7] 刘顺明, 尹显东, 郑晓飞, 等. 退火炉内带钢拉伸失稳与屈曲失稳分析[J]. 轧钢, 2013, 30(6): 22−24.LIU Shunming, YIN Xiandong, ZHENG Xiaofei, et al. Analysis of tensile instability and buckling instability of strip in the furnace of continuous annealing line[J]. Steel Rolling, 2013, 30(6): 22−24.
[8] 卢兴福, 张清东, 张晓峰. 薄宽带钢翘曲变形行为解析研究[C]//第九届中国钢铁年会. 北京, 2013: 1−6.LU Xingfu, ZHANG Qingdong, ZHANG Xiaofeng. Analysis of warp deformation for thin and wide strip[C]//Proceedings of the 9th China Iron & Steel Annual Meeting. Beijing, 2013: 1−6.
[9] BRIGHENTI R. Buckling of cracked thin-plates under tension or compression[J]. Thin-Walled Structures, 2005, 43(2): 209−224.
[10] 张清东, 常铁柱, 戴江波. 带钢高温态横向瓢曲的理论与试验[J]. 机械工程学报, 2008, 44(8): 219−226.ZHANG Qingdong, CHANG Tiezhu, DAI Jiangbo. Theory and experiment of the strip transverse buckling under high temperature[J]. Chinese Journal of Mechanical Engineering, 2008, 44(8): 219−226.
[11] KASEDA Y, MASUI T. Control of buckling and crossbow in strip processing lines[J]. Physical Review D, 1994, 71(11): 174−176.
[12] SASAKI T, HIRA T, ABE H, et al. Control of strip buckling and snaking in continuous annealing furnace[J]. Kawasaki Steel Technical Report, 1984, 16(1): 37−45.
[13] MATOBA T, ATAKA M, AOKI I, et al. Effect of roll crown on heat buckling in continuous annealing and processing lines[J]. Journal of the Iron and Steel Institute of Japan-Tetsu to Hagane, 1994, 80(8): 641−646.
[14] 陈睿恺, 顾剑锋, 韩利战, 等. 30Cr2Ni4MoV钢的奥氏体化动力学[J]. 材料热处理学报, 2013, 34(1): 170−174.CHEN Ruikai, GU Jianfeng, HAN Lizhan, et al. Austenitization kinetics of 30Cr2Ni4MoV steel[J]. Transactions of Material and Heat Treatment, 2013, 34(1): 170−174.
[15] 张芳. 非等温奥氏体化动力学模型[J]. 金属热处理, 2013, 38(8): 6−9.ZHANG Fang. Kinetics model of non-isothermal austenite formation[J]. Heat Treatment of Metals, 2013, 38(8): 6−9.
[16] SAN−MARTÍN D, RIVERA−DÍAZ−DEL−CASTILLO P E J, GARCÍA−DE−ANDRÉS C. In situ study of austenite formation by dilatometry in a low carbon microalloyed steel[J]. Scripta Materialia, 2008, 58(10): 926−929.
[17] LI Dan, MIN Yongan, WU Xiaochun. Calculation of austenite formation kinetics of copper-bearing steel during continuous heating[J]. Journal of Iron and Steel Research International, 2010, 17(11): 62−66.
[18] OLIVEIRA F L G, ANDRADE M S, COTA A B. Kinetics of austenite formation during continuous heating in a low carbon steel[J]. Materials Characterization, 2007, 58(3): 256−261.
(编辑 赵俊)
Effect of phase transformation on temperature and buckling of continuous annealing strip in two-phase region
WU Wen, MI Zhenli, SU Lan, SUN Jiquan, CHEN Yinli
(Institute of Metallurgy Engineering, University of Science and Technology Beijing, Beijing 100083, China)
Low-carbon Al-killed steel was selected and finite element method (FEM) was used to investigate the influence of phase transformation on strip temperature distribution and buckling in the heating and slow cooling sections of the continuous annealing furnace. The results show that in the heating section, phase transformation can inhibit the increase of transverse compressive stress caused by thermal stress and reduce temperature and transverse temperature difference of strip effectively, and thus it is helpful to prevent the strip buckling. Inhibition of phase transformation on strip buckling firstly increases and then decreases when annealed at 760−820 ℃. In the slow cooling section, phase transformation weakens the decrease of transverse compressive stress caused by thermal stress and reduces temperature of strip, which promotes the probability of strip buckling. Strip buckling is more likely to occur at higher annealing temperature.
continuous annealing strip; phase transformation; temperature; buckling; FEM
10.11817/j.issn.1672-7207.2016.06.003
TG156.2
A
1672−7207(2016)06−1835−08
2015−06−04;
2015−09−11
国家自然科学基金资助项目(51104017)(Project(51104017) supported by the National Natural Science Foundation of China)
苏岚,博士,工程师,从事材料加工工艺与控制研究;E-mail:sulan@ustb.edu.cn

