蒸汽吞吐割缝筛管水平井井筒入流规律
陈会娟,李明忠,刘春苗,李威威,张艳玉
蒸汽吞吐割缝筛管水平井井筒入流规律
陈会娟1,李明忠1,刘春苗2,李威威1,张艳玉1
(1. 中国石油大学石油工程学院,山东青岛,266580;2. 中海油能源发展工程技术公司钻采工程研究所,天津,300452)
基于割缝筛管完井水平井实际管柱结构,考虑流体在水平井筒内的变质量流特性,建立蒸汽吞吐水平井注入和产出过程中井筒与储层耦合数学模型,并采用迭代法对其进行求解;将其计算结果与数值模拟软件计算结果进行对比,验证模型的准确性;以此为基础,系统研究蒸汽吞吐注入和生产过程中水平井井筒入流规律。研究结果表明:蒸汽吞吐注入过程中,井筒压力与温度从水平井跟端到趾端逐渐降低,但降低幅度并不显著;蒸汽入流剖面与地层温度沿井筒呈凹型分布,且随着时间的增加,蒸汽入流剖面与地层温度沿井筒的非均质性增加;蒸汽吞吐生产过程中,井筒压力从水平井趾端到跟端依次降低,而井筒温度却先降低后稍微增加;原油与地层水入流剖面沿井筒呈凹型分布。
割缝筛管;水平井;蒸汽吞吐;井筒压力;井筒温度;入流剖面
割缝筛管完井水平井因其独特的优势在稠油油藏蒸汽吞吐开采中得到广泛应用[1−3],并获得较好的经济效益。但在水平井蒸汽吞吐开采过程中,流体在井筒内除沿水平方向流动外,沿径向与油藏之间亦存在质量与能量交换,致使水平井注入和产出剖面沿井筒分布并不均匀,影响蒸汽吞吐开发效果;因此,有必要对蒸汽吞吐水平井井筒入流规律进行研究。目前,国内学者[4−6]主要针对蒸汽吞吐注入过程中水平井筒内蒸汽传热与传质规律进行了研究,对蒸汽吞吐生产阶段的研究相对较少,并且在其研究中均未考虑储层内压力与温度的变化;国外学者建立了热采水平井井筒与储层耦合的离散井模型[7−8]、多段井模型[9−10]和灵活井模型[11],但离散井模型中水平井筒内的管流等效为流体在多孔介质中的渗流,热采多段井模型未考虑多相流体之间的滑脱,灵活井模型则采用简单的机理模型计算水平井筒压降,且上述模型中水平井筒均假设为理想的裸眼完井,不能反映流体在实际割缝筛管水平井筒内的流动特征。因此,本文作者基于割缝筛管完井水平井实际管柱结构,考虑注入蒸汽及产出液在水平井筒内的变质量流特性,建立蒸汽吞吐水平井注入和产出过程中井筒与储层耦合数学模型;以此为基础,系统研究蒸汽吞吐水平井井筒入流规律,以便为现场科学、合理地指导水平井蒸汽吞吐开发提供理论依据。
1 数学模型的建立
1.1 基本假设
模型基本假设条件如下:
1) 油藏内存在油、汽、水三相流动,且流动满足达西定律;2) 油藏内渗流为非等温渗流,温度影响油、汽、水黏度及三相相对渗透率;3) 流动过程中的热量通过传导和对流的方式实现热传递;4) 对于油藏中的任一微元体,瞬间便可建立相平衡及热平衡;5) 考虑重力和毛管力的影响。
1.2 地层内传热与传质数学模型的建立
地层内传热与传质模型包括油、汽、水三相的质量守恒方程、能量守恒方程及蒸汽相热平衡方程,具体表达式如下。
1) 质量守恒方程:
对于油相,
对于水相,
对于蒸汽相,
式中:下标o,w和g分别代表油相、水相和蒸汽相;为密度,kg/m3;为单位转换系数;为储层渗透率,10−3µm2;ro,rw和rg分别为油相、水相和蒸汽相相对渗透率;为黏度,Pa·s;为压力,Pa;为重力加速度,m/s2;为标高,m;o,w和g分别为地层条件下,单位时间单位体积储层中注入或采出的油相、水相和蒸汽相体积,m3/(m3·s);c为地层条件下,单位时间单位体积储层中蒸汽凝结成水的质量,kg/(m3·s);为时间,s;为饱和度;为储层孔隙度。
2) 能量守恒方程:

(4)
式中:R为油层导热系数,W/(m·℃);为油藏温度,℃;H为相流体的焓,J/kg;h为单位时间单位体积储层中注入或产出的能量,J/(m3·s);loss为单位时间内,单位体积储层向顶底层散失的能量,J/(m3·s);R为岩石密度,kg/m3;R为油层岩石比热容,J/(kg·℃);U为第相流体内能,J/kg。
3) 蒸汽相热平衡方程:
式中:s为饱和蒸汽压力,Pa;s为饱和蒸汽温度,℃。
4) 辅助方程。
饱和度方程:
毛管力方程:
1.3 井筒内传热与传质数学模型的建立
流体在水平井筒内的流动为变质量流,但在蒸汽吞吐注入阶段,水平井筒内为湿蒸汽混合物的气液两相流,而在蒸汽吞吐生产阶段,水平井筒内为油和水的两相流;因此,需分别建立其井筒内传热与传质数学模型。
将长度为的割缝筛管完井水平井均分为个连续微元段,假设每一微元段包含一定数量的割缝,在同一微元段上流体从井筒(地层)沿割缝等质量均匀流入地层(井筒),而不同微元段流体流量不等。在割缝筛管完井水平井筒任意位置取一微元段,微元段长度为d,微元段内割缝排数为gf,割缝单元长度为u,则gf=d/u,如图1所示。

(a) 蒸汽吞吐注入阶段;(b) 蒸汽吞吐产出阶段
1.3.1 蒸汽吞吐注入阶段
对于蒸汽吞吐注入阶段,由质量守恒、能量守恒和动量定理可得:
蒸汽在水平井筒中流动时,其气相的体积流量要远大于液相的体积流量,因此可看做理想气体[15−16],故

(12)
式中:wf为井筒内蒸汽温度,℃。
同时有辅助方程:

(13)
将式(12)和(13)分别代入式(10)和式(11),整理可得蒸汽干度和压力沿井筒分布计算表达式:
(15)
由式(14)和式(15)即可求得蒸汽吞吐注入阶段水平井任意位置处蒸汽压力和干度。根据式(5),即可求得水平井筒任意位置处蒸汽温度分布。
1.3.2 蒸汽吞吐生产阶段
对于蒸汽吞吐生产阶段,井筒内流体为油和水混合物,其质量守恒方程、能量守恒方程和动量守恒方程表达式如下[17]:
依据热力学原理,油水两相混合物的焓可以表示成压力和温度的函数,即,故

(19)
式中:oJ和wJ分别为油和水的焦耳汤姆逊系数,℃/Pa;o和w分别为油和水的比热容,J/(kg·℃)。

(20)
将式(19)和(20)带入式(17)和(18),整理可得井筒内压力和温度表达式:
(22)
其中:

;

T为流体热膨胀系数,1/℃;为流体由井筒向地层传热热阻,m·℃/W。
由式(21)和式(22)即可求得蒸汽吞吐生产阶段水平井任意位置处压力和温度。
2 模型的求解
上述地层内的传热与传质模型与井筒内的传热与传质模型是通过产量公式耦合在一起,即


其中:PD为井指数,其表达式为[18]
g为单位时间单位体积储层中注入的蒸汽质量,kg/s;l为单位时间单位体积储层采出液量,kg/s;e为各向异性介质等价的各向同性渗透率,10−3µm2;p为变换的空间上网格内井段的长度,m;b为井格块等效半径,m;w为等效井径,m;为割缝筛管完井水平井表皮系数,采用FURUI[19]方法计算。
而对于地层内的传热与传质数学模型,由于稠油注蒸汽过程中地层内原油、地层水物性参数不仅受储层压力影响,还受温度的影响,故地层内传热与传质数学模型为强非线性模型。为保证所求模型的收敛性,本文采用全隐式方法对其进行求解。求解过程中,对于式(2)和式(3)中的蒸汽凝结项,求解时将式(2)和式(3)进行相加,将其抵消掉[20];然后联立蒸汽相热力学平衡式(5),就构成了由式(1)~(5)组成含4个未知数(g,w,,P)的方程组。考虑油、水的密度和焓均为温度和压力的函数,油和水的黏度为温度的函数,蒸汽的密度、黏度和焓均为温度的函数,对方程组进行全隐式差分后,即可通过块系数预处理共轭梯度法对其进行求解。
因此,地层与井筒内的传质与传热耦合模型可采用迭代方法对其求解,求解流程如下。
1) 对于蒸汽吞吐注入过程,定井底流压注入时可令水平井井筒压力、温度和干度均为水平井跟端压力、温度和干度,定产注入时则井筒压力可设为任意合理的井筒压力,井筒温度和干度均为水平井跟端温度和干度。
2) 利用块系数预处理共轭梯度法求解地层内传热与传质数学模型,即可得地层内压力、温度、饱和度及地层吸汽量。
3) 将所求得地层内压力、温度、饱和度及地层吸汽量带入井筒内传热与传质数学模型,便可得井筒内的压力、温度和干度。
4) 将最新的井筒内压力、温度和干度带入地层内传热与传质数学模型中重复计算,如此反复迭代,直到所求未知数满足一定的收敛条件,即得该时刻地层内压力、温度、饱和度、地层吸汽量及井筒内压力、温度和干度。
5) 重复过程1)~4),可求得蒸汽吞吐注入过程中任意时刻地层内压力、温度及井筒内压力、温度和干度。
6) 对于蒸汽吞吐生产阶段,定井底流压生产时可令水平井井筒压力均为水平井跟端压力,井筒温度为任意合理值,定产量生产时则井筒压力和温度均为任意合理的井筒压力和温度;重复议程1)~4),即可得蒸汽吞吐生产过程中任意时刻地层内压力、温度及井筒内压力、温度。
3 实例分析
以某区块实际地质与开发资料为依据,对所建模型进行验证,并对蒸汽吞吐水平井井筒入流规律进行研究。模型所需基本参数如下。
1) 油藏及流体参数:油藏埋深为1 047 m,油层厚度为10 m,孔隙度为0.354,渗透率为5 000×10−3μm2,原始地层压力为11.35 MPa,原始地层温度为53 ℃,含油饱和度为0.7,原油和水的密度分别为 955.977 kg/m3和1 006.89 kg/m3,原油和水的热膨胀系数分别为4.55×10−4℃−1和1.55×10−4℃−1,原油和水的压缩系数7.05×10−4MPa−1和5.25×10−4MPa−1,原油和水的比热容分别为2.2 kJ/(kg·℃)和4.2 kJ/(kg·℃),原油和水的焦耳汤姆逊系数分别为0.4 ℃/MPa和0.5 ℃/MPa,原油和水的黏度见表1,岩石密度为2 080.0 kg/m3,岩石比热容为1.24 kJ/(kg·℃),岩石压缩系数为7.686×10−3MPa−1,岩石导热系数为1.89 W/(m∙℃)。

表1 油和水的黏度
2) 水平井参数:水平井长度为200 m,割缝筛管内径为157.08 mm,外径为177.8 mm,井眼直径为194.46 mm,割缝长度为100 mm,割缝宽度为0.2 mm,割缝密度为280条/m,割缝筛管导热系数为48.85 W/(m.℃)。
3) 蒸汽吞吐注采参数:蒸汽温度为340 ℃,蒸汽干度为0.5,注入压力为14.78 MPa,生产阶段井底流压为9.78 MPa,注入时间为20 d,焖井时间为5 d,生产时间为125 d。
3.1 模型的可靠性验证
由于现有油藏数值模拟软件,如CMG和ECLIPSE,水平井井筒均假设为理想的裸眼完井,因此为验证所建模型的准确性,将本文所建模型预测理想裸眼完井水平井注汽量、日产油量和日产水量与CMG软件中灵活井模型(FW模型)预测结果进行对比,结果如图2所示。其中模型所划分网格数为31×25×1,网格长×宽×高为10 m×10 m×10 m。
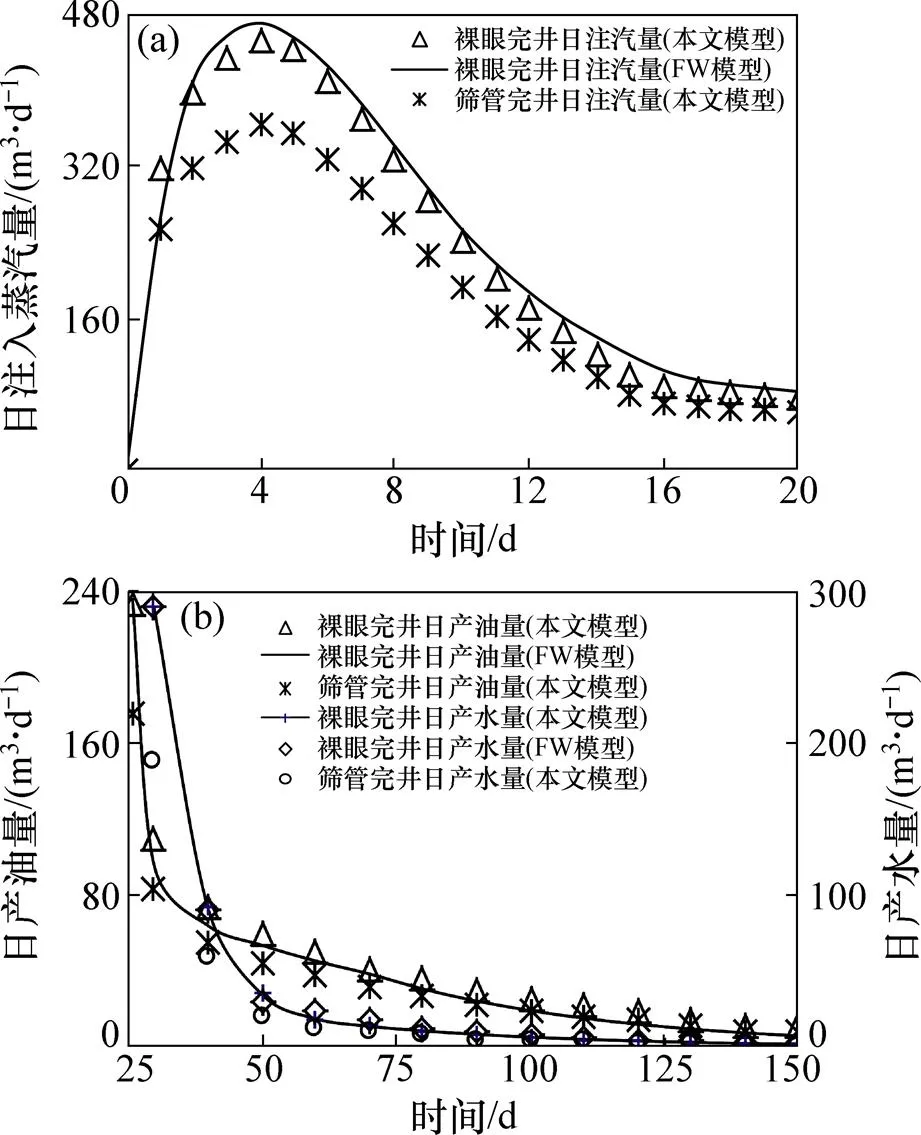
(a) 水平井日注汽量;(b) 水平井日产油量和产水量
由图2可知:本文模型计算的裸眼完井水平井日注汽量、日产油量和日产水量与灵活井模型计算结果相差不大,两者基本吻合,验证了模型的准确性。而由本文模型预测的割缝筛管完井水平井日注汽量、日产油量和日产水量均低于裸眼完井水平井,平均产能比分别为0.76,0.80和0.82。
由图2(a)可知:蒸汽注入初期,日注入蒸汽量较低,主要原因在于初始地层条件下,地层内原油和水黏度较高,流度较小,蒸汽很难进入地层,故日注入量较小;而随着蒸汽的不断注入,地层温度增加,油、水黏度均大幅度降低(表1),流体流度增加,蒸汽则能较容易地进入地层,故水平井日注蒸汽量增加;但当地层温度上升到一定程度,地层内原油和水的黏度降低幅度变小,此时随着注入时间的增加,地层压力升高,蒸汽日注入量下降。水平井定井底流压生产过程中,由于地层压力与温度不断下降,日产油量和日产水量均下降(见图2(b)和图2(c))。
3.2 注入过程中水平井井筒入流规律
蒸汽吞吐注入过程中水平井筒内压力、温度、蒸汽入流量及地层温度沿井筒分布如图3和图4所示。
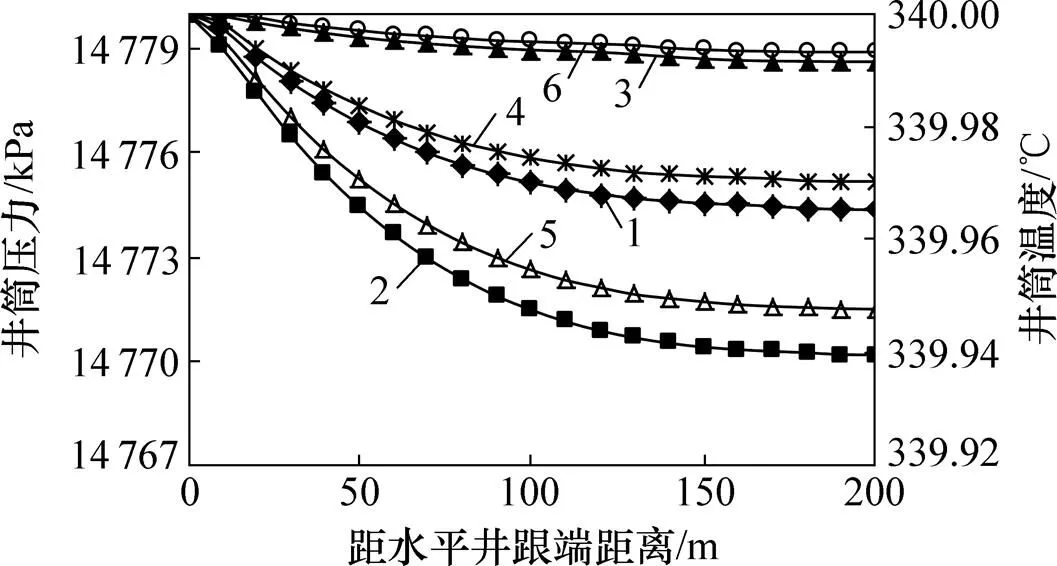
1—压力(1 d);2—压力(4 d);3—压力(12 d);4—温度(1 d);5—温度(4 d);6—温度(12 d)。

1—入流量(1 d);2—入流量(4 d);3—入流量(12 d);4—温度(1 d);5—温度(4 d);6—温度(12 d)。
由图3可知:由于井筒压降和热损失的存在,井筒压力与温度从水平井跟端到趾端均逐渐降低,且降低幅度越来越小;随着时间增加,水平井筒内蒸汽流量先增加后减小(图2(a)),因此,井筒压力和温度降低的幅度亦先增加后减小;但井筒压力和温度沿水平段变化幅度并不显著,最大只有10 kPa和0.052 ℃。
由图4可知:由于水平井跟端和趾端渗流面积较大,蒸汽在水平井跟端和趾端入流量高于水平井中部,入流剖面呈凹型分布;蒸汽的不均匀入流致使地层受热亦不均匀,地层温度沿井筒亦呈凹型分布;随着时间的增加,蒸汽入流剖面和地层温度沿井筒分布的非均质性亦增加,注入时间为1 d时,水平井跟端和趾端高入流量可达中部低入流量的1.10倍,而注入时间为4 d和12 d时,水平井跟端和趾端入流量分别可达中部低入流量的1.78和2.47倍,地层温度变化倍数则由1 d时的1.04倍升高到12 d时的1.28倍。
3.3 生产过程中水平井井筒入流规律
蒸汽吞吐生产过程中水平井筒内压力、温度、原油和地层水入流量如图5~8所示。

t/d:1—30;2—50;3—100;4—150。

t/d:1—30;2—50;3—100;4—150。

t/d:1—30;2—50;3—100;4—150。

t/d:1—30;2—50;3—100;4—150。
由图5可知:由于井筒内压降的存在,井筒压力从水平井趾端到跟端依次降低,但降低的幅度越来越大,且随着注入时间的增加,井筒内原油和水流量降低,产生的压降亦越低,故井筒压力呈下降的趋势。
由图6可知:由于井筒热损失,井筒内温度随着距水平井趾端距离的增加而逐渐降低,但在水平井跟端稍微升高,主要原因在于蒸汽注入阶段水平井跟端井筒温度和地层温度均较高所致;且温度沿水平井筒变化幅度较大,最大温度变化达30 ℃。
由图7和图8可知:由于水平井跟端和趾端渗流面积较大,原油和地层水在水平井跟端和趾端的入流量高于水平井中部,入流剖面呈凹型分布,且水平井跟端和趾端高入流量最高可达中部低入流量的1.24和1.12倍。
4 结论
1) 建立蒸汽吞吐割缝筛管水平井井筒与储层耦合数学模型,模型预测理想裸眼完井水平井日注汽量、日产油和日产水量与FW模型预测结果一致,预测该200 m割缝筛管完井水平井日注汽量、日产油和日产水量分别为理想裸眼完井水平井的0.76,0.80和 0.82倍。
2) 蒸汽吞吐注入过程中,井筒压力与温度从水平井跟端到趾端逐渐降低,但降低幅度并不显著;蒸汽入流剖面与地层温度沿井筒呈凹型分布,且随着时间的增加,蒸汽入流剖面与地层温度沿井筒的非均质性增加。
3) 蒸汽吞吐生产过程中,井筒压力从水平井趾端到跟端依次降低,而井筒温度却先降低后稍微增加;原油与地层水入流剖面沿井筒呈凹型分布。
[1] 陈绍云, 李瑷辉,李瑞营, 等. 大庆油田葡浅12区块浅层稠油水平井钻井技术[J]. 石油钻探技术, 2015, 43(1): 126−130. CHEN Shaoyun, LI Aihui, LI Ruiying, et al. Horizontal well drilling technology in shallow heavy oil recovery in block Puqian 12 of the Daqing oilfield[J]. Petroleum Drilling Techniques, 2015, 43(1): 126−130.
[2] 李晓益, 姚凯, 朱明. 哥伦比亚圣湖油田稠油油藏增产技术[J]. 石油钻探技术, 2015, 43(1): 100−105. LI Xiaoyi, YAO Kai, ZHU Ming. Stimulation technique for MECL heavy oil reservoirs in Colombia[J]. Petroleum Drilling Techniques, 2015, 43(1): 100−105.
[3] 王新东, 杨道平, 赵忠祥, 等. 哈萨克斯坦北布扎齐油田侧钻中短半径水平井完井工艺技术[J]. 石油钻探技术, 2006, 34(6): 30−32. WANG Xindong, YANG Daoping, ZHAO Zhongxiang, et al. Well completion techniques for medium-short radius horizontal wells sidetracked in north Buzachi, Kazakhstan[J]. Petroleum Drilling Techniques, 2006, 34(6): 30−32.
[4] 陈德民, 周金应, 李治平, 等. 稠油油藏水平井热采吸汽能力模型[J]. 西南石油大学学报, 2007, 29(4): 102−106. CHEN Demin, ZHOU Jinying, LI Zhiping, et al. A steam injection model for horizontal well in heavy oil reservoir with thermal recovery[J]. Journal of Southwest Petroleum University, 2007, 29(4): 102−106.
[5] 倪学锋, 程林松. 水平井蒸汽吞吐热采过程中水平段加热范围计算模型[J]. 石油勘探与开发, 2005, 32(5): 108−112. NI Xuefeng, CHENG Linsong. Calculating models for heating area of horizontal wellbore in steam stimulation[J]. Petroleum Exploration and Development, 2005, 32(5): 108−112.
[6] 刘春泽, 程林松, 刘洋, 等. 水平井蒸汽吞吐加热半径和地层参数计算模型[J]. 石油学报, 2008, 29(1): 101−105. LIU Chunze, CHENG Linsong, LIU Yang, et al. Calculating models for heating radius of cyclic steam stimulation and formation parameters in horizontal well after soaking[J]. Acta Petrolei Sinica, 2008, 29(1): 101−105.
[7] OBALLA V, COOMBE D A, BUCHANAN L. Aspects of discretized wellbore modeling coupled to compositional/thermal simulation[J]. Journal of Canadian Petroleum Technology, 1997, 36(4): 45−51.
[8] TAN T B, BUTTERWORTH E, YANG P. Application of a thermal simulator with fully coupled discretized wellbore simulation to SAGD[J]. Journal of Canadian Petroleum Technology, 2002, 41(1): 25−30.
[9] STONE T W, BENNETT J, HOLMES J A. Thermal simulation with multisegment wells[J]. SPE Reservoir Evaluation & Engineering, 2002, 5(3): 206−218.
[10] STONE T W, BENNETT J, EDWARDS D A, et al. A unified thermal wellbore model for flexible simulation of multiple tubing strings[C]//SPE Reservoir Simulation Symposium. Society of Petroleum Engineers. New York, 2011: 1291−1314.
[11] OBALLA V, BUCHANAN L. Flexible wellbore coupled to thermal reservoir simulator[C]//World Heavy Oil Congress. Puerto La Cruz, Venezuela, 2009: 1−8.
[12] CHEN H J, LI M Z, ZHANG Y Y, et al. Steam injection performance of horizontal wells completed with slotted liners[J]. Applied Mechanics and Materials, 2013, 423: 674−678.
[13] 吴永彬, 李秀峦, 孙新革, 等. 双水平井蒸汽辅助重力泄油注汽井筒关键参数预测模型[J]. 石油勘探与开发, 2012, 39(4): 481−488. WU Yongbin, LI Xiuluan, SUN Xinge, et al. Key parameters forecast model of injector wellbores during the dual-well SAGD process[J]. Petroleum Exploration and Development, 2012, 39(4): 481−488.
[14] LI Mingzhong, CHEN Huijuan, ZHANG Yanyu, et al. A coupled reservoir/wellbore model to simulate the steam injection performance of horizontal wells[J]. Energy Technology, 2015, 3(5): 535−542.
[15] 陈月明. 注蒸汽热力采油[M]. 东营: 石油大学出版社, 1996: 64−85. CHEN Yueming. Thermal recovery of steam injection[M]. Dongying: Press of University of Petroleum, 1996: 64−85.
[16] 王一平, 李明忠, 高晓, 等. 注蒸汽水平井井筒内参数计算新模型[J]. 西南石油大学学报(自然科学版), 2010, 32(4): 127−133. WANG Yiping, LI Mingzhong, GAO Xiao, et al. A new parameter-calculating model for steam flooding in horizontal wellbore[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(4): 127−133.
[17] 李明忠, 高晓, 巴燕, 等. 蒸汽吞吐水平井产液过程井筒传热与传质研究[J]. 石油钻采工艺, 2010, 32(3): 89−94. LI Mingzhong, GAO Xiao, BA Yan, et al. Research on wellbore heat and mass transfer of steamsoaking horizontal wellbore in oil production[J]. Oil Drilling & Production Technology, 2010, 32(3): 89−94.
[18] 李明忠, 陈会娟, 张贤松, 等. 煤层气多分支水平井井筒压力及入流量分布规律[J]. 中国石油大学学报(自然科学版), 2014, 38(1): 92−98. LI Mingzhong, CHEN Huijuan, ZHANG Xiansong, et al. Wellbore pressure and inflow rate distribution of multi-lateral horizontal well for coalbed methane[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014, 38(1): 92−98.
[19] FURUI K J. A comprehensive skin factor model for well completions based on finite element simulations[D]. Austin: University of Texas. Graduate School, 2004: 25−35.
[20] MOZAFFARI S, NIKOOKAR M, EHSANI M R, et al. Numerical modeling of steam injection in heavy oil reservoirs[J]. Fuel, 2013, 112: 185−192.
(编辑 赵俊)
Inflow performance of slotted horizontal wells in cyclic steam simulation process
CHEN Huijuan1, LI Mingzhong1, LIU Chunmiao2, LI Weiwei1, ZHANG Yanyu1
(1. College of Petroleum Engineering, China University of Petroleum, Qingdao 266580, China;2. Drilling & Production Technology Research Institute,CNOOC Energy Tech-Drilling & Production Co, Tianjin 300452, China)
Based on the string structure of the slotted horizontal wells, considering the variable mass flow of the fluid in horizontal wellbore, a coupled reservoir/wellbore model of horizontal wells for cyclic steam simulation was established. An iterative substitution method was used to solve the model. Based on the model, the inflow performance of the horizontal wells in steam injection period and fluid production period for cyclic steam simulation were studied. The results show that the wellbore pressure and temperature drop from the horizontal wellbore heel to toe in the steam injection period, but the decreased scope is insignificant. The steam influx rate and reservoir temperature profile along the horizontal wellbore is the concave shape and the non-uniformity of the steam influx rate and reservoir temperature along the wellbore increases with the increase of time. In the fluid production period, the wellbore pressure drops from the horizontal toe to the heel, but the wellbore temperature first decreases and then increases slightly. The oil and water influx rate profile along the horizontal wellbore are also the concave shape.
slotted liner; horizontal well; cyclic steam simulation; wellbore pressure; wellbore temperature; influx profile
10.11817/j.issn.1672-7207.2016.06.030
TE319
A
1672−7207(2016)06−2037−08
2015−06−29;
2015−09−23
国家科技重大专项(2011ZX05024-005);中央高校基本科研业务费专项资金资助项目(14CX06025A)(Project (2011ZX05024-005) supported by the National Science and Technology Major Program of China; Project(14CX06025A) supported by the Fundamental Research Funds for the Central Universities)
陈会娟,博士,从事油气田开发方面的研究;E-mail:iichj@126.com

