贯通型单台阶岩体结构面剪切性质及应用
黄达,黄润秋,雷鹏
贯通型单台阶岩体结构面剪切性质及应用
黄达1, 2,黄润秋3,雷鹏1
(1. 重庆大学土木工程学院,重庆,400045;2. 重庆大学煤矿灾害动力学与控制国家重点实验室,重庆,400044;3. 成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川成都,610059)
利用二维颗粒流(PFC2D)方法模拟研究台阶高长比(/)对贯通型单台阶岩体结构面剪切变形及强度影响。研究结果表明:台阶损伤破坏模式可分为压切和张剪破坏2种基本类型,随着/增大,压切模式逐渐转化为张剪模式,但其与法向应力基本无关。当台阶张剪损伤破坏时(>0.45),受弯矩及剪切力偶合作用,台阶根部易张裂;当台阶压切损伤破坏时(≤0.45),主要受斜向上的剪切力作用而使其尖角剪断,沿剪切面呈现明显的爬坡效应,具剪胀特性。针对实际岩体结构面台阶高长比/常较小(压切模式),建立同时考虑结构面爬坡与啃断效应的剪切强度经验公式,并运用于边坡稳定性计算的参数取值。
岩体力学;结构面;剪切变形;剪切强度;颗粒流
岩体结构面地质力学性质对岩体稳定性及加固设计均有非常重要的影响。岩体结构面力学性质与壁岩特性(壁岩成分、强度、结构构造等)、结构面结合状态(充填度、充填物成分、充填胶结强度)和结构面起伏形态有关[1−6]。尤其是无充填型结构面表面起伏形态对其剪切变形、损伤破坏及强度等性质影响显著[5−6]。结构面粗糙起伏一般可分为平直结构面、锯齿状结构面、波状起伏结构面、台阶状结构面这4种基本类 型[6]。目前主要集中于诸如规则锯齿状及波状起伏型结构面的破损及强度等力学效应研究。研究发现,当法向应力相对较低时,结构面在剪切时沿突齿斜面滑移爬坡,出现剪胀现象;而当法向应力超过某一临界值时,倾斜粗糙面上的滑动被抑制,将剪切啃断锯 齿[7]。HOMAND等[8]基于低法向应力(小于5 MPa)、小截面尺寸(长150 mm×宽150 mm)和较小齿状起伏的花岗岩结构面循环直剪试验,分析了剪切前后锯齿结构面表面面积的衰减变形规律,定量描述了低法向应力循环剪切条件下锯齿状结构面磨损随法向应力增强的特性。周辉等[9]研究了水泥砂浆锯齿状结构面在不同起伏高度、不同剪切速率和不同法向压力条件下声发射参数的变化规律和发生机制。李海波等[10−12]采用混凝土试件开展了锯齿型结构面剪切强度及变形等力学特性直剪试验研究。目前,针对具凸起台阶状结构面的剪切性质方面的研究相对较少。郭志[13]采用石膏试件开展了台阶高为1.0,0.5,1.0和1.5 cm且高长比 (/)为0.06,0.16,0.30和0.50台阶状结构面的直剪试验,发现峰值强度与残余强度之差随着高长比/的增大而增大。但试验试件太小,尺寸效应明显,且由于试验设备等限制而没有揭示结构面损伤破裂演化。利用颗粒流程序(particle flow code,PFC)开展岩石力学试验其主要优点在于避免了设定材料宏观本构的经验主观行为,而是通过颗粒接触黏结机理从细观尺度仿真岩石矿物颗粒及其间的黏结与摩擦来实现宏观材料的组构,反映了颗粒胶结型岩石类材料的本质细观结构属性[14]。POTYONDY等[15−17]采用PFC模拟了多种岩石宏细观力学特性,较充分地阐述或论证了PFC模拟在研究岩石裂隙扩展、细观损伤演化及力学性质等方面的科学优势。为了丰富对台阶状结构面剪切特性的研究,本文作者首先从理论上探讨台阶状结构面剪切特性,进而利用颗粒流程序开展较大长度且具有不同高长比(/)单台阶岩体结构面试件直剪数值试验。从颗粒细观位移、裂纹演化及剪切应力−位移曲线等方面研究台阶状结构面剪切变形的细宏观多尺度演化过程;建立综合考虑结构面基本摩擦角、岩石黏聚力b及台阶高长比/的台阶状结构面剪切强度经验公式。
1 结构面凸起台阶压剪破裂理论 分析
具有台阶状起伏形态的外倾结构面在斜坡(坡体常为层状或块裂结构)的浅表生改造带常见,特别是在反倾层状岩质斜坡的浅表层,顺层斜坡也偶有出现。斜/边坡稳定状态明显受外倾贯通型结构面的凸起岩石台阶所控制性,即受岩石台阶规模及强度等综合控制。根据一般的固体力学理论,可得到2点单台阶结构面剪切性质的定性认知:1) 当台阶高远大于台阶长时,台阶如同悬臂梁一样,台阶根部既有剪力作用又有弯矩作用,在这种复合应力的作用下,台阶根部岩石更易于张剪复合破坏甚至弯曲折断;2) 当台阶高远小于台阶长时,台阶岩石主要受剪切力作用而弯矩很小,结构面易剪断台阶尖角滑移。在绝大多数情况下,在凸起台阶前方(剪切方向)岩体结构面的延伸长度要比凸起台阶的高度大得多,故真实岩体的台阶型结构面常满足远小于。
若台阶长度足够长且假设剪裂面通过台阶脚点,则建立如图1所示的结构面凸起台阶剪切破裂模型。图1中:虚斜线为假设的剪切破裂面;为台阶高;为台阶长;n和分别为结构面上法向应力和剪切应力;′n和′分别为作用在斜面上的正应力和切应力;为台阶剪切破裂面倾角。破裂面上正应力′n和剪应力′分别为:
图1 凸起岩石台阶剪切破裂模型
Fig. 1 Shear fracture model for a raised rock step
由库仑准则可知台阶剪裂面上抗剪应力′r为
式中:b和分别为完整岩石的黏聚力和摩擦角。
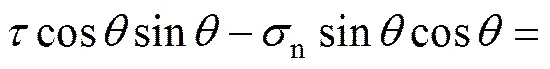
(4)
此时,台阶的剪切应力为
式(5)对求导,则式(5)在极值条件下可求得斜面倾角=45°−b/2,再代入式(5),得台阶的临界剪切应力为
由于凸起台阶最不利剪切破裂面与水平面的夹角=45°−b/2,而此时台阶高和长需满足<tan(45°−b/2)。
2 台阶状结构面直剪试验PFC模拟
2.1 数值模型及参数标定
图2所示为台阶状结构面PFC2D数值模型,其中,正方形模型边长为0.4 m,贯通闭合型单台阶岩体结构面两侧颗粒用深色示意。定义6道墙作为边界条件(侧墙5,6和2,3均以结构面为分界点),对构建下部剪切盒的边界墙(如图2中1,2和6墙)进行法向变形约束,对上部剪切盒两侧墙(如图2中3和5墙)赋予一定的同向等量移动速度(剪切速率)即可对试样施加水平剪切推力(图2中箭头表示墙运动方向),恒定的法向荷载可通过编制伺服系统程序不断地调整上部墙(如图2中4墙)的位移速度实现。
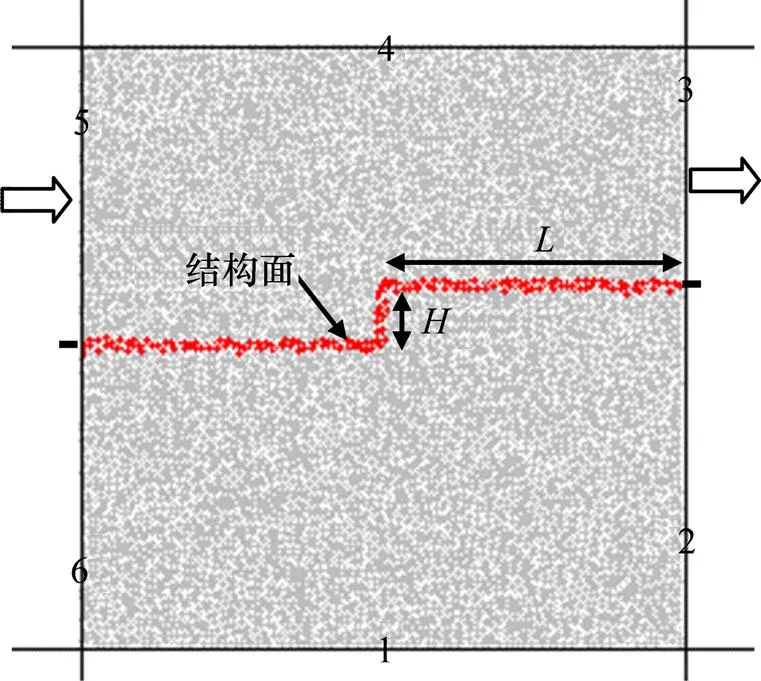
图2 台阶状结构面PFC2D数值模型
模型台阶长均设定为0.2 m,台阶高长比/设定为0.10,0.20,0.30,0.40,0.45,0.50和0.60,法向荷载n设为3.5,5.0,6.5,8.0和12.0 MPa,剪切速率为0.005 mm/s。选用较符合岩石细观颗粒间组构的平行黏结接触模型(parallel-bonded model),其不但可模拟岩石细观颗粒间的法向和切向受力方式,而且可模拟颗粒间因胶结形成的力矩[15]。
通过单轴压缩、直剪数值试验测试岩体宏观参数与室内试验结果相匹配来实现细观参数的标定。较简单有效的标定步骤为:1) 将平行黏结法向强度b,m和切向强度b,m设为较大的值,通过改变颗粒接触模量c和平行黏结模量来匹配岩石宏观弹性模量;2) 改变颗粒刚度比n/s和平行黏结刚度比来匹配岩石泊松比;3) 改变b,m和b,m来匹配单轴压缩强度;4) 改变颗粒摩擦因数等细观参数来匹配岩石内摩擦角和黏聚力。选用重庆地区常发育台阶状裂隙的三叠系下统嘉陵江组白云岩作为原型,经过颗粒间细观逼近宏观力学参数的目标调试,最终确定一组较可靠的平行黏结模型细观参数,如表1所示。表2所示为PFC数值试验宏观参数与室内试验结果的比较,图3所示为在5 MPa法向应力作用下白云岩直剪试验与PFC直剪模拟剪应力−剪切位移曲线图。由表2和图3可知:表1中的岩石的细观参数较真实地反映了试验白云岩的细观组构及力学性质。平直近光滑的贯通型白云岩结构面的基本摩擦角r为35.5°。
表1 PFC模型细观参数
Table 1 Meso-mechanical parameters of PFC model

表2 室内试验测得试样宏观参数与PFC模拟结果比较
Table 2 Comparison of macro properties for the specimens tested in lab and by PFC simulation
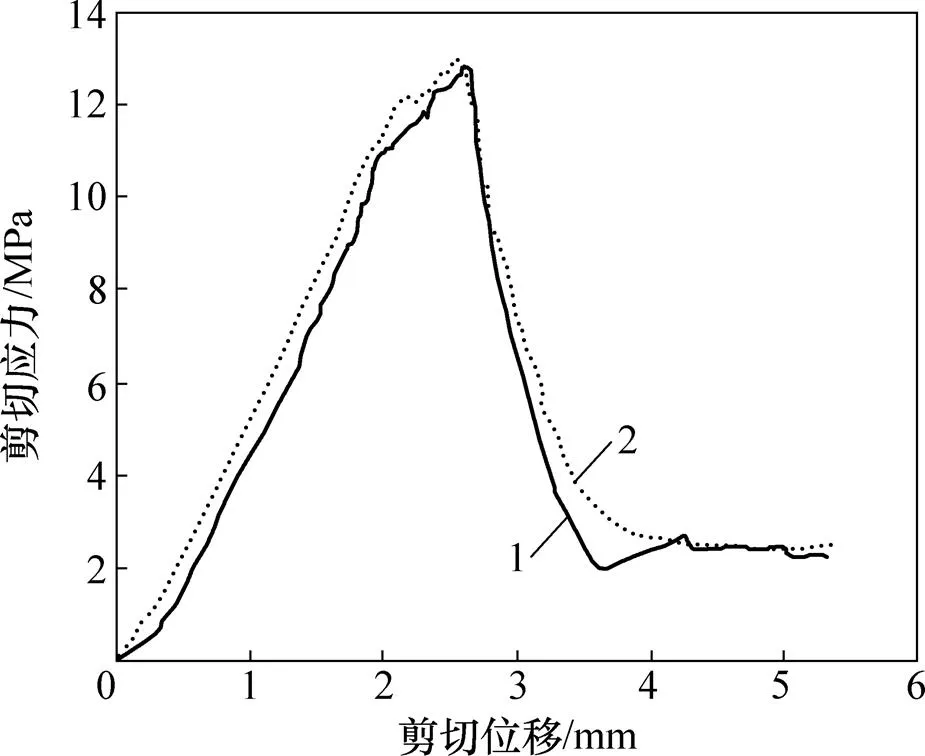
1—直剪试验;2—PFC模拟。
2.2 台阶损伤破坏模式及演化
作为一种离散元方法,颗粒流程序能从细宏观多尺度模拟结构面的剪切变形和破坏。基于裂纹发展、分布及位移矢量的分析表明,直立台阶的损伤破坏模式主要受其高长比的影响,而法向应力的影响相对很少。按台阶高长比的不同,变形破坏模式可分为2类:当台阶高长比>0.45时,凸起台阶将张剪破坏;当台阶高长比≤0.45时,凸起台阶将压切破坏。与第2节理论分析凸起台阶沿最不利剪切破裂面压切破坏时需满足<tan(45°−b/2)=0.479基本吻合,显示了颗粒流方法的可靠性。
2.2.1 张剪损伤破坏
图4所示为结构面台阶高长比=0.5、法向应力n=5 MPa时剪切过程中剪应力及累积微裂纹数随剪切变形的演化曲线。根据剪应力−位移及微裂纹−位移曲线,将剪切过程分为3个阶段:弹性阶段(图4中点之前),峰前累进损伤阶段(图4中段),峰后破坏阶段(图4中点之后)。峰前累积损伤段剪应力−位移曲线呈小幅多频性波动,微裂纹稳步增加;在峰值点后应力跌落幅度较大,跌落过程中微裂纹数显著增加。

(a) 剪应力−位移曲线;(b) 微裂纹−位移曲线▲—剪切状态1;●—剪切状态2;■—剪切状态3
图5所示为图4中3个不同剪切状态时刻结构面凸起台阶裂纹扩展及位移矢量。台阶上角点(上尖角)类似于点荷载顶压及剪切推力的综合作用下,致使上角点左上方(后上方)岩体首先出现张剪复合裂纹(图5(a))。由于台阶高长比相对较大,随着剪切力的增加,凸起台阶处的位移矢量表明台阶既受弯矩作用又受剪力作用,故台阶根部易于在弯矩作用下张裂而形成张拉裂纹(图5(b)~(c))。两角点附近的宏观张性裂纹倾伏向下且倾伏角小于25°(图5(c)),随高长比减小而逐渐减小,当=0.45时几乎为0°(近水平)。

(a) 剪切状态1;(b) 剪切状态2;(c) 剪切状态3
2.2.2 压切损伤破坏
图6所示为结构面台阶高长比=0.4、法向应力n=5 MPa时剪切过程中剪应力及累积微裂纹数随剪切变形的演化曲线。相对于图4中的张剪模式,压切模式存在2点明显区别:峰后应力跌落幅度(即峰值与残余应力差)相对较小;累进损伤及峰后破坏过程中产生相对更多的微裂纹。

(a) 剪应力−位移曲线;(b) 微裂纹−位移曲线
图7所示为图6中3个不同剪切状态时刻结构面凸起台阶裂纹扩展及位移矢量。凸起台阶处的位移矢量表明台阶主要受斜向上的剪切力作用,这就是水平剪切推力作用下使相对较小的台阶尖角剪断的变形响应(沿如图7(c)所示的剪裂面剪断),致使台阶根部及上尖角附近应力集中,台阶根部及上尖角附近岩体相继压剪损伤,造成此两处微裂纹发育且宏观上呈压碎状(如图7(b))。压切破坏模式沿剪切面呈现明显的爬坡效应,结构面出现张裂架空(见图7(c)),具剪胀性质。
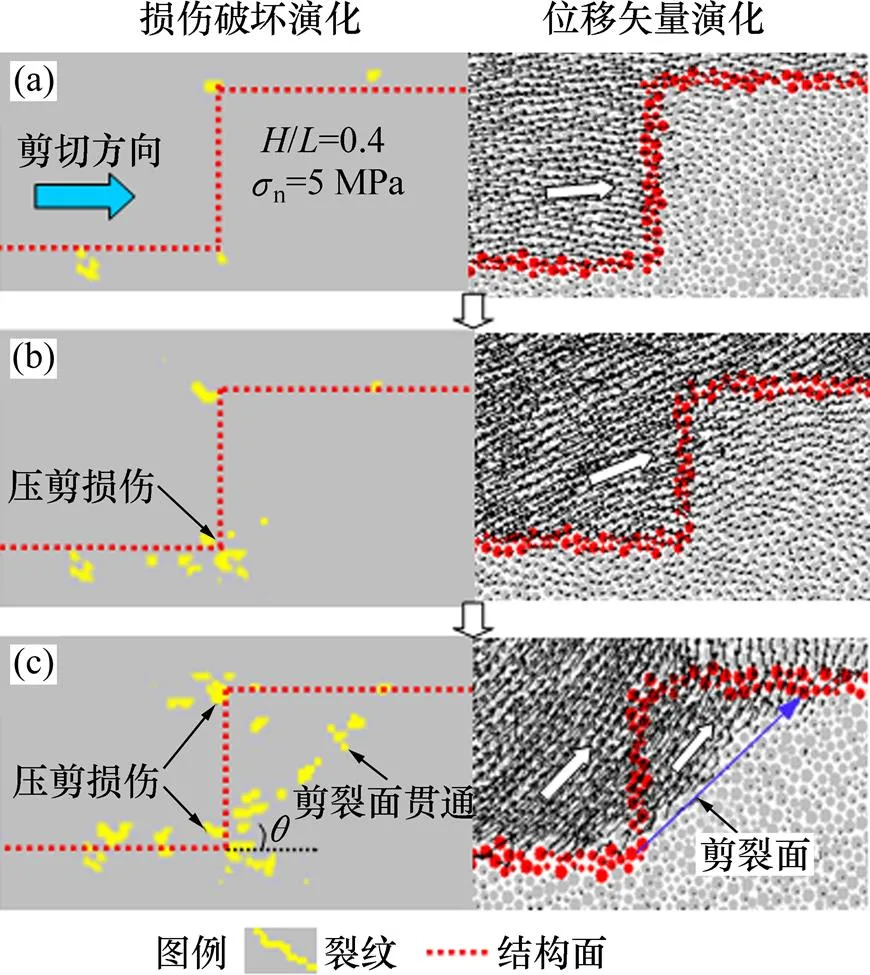
(a) 剪切状态1;(b) 剪切状态2;(c) 剪切状态3
3 结构面剪切强度
结构面抗剪强度一般通过Mhor−Coulomb屈服准则确定。由前述的讨论可知,当台阶高长比> 0.45时,台阶是在弯矩和剪力联合作用下张剪破坏,显然这时利用Mhor−Coulomb准则不恰当。而实际结构面台阶的高长比均比较小,故这里只探讨当<0.45的情况。
为了使台阶状岩体结构面强度公式的物理意义更明确,构建其剪切强度公式为
4 边坡稳定性算例
假设顺向贯通型单台阶结构面控制的某白云岩边坡如图9所示,坡高为16 m,坡角为65°,离坡顶左侧10 m。固定结构面点的位置不变,调整点位置,设置台阶高长比/分别为0.1,0.2,0.3和0.4。结构面基本摩擦角为35.5°,岩石黏聚力b为 9.05 MPa,摩擦角为38.8°,其他参数见表2。下面采用极限平衡法(平面滑移)和强度折减法分别计算这4种/工况时边坡的稳定性。

图9 单台阶结构面边坡模型
4.1 极限平衡计算
台阶状潜在滑动面和图6所示的微裂纹分布图表明台阶状滑动带主要沿台阶起伏区域损伤贯通。故假设如图9所示台阶起伏的虚线区域为滑动带,且台阶起伏的中线视为宏观滑动面。按照图9计算模型,则稳定性系数,即
式中:R为抗滑力;为宏观滑裂面的倾角;为滑体的质量。
台阶状结构面抗剪强度采用经验式(8)确定,则抗滑力R可表示为
4.2 强度折减法计算
强度折减法的基本原理是将岩体抗剪强度参数黏聚力和摩擦角同时乘以一折减系数s,得到一组新的′和′,然后作为新的材料参数进行计算,当边坡失稳时,对应的s称为边坡的安全系数。
采用FLAC−2D进行强度折减法安全系数计算,计算模型与图9所示的一致。台阶状结构面采用接触面单元interface模拟。边坡左边界、右边界及下边界均采用法向位移约束。利用剪应变增量、塑性区范围及连通状态和迭代求解的不收敛性综合判定临界稳定状态。同时对结构面及图9中虚线区域内潜在滑动带岩体的抗剪强度参数按相同的折减系数s折减,从而求得边坡安全系数。
图10和图11所示分别为单台阶(高长比=0.1)结构面边坡临界滑动时塑性区与剪切应变增量分布图。此时塑性区基本贯通,剪切滑动带基本形成,且大致沿图9中所假设的损伤带滑动。台阶屈服且其顶部尖角剪应变增量明显集中。
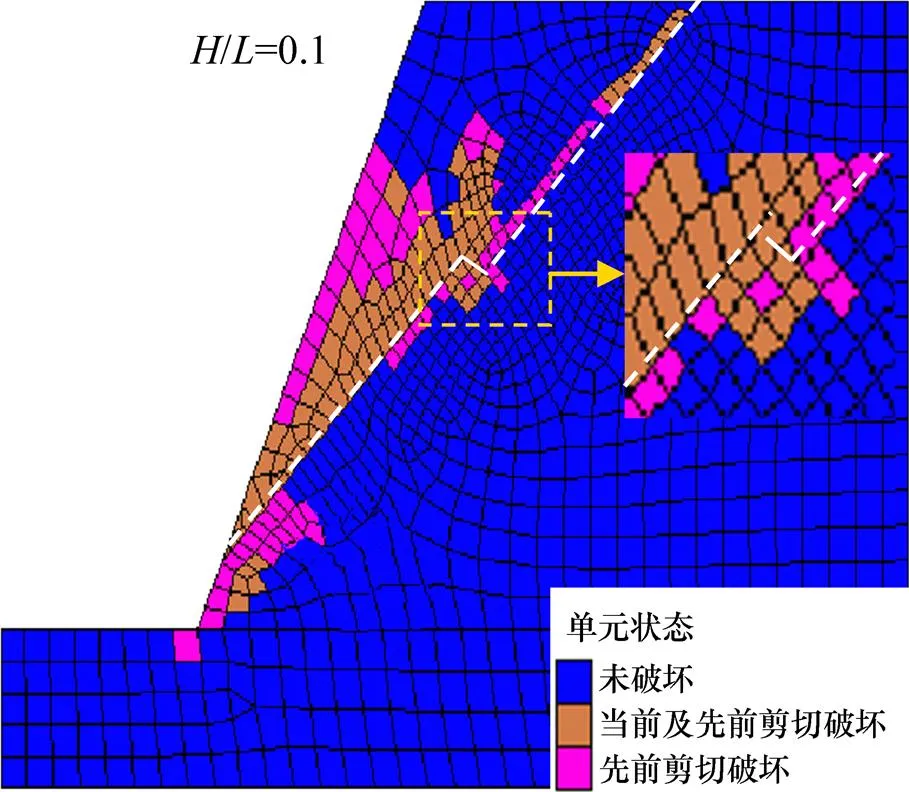
图10 边坡塑性区
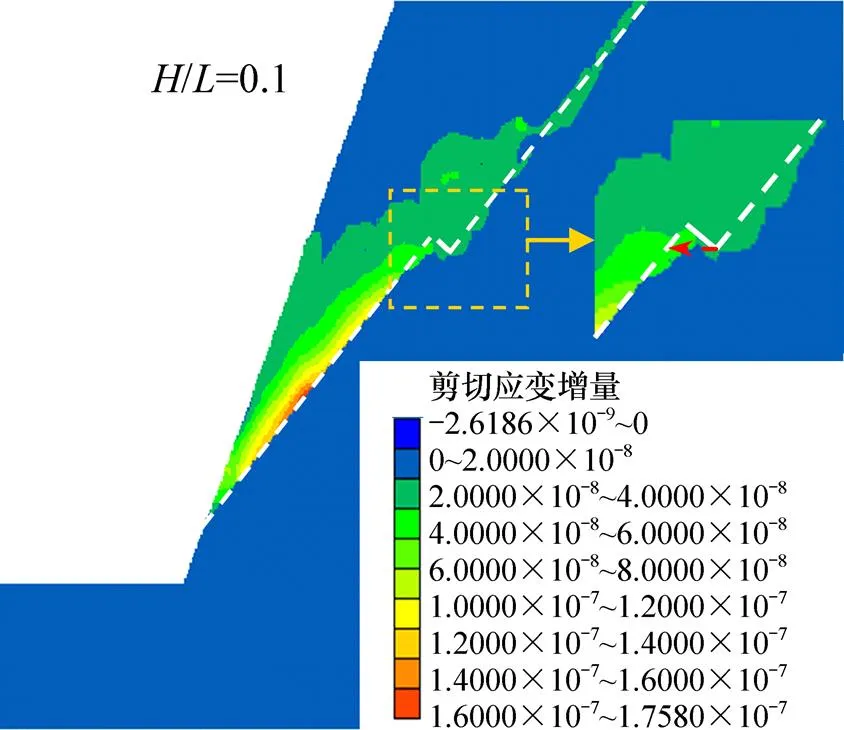
图11 边坡剪切应变增量
4.3 2种方法比较分析
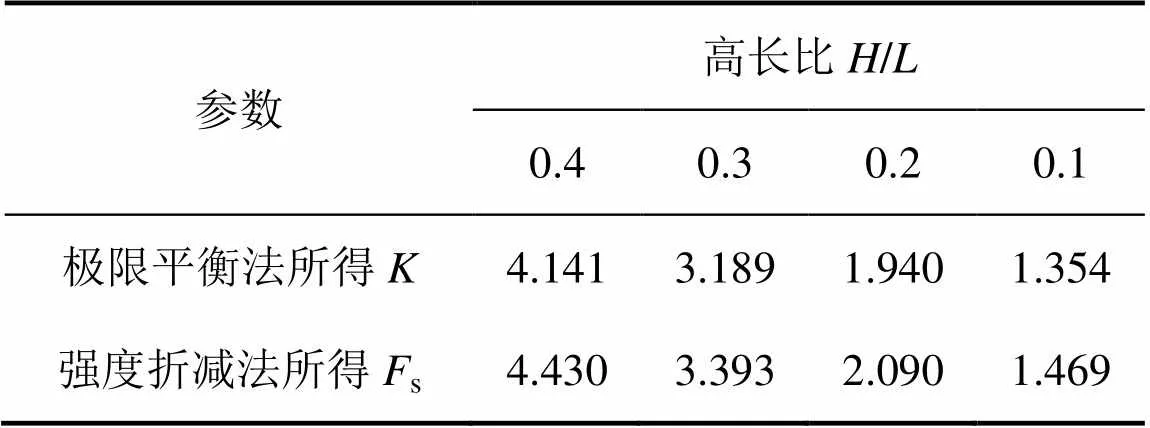
表3所示为2种方法稳定性计算结果。虽然极限平衡计算的稳定性系数与强度折减法计算的安全系数s存在一定的差别(这与其基本概念的定义不同相关),其中强度折减法计算结果相对偏大。但这2种方法计算结果随台阶高长比的变化规律基本一致,也可表明本文建立的强度估算式(7)及式(8)基本合理,同时也反映了颗粒流程序计算剪切强度的可靠性。
表3 极限平衡法和强度折减法稳定性计算结果
Table 3 Results of stability calculation using limit equilibrium methods and strength reduction methods
5 结论
1)岩体结构面台阶可分为压切损伤破坏(台阶高长比≤0.45)和张剪损伤破坏(>0.45)模式。随着增大,弯矩作用逐渐增强,由压切逐渐转化为张剪模式。但其损伤破坏模式与法向应力基本无关。
2) 对于张剪损伤破坏模式,凸起台阶既受弯矩作用又受剪力作用,台阶根部易于在弯矩作用下张裂而形成张拉裂纹。台阶两角点附近的宏观张性裂纹倾伏向下且倾伏角随减小而减小,当=0.45时几乎为0°。
3) 对于压切损伤破坏模式,台阶主要受斜向上的剪切力作用而使其尖角剪断,沿剪切面呈现明显的爬坡效应,具剪胀性质。
4) 实际岩体结构面台阶高长比常较小,针对压切损伤破坏模式,建立了同时考虑结构面爬坡效应和啃断效应的剪切强度经验公式,通过边坡稳定性算例分析,验证了此公式的合理性。
[1] 刘博, 李海波, 刘亚群. 循环剪切荷载作用下岩石节理变形特性试验研究[J]. 岩土力学, 2013, 34(9): 2475−2481. LIU Bo, LI Haibo, LIU Yaqun. Experimental study of deformation behavior of rock joints under cyclic shear loading[J]. Rock and Soil Mechanics, 2013, 34(9): 2475−2481.
[2] 王姣, 李长冬, 雍睿, 等. 三峡库区侏罗系不同类型结构面抗剪强度对比[J]. 煤田地质与勘探, 2014, 42(5): 61−66. WANG Jiao, LI Changdong, YONG Rui, et al. Comparison study on shear strength parameters of Jurassic different rock discontinuities in Three Gorges Reservoir region[J]. Coal Geology & Exploration, 2014, 42(5): 61−66.
[3] INDRARATNA B, JAYANATHAN M, BROWN T. Shear strength model for overconsolidated clay-infilled idealised rock joints[J]. Géotechnique, 2008, 58(1): 55−65.
[4] 孙辅庭, 佘成学, 万利台. 充填水泥浆岩石节理峰值剪切强度模型[J]. 岩石力学与工程学报, 2014, 33(12): 2481−2489. SUN Futing, SHE Chengxue, WAN Litai. A peak shear strength model for cement filled rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(12): 2481−2489.
[5] BARTON N. Shear strength criteria for rock,rock joints,rockfill and rock masses: problems and some solutions[J]. Journal of Rock Mechanics & Geotechnical Engineering, 2013, 5(4): 249−261.
[6] 周瑞光. 岩体结构面形态的力学效应[J].工程勘察, 1981, 9(1): 46−51. ZHOU Ruiguang. Mechanics effect of discontinuity surface morphology in rock mass[J]. Geotechnical Investigation & Surveying, 1981, 9(1): 46−51.
[7] EINSTEIN H H, VENEZIANO D, BAECHER G B, et al. The effect of discontinuity persistence of rock slope stability[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1983, 20(5): 227−236.
[8] HOMAND F, BELEM T, SOULEY M. Friction and degradation of rock structural plane surfaces under shear loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(10): 973−999.
[9] 周辉, 孟凡震, 张传庆, 等. 结构面剪切过程中声发射特性的试验研究[J]. 岩石力学与工程学报, 2015, 34(S1): 2827−2836. ZHOU Hui, MENG Fanzhen, ZHANG Chuanqing, et al. Experimental study of acoustic emission characteristic of discontinuity under shearing condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 2827−2836.
[10] 李海波, 刘博, 冯海鹏, 等. 模拟岩石结构面试样剪切变形特征和破坏机制研究[J]. 岩土力学, 2008, 29(7): 1741−1746. LI Haibo, LIU Bo, FENG Haipeng, et al. Study of deformability behavior and failure mechanism by simulating rock joints sample under different loading conditions[J]. Rock and Soil Mechanics, 2008, 29(7): 1741−1746.
[11] 沈明荣, 张清照. 规则齿型结构面剪切特性的模型试验研究[J]. 岩石力学与工程学报, 2010, 29(4): 713−719. SHEN Mingrong, ZHANG Qingzhao. Experimental study of shear deformation characteristics of rock mass discontinuities with regular surface roughness[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 713−719.
[12] 张清照, 沈明荣, 丁其文. 结构面在剪切状态下的力学特性研究[J]. 水文地质工程地质, 2012, 39(2): 37−41. ZHANG Qingzhao, SHEN Mingrong, DING Qiwen. Study on the mechanical properties of rock mass discontinuity under shear condition[J]. Hydrogeology and Engineering Geology, 2012, 39(2): 37−41.
[13] 郭志. 实用岩体力学[M]. 北京: 地震出版社, 1996: 30−68. GUO Zhi. Practical rock mass mechanics[M]. Beijing: Seismological Press, 1996: 30−68.
[14] Itasca Consulting Group Inc. Manual of particle flow code in 2-dimension: theory and background[M]. 3.1st ed. Minneapolis: Itasca Consulting Group Inc, 2004: 1−4.
[15] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329−1364.
[16] POTYONDY D O. The bonded-particle model as a tool for rock mechanics research and application: current trends and future directions[J]. Geosystem Engineering, 2014, 17(6): 342−369.
[17] BEWICK R P, KAISER P K, BAWDEN W F. Shear rupture under constant normal stiffness boundary conditions[J]. Tectonophysics, 2014, 634(11): 76−90.
(编辑 刘锦伟)
Shear properties of through-going discontinuity with a rock step and its application
HUANG Da1, 2, HUANG Runqiu3, LEI Peng1
(1. School of Civil Engineering, Chongqing University, Chongqing 400045, China;2. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China;3. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology, Chengdu 610059, China)
The influence of the ratio () of height () to length () of a rock step on shear deformation and strength for through-going discontinuity was investigated by 2D particle flow code (PFC2D) simulation method. The results show that the damage-failure modes of rock step can be concluded into two basic types: compression-shear failure and tension-shear failure. With the increase of the/of the rock step, the damage-failure mode gradually evolves from compression-shear to tension-shear failure. And the damage-failure modes do not pertain to the normal stress. For the tension-shear failure mode (>0.45), the tensile crack is easily formed by rifting in the root of the rock step as the raised step is subjected to bending moment and shear force. For the compression-shear failure mode (≤0.45), the shear dilatation characteristics can be shown mainly due to the action of the up-sloping shear force which can cause that the sharp corners of the rock step sheared off and generate climbing effect along shear surface. For the/of a rock step in the actual slopes is often small relatively, and an empirical shear strength equation is established in which both the
rock mass mechanics; discontinuity; shear deformation; shear strength; particle flow code (PFC) effects of climbing along shear surface and the rock step gnawed are considered. The empirical equation can be applied to the estimation of shear strength parameter of the discontinuity with a rock step to calculate the slope stability.
10.11817/j.issn.1672-7207.2016.06.027
TD313
A
1672−7207(2016)06−2015−08
2015−06−25;
2015−08−09
国家自然科学基金资助项目(41472245,41130745);重庆市国土房管科技计划项目(CQGT-KJ-2014049);中央高校基本科研业务费重大项目(106112016CDJZR208804)(Projects(41172243, 41130745) supported by the National Natural Science Foundation of China; Project(CQGT-KJ-2014049) supported by the Chongqing Administration of Land, Resources and Housing; Project (106112016CDJZR208804) supported by the Fundamental Research Funds for the Central Universities)
黄达,博士,教授,博士生导师,从事岩土工程和工程地质研究;E-mail:dahuang@cqu.edu.cn

