瞬变电磁快速三维正演

李瑞雪，王鹤, 2，席振铢, 2，蒋欢，刘愿愿



瞬变电磁快速三维正演

李瑞雪1，王鹤1, 2，席振铢1, 2，蒋欢1，刘愿愿1

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 中南大学海洋矿产探测技术与装备研究所，湖南长沙，410083)

为了提高瞬变电磁法三维正演计算速度，一方面，采用矢量有限单元法与积分方程法相混合，使24维单元矩阵的阶数降低到12维，减少大型稀疏矩阵的计算时间，同时增强边界条件的连续性，避免出现伪解；另一方面，引进Flow-through Hankel transform快速计算技术，解决不同收发距的贝塞尔函数重复计算的问题，进一步节省计算时间。研究结果表明：引入矢量有限单元法的混合法和Flow-through Hankel transform快速计算技术不但能保证3维计算精度，而且能提高计算速度。

瞬变电磁法；3维正演；Flow-through Hankel transform；矢量有限单元法

瞬变电磁法以其灵敏度高、探测深度大、分辨率高以及适应性强的优点，已经迅速发展为地球物理勘探方法中常用方法，但其正、反演技术进展缓慢，特别是3维计算速度不能满足实际工程应用的要求[1−2]。瞬变电磁3维正演方法主要有有限差分法、有限单元法和积分方程法[3−4]。其中，有限单元法和有限差分法计算速度慢，占用内存大[5−7]；积分方程法只适合模拟简单模型[8−9]。BAKR等[10]使用迭代混合解法求解扩散电磁场，该方法先设定1个边界场的初始值，求出内部场，然后根据傅里叶变换求出新的边界场，一直重复这个过程，直到计算结果误差在规定范围内为止。这种算法适用于异常体与围岩的电导率差很小的模型，但当电导率差达200倍时，这种算法精度不高。CHUNG等[11]提出了1种基于求解二次磁场的正演方法，克服了基于总场求解只适合于电导率差小的模型的缺点。GUPTA等[12−13]将节点有限元法和积分方程法结合进行瞬变电磁3维正演，在保证计算精度的基础上成倍提高了计算速度，但会导致伪解，并引起边界条件不连续。在瞬变电磁的数值模拟中，麦克斯韦方程推导的电磁场的表达式是含0阶或者1阶贝塞尔函数的积分形式，因为贝塞尔函数不收敛，求解这类积分必须用到汉克尔变换。国内外学者针对这方面进行了大量研究。GUPTASARMA等[14]求解了0阶汉克尔变换的61点和120点滤波系数、1阶汉克尔变换的47点和140点滤波系数，提高了计算速度和精度。但瞬变电磁法二次场的计算将异常体作为场源，导致收发距在每个测点都不同，因此，需要重复进行汉克尔变换求解贝塞尔函数，耗费大量的计算时间。RAICHE[15]使收发距与汉克尔滤波系数同步对数等间隔变化，避免了重复计算贝塞尔函数。为此，本文作者一方面将矢量有限单元法和积分方程法结合实现瞬变电磁3维正演中大型矩阵的降维快速计算，另一方面运用Flow-through汉克尔变换快速计算技术，解决不同收发距贝塞尔函数重复计算的问题，进一步节约计算时间。为了表达方便，将该方法称为改进混合 算法。

1 理论基础

1.1 降维快速计算原理

在各向同性的3维均匀介质中，忽略位移电流和磁流密度，电磁场满足麦克斯韦方程[13]：

其中：()，()，，和()分别为电场强度、磁场强度、磁导率、电导率和电流密度。

对式(1)求散度，并将式(2)代入，同时将电场分解为一次电场和二次电场，可得二次电场的扩散方程：

其中：()，()和分别为二次电场、一次电场和电导率异常。

对异常体和边界围岩区域进行网格剖分，剖分网格为线性等参六面体，在每个单元内二次电场的近似解为[16]

则单元内的余量为

引入伽辽金法，令单元内余量加权为0，得

将式(6)代入式(7)，考虑单元内全部12个形函数，则在每个单元内式(7)可写为

其中：为12×12阶单元矩阵；为12×1阶列向量；为与源有关的矩阵。

对所有单元方程式(8)进行组合得方程组：

其中：为稀疏矩阵；1为与源有关的向量。将二次电场()分为异常体内部二次电场和边界二次电场，则式(9)变为

其中：为对权矢量和场矢量采用内部棱边形函数得到的刚度矩阵；为对权矢量采用内部棱边形函数、对场矢量采用边界棱边形函数得到的刚度矩阵。和有类似的含义。

将式(10)写为总场的形式，并引入积分方程法[13]，可得

其中：G1和G2分别为一次电场和二次电场的格林函数。式(11)方程组阶数通常是几百阶，可采取直接解法求解，求得一次电场强度。最后，根据

可求出二次磁场强度。其中：()为层状介质中的一次磁场强度；G2为二次磁场的格林函数。

1.2 Flow-through快速汉克尔变换

考虑含贝塞尔函数的积分：

其中：J0()为0阶第一类贝塞尔函数；为源点和接收点的距离，且

式中：为采样起始点；为采样间隔；=1， 2，…，。

由式(14)可见：()只与收发距有关。但瞬变电磁法中二次场的计算将异常体看作发射源，因此，每个测点的收发距都不同，常规的快速汉克尔变换在每个收发距下都得进行1次，浪费了大量重复计算时间。Flow-through 汉克尔变换[15]提供了1种新的计算思路。令汉克尔变换的系数和收发距都呈对数等间隔分布，式(13)将变为

其中：为常数；为对数等间隔分布的收发距；w为汉克尔滤波系数；x为汉克尔滤波系数横坐标值。

从式(15)可以看出汉克尔变换的计算时间主要受2个方面的影响：1) 汉克尔系数的节点数；2) 函数值的计算次数。其中，第2个方面的影响远大于第1个方面的影响，因此，可以通过对函数值的重复利用来减少计算时间。故令收发距对数等间隔分布，在每个数量级取15个点进行计算。令最小的收发距1比实际测量中的最小收发距小，最大的收发距k比实际测量中的最大收发距大。因为x也是对数等间隔分布的，定义

则式(15)变为

对1个固定的收发距k来说，定义它所需的最小汉克尔系数为n，它所需的最大汉克尔系数为n。显而易见，计算最小收发距1时需计算最大汉克尔系数n，计算最大收发距k时需计算最小汉克尔系数n，故在实际程序中需用n到n的汉克尔系数。因此，

为了满足所有收发距范围，令收发距从10−1m到104m呈对数等间隔分布。在计算过程中，首先对于最小收发距1，求取对应滤波系数n1到n的函数值并存储，同时计算此时的积分值。其次，对于最大收发距k，求滤波系数n到n1对应的函数值并存储，同时求取积分值。在计算其他收发距时，直接调用已经储存的函数值，节约计算时间。

程序伪代码如下：

!n是1和2的中间值

=1

DO=0，2

n=

计算并存储

计算(1)

IF (|Re()|<|Re()|*10−6or |Im()|<|Im()|*10−6)

EXIT

END DO

DO=0−1,1, −1

n1=

计算并存储

计算(1)

IF (|Re()|<|Re()|*10−6or |Im()|<|Im()|*10−6)

EXIT

END DO

=

DO=n1−1,1, −1

n=

计算并存储

计算(k)

IF (|Re()|<|Re()|*10−6or |Im()|<|Im()|*10−6)

EXIT

END DO

！求取积分

DO=2，−1

DO=n，n

计算(k)

END DO

END DO

对于实际的任意收发距，判断出它在k和k+1之间，通过3次样条插值算出对应的函数值。这种计算方法避免了不同收发距下的函数值的重复计算，提高了计算效率，节约了计算时间和内存。

2 数值计算精度与速度比对

2.1 数值计算精度比对

检验数值计算精度的最好途径是与解析解比对。瞬变电磁法均匀半空间具有解析解，不失一般性，选择电阻率为100 Ω∙m均匀大地进行比对。

对于电阻率为100 Ω∙m的均匀半空间，划分出长×宽×高为100 m×100 m×100 m的区域进行均匀网格剖分，分别是方向(−50 m，50 m)，方向(−50 m，50 m)，方向(−50 m，−150 m)。这3个方向各有5个节点，在地面布1条测线，从(−200 m，0 m)到(200 m，0 m)，共11个测点。发射线圈采用100 m×100 m的方形回线，电流为1 A。计算机为ThinkPadE430，i5-3210M处理器，4G内存，计算时间为390 s(11个测点，每个测点125个网格)。计算结果见图1，具体误差见表1。

从图1可见：程序模拟的均匀半空间曲线和解析解得出的曲线形态基本一致，也基本重合。由表1可见：除早期的几个点外，电流归一化感应电动势相对误差基本在10%以内，满足精度要求，可以用来计算更复杂的地电模型。

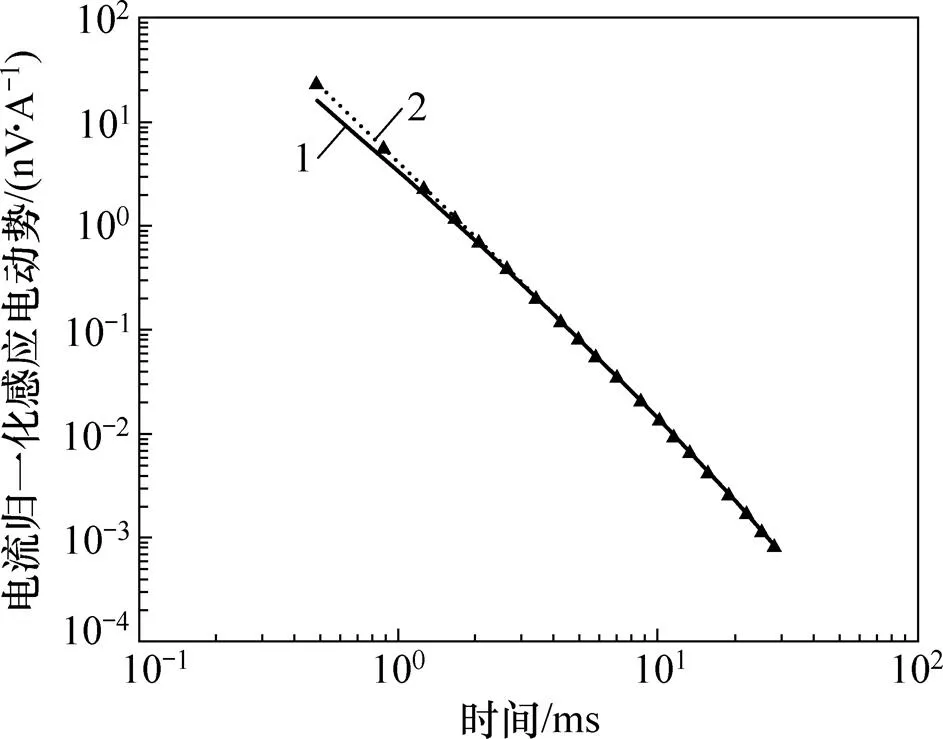
1—改进混合算法解；2—解析算法解。

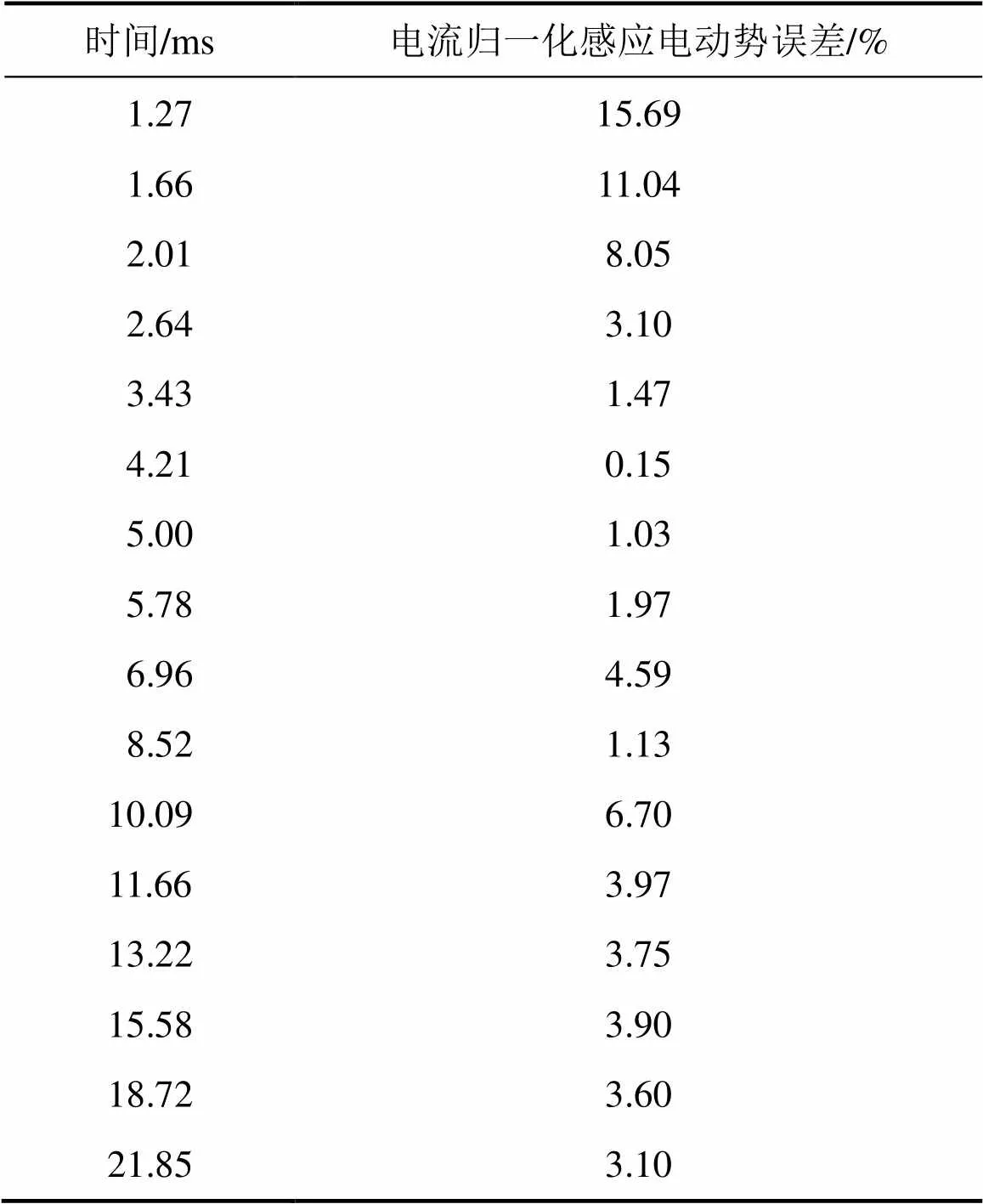
表1 不同时刻下改进混合算法误差

2.2 数值计算速度比对

为了验证改进混合算法计算速度，通过模拟直立薄板模型响应与2.5维有限单元法、3维积分方程法进行比对。

直立薄板模型如图2 所示。在电阻率为100 Ω∙m的均匀半空间下有电阻率为1 Ω∙m的异常体，异常体走向为方向，范围为(−200 m，200 m)，沿方向范围为(−15 m，15 m)，方向范围为(50 m，200 m)，可以认为是直立薄板。在地面布测线1条，从(−300 m，0 m)到(300 m，0 m)，共25个测点，发射线圈采用100 m×100 m的方形回线，电流为1 A。假设接收线圈为1个点，响应结果和计算时间见图3。

由图3可见，该算法与2.5维有限单元法和积分方程法得到的曲线形态基本一致，在异常体区域曲线完全重合。混合算法的计算时间是2.5维有限单元法的10%，与积分方程法相比，计算速度提高了28%，体现了该算法的快速性。

图2 直立薄板模型

1—改进混合算法，20 min；2—2.5维有限元法，3.0 h；3—3维积分方程法，28 min。

3 3维快速计算算例

电阻率为100 Ω∙m的均匀半空间中地表下方有1个长方体，其电阻率为1 Ω∙m，走向为方向，具体范围为(−200 m，200 m)；方向范围为(−100 m，100 m)，方向范围为(50 m，250 m)。发射线圈采用100 m×100 m的方形回线，电流为10 A，接收线圈为1个点。布置7条测线，测线沿方向，7条测线的坐标在(−300 m，300 m)内均匀分布；每条测线13个测点，在(−300 m，300 m)内均匀分布，具体模型如图4所示。为了保证计算精度，对上述异常体进行均匀网格剖分，共剖分为8×5×5个单元，网格剖分如图5所示。

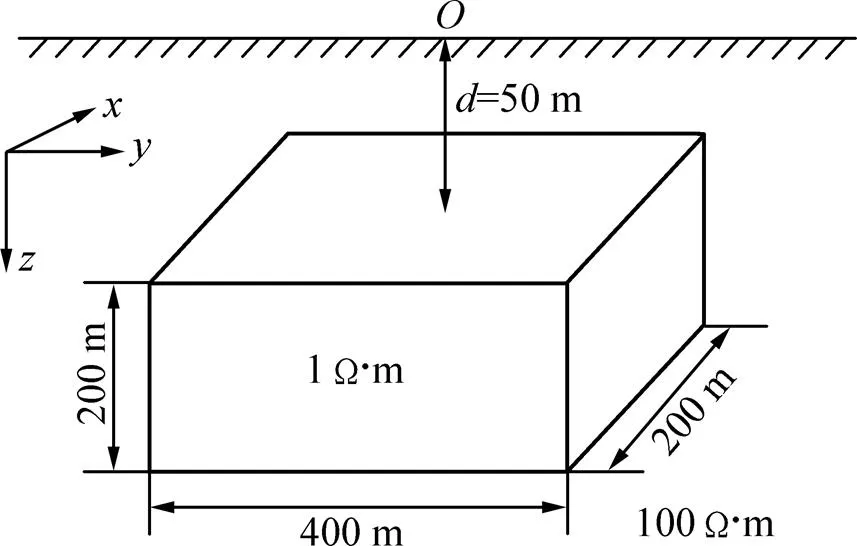
图4 3维长方体模型示意图

图5 3维长方体网格剖分示意图

计算所用电脑为ThinkPadE430，i5-3210M处理器，4G内存，计算时间为3 430 s，平均1条测线(13个测点，每个测点324个单元)运算时间为490 s，计算结果如图6所示。因为异常体埋深较浅，因此，在=0.5 ms时，长方体的响应已经十分明显，随着时间的延长，二次场逐步衰减，探测深度逐渐加深，异常体响应越来越弱，直到=25 ms时异常响应完全消失。由图6可知：程序正演结果所得异常与物理模型中异常基本对应，异常范围与物理模型异常范围也基本符合，进一步验证了程序的正确性和快速性，也说明了3维正演的必要性。

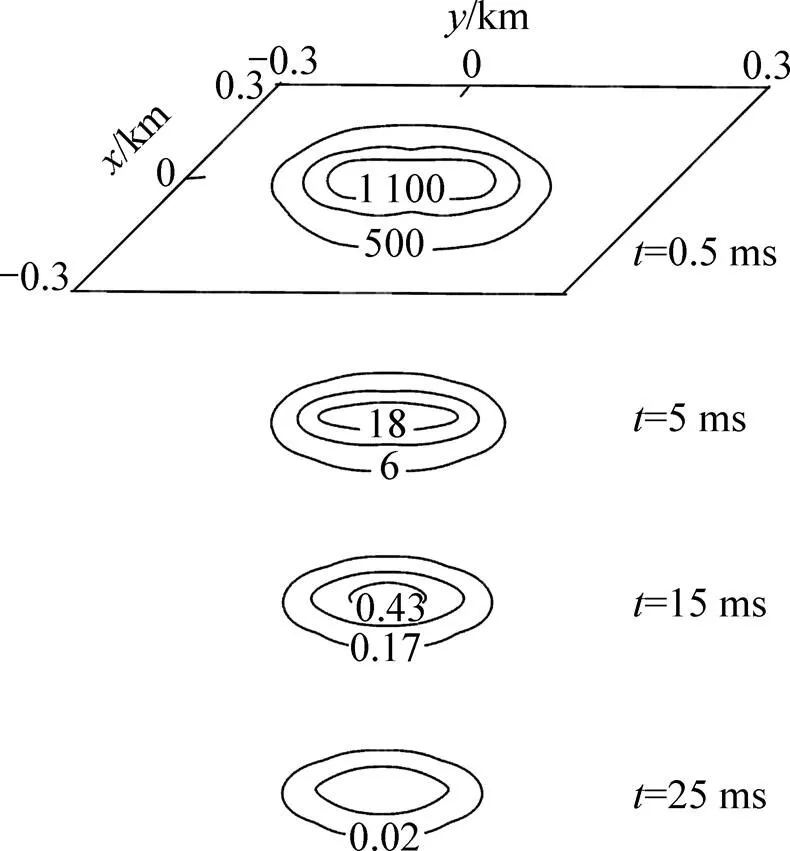
图中数值单位：nT/s

4 结论

1) 将矢量有限单元法和积分方程法相混合，降低了单元矩阵的阶数，减少了大型稀疏矩阵的计算时间，增强了边界条件的连续性，提高了3维计算精度。

2) 引进Flow-through Hankel transform快速计算技术，解决了不同收发距的贝塞尔函数重复计算浪费时间的问题，提高了计算速度。

3) 改进混合算法不但能够保证3维计算精度，而且提高了计算速度，促进了瞬变电磁3维正演技术的发展。

参考文献：

[1] 牛之链. 时间域电磁法原理[M]. 长沙: 中南大学出版社, 2007: 1−6. NIU Zhilian. Theory of time domain electromagnetic method[M]. Changsha: Central South University Press, 2007: 1−6.

[2] 李貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 2002: 1−4. LI Xiu. The theory and application of transient electromagnetic sounding[M]. Xi’an: Shanxi Science and Technology Press, 2002: 1−4.

[3] 薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 2008, 23(4): 1165−1172. XUE Guoqiang, LI Xiu, DI Qingyun. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics, 2008, 23(4): 1165−1172.

[4] 李建慧, 朱自强, 曾思红, 等. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 2012, 27(4): 1393−1400. LI Jianhui, ZHU Ziqiang, ZENG Sihong, et al. Progress of forward computation in transient electromagnetic method[J]. Progress in Geophysics, 2012, 27(4): 1393−1400.

[5] EPOV M I, SHURINA E P, NECHAEV O V. 3D forward modeling of vector field for induction logging problems[J]. Russian Geology and Geophysics, 2007, 48(9): 770−774.

[6] 李建慧. 基于矢量有限单元法的大回线源瞬变电磁法三维数值模拟[D]. 长沙: 中南大学地球科学与信息物理学院, 2011: 3−7. LI Jianhui. 3D numerical simulation for transient electromagnetic field excited by large source loop based on vector finite element method[D]. Changsha: Central South University School of Geosciences and Info-Physics, 2011: 3−7.

[7] 孙怀凤, 李貅, 李术才, 等. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J]. 地球物理学报, 2013, 56(3): 1049−1064.SUN Huaifeng, LI Xiu, LI Shucai, et alThree-dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese Journal of Geophysics, 2013, 56(3): 1049−1064.

[8] SWIDINSKY A, EDWARDS R N. The transient electromagnetic response of a resistive sheet straight forward but not trivial[J]. Geophysics Journal International, 2009, 179(3): 1488−1498.

[9] 张辉, 李桐林, 董瑞霞. 体积分方程法模拟电偶源三维电磁响应[J]. 地球物理学进展, 2006, 21(2): 386−390. ZHANG Hui, LI Tonglin, DONG Ruixia. Modeling 3-D electromagnetic responses of the electric dipole using volume integral equation method[J]. Progress in Geophysics, 2006, 21(2): 386−390.

[10] BAKR S A, MANNSETH T. An approximate hybrid method for electromagnetic scattering from an underground target[J]. Geoscience and Remote Sensing, IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 99−107.

[11] CHUNG Y, SON J S, LEE T J, et al. Three-dimensional modelling of controlled-source electromagnetic surveys using an edge finite-element method with a direct solver[J]. Geophysical Prospecting, 2014, 62(6): 1468−1483.

[12] GUPTA P K, BENNETT L A, RAICHE A P. Hybrid calculations of the three-dimensional electromagnetic response of buried conductors[J]. Geophysics, 1987, 52(3): 301−306.

[13] GUPTA P K, RAICHE A P, SUGENG F. Three-dimensional time-domain electromagnetic modelling using a compact finite-element frequency-stepping method[J]. Geophysical Journal International, 1989, 96(3): 457−468.

[14] GUPTASARMA D, SINGH B. New digital linear filters for Hankel J0and J1transforms[J]. Geophysical Prospecting, 1997, 45(5): 745−762.

[15] RAICHE A. A flow-through Hankel transform technique for rapid, accurate Green’s function computation[J]. Radio Science, 1999, 34(2): 549−555.

[16] 金建铭. 电磁场有限元法[M]. 西安: 西安电子科技大学出版社, 1998: 176−182. JIN Jianming. The finite element method in electromagnetics[M]. Xi’an: Xi Dian University Press, 1998: 176−182.

(编辑 陈灿华)

Fast 3D forward modeling of transient electromagnetic

LI Ruixue1, WANG He1, 2, XI Zhenzhu1, 2, JIANG Huan1, LIU Yuanyuan1

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;2. Marine Mineral Exploration Technology and Equipment Institute, Central South University, Changsha 410083, China)

In order to enhance the speed of 3D transient electromagnetic forward modeling, two new techniques were employed. One is combining vector finite-element method with integral equation method to decrease the order of elemental matrix from 24 to 12, which can save much time of the computing large sparse matrix, keep the continuity of boundary conditions, and avoid spurious solutions; the other is adopting flow-through Hankel transform technique to resolve the exhausted time problem through calculating. Bessel function repeatedly while resetting the offsets every time. The results show that the two new techniques not only keep the accuracy of 3D TEM forward technique but also speed up the calculation.

transient electromagnetic method; 3D forward modeling; Flow-through Hankel transform; vector finite-element method

10.11817/j.issn.1672-7207.2016.10.026

P319.1+2

A

1672−7207(2016)10−3477−06

2015−10−12；

2015−12−24

大洋“十二五”重大项目(DY125-11-R-03)；国家自然科学基金资助项目(41304090)；深圳市战略新兴产业发展专项资金资助项目(CXZZ20120618165608947)(Project(DY125-11-R-03) supported by the Ocean Major during “Twelfth Five Year Plan”; Project(41304090) supported by the National Natural Science Foundation of China; Project(CXZZ20120618165608947) supported by Strategic Emerging Industry Development Special Foundation of Shenzhen)

席振铢，教授，博士生导师，从事瞬变电磁方法与技术研究；E-mail：xizhenzhu@163.com