求解一类双层规划的自适应变异动态差分进化算法

吴亮红，徐睿，左词立，曾照福，段伟涛



求解一类双层规划的自适应变异动态差分进化算法

吴亮红，徐睿，左词立，曾照福，段伟涛

(湖南科技大学信息与电气工程学院，湖南湘潭，411201)

针对一类上层函数和约束函数不具有凸性和可微性要求，而下层函数可微且凸的非线性双层规划问题，首先通过Karush−Kuhn−Tucher(KKT)条件将双层规划问题转换为单层约束非线性规划问题，并结合非固定多段映射罚函数法和精确罚函数法对约束条件进行无约束化处理，然后提出一种改进的动态差分进化算法优化对系列无约束优化问题进行求解。对8个测试实例进行数值计算并与现有算法进行比较。测试结果表明，所提方法是一种求解该类双层规划问题的有效方法。

双层规划；KKT条件；罚函数法；差分进化算法

双层规划问题(BLPP)是一类具有主从递阶结构的系统优化问题。由于这种模型更能描述实际系统的阶层关系和更全面地体现决策者的意愿，故在经济、军事、交通、电力和工程等众多领域具有十分重要的理论意义和应用背景[1−2]。一般来说，求解双层规划非常困难，这主要包括2方面的原因。一方面，双层规划问题是1个NP-hard问题，HANSEN等[3]证明即使是最简单的双层线性规划也是强NP-Hard问题。VICENTE等[4]指出甚至寻找双层线性规划问题的局部最优解也是1个NP-Hard问题。另一方面，由于上层优化问题的目标函数取决于下层优化问题的解函数，而这个解函数一般是非线性且不可微的，故双层优化问题是1个非凸优化问题。双层优化问题本质的非凸性以及非处处可微性给其数值求解带来极大困难，因此，对于非线性双层规划问题，设计有效求解算法仍是当前的研究热点。在过去的20 多年中，人们对双层规划问题进行了许多研究，并取得了一些理论、数值和应用研究成果，总体来说可分为以下3种类型。1) 基于数值计算的精确算法。这类算法大多是针对一些具有良好问题特性的双层规划问题，如求解线性和二次双层规划的分枝定界法[3]等。其通用方法是利用KKT(Karush−Kuhn−Tucker)条件代替下层规划问题，将双层规划问题转化为1个约束单层规划问题，然后用数值计算方法进行求解。2) 精确方法与启发式算法的结合。其做法通常是利用KKT条件将双层规划问题转化为单层规划问题，然后用启发式算法求解该单层规划问题，如求解线性双层规划的GA算法[5]和混合禁忌搜索算法[6]、求解非线性双层规划的进化算法[7]等。3) 层次启发式算法。该类算法是一种求解双层规划问题的一般算法，对上、下层目标函数和约束没有任何特殊要求，上、下层优化算法均采用启发式算法，通常采取嵌套方式集成在一起，如求解双层规划问题的PSO算法[8]、层次遗传算法[9]、差分进化算法[10]等。然而，这类算法由于采取嵌套方式，对于每个上层个体都必须调用1次下层启发式算法求得相应的下层最优解，其计算代价很大。另一方面，若下层启发式算法陷入局部最优解，则得不到相应的上层全局最优解。本文着重研究第2种类型的求解方法。差分进化(differential evolution, DE)算法是由STORN 和 PRICE 共同提出的一种启发式优化算法[11]。DE算法原理简单，受控参数少，易于理解和实现，实施随机、并行、直接的全局搜索，是当前最有效的进化算法之一[12]。然而，由于原创DE算法在每一代进化过程中种群始终保持不变，直到被下一代种群所替代，因此，从种群更新角度，DE算法本质上是一种静态结构，它没有立即跟踪当前种群的进展状况，存在一代时延。显然，静态种群更新方式会导致算法收敛速度变慢。针对以上不足，QIN等[13]采用动态更新种群方式对DE/best/1/bin进化机制进行改进，提出一种动态差分进化策略(dynamic differential evolution,DDE)。DDE利用最新更新的种群生成试验矢量，从而加快算法的收敛速率[14]。本文针对一类上层函数和约束函数不具有凸性和可微性要求而下层函数可微且凸的非线性双层规划问题，通过KKT条件[15−16]将双层规划问题转换为单层非线性约束优化问题，分别应用非固定多段映射罚函数法对不等式约束以及精确罚函数法对等式约束进行无约束化处理，然后应用动态差分进化算法对等价系列无约束优化问题进行求解。为进一步提高算法的收敛性能，结合DDE的2种不同变异机制优点，采用自适应策略平衡算法的全局搜索和局部开发能力，提出一种改进的DDE算法，对8个Benchmarks测试实例进行数值实验。

1 双层规划问题

双层规划问题最初用于描述市场经济中的寡头行为。在双层规划模型中，上、下层决策者控制相应的决策变量，并优化各自的目标函数。其中，下层优化问题的最优化解决了上层优化问题的可行解空间。下层决策者首先进行决策，这样上层决策者必须考虑下层的可能反应。下层决策者根据上层的决策进行响应，以优化自身目标函数。因为双方可供选择的策略集是相互依赖的，上层的决策会影响下层可选的决策和目标实现，反之亦然。

设上层决策矢量为=(1，…，x)∈R，下层决策矢量为=(1，…，y)∈R，BLPP的数学模型定义如下：

其中：(,)和(,)分别为双层规划的上层目标函数和约束函数，而(,)和(,)分别为下层目标函数和约束函数。若所有函数均为线性函数，则该问题为线性双层规划，否则为非线性双层规划(NBLP)。本文主要研究一类(,)和(,)没有凸性和可微性等特殊要求而(,)和(,)是可微且凸的NBLP问题。

2 问题转化

由于本文研究的是一类下层问题可微且凸的双层规划，设上层和下层约束条件个数分别为和，则对于每个固定的上层决策矢量，下层优化问题可等价于1个KKT驻点问题：

其中：E(,,)为式(2)中的前2项等式，即(,)和(,)的非线性不等式部分；h(,,)为它们的非线性等式部分；+y−为(,)和(,)的所有线性部分。

尽管KKT条件将该类双层规划问题转化为单层规划问题，但相应的约束条件有所增加且维数增多。式(3)中不等式主要由目标函数给出，并且包含拉格朗日算子皆为非负数的条件；等式约束来源于式(2)，为的维数。对于该约束优化问题，由于约束条件较多且上层优化问题非凸不可微，一般算法难以求解，因此，本文采用混合罚函数法对约束进行处理，其中不等式约束采用非固定罚函数法而等式约束采用精确罚函数法。同时，为了求得该问题的全局最优解，本文提出一种具有良好收敛性能的自适应动态差分进化算法对该问题进行求解。

3 混合罚函数法

一般地，在处理式(3)这类优化问题时，罚函数法是比较常见的无约束处理方法之一。其基本思路是在目标函数中加上1个能反映满足约束的惩罚项，从而构成1个无约束的广义目标函数；再利用优化算法对这个无约束优化问题进行计算寻优，利用惩罚项的作用，使得算法找到问题的最优解。

在通常情况下，构造的广义目标函数形式为

()=()+()() (4)

其中：()为原目标函数；()()为惩罚项，()为惩罚力度，()为惩罚因子。若式(4)中的()固定不变，则称该罚函数法为精确罚函数法或固定罚函数法，否则为非固定罚函数法。非固定罚函数法可以克服固定罚函数法中()难以选取的问题，该值若过大，则会在可行域边界造成目标函数产生病态，导致计算困难。反之，若该值过小，则会导致收敛减慢甚至不收敛。在非固定罚函数法中，()随迭代次数的变化而动态调节，可避免()的选取问题。

由于问题(3)包含若干个等式约束，且约束条件较复杂，在直接使用非固定多段映射罚函数法对问题(3)进行无约束处理的过程中，该方法虽然能保证问题(3)在不等式约束存在的情况下进行有效寻优，但是对于若干个等式约束的处理存在较大偏差。若将等式直接改写成2个相应的不等式，即h()=0等价为h()≤0且h()≥0，会导致因约束过强而算法难以收敛。鉴于以上实际问题，采用精确罚函数法与非固定罚函数法相结合的策略。其中，对于不等式约束部分，采用非固定多段映射罚函数法，而对于等式约束部分，采用精确罚函数法，这样既可有效将问题(3)无约束化，又可简化惩罚力度的选取，使得问题得到有效解决。修正后的混合罚函数法为

其中：(,)为上层目标函数；为迭代次数；()为所有不等式约束函数；()为所有等式约束函数；为精确罚函数的惩罚力度；1为非固定多段映射罚函数的惩罚因子；2为精确罚函数的惩罚因子。式(7)表示不等式约束条件对约束的违背程度，式(8)表示其对应的罚函数的强度，式(9)为多段映射函数，式(10)为随变化的惩罚力度。通过以上约束处理方式，可将式(3)约束优化问题转化为无约束优化问题。

4 自适应动态差分进化算法

动态差分进化(DDE)算法的进化算子与原创DE完全相同，两者的最大区别在于个体的动态更新方式不同[14]。对于DDE算法，若1个新生成的试验矢量比其目标矢量具有更优的适应度，则试验矢量替代目标矢量且立即更新当前种群参与其后的进化操作。与原创DE算法相比，DDE算法由于总是利用最新更新的种群生成试验矢量，且无需额外的存储空间来保存下一代父代种群，因此，具有更快的收敛速率。然而，对于DE/best/1/bin策略，动态更新种群虽然加快了收敛速率，但更容易使算法陷入局部最优点。因此，为了平衡算法的全局搜索和局部开发能力，本文结合DE/rand/1/bin全局搜索能力强和DE/best/1/bin局部开发能力强的优势，提出一种具有良好收敛性能和鲁棒性的自适应变异机制动态差分进化算法(SADDE)，求解式(5)所示的优化问题。

4.1 自适应变异操作

在进化的每一代，DDE算法通过变异操作为当前种群中的每个个体()=(x1,x2, …,x)生成1个目标个体() =(v1,v2, …,v)(其中，为当前迭代次数)。目前，DE算法已发展多种不同方式的变异机制。其中，基于“rand”变异方式的DDE算法能很好地保持种群多样性，从而有较强的全局搜索能力，但也存在收敛速率较慢的问题；而基于“best”变异方式的DDE算法以当前种群中适应度最高的个体作引导，具有较强局部开发能力和较大收敛速率，但很容易陷入局部收敛。综合考虑这2种变异机制的特点，本文提出一种自适应变异机制：

式中：，rand为[0,1]均匀分布的随机数；r(=1，2，3)为随机个体索引；best表示当前种群中动态更新的最优个体；F和F分别为DE/rand/1/bin和DE/best/1/bin这2种变异机制的变异常数；min和max分别为选择变异机制DE/rand/1/bin的最小和最大概率；为当前进化代数；为最大进化代数。由式(12)可知：在进化前期，变异机制DE/rand/1/bin被更多地采用，有效地保证了种群的多样性，使算法具有较强的全局搜索能力，从而尽可能多地找到潜在全局最优点。随着进化代数增加，变异机制DE/best/1/bin被选择的概率不断增加，算法的局部搜索能力逐步增强，加快了收敛速率，同时也提高了算法精度。

4.2 交叉操作

DE通过将当前个体()对应变异个体()进行交叉，生成试验个体() =(u1,u2, …,u)，从而提高种群的多样性。

其中：=1，2，…，；C为交叉概率常数。DE/rand/1/bin和DE/best/1/bin这2种变异机制的交叉概率常数分别用C和C表示。

4.3 选择操作

DE算法基于贪婪的选择方式，对测试个体()以及当前个体()选择更优的个体进入下一代搜索。以最小化问题为例，其选择策略为

5 算法流程

综合以上双层规划问题的单层转化方法和混合罚函数的约束处理方法，本文提出的自适应变异DDE算法求解上述双层规划问题的算法流程如下。

Step 1：将相应的双层规划问题按照式(2)转化成式(3)这种单层规划问题，列出所有的不等式约束和等式约束。

Step 2：给定DDE种群规模NP、差分变异矢量收缩因子F和F、交叉概率常数C和C，在每个变量的定义域内随机初始化每个个体，设置最大迭代次数，置当前迭代计数器=0。

Step 3：按式(8)~(10)计算个体对各个不等式约束的惩罚因子，并确定精确罚函数的惩罚力度。

Step 4：按照式(6)和(11)得到每个个体对应的惩罚因子1和2。

Step 5：按式(5)计算每个个体对应的上层规划目标函数的适应值，求出相对应的最优适应值best和最优个体best。

Step 6：判断1和2是否达到精度要求或者进化代数是否达到所设定的最大进化代数，若是，则终止；否则，执行下一步。

Step 7：对种群中的个体()执行Step 7~Step 10，生成+1代种群。

Step 8：在种群中随机选取3个与()不同的个体，按照式(12)和(13)进行变异操作，生成变异个体。

Step 9：按照(14)式进行交叉操作，生成实验个体u()。

Step 10：按照式(15)进行选择操作，生成+1代个体X(+1)。

Step 11：=+1，返回Step 3。

6 数据分析

6.1 测试函数

为了证明算法能有效解决该类双层规划问题，选取8个测试问题进行数值仿真实验。各测试问题的定义如下。

1) TP1：

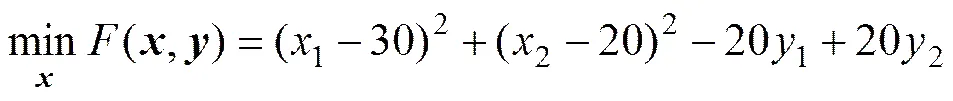
subject to

。

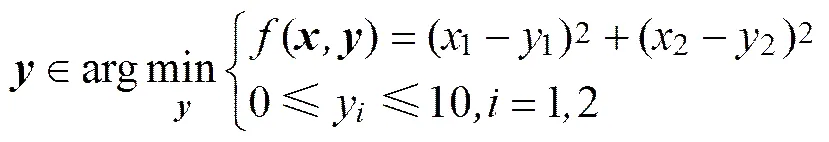
2) TP2：

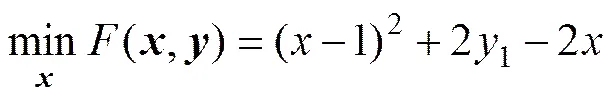
subject to

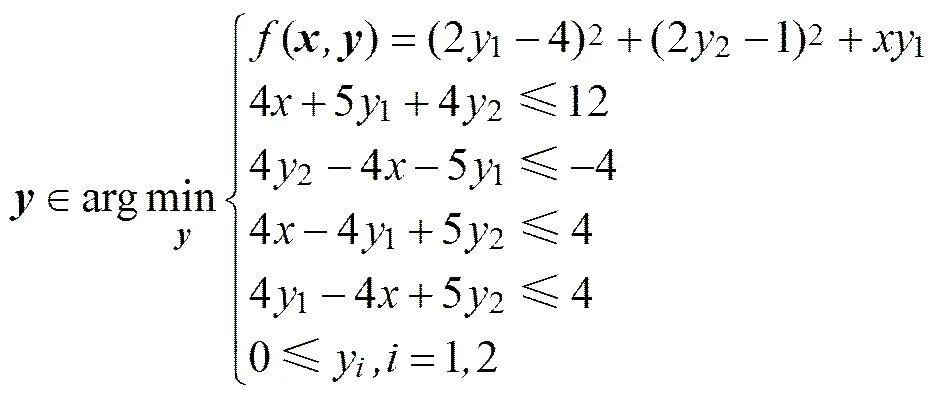
0≤。

3) TP3：

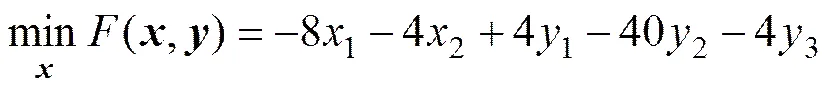
subject to

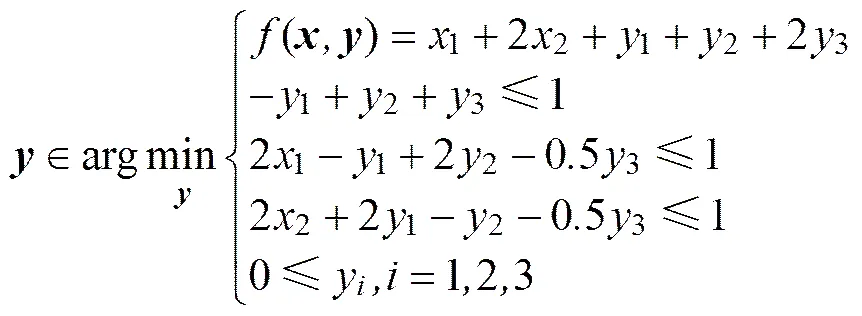
4) TP4：

subject to

0≤≤1。

5) TP5：

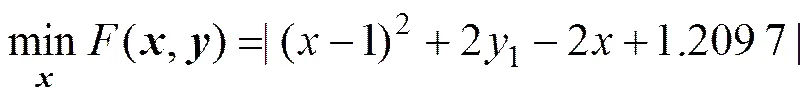
subject to

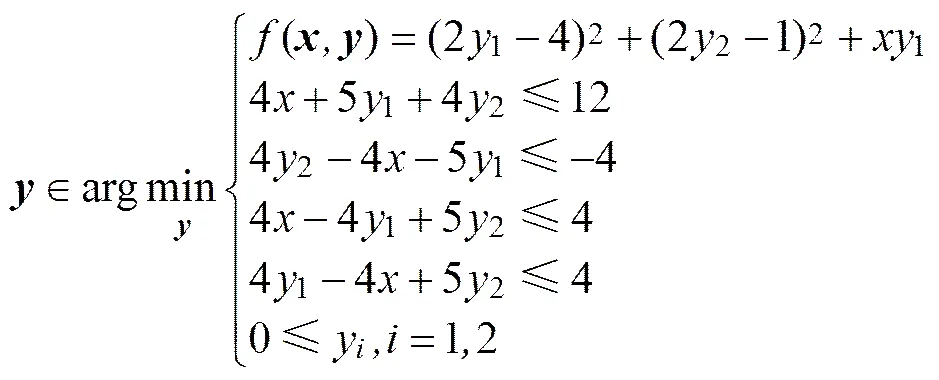
6) TP6：

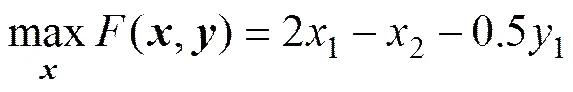
subject to

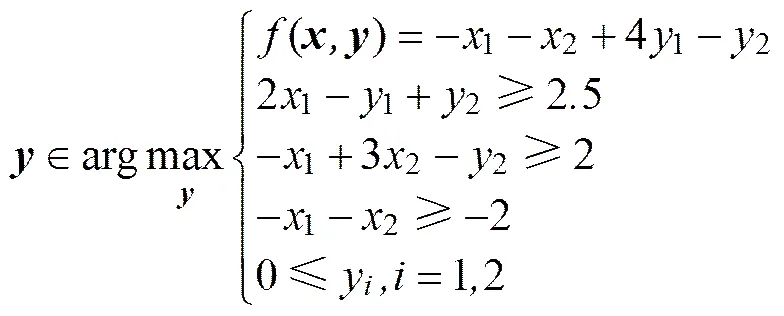
0≤x，=1，2。

7) TP7：

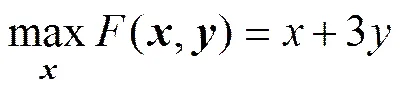
subject to

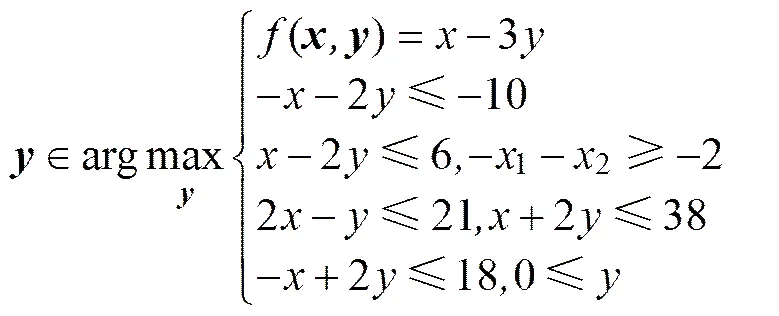
0≤。

8) TP8：

subject to

0≤≤8。

6.2 测试结果及分析

实验中，SADDE算法的参数设置如下：种群规模N=50，最大进化代数=200，2种变异机制选择相同的变异常数F=F=0.5，自适应变异策略中DE/rand/1/bin策略的最小和最大选择概率min=0.1和max=0.8。对于交叉概率常数，为了突出DE/rand/1/bin的全局搜索能力，选取较小的C以保持种群的多样性，设置C=0.1。为了突出DE/best/1/bin的局部开发能力，选择较大的C以提高收敛速率和精度，设置C=0.9。为了避免随机性影响，SADDE对每个测试问题独立运行20次，取最好值为全局最优解，如表1所示[17−21]。为了验证本文方法的有效性，表1给出了与现有文献其他算法包括遗传算法(NEA，GA，BIGA，AGA，SMGA，PFGA)、禁忌搜索算法(TS)以及差分进化算法(BIDE，DEBLP)等对所选测试问题的最好计算结果。表1中，(,)和(,)分别表示上层和下层目标函数值。

表1 测试函数计算结果

由表1可知：本文方法能够求得以上所有问题的全局最优解，且所求得解完全满足约束条件。由于使用KKT条件将双层问题转化为单层问题，使得维数变多(增加了算子)，而SADDE的参数设置较少，故相对于采用KKT条件的其他算法(包括NEA和BMA等)避免了计算过程中一些参数的反复调试，因此，收敛速度较快且更精确。而相对于BIDE，SADDE由于KKT条件的引入和高效约束处理，在计算复杂度上要远比采取嵌套机制的BIDE低。此外，种群的动态更新和自适应变异机制使得SADDE具有更快的收敛速率和更高的收敛精度。表2所示为SADDE与NEA求解问题 P1~P5时所用平均CPU时间比较。由表2可知：SADDE的收敛速度明显要快于NEA，是一种求解该类双层规划问题时的有效算法。

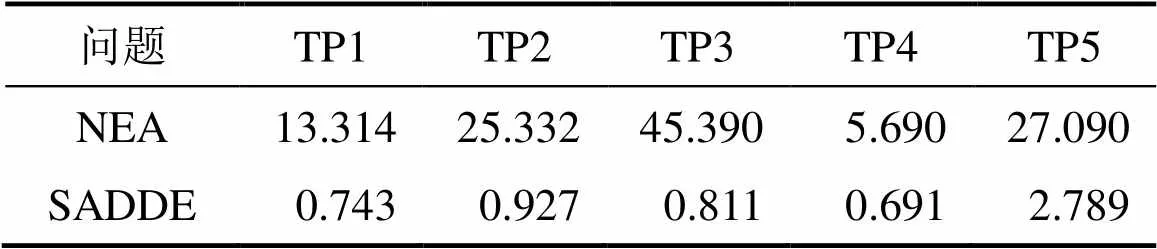
表2 NEA[15]与SADDE平均CPU计算时间

实验中，对于TP3，TP7和TP8，尽管GA[21]和DEBLP[22]取到了更好的上层结果，但对于TP3，按照文献[21]，若上层变量均取0，则要满足下层目标函数取最小值，下层变量的取值应当均为0，而并非文献[21]中给出的(1.5,1.5,1)；若和均取0，反而得到更差的上层解。因此，尽管文献[21]中取得了更好的上层结果，但事实上该最优解(0,0,1.5,1.5,1)是1个不可行解，其违反了双层规划中下层函数对上层函数的约束。同理，对于TP7和TP8，GA和DEBLP均获到了更好的上层结果，但其解也是1个不可行解，因此，这2种方法在求解该类问题时不能保证约束满足。而SADDE不存在此类问题。

此外，为证明自适应变异算子的有效性，给出SADDE与DE/rand/1/bin和DE/best/1/bin求解上述8个测试问题20次独立运行求得的平均最优适应度，如图1~8所示。由图1~8可知：对于测试问题TP1，TP2，TP5和TP8，SADDE均能较快地找到全局最优解；对于测试问题TP3，TP4，TP6和TP7，尽管DE/best/1/bin收敛速度很快，但均陷入局部最优，而DE/rand/1/bin速度较慢，在迭代次数较少时难以收敛到全局最优解。因此，SADDE综合了DE/rand/1/bin和DE/best/1/bin这2种变异机制的优点，既能有效地保持种群的多样性，又具有较快的全局收敛性能，使算法在全局最优解的探索和局部最优解的开发之间达到很好的平衡，是一种求解复杂非线性约束优化问题的有效方法。

1—SADDE；2—DE/rand/1；3—DE/best/1。

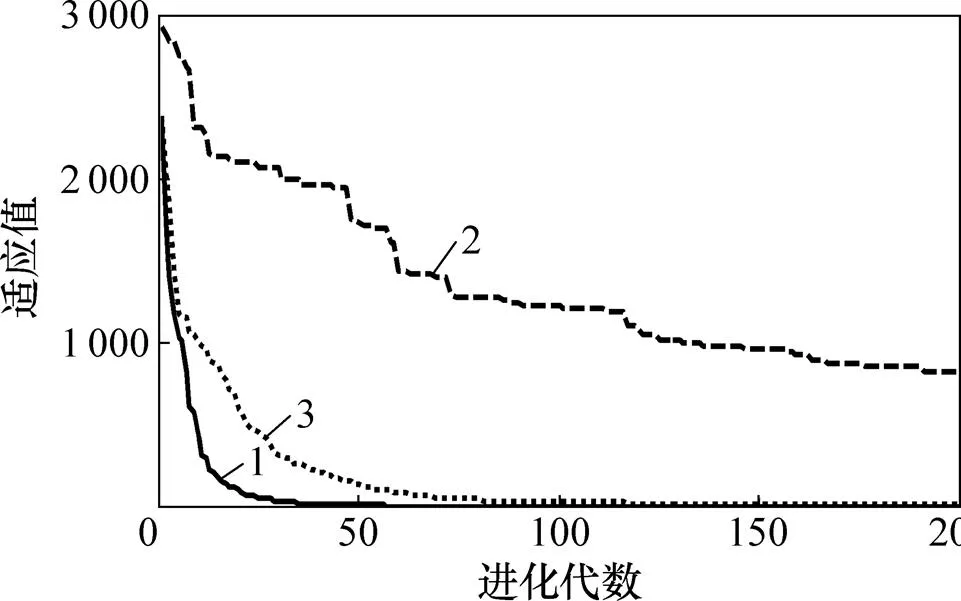
1—SADDE；2—DE/rand/1；3—DE/best/1。

1—SADDE；2—DE/rand/1；3—DE/best/1。

1—SADDE；2—DE/rand/1；3—DE/best/1。

1—SADDE；2—DE/rand/1；3—DE/best/1。

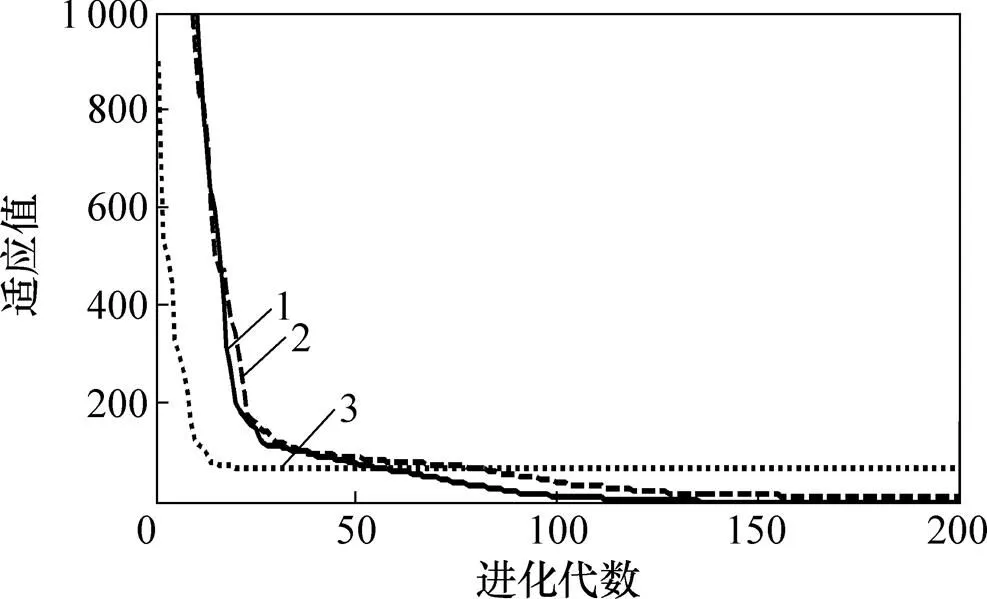
1—SADDE；2—DE/rand/1；3—DE/best/1。

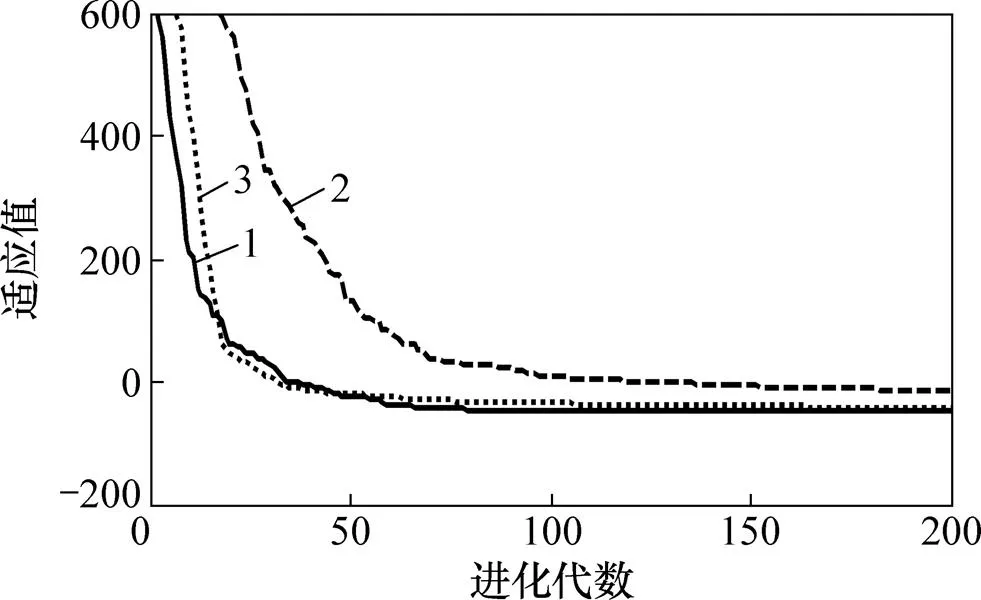
1—SADDE；2—DE/rand/1；3—DE/best/1。

1—SADDE；2—DE/rand/1；3—DE/best/1。

7 结论

1) 针对一类下层函数可微且凸的非线性双层规划问题，通过KKT条件将双层规划问题转化为非线性约束单层规划问题。对于不等式约束和等式约束，分别采用非固定多段映射罚函数法和精确罚函数法对约束进行处理，将原非线性双层规划问题转化为系列无约束单层非线性优化问题。

2) 提出一种自适应变异动态差分进化算法对该问题进行求解。动态差分进化算法采用动态更新种群方式，对于任一目标个体，若新生成的试验矢量比其具有更优的适应度，则试验矢量替代目标矢量且立即加入当前种群并参与其后的进化操作，这样大大提高了算法的收敛速率。自适应动态变异机制结合了DE/rand/1/bin全局搜索能力强和DE/best/1/bin局部开发能力强的优势，提高了算法的收敛性能和鲁棒性。

3) 本文所提出的方法能够求得该类非线性双层规划问题的全局最优解，具有良好的收敛性能和鲁棒性，且相对于NEA，平均CPU时间大幅度缩短，证明了SADDE的计算高效性。

4) SADDE的自适应变异机制相对于DE/rand/1和DE/best/1机制能够获得更好的收敛效果，证实了自适应算子的学习能力和平衡算法性能的作用。因此，SADDE是一种求解该类非线性双层规划问题的有效方法。

参考文献：

[1] VICENTE L N, CALAMAI P H. Bilevel and multilevel programming: a bibliography review[J]. Journal of Global Optimization, 2004, 5(3): 291−306.

[2] COLSON B, MARCOTTE P, SAVARD G. An overview of bilevel optimization[J]. Annals of Operational Research, 2007, 153(1): 235−256.

[3] HANSEN P, JAUMARD B, SAVARD G. New branch and bound rules for linear bilevel programming[J]. SIAM Journal on Science and Statistical Computing, 1992, 13(5): 1194−1217.

[4] VICENTE L, SAVARD G, JUDICE J. Decent approaches for quadratic bilevel programming[J]. Journal of Optimization Theory and Applications, 1994, 81(2): 379−399.

[5] WANG Guangmin, WANG Xianjia, WAN Zhongping, et al. An adaptive genetic algorithm for solving bilevel linear programming problem[J]. Applied Mathematics and Mechanics, 2007, 28: 1605−1612.

[6] RAJESH J, GUPTA K, KUSUMAKAR H, et al. A tabu search based approach for solving a class of bilevel programming problems in chemical engineering[J]. Journal of Heuristics, 2003, 9: 307−319.

[7] WANG Yuping, JIAO Yongchang, LI Hong. An evolutionary algorithm for solving nonlinear bilevel programming based on a new constraint-handling scheme[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part C, 2005, 35: 221−232.

[8] 李昌兵, 杜荗康, 付德强. 基于层次粒子群算法的非线性双层规划问题求解策略[J]. 系统工程理论与实践, 2013, 33(9): 2292−2298. LI Changbing, DU Shukang, FU Deqiang. Solution strategy for bi-level nonlinear programming problem based on hierarchical particle swarm optimization[J]. Systems Engineering: Theory & Practice, 2013, 33(9): 2292−2298.

[9] LI Hecheng, LEI Fang. An evolutionary algorithm for solving bilevel programming problems using duality conditions[J]. Mathematical Problems in Engineering, 2012, 20: 1101−1114.

[10] JAQUELINE S A, EDUARDO K, HELIO J C B. Differential evolution for bilevel programming[C]//2013 IEEE Congress on Evolutionary Computation, 2013: 470−477.

[11] STORN R, PRICE K. Differential evolution:a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341−359.

[12] DAS S, SUGANTHAN P N. Differential evolution:a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4−31.

[13] QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398−417.

[14] 吴亮红, 王耀南. 动态差分进化算法及其应用[M]. 北京: 科学出版社, 2014: 81−88. WU Lianghong, WANG Yaonan. Dynamic differential evolution algorithm and its application[M]. Beijing: Science Press, 2014: 81−88.

[15] 王宇平. 进化计算的理论和方法[M]. 北京: 科学出版社, 2011: 169−190. WANG Yuping. The theory and methods of evolutionary computation[M]. Beijing: Science Press, 2011: 169−190.

[16] BARD J F. Pratical bilevel optimization[M]Norwell: Kluwer, 1998: 1−50.

[17] SHIMIZU K, AIYOSHI E. A new computational method for Syackelberg and min-max problems by use of penalty method[J]. IEEE Transactions on Automatic Control, 1981, 26(2): 460−466.

[18] WANG Guangmin, WANG Xianjia, WAN Zhongping, et al. Genetic algorithms for solving linear bilevel programming[C]// Proceedings of the Sixth International Conference on Parallel and Distributed Computing Applications and Technologies. Washington DC, USA: IEEE Computer Society, 2005: 920−924.

[19] ODUGUWA V, ROY R. Bi-level optimization using genetic algorithm[C]//Proceedings of IEEE Int Conf Artificial Intelligence Systems, 2002: 123−128.

[20] 张蕾. 求解一类特殊非线性双层规划问题的进化算法[D]. 西安: 西安电子科技大学计算机学院, 2010: 21−29. ZHANG Lei. Evolutionary algorithms for one special class of nonlinear bilevel programing problem[D]. Xi’an: Xi’an Electronic and Science University. School of Computer Science and Technology, 2010: 21−29.

[21] KOH A. Solving transportation bi-level programs with differential evolution[C]//2007 IEEECongress on Evolutionary Computation, 2007: 2243−2250.

(编辑 陈灿华)

A self-adaptive mutation dynamic differential evolution algorithm for a class of bi-level programming problem

WU Lianghong, XU Rui, ZUO Cili, ZEN Zhaofu, DUAN Weitao

(School of Information and Electrical Engineering,Hunan University of Science and Technology, Xiangtan 411201, China)

Considering aclass of nonlinear bi-level programmingproblem withnon-convex and non-differentiable upper-levelfunction and constraints, convex and differentiablelower-level function and constraints was studied. The Karush-Kunh-Tucker (KKT)conditions were firstly used to transform the bi-level programming problem intoa single-leveloptimization problem. Then, the non-fixedmulti-segmentmappingpenalty function andfixedpenalty function methods were combined to deal with theconstraints. Thereafter, an improved dynamicdifferential evolution algorithm was proposed to solvethe sequence non-constraint problems. Eight benchmarks problems were used to test the proposed method. The results show that, the proposed method is veryeffective for solving such class of bi-level programming problem compared with other algorithms.

bi-level programming; KKT conditions; penalty function method; differential evolution algorithm

10.11817/j.issn.1672-7207.2016.10.021

TP18

A

1672−7207(2016)10−3436−09

2015−11−20；

2016−01−15

国家自然科学基金资助项目(61203309，51374107，61403134)；湖南省教育厅优秀青年基金资助项目(12B043)；湖南省研究生科研创新项目(CX2015B488)(Projects(61203309, 51374107, 61403134) supported by the National Natural Science Foundation of China; Project(12B043) supported by Education Department of Outstanding Youth Foundation of Hunan Province; Project(CX2015B488) supported by Innovation Foundation of Hunan Province For Postgraduate)

吴亮红，博士，副教授，从事智能优化算法、多目标优化、智能控制理论及应用研究等；E-mail: lhwu@hnust.edu.cn