一种新的可变数目机动目标联合检测与跟踪算法

胡秀华，郭雷，李晖晖，燕攀登



一种新的可变数目机动目标联合检测与跟踪算法

胡秀华，郭雷，李晖晖，燕攀登

(西北工业大学自动化学院，陕西西安，710129)

在低信噪比多传感器观测环境下，针对机动目标数目变化时跟踪性能不高的问题，提出一种新的目标联合检测与跟踪算法。依据粒子存在变量进行预测状态粒子集的采样，考虑状态粒子集与当前观测值的关联程度，利用模糊拍卖算法与粒子群优化理论解决状态集与观测集之间的关联问题，并给出目标出现与消失的判定准则，实现粒子权值更新；依据混合采样方法得到包含模型信息和状态信息的粒子集，并按照目标模型概率进行粒子状态融合得到目标局部状态后验估计值和均方误差；最后，对关联的各传感器局部航迹信息进行加权融合，得到各目标的全局状态估计值，并与经典多模粒子滤波算法的仿真试验对比分析。研究结果表明：新算法在运动模型概率估计、状态估计及目标数目估计方面具有有效性。

多模粒子滤波；检测与跟踪；关联判定；目标；混合采样

现代防空系统需要借助于多传感器提供的互补观测信息进行探测工作，复杂的观测环境对机动目标跟踪算法也提出了越来越高的要求。传统的先检测后跟踪算法大多先对传感器每帧原始数据进行门限检测，然后利用超过门限值的测量数据进行跟踪处理。这种方法虽然在一定程度上减少了计算量，但是损失了许多有用信息。为了提高目标的检测与跟踪性能，利用未经门限处理的多帧原始观测数据进行能量积累，以实现融合检测与跟踪的算法受到了广泛关注[1]。典型的检测与跟踪算法包括基于Hough变换的算法，动态规划算法、极大似然估计以及粒子滤波算法等。其中，基于粒子滤波实现的递归算法得到了广泛的改进与研究应用[2]。多模粒子滤波算法利用粒子滤波实现对各粒子加权求和得到状态估计，然后依据多模型中每个模型的模型概率对各模型的估计值加权求和，得到多模型粒子滤波器的全局估计值，该方法通常是在所采用的滤波器完成对状态估计的同时，进行实时系统模型估计，适用于机动目标跟踪[3−4]。关于经典多模粒子滤波算法的改进方法大致涉及粒子重要性采样、重采样、模型概率以及滤波框架4类。DAVEY等[5]在基于两级采样的粒子滤波算法基础上，采用边缘粒子滤波过程进行持续粒子采样，改善了状态采样的多样性，为多模粒子滤波算法提供了思路。王晓 等[6]给出了基于混合采样的多模型粒子滤波算法单机动目标跟踪，计算复杂度与单模型粒子滤波算法相当，算法运行效率高。吴瑕等[7]给出了一种混合估计多模粒子滤波算法，并对重采样步骤进行了改进，提出的序贯重要性平滑重采样策略可以有效提高粒子多样性，文中虽然考虑了目标是否存在的模型变量，但是没有给出目标数目变化的判定方法。WANG等[8]针对距离模糊雷达的单目标跟踪问题，在扩维的目标状态矢量中增加了表示目标是否存在以及表征脉冲间隔数的变量，提出的混合多模粒子滤波方法有效改善了目标跟踪性能，但有待于进一步研究多目标存在的情况。鉴福升等[9]通过将模型估计和状态估计分开计算，利用模型似然函数计算模型后验概率，可以用较小的粒子总数获得较好的跟踪性能，减小了计算量。针对包含连续状态变量和离散状态变量的随机混合系统，YANG等[10]给出了一种基于新息误差的反馈式多模粒子滤波算法结构，并运用在了角度测量传感器的单目标跟踪中，但是该方法与标准多模粒子滤波算法的目标跟踪性能及算法复杂度对比方面还有待于进一步研究。总之，现有算法虽然在一定程度上解决了粒子多样性及算法计算量问题，但是大多没有考虑实际多传感器观测环境下机动目标数目变化时的跟踪情况，并且忽视了对状态粒子集与当前观测值的关联判定，降低了目标跟踪性能。针对上述问题，本文作者在多模粒子滤波的框架基础上，提出一种新的目标联合检测与跟踪算法。首先进行初始化设置，获得初始时刻的粒子集；在粒子状态预测与更新步骤中，依据粒子存在变量进行预测状态粒子集的采样，考虑状态粒子集与当前观测值的关联程度，利用模糊拍卖算法与粒子群优化理论解决状态集与观测集之间的关联问题，并给出目标出现与消失的判定准则，实现粒子权值更新；利用序贯重要性采样理论对混合采样粒子集进行重采样，得到包含模型信息和状态信息的粒子集；考虑粒子存在变量的影响，按照目标模型概率进行粒子状态融合得到目标局部状态后验估计值和均方误差；最后，对关联的各传感器局部航迹信息进行加权融合，得到各目标的全局状态估计值，并最终求得机动目标数目的估计值。通过与经典多模粒子滤波算法的仿真试验对比分析，验证了本文给出的新算法的有效性。

1 系统建模

在多传感器公共探测区域内，考虑在时刻有个目标(其中，=1，2，…；=0，1，…，max；max为目标可能存在的最大数目)。令表示目标的状态，表示目标在时刻接收到的传感器S的量测数据(=0，1，…，；传感器编号为=1，2，…，；为传感器最大数目)。

1.1 目标运动模型

在笛卡儿坐标系内，假设目标在−平面内作机动运动，在时刻，选取目标状态变量为

系统模型状态间转换概率可表示为

其中：=1，2，3；=1，2，3；表示系统模型由−1时刻的状态转换为时刻的状态的概率，系统模型间概率转移矩阵可记为，且满足；=1，2，3。

其中：1−P为新目标在场景中不存在的概率；1−P为目标继续在场景中存在的概率。

1.2 传感器观测模型

假设多传感器系统由雷达和红外组成，在极坐标系下给出各传感器S的观测模型[11−12]。

对于雷达传感器系统，假设雷达在探测区域的原始观测数据为基于信号功率强度的距离−多普勒−方位图像，设定每帧图像有N×N×N个分辨单元，每个分辨单元可表示为(，，)(=1，2，…，N；=1，2，…，N；=1，2，…，N；N，N和N分别为功率测量单元中距离、多普勒和方位角单元的数目)。在时刻，对于单个目标，雷达传感器在分辨单元(，，)的量测数据,k可以表示为每个分辨单元接收信号功率的集合，即

其中：A表示目标的复幅度；为用以计算各分辨单元目标回波强度的函数；为分辨单元中的复量测噪声。

对于有多个目标存在的情况，雷达的接收信号功率为多个单目标功率值的叠加。

对于红外传感器系统，假设传感器在探测区域的原始量测为序列灰度图像。设定每帧观测图像有N×N个分辨单元，若每个分辨单元可表示为(，)(其中，=1，2，…，N；=1，2，…，N)，分辨单元大小为Δ×Δ，则在时刻，对于单个目标，红外传感器量测数据可以表示为

根据目标是否存在，依据目标接收信号强度，分辨单元(，)内的观测数据表示为

对于有多个目标存在的情况，红外传感器的接收信号强度为多个单目标幅值的叠加。

2 一种新的目标联合检测与跟踪算法的实现

2.1 算法的提出与改进思路

在多模粒子滤波的框架基础上，提出一种新的分布式目标联合检测与跟踪算法。该算法利用模糊拍卖算法与粒子群优化理论求得状态粒子集与当前观测值的关联程度，给出目标出现与消失的判定准则，并依据混合采样方法得到包含模型信息和状态信息的粒子集，实现对目标运动模型及状态变化的准确估计。设计的新算法能够在判定状态粒子集与传感器观测值的关联性基础上，依据目标存在状态、模型概率等先验信息更准确地完成粒子状态预测及更新，可以有效处理跟踪期间目标相距较近以及目标数目发生变化的情况，最终实现目标融合状态估计，适合于目标数目发生变化时的多传感器多目标跟踪场景。新算法的分布式融合估计结构原理如图1所示，其中和为单传感器S输出的状态局部估计信息，和为状态全局融合估计信息。

2.2 结合模糊拍卖算法与粒子群优化理论的状态粒子集与观测集的关联判定

在杂波环境下，为有效地进行多目标状态粒子集更新，需要先将当前的观测值与每个目标的状态粒子集进行数据关联判定。为避免穷举搜索，利用动态二维分配思想解决观测与航迹之间的关联问题，以观测与航迹的模糊统计距离为代价，构建观测值−状态粒子集二维分配问题的数学模型；利用模糊理论与拍卖算法相结合，将模糊代价矩阵转换为拍卖算法中的利益矩阵，将求解最小代价问题转化为拍卖算法中的求解利益最大问题[13]，同时，由于在低信噪比环境中，干扰量测较多，拍卖算法的优化搜索效率较低，引入粒子群优化理论进行全局搜索[14]，最后得出目标状态粒子集与传感器观测集的关联性判定结果。

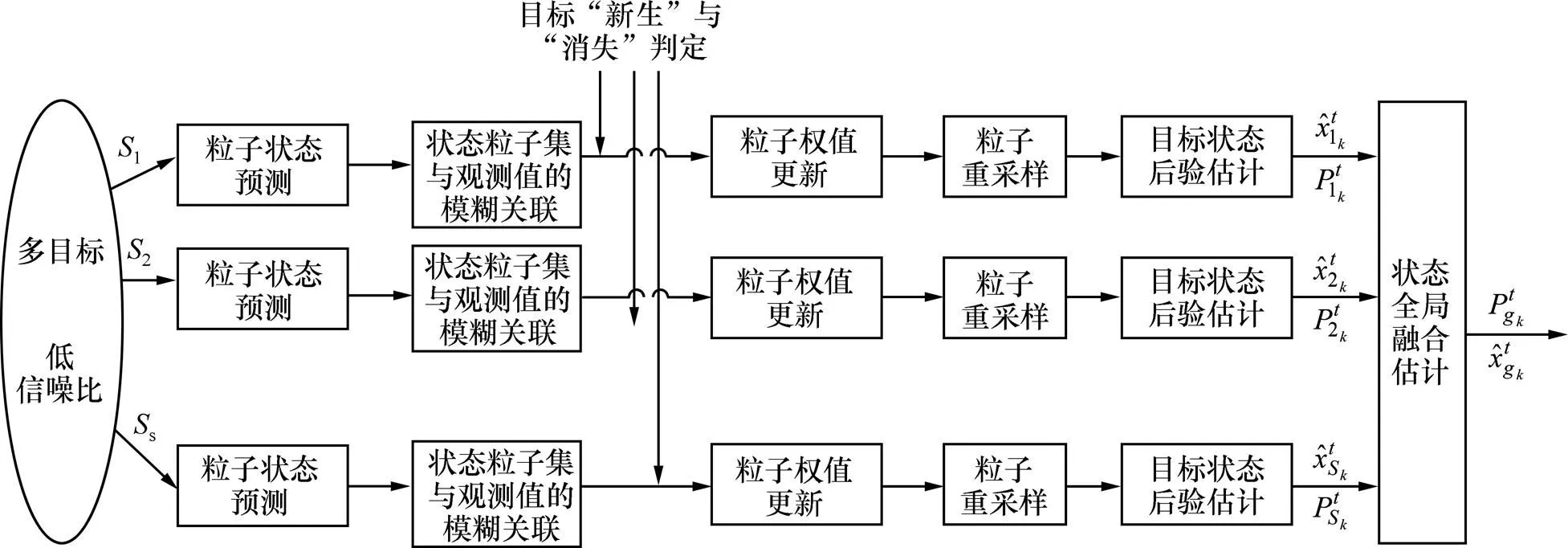
图1 分布式融合估计结构原理

定义二进制决策变量为

则观测值−状态粒子集二维分配问题的数学模型可表示为式(10)~(13)，即

约束条件为

其中：式(10)为目标函数；式(11)表示每一个观测有唯一的源；式(12)表示1个给定目标最多有1个观测以其为源，式(13)表示第个观测值与第个目标状态粒子集是否关联，1为相关，0为不相关。上述分配问题的最优解可表示为每行、每列最多只有1个1的阶关联决策矩阵。

依据拍卖算法的价格定义，对每一个可能与状态关联的观测值，计算竞拍价格

其中：1为利益系数，2为代价系数，且有1+2=1，为足够小的正数。对于阶竞拍价格矩阵，价格元素的行序号对应观测值编号，列序号对应状态编号。

则最优适应度对应的竞拍价格即为全局最优值，相应粒子位置表示目标状态粒子集与传感器观测值的最优关联结果。

2.3 一种新的目标联合检测与跟踪算法步骤

文中设计的基于多模粒子滤波器的联合检测与跟踪算法主要包括粒子状态预测、状态粒子集与当前观测值的模糊关联判定、粒子权值更新、重采样、目标局部状态后验估计、目标全局状态融合估计，新算法的一次迭代步骤如下。

1)初始化。

在传感器S观测下，对于目标，在=0时刻，粒子以初始模型概率为基础进行混合抽样，根据被估计状态变量初值抽取个采样粒子，假定目标初始时刻状态分布为，模型概率为，记采样控制变量为()，其中，当满足

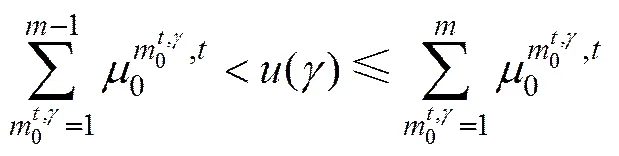
时，则认为该时刻第个粒子所对应的采样模型状态为，此时，抽取采样粒子，相应粒子权重取，最后得初始粒子集(其中，，和分别表示时刻目标的采样粒子所对应的运动状态、采样模型状态及相应权值，=1，2，…，为粒子数；为采样粒子总数；，为模型总数)。

2)粒子状态预测。

在−1时刻(=1，2，…)，记表征目标混合状态后验分布的粒子集为。在预测粒子状态时，分3种情况进行处理。

3)状态粒子集与观测值的模糊关联。

4)粒子权值更新。

处理好粒子与观测之间的关联性，并完成状态粒子集更新后，对每个粒子进行权值更新，并对得到的粒子权值进行归一化处理。为了克服标准粒子滤波中仅由量测概率密度函数求得粒子权值所包含的信息量少的缺陷，对应于不同的粒子存在状态，可以借助似然比公式进行求解[8]，并依据文献[5]中的采样集合混合理论合并个粒子，得混合粒子集(其中，=，，=1，2，…，)。

5)重采样。

6)目标局部状态估计。

单纯的将所有粒子的位置和权值进行加权平均求得的目标状态估计会有较大误差，这里考虑粒子存在变量的影响，按照每个模型的模型概率进行状态粒子融合可以得到目标局部状态后验估计值和均方误差。

则状态后验估计为

估计均方误差为

在时刻，目标存在的后验概率为

P(19)

则依据目标存在概率表达式，可得到时刻目标数目的局部估计值为

其中：Round()表示求得距离最近的整数。

因此，在观测时间序列=1，2，…，内，对于传感器S，目标的子航迹可表示为状态集合，时刻估计出的目标数目为。

7)目标全局状态估计。

假设各传感器之间已实现时空同步处理，各个传感器信息处理系统之间的过程噪声、量测噪声互不相关。由于步骤3已初步实现量测−航迹关联的判定，对于多传感器之间的子航迹信息，类似于步骤3中提及的模糊关联理论，可采用基于模糊关联矩阵的二维分配方法进行精关联判定，完成各传感器局部航迹信息之间的关联问题求解。因此，对于目标，参照分布式融合结构，在信息融合中心对各传感器输出的目标子航迹信息进行加权融合可得

全局状态估计值为

全局状态估计均方误差为

在各时刻，观测场景中的目标数目估计值为各传感器局部估计值中的最大值，即

文中设计的多模型粒子算法，其采样过程中使用了一定的先验信息和前一时刻的后验信息，通过对多模型混合采样得到目标状态后验分布粒子集，保证了粒子多样性；算法引入了状态粒子集−观测值之间以及各传感器子航迹信息之间的关联判定，并按照每个模型的模型概率进行融合得到的多模型粒子滤波器的估计值，提高了状态估计信息的准确性。

3 仿真与分析

为简化问题，在二维监视区域内，假设多传感器系统由1部雷达和1台红外探测器组成；假设其采样时间同步，且已完成坐标转换与时间对准；设定所有目标在传感器观测的重合区域内机动。假设观测时间为150 s，在整个观测期间，共有3个目标出现和消失，目标在场景中出现的时间段及相应运动状态如表1所示。用于算法测试的硬件环境是因特尔酷睿双核处理器、2.10 GHz主频、2.0 GB内存、1.0 GB显卡，软件环境是Windows 7，Matlab R2012b。

设定目标1的初始位置为[10 500，8 000] m，初始速度为[50，180] m/s；目标2的初始位置为[12 500，15 300] m，初始速度为[154，115] m/s；目标3的初始位置为[12 100，9 300] m，初始速度为[155，88] m/s；3个目标机动转弯均采用转弯速率0.06 rad/s和0.07 rad/s。

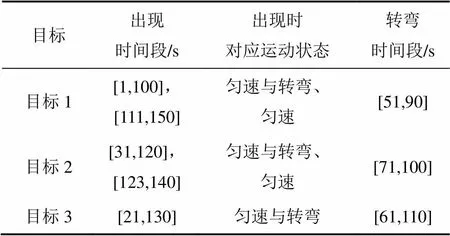
表1 目标出现的时间段及相应运动状态

为了计算方便，设公共观测区域为[10 000，27 000] m×[4 000，21 000] m的观测空间，对于雷达传感器1，目标的距离单元均匀分布在[13 000，30 000] m，多普勒单元均匀分布在[−125，200] m/s，考虑只有1个方位单元的情况，分辨单元数目设为340×50×1，距离分辨率单元为50 m，多普勒分辨率单元为 6.5 m/s，扫描间隔为1 s，假设3个目标所在的初始距离−多普勒分辨单元为依次为(5，43)，(137，48)和(49，48)。对于红外传感器2，灰度图像在2个方向上的距离分辨单元均为100 m，分辨单元数目为170×170，扫描间隔为1 s，假设3个目标初始位置依次为(5，40)，(26，114)和(23，54)，速度依次为(0.5，1.8)，(1.53，1.11)和(1.65，0.92) 个/s。

为验证本文算法的有效性，使用其他2种滤波方法对场景中的机动目标进行跟踪，算法一为文献[15]中的经典多模粒子滤波算法，算法二为文献[16]中的一种改进多模型粒子滤波算法。在各多模型算法中，均使用CV(constant velocity)模型和CT(constant turn)模型，各模型的状态转移函数表达式及过程噪声协方差的选取见文献[17]。

由Matlab2012b仿真得出，观测场景中目标的运动轨迹，如图2所示。从图2(b)可看出各目标在不同时刻的存在状态及相互关联程度。

若观测场景信噪比取为8 dB，取雷达传感器观测噪声标准差为0.6，红外传感器观测噪声标准差为2.6，依据目标信噪比公式及相关参数的经验值，可知目标由雷达传感器获得的回波功率信息大约为4.5，目标由红外传感器获得的回波信号强度信息大约为6.5。对于雷达传感器，在=15时，只有1个目标，位于分辨单元(46，43)处；在=65时，有3个目标，分别位于分辨单元(198，43)、(260，48)和(211，47)处；在=105时，有2个目标，分别位于分辨单元(323，16)和(229，12)处。对于红外传感器，在=15时，目标位于分辨单元(12，65)处；在=65时，3个目标分别位于分辨单元(42，141)、(77，151)和(96，91)处；在=105时刻，2个目标分别位于分辨单元(130，139)和(129，47)处。不同时刻雷达传感器观测情况如图3(a)~3(c)所示，红外传感器观测情况如图3(d)~3(f)所示。

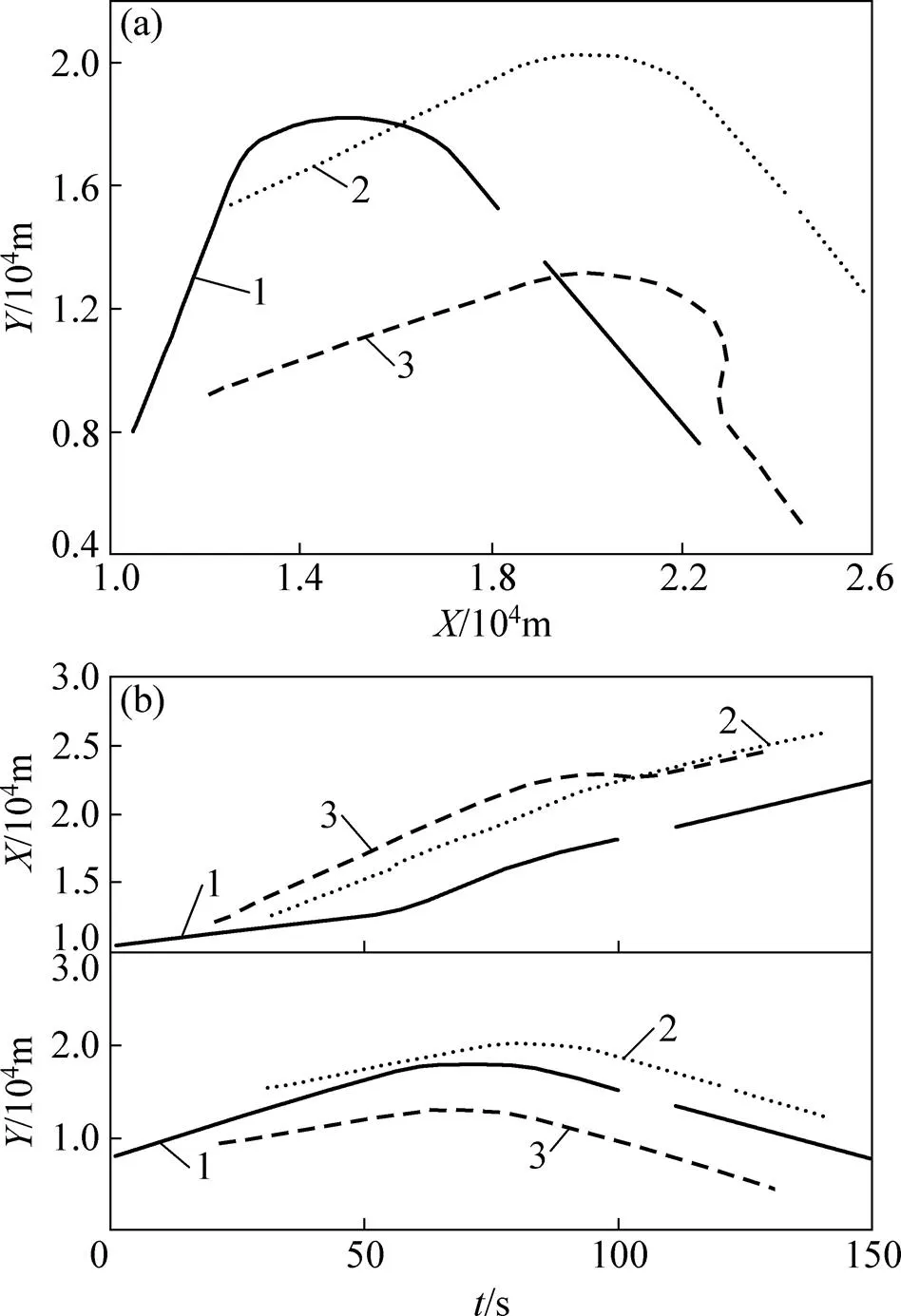
(a) 二维空间；(b)一维空间1—目标1；2—目标2；3—目标3。

由图3(a)和3(d)可知：受杂波及传感器观测模糊的影响，目标信号均淹没于噪声中；由图3(b)和3(e)，3(c)和3(f)可知：当目标相距较近时，回波观测数据相互影响，很难直接从单帧观测图中直接检测出目标。因此，在信噪比较低的多目标跟踪环境中，有必要研究考虑目标状态与观测数据关联的多传感器联合检测与跟踪算法，利用帧间能量积累提高信噪比，并利用各传感器互补信息提高目标检测与跟踪的精度。

为更好地验证各算法性能，在信噪比SN分别为8 dB和3 dB的情况下，对于各时刻各机动目标，经过100次Monte Carlo仿真，图4和图5所示分别为不同算法对于典型目标1和2的模型概率估计，图6和图7所示为不同算法对于各目标的运动状态估计误差，图8所示为不同算法对于目标数目的估计。

k：(a) 15；(b) 65；(c) 105；(d) 15；(e) 65；(f) 105

由图4和图5可以看出：在相同信噪比条件下，在对典型目标运动模型的估计准确性方面，本文算法要比算法一和算法二更优；随着信噪比降低，各算法的运动模型概率估计准确性均有所下降，但是本文算法的估计性能变化不大且明显比算法一和算法二的优。这是由于本文算法采用了状态粒子集与观测值的关联判定，当目标相距较近以及出现运动模型切换时，该算法能快速判定粒子集与观测值的关联度，使得多模型粒子滤波方法可以更有效地估计目标运动模型的概率，估计效果更接近目标运动的真实模型。当目标数目发生变化时，本文算法所采用的软判定准则不能及时判定出目标数目变化，在一定程度上影响了运动模型估计精度，但是变化间隔越短所受影响越小；而算法一和算法二的硬性判定虽然可以相对快速地检测到目标数目变化，但在低检测率场景中，缺乏粒子集与观测值的关联判定会影响目标数目的准确估计，进而导致目标运动模型的错误估计。

从图6和图7可以看出：在相同信噪比条件下，在运动状态误差估计方面，本文算法要优于算法一和算法二；当目标相距较近、运动模型切换或者信噪比降低时，估计误差均会增大，但是本文算法能更快地将误差收敛到平稳状态，跟踪性能明显比算法一和算法二的优。这是因为本文算法可以有效地判定粒子状态集与观测值的关联性，能很好地适应目标的机动运动状态，进而进行较准确的状态估计；算法一和算法二由于没有考虑粒子集与观测值的关联判定，当目标运动状态相近、运动模型切换或者信噪比降低时容易出现误跟踪，估计误差明显增大。当目标“新出现”或“消失”时，本文提出的算法所采用的软判定准则不能及时判定出目标数目变化，在一定程度上影响了运动状态估计精度，但是变化间隔越短，所受影响越小；而算法一和算法二的硬性判定虽然可以相对快速地检测到目标数目变化，但当受较强杂波影响时会影响目标数目的准确估计，进而导致目标状态的错误估计。

(a) 本文算法对于目标1的运动模型概率估计；(b) 算法一对于目标1的运动模型概率估计；(c) 算法二对于目标1的运动模型概率估计；(d) 本文算法对于目标2的运动模型概率估计；(e) 算法一对于目标2的运动模型概率估计；(f) 算法二对于目标2的运动模型概率估计1—CV模型；2—CT模型；3—消失状态。

(a) 本文算法对于目标1的运动模型概率估计；(b) 算法一对于目标1的运动模型概率估计；(c) 算法二对于目标1的运动模型概率估计；(d) 本文算法对于目标2的运动模型概率估计；(e) 算法一对于目标2的运动模型概率估计；(f) 算法二对于目标2的运动模型概率估计1—CV模型；2—CT模型；3—消失状态。

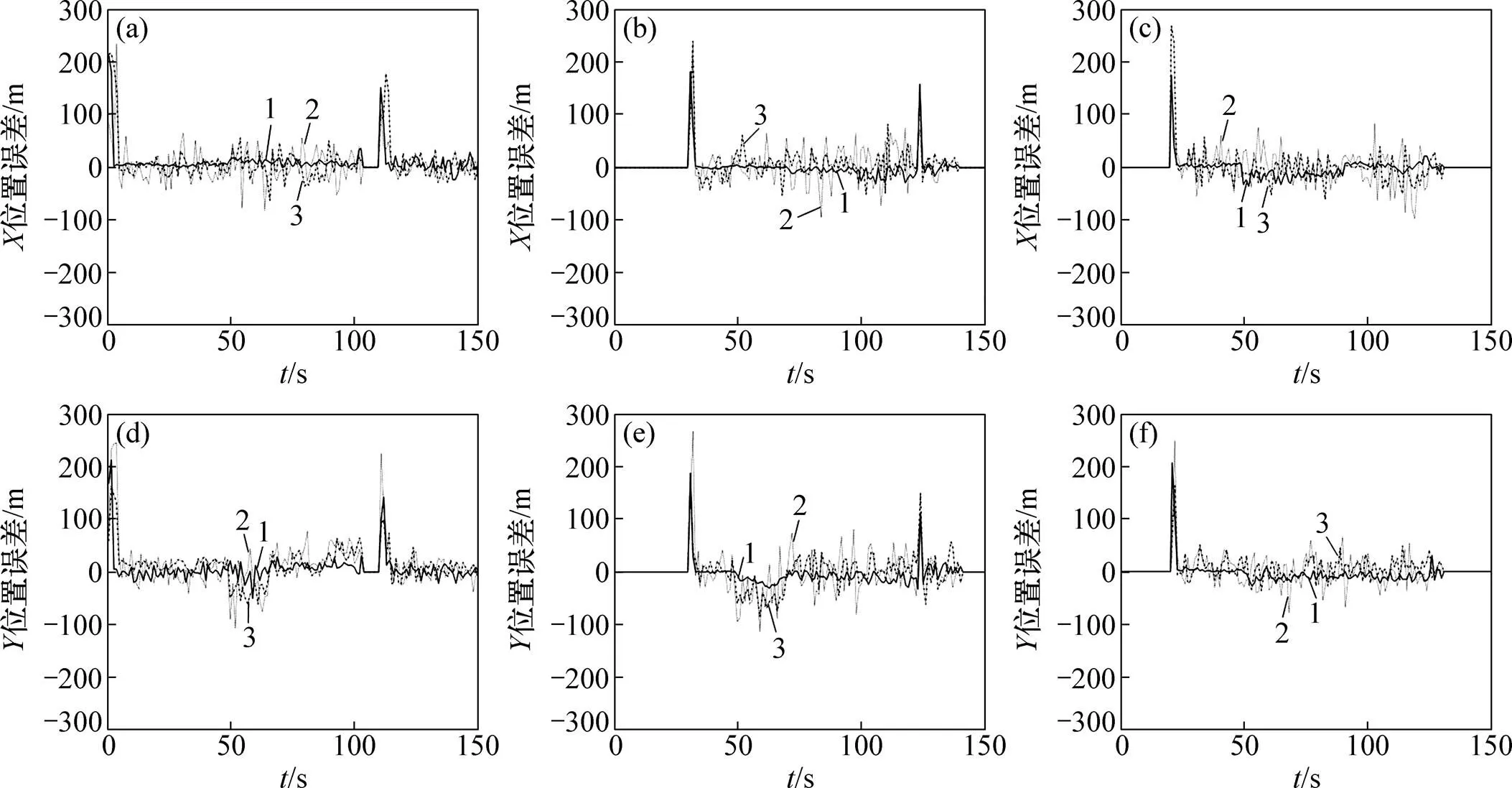
(a) 不同算法对于目标1的X方向位置状态估计；(b) 不同算法对于目标2的X方向位置状态估计；(c) 不同算法对于目标3的X方向位置状态估计；(d) 不同算法对于目标1的Y方向位置状态估计；(e) 不同算法对于目标2的Y方向位置状态估计；(f) 不同算法对于目标3的Y方向位置状态估计1—本文算法；2—算法一；3—算法二。

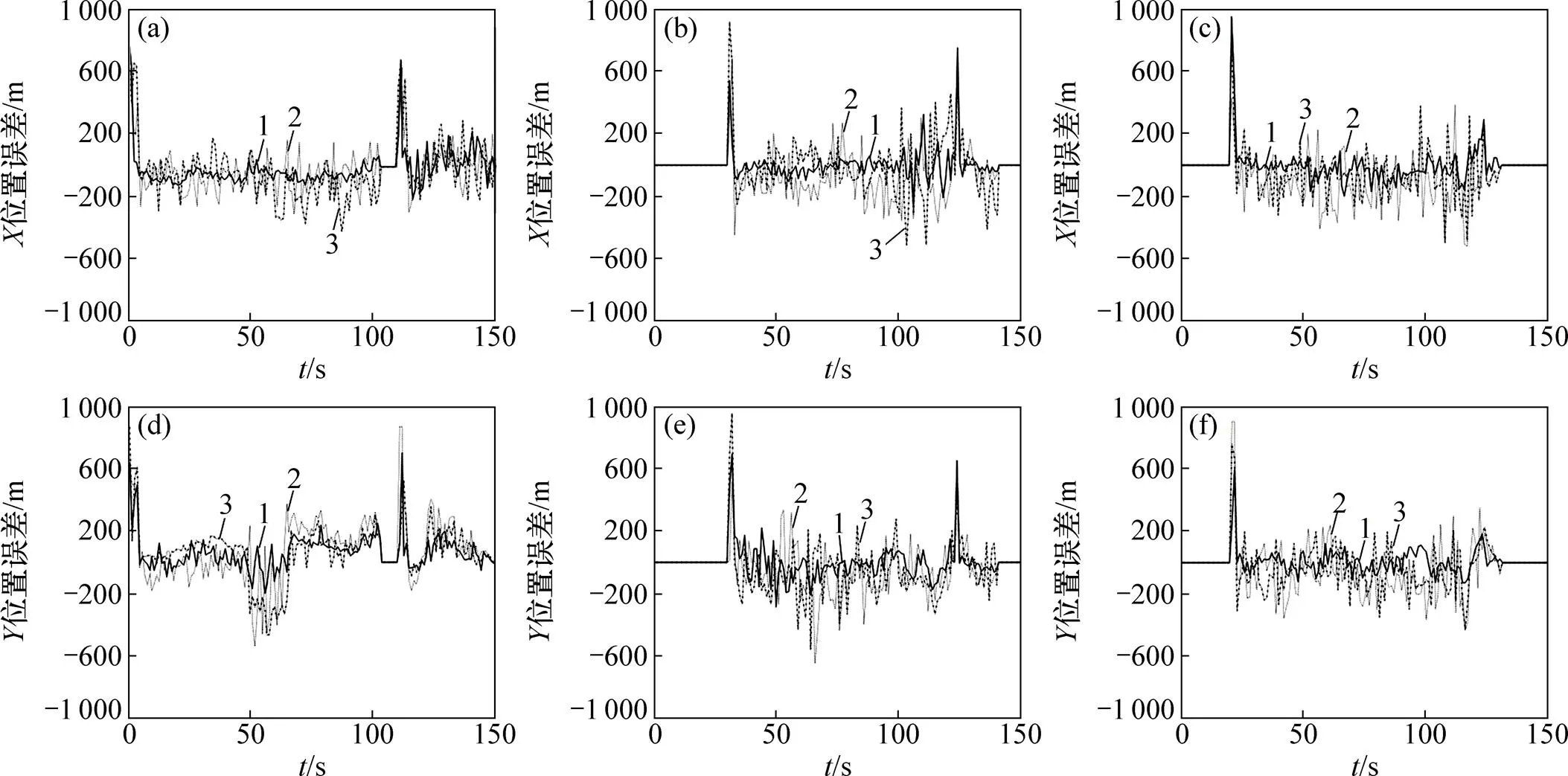
(a) 不同算法对于目标1的X方向位置状态估计；(b) 不同算法对于目标2的X方向位置状态估计；(c) 不同算法对于目标3的X方向位置状态估计；(d) 不同算法对于目标1的Y方向位置状态估计；(e) 不同算法对于目标2的Y方向位置状态估计；(f) 不同算法对于目标3的Y方向位置状态估计1—本文算法；2—算法一；3—算法二。

由图8可以看出：在相同信噪比条件下，在对目标数目的估计方面，本文算法能够较准确地估计目标数目，但是由于在判定目标出现与消失时采用了软判断准则，当目标数目发生变化时，不能即刻判定新目标出现或现有目标消失，估计出的目标数目相比于实际数目有些时间延迟；算法一由于没有考虑目标是否存在的判定，在目标数目发生变化时能及时作出判定，但是由于没有考虑目标状态与观测数据的关联性，当目标相距较近或者信噪比较低时，容易出现误跟踪及目标数目估计不准确的情况；算法二考虑了目标是否存在的判定，所采用的硬判断准则能够在一定程度上对目标数目的变化作出判定，但是受杂波影响，容易出现判定失误，并且由于没有考虑目标状态与观测数据的关联性，当目标相距较近或信噪比较低时，也容易出现误跟踪及目标数目估计不准确。对比图8(a)和8(b)可以看出：随着信噪比降低，各算法的目标数目估计准确性均有所下降，但是本文算法能更好地适应较低的信噪比环境，估计性能变化不大且明显比算法一和算法二的优。

SN/dB：(a) 8；(b) 3 1—实际数目；2—本文算法估计的目标数目；3—算法一估计的目标数目；4—算法二估计的目标数目。

图8 不同信噪比条件下各时刻不同算法估计的目标数目

Fig. 8 Estimated target number with different algorithms at each moment under different SNR conditions

从以上仿真试验及分析结果可以看出：在相同信噪比条件下，本文算法的检测与跟踪性能均比经典多模粒子滤波算法的优；随着信噪比降低，各算法的检测与跟踪性能均有所下降，但是本文算法的检测与跟踪性能仍优于经典多模粒子滤波算法。这主要是因为本文算法通过引入状态粒子集与当前观测值的模糊关联性判定，给出了目标出现与消失的软判定准则，并由混合采样得到包含模型信息和状态信息的粒子集，实现了对目标运动模型及状态变化的精确估计，有效提高了目标跟踪精度。

仿真实验中，在各算法的计算量对比上，使用单次运算所需消耗的CPU平均时间来表示，通过100次Monte Carlo仿真，给出3种算法每次迭代所需消耗的平均时间，各算法单次平均耗时的比较结果如表2所示。

表2 单次运算所需平均时间

由表2可以看出：算法一和算法二单次运算所需平均时间均比本文算法的大，本文算法的计算复杂性相对较低。这是因为本文算法增加了关联信息判定与目标数目变化的评判，但也相应地减少了无关信息的采样，算法复杂度没有明显增加。

4 结论

1) 在多模粒子滤波的框架基础上给出了一种新的目标联合检测与跟踪算法。该算法在粒子状态预测与更新步骤中，依据粒子存在变量进行预测粒子状态集的采样，考虑状态粒子集与当前观测值的模糊关联程度，给出目标出现与消失的判定准则，依据混合采样方法得到包含模型信息和状态信息的粒子集，实现了对目标运动模型及状态变化的准确估计；同时，考虑粒子存在变量影响和目标模型概率，得到各传感器各目标的融合状态估计值，优化了目标跟踪性能。

2) 在低信噪比条件下，新算法能有效处理目标相距较近或者目标数目发生变化的机动目标检测与跟踪。

参考文献：

[1] BOERS Y, DRIESSEN H, TORSTENSSON J, et al. Track-before-detect algorithm for tracking extended targets[J]. IEEE Proceedings of Radar, Sonar and Navigation, 2006, 153(4): 345−351.

[2] 胡士强, 敬忠良. 粒子滤波原理及其应用[M]. 北京: 科学出版社, 2010: 89−105. HU Shiqiang, JING Zhongliang. The theory of particle filter and its application[M]. Beijing: Science Press, 2010: 89−105.

[3] MCGINNITY S, IRWIN G W. Multiple model bootstrap filter for maneuvering target tracking[J]. IEEE Transactions on Aerospace and Electronic systems, 2000, 36(3): 1006−1012.

[4] BOERS Y, DRIESSEN J N. Interacting multiple model particle filter[J]. IEEE Proceedings of Radar, Sonar and Navigation, 2003, 150(5): 344−349.

[5] DAVEY S J, GORDON N J, SABORDO M. Multi-sensor track-before-detect for complementary sensors[J]. Digital Signal Processing, 2011, 21(5): 600−607.

[6] 王晓, 韩崇昭. 基于混合采样的多模型机动目标跟踪算法[J]. 自动化学报, 2013, 39(7): 1152−1156. WANG Xiao, HAN Chongzhao. A multiple model particle filter for maneuvering target tracking based on composite sampling[J]. Acta Automatica Sinica, 2013, 39(7): 1152−1156.

[7] 吴瑕, 陈建文, 鲍拯, 等混合估计多模粒子滤波的机动弱目标检测前跟踪算法[J]. 控制与决策, 2014, 29(3): 523−527. WU Xia, CHEN Jianwen, BAO Zheng, et al. Track-before-detect for maneuvering weak target based on mixture estimation of multi model particle filter algorithm[J]. Control and Decision, 2014, 29(3): 523−527.

[8] WANG Guohong, TAN Shuncheng, GUAN Chengbin, et al. Multiple model particle filter track-before-detect for range ambiguous radar[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1477−1487.

[9] 鉴福升, 徐跃民, 阴泽杰. 改进的多模型粒子滤波机动目标跟踪算法[J]. 控制理论与应用, 2011, 27(8): 1012−1016. JIAN Fusheng, XU Yuemin, YIN Zejie. Enhanced multiple model particle filter for maneuvering target tracking[J]. Control Theory and Applications, 2011, 27(8): 1012−1016.

[10] YANG T, BLOM H A P, MEHTA P G. Interacting multiple model-feedback particle filter for stochastic hybrid systems[C]//2013 IEEE 52nd Annual Conference on Decision and Control (CDC). Florence: IEEE, 2013: 7065−7070.

[11] HUANG Dayu, XUE Anke, GUO Yunfei. A Particle filter track-before-detect algorithm for multi-radar system[J]. Electronics and Electrical Engineering, 2013, 19(5): 3−8.

[12] ZHANG G, YANG C, ZHANG Y. A Track-before-detect method based on particle filters for target detection[J]. Journal of Computational Information Systems, 2013, 9(18): 7281−7289.

[13] ZAVLANOS M M, SPESIVTSEV L, PAPPAS G J. A distributed auction algorithm for the assignment problem[C]//2008 IEEE 47th Conference on Decision and Control (CDC). Cancun: IEEE, 2008: 1212−1217.

[14] POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33−57.

[15] BOERS Y, DRIESSEN J N. Interacting multiple model particle filter[J]. IEEE Proceedings: Radar, Sonar and Navigation, 2003, 150(5): 344−349.

[16] 龚亚信, 杨宏文, 胡卫东, 等. 基于多模粒子滤波的机动弱目标检测前跟踪[J]. 电子与信息学报, 2008, 30(4): 941−944. GONG Yaxin, YANG Hongwen, HU Weidong, et al. Multiple model particle filter based track-before-detect for maneuvering weak target[J]. Journal of Electronics and Information Technology, 2008, 30(4): 941−944.

[17] ZHAI Y, YEARY M B, CHENG S, et al. An object-tracking algorithm based on multiple-model particle filtering with state partitioning[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(5): 1797−1809.

(编辑 赵俊)

New method for joint detection and tracking with variable maneuvering target number

HU Xiuhua, GUO Lei, LI Huihui, YAN Pandeng

(College of Automation, Northwestern Polytechnical University, Xi’an 710129, China)

Aiming at the problem of low target tracking performance with the variable number of maneuvering target, a new joint detection and tracking algorithm was put forward for the environment of low signal-to-noise ratio multi-sensor observation. The sampling of predict state particle set was completed according to the existence of the particle. And then, taking the association degree of the sets of particle state and the current observations into account, and using the theory of fuzzy auction algorithm and particle swarm optimization, the association problem between the state and observation sets was solved, and the criteria of target appear and disappear was given, and the updating of particle weight was realized. By the means of composite sampling, the sample particle sets with the model information and status information was obtained, and the local posteriori estimate and the mean square error of target state were given with the target model probability through particle state fusion. Finally, with the weighted fusion of each associated local sensor tracking information, the global state estimation of each target was obtained and compared with the simulation experiment with classical multiple model particle filter algorithm. The results show that the new algorithm is effective in motion model probability estimation, state estimation, and the target number estimation.

multi-model particle filter; detection and tracking; associated determination; target; composite sampling

10.11817/j.issn.1672-7207.2016.10.020

TP391

A

1672−7207(2016)10−3424−12

2015−10−03；

2016−01−17

国家自然科学基金资助项目(60802084)；武器装备预先研究基金资助项目(51306030205) (Project(60802084) supported by the National Natural Science Foundation of China; Project(51306030205) supported by the Weapons and Equipment Research Funds in Advance)

胡秀华，博士研究生，从事多传感器目标融合检测、跟踪与识别研究；E-mail：huxhnwpu2010@163.com