GEOMETRIC TRANSIENCE FOR NON-LINEAR AUTOREGRESSIVE MODELS

SONG Yan-hong

(School of Statistics and Mathematics，Zhongnan University of Economics and Law，Wuhan 430073，China）

GEOMETRIC TRANSIENCE FOR NON-LINEAR AUTOREGRESSIVE MODELS

SONG Yan-hong

(School of Statistics and Mathematics，Zhongnan University of Economics and Law，Wuhan 430073，China）

In the paper，we study the stochastic stability for non-linear autoregressive models.By establishing an appropriate Foster-Lyapunov criterion，a sufficient condition for geometric transience is presented.

geometric transience；non-linear autoregressive model；Foster-Lyapunov criterion

2010 MR Subject Classification：60J05；60J20；37B25

Document code：AArticle ID：0255-7797（2016）05-0987-06

1 Introduction

Consider a non-linear autoregressive Markov chainondefined by

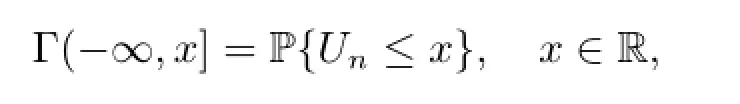
First，let us recall some notations and definitions，see［3，5，6］for details.Denote by）the Borel σ-field on R，and write=.The n-steptransition kernel of the chain Φnis defined as

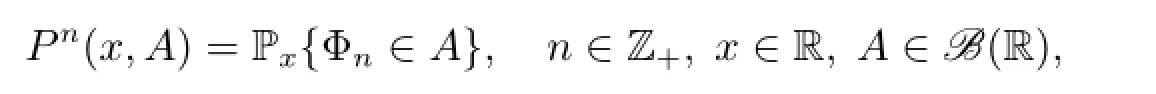
The chain Φnis Lebesgue-irreducible，if for every

Obviously，the subset of a petite set is still petite.By［7，Lemma 2.1］or［8，Theorem 1］，we know that the non-linear autoregressive model is Lebesgue-irreducible，and every compact set inis petite.

be the first return and first hitting times，respectively，on A.It is obvious that τA=σAif Φ0∈Ac.Denote by L（x，A）=the probability of the chain Φnever returning to A.

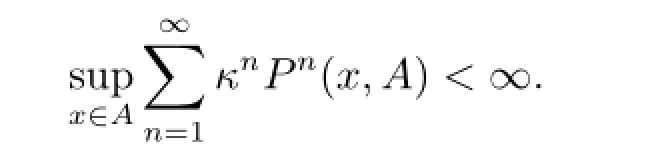
The chain Φnis called geometrically transient，if it is ψ-irreducible for some non-trivial measure ψ，and R can be covered ψ-a.e.by a countable number of uniformly geometrically transient sets.That is，there exist sets D and Ai，i=1，2，···such that=D∪where ψ（D）=0 and each Aiis a uniformly geometrically transient set of the chain Φn.

To state the main result of this paper，we need the following assumptions：

Theorem 1.1Assume（A1）and（A2）.Then the non-linear autoregressive model Φnis geometrically transient.

Remark 1.2It is easy to see that（A2）is equivalent to the condition in［9，Theorem 3.1］，where transience for the the non-linear autoregressive model Φnwas confirmed.Here，we get a stronger result（i.e.geometric transience）in Theorem 1.1.

2 Proof of Theorem 1.1

This section is devoted to proving Theorem 1.1 by using the Foster-Lyapunov（or drift）condition for geometric transience.

It is well known that Foster-Lyapunov conditions were widely used to study the stochastic stability for Markov chains.For examples，Down，Meyn and Tweedie［10-13］studied the drift conditions for recurrence，ergodicity，geometric ergodicity and uniform ergodicity.The drift conditions for sub-geometric ergodicity were discussed in［1，4，14-17］and so on.In ［18，19］，the drift conditions for transience were obtained.

Recently，we investigated the drift condition for geometric transience in［6］.One of the main results shows that the chain Φnis geometrically transient，if there exist some set，constants λ，b∈（0，1），and a function W≥1A（with W（x0）＜∞for somesatisfying the drift condition

As far as we know，however，this drift condition can not be applied directly for the nonlinear autoregressive model considered in this paper.Alternatively，we will establish a more practical drift condition for geometric transience.First，we need the following two lemmas，which are taken from［6］.

Lemma 2.1The chain Φnis geometrically transient if and only if there exist someand a constant κ＞1 such that

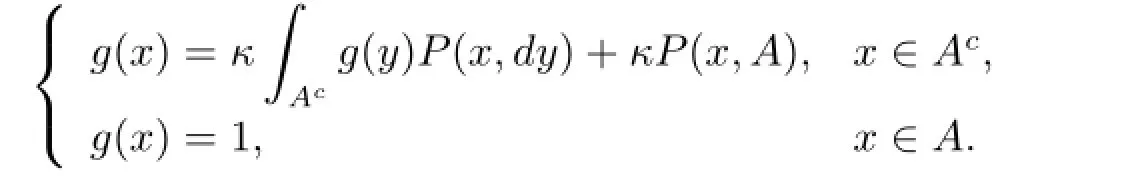
Proposition 2.3The chain Φnis geometrically transient，if there exist a petite set，constants λ∈（0，1），b∈（0，∞），and a non-negative measurable function W bounded on A satisfying

and

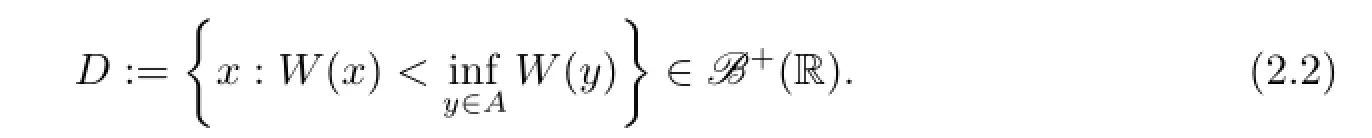
ProofSince W is non-negative and），we have.Set

Hence by the comparison theorem of the minimal non-negative solution（see［20，Theorem 2.6］），we know from（2.3）and（2.4）that

By（2.5）and noting that D⊂Ac，we have for all x∈R，

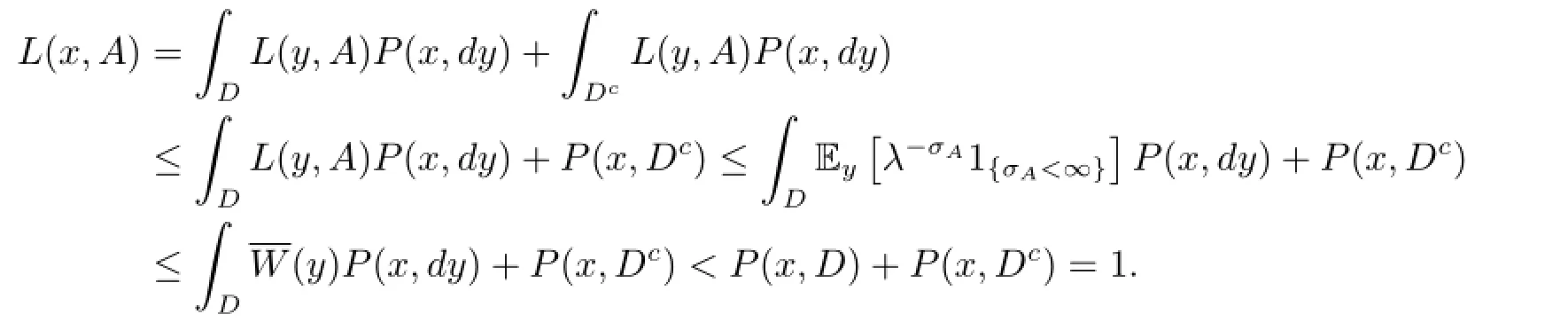
Thus there exists some set C⊂A withsuch that

According to Lemma 2.1，in the following，it is enough to prove that for some κ＞1，

Combining Lemma 2.2（1）with（2.5）and（2.1），we get for all x∈A，

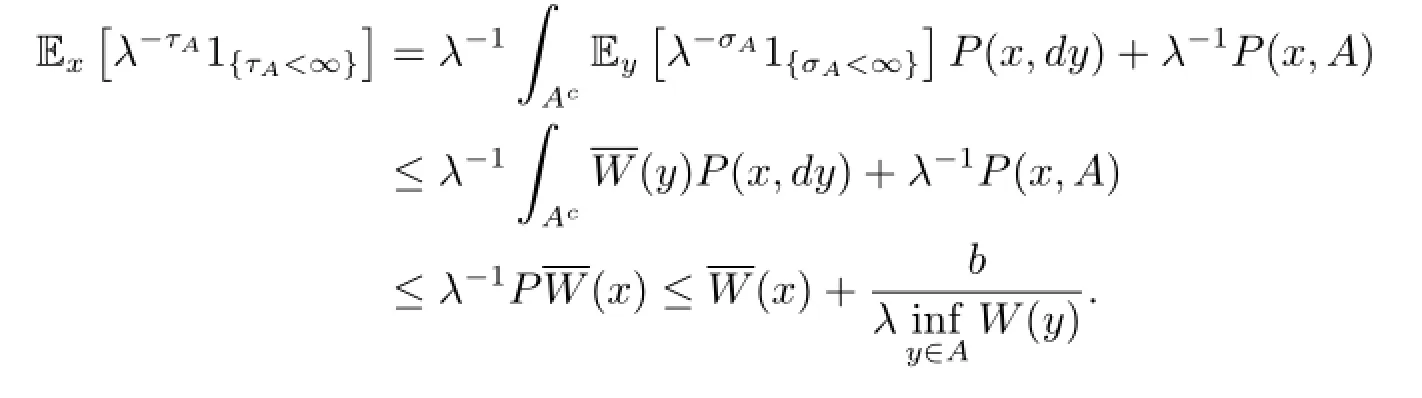
Since W is bounded on A，

Noting that A is petite and C⊂A，according to（2.7）and the proof of［3，Theorem 15.2.1］，we obtain that for all 1＜κ≤λ-1/2＜∞.This together with（2.6） yields the desired assertion.

Now，we are ready to prove Theorem 1.1.

Proof of Theorem 1.1By（A2），there exist constants θ＞0 and c＞0 satisfying

Choose

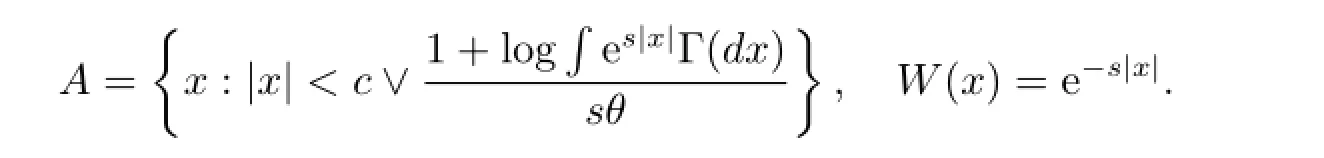
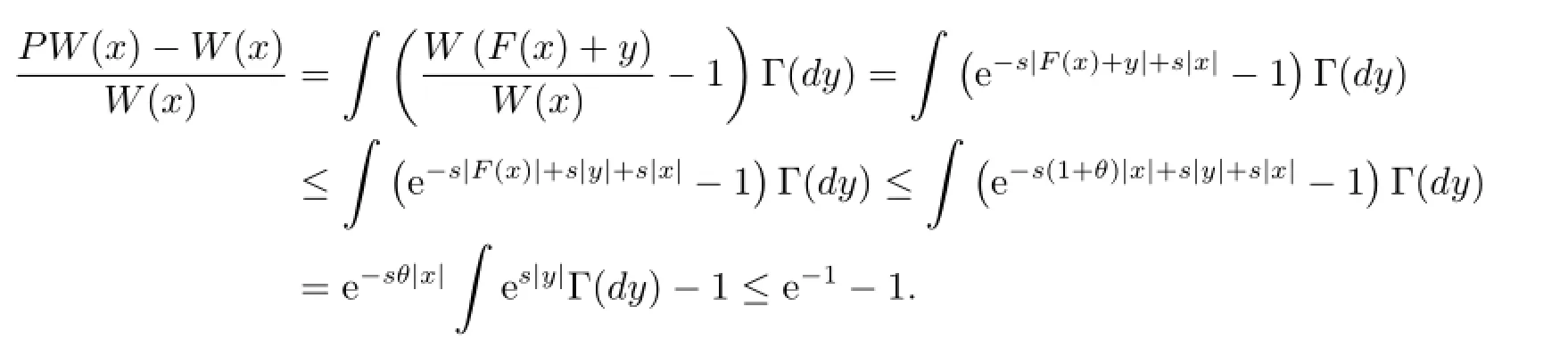
That is，

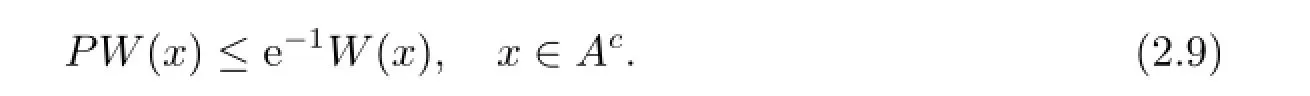
Noting that W is bounded，it is obvious that for some b∈（0，∞），

Combining this with（2.9），the drift condition（2.1）holds.Thus the non-negative autoregressive model Φnis geometrically transient by Proposition 2.3.

References

［1］Douc R，Fort G，Moulines E，Soulier P.Practical drift conditions for subgeometric rates of convergence［J］.Ann.Appl.Prob.，2004，14（3）：1353-1377.

［2］Fort G，Moulines E.Polynomial ergodicity of Markov transition kernels［J］.Stoch.Proc.Appl.，2003，103（1）：57-99.

［3］Meyn S P，Tweedie R L.Markov chains and stochastic stability（2nd ed.）［M］.London：Springer-Verlag，1993.

［4］Tuominen P，Tweedie R L.Subgeometric rates of convergence of f-ergodic Markov chains［J］.Adv. Appl.Prob.，1994，26（3）：775-798.

［5］Gao Zhenlong，Wang Weigang，Hu Dihe.The convergence for transition functions of Markov chains in random environments［J］.J.Math.，2008，28（5）：546-550.

［6］Mao Yonghua，Song Yanhong.On geometric and algebraic transience for discrete-time Markov chians［J］.Stoch.Proc.Appl.，2014，124（4）：1648-1678.

［7］An H Z，Huang F C.The geometrical ergodicity of nonlinear autoregressive models［J］.Stat.Sinica，1996，6：943-956.

［8］Bhattacharya R，Lee C.On geometric ergodicity of nonlinear autoregressive models［J］.Stat.Prob. Lett.，1995，22（4）：311-315.

［9］Lee O.Geometric ergodicity and transience for nonlinear autoregressive models［J］.Comm.Korean Math.Soc.，1995，10（2）：409-417.

［10］Down D，Meyn S P，Tweedie R L.Exponential and uniform ergodicity of Markov processes［J］.Ann. Prob.，1995，23（4）：1671-1691.

［11］Meyn S P，Tweedie R L.Stability of Markovian processes I：criteria for discrete-time chains［J］.Adv. Appl.Prob.，1992，24（3）：542-574.

［12］Meyn S P，Tweedie R L.Stability of Markovian processes II：continuous time processes and sampled chains［J］.Adv.Appl.Prob.，1993，25（3）：487-517.

［13］Meyn S P，Tweedie R L.Stability of Markovian processes III：Foster-Lyapunov criteria for continuous time processes［J］.Adv.Appl.Prob.，1993，25（3）：518-548.

［14］Jarner S F，Roberts G O.Polynomial convergence rates of Markov chains［J］.Ann.Appl.Prob.，2002，12（1）：224-247.

［15］Mao Yonghua.Algebraic convergence for discrete-time ergodic Markov chains［J］.Sci.China Ser.A，2003，46（5）：621-630.

［16］Mao Yonghua.Ergodic degrees for continuous-time Markov chains［J］.Sci.China Ser.A，2004，47（2）：161-174.

［17］Fort G，Roberts G O.Subgeometric ergodicity of strong Markov processes［J］.Ann.Appl.Prob.，2005，15（2）：1565-1589.

［18］Stramer O，Tweedie R L.Stability and instability of continuous time Markov processes［C］.Chichester：Wiley，Prob.，Stat.Optim.，1994：173-184.

［19］Tweedie R L.Criteria for classifying general Markov chians［J］.Adv.Appl.Prob.，1976，8（4）：737-771.

［20］Chen Mufa.From Markov chains to non-equilibrium particle systems（2nd ed.）［M］.Singapore：Word Sci.，2004.

非线性自回归模型的几何非常返性

宋延红
（中南财经政法大学统计与数学学院，湖北武汉430073）

本文研究了非线性自回归模型的随机稳定性.通过建立恰当的Foster-Lyapunov条件，得到了非线性自回归模型几何非常返的充分条件.

几何非常返；非线性自回归模型；Foster-Lyapunov条件

MR（2010）主题分类号：60J05；60J20；37B25O211.62；O211.9

date：2016-03-11Accepted date：2016-06-01

Supported by National Natural Science Foundation of China（11426219；11501576）.

Biography：Song Yanhong（1983-），female，born at Yantai，Shandong，lecturer，major in probability.