基于马尔科夫模型的认知无线电动态双门限能量检测策略

刘玉磊 梁 俊 肖 楠 扈瑜龙 胡 猛



基于马尔科夫模型的认知无线电动态双门限能量检测策略

刘玉磊*梁 俊 肖 楠 扈瑜龙 胡 猛

(空军工程大学信息与导航学院 西安 710077)

该文针对低信噪比条件下频谱感知精度低的问题，提出一种基于马尔科夫模型的动态双门限能量检测算法。该算法根据信道时变特性建立基于马尔科夫的频谱占用模型，利用信道历史状态信息实现模型参数的修正。然后采用“先听后说”的机制对处于双门限之间的“困惑”信道状态进行判决，并详细分析了噪声不确定性对频谱感知性能的影响。在此基础上，为了克服噪声不确定性的影响，以频谱检测概率最大为优化目标，对双门限进行实时更新。仿真结果表明，所提频谱感知算法在减小噪声不确定性影响的同时增加了频谱感知精度，降低了认知用户的感知时间。

频谱感知；能量检测；马尔科夫模型；动态双门限

1 引言

随着无线通信系统用户数量极具增加，使得在现有的静态频谱管理框架下，可用的频谱资源日益稀缺。根据国际电信联盟的研究报告，在特定时间和地理位置已分配的频谱存在利用率低下的现象[1]。认知无线电技术可以有效解决频谱短缺问题。在认知无线电通信系统中，认知用户(SUs)通过频谱感知发现主用户(PUs)未被占用的空闲信道并利用其进行通信。因此，作为认知无线电中的一项关键技术，频谱感知在促进认知无线电实现中发挥着重要作用，并且成为近年来研究的焦点。

频谱感知方法主要包括：主流的方法，如能量检测、相干检测、循环平稳特征检测、自相关检测、无线射频识别等；其他方法，包括多窗谱估计、小波变换、霍夫变换、时频分析等。其中，能量检测是最常用的方法，因为它计算简单，不需要待检测信号的先验知识，硬件实现比较容易。然而，传统能量检测算法在低信噪比条件下检测性能急剧下降。与传统能量检测使用单一阈值不同，一些近期研究采用双阈值判决机制。文献[6]介绍了一种基于双阶段的协作频谱感知策略，在第1阶段采用单门限能量检测，在后一阶段采用双门限能量检测，通过中心对各合作认知节点的感知结果进行融合判决，但并未对融合判决规则进行详细分析说明。文献[7]提出了一种通过两步频谱感知来提高检测性能的方案，该方案首先进行双门限能量检测，然后对处在两门限间的频谱状态采用循环平稳特征检测来判决，但这种方案计算复杂度较高，需要更多的感知时间。文献[8]采用双门限能量检测进行频谱感知，将局部能量检测结果分为硬判决和软判决。但是最终的判决结果是由融合中心给出，实现起来较为复杂。文献[9]通过在表决融合准则中优化表决参数以实现认知无线电网络的吞吐量最大化的目标，但是由于其双门限是固定的，使得该方法在复杂的电磁环境下检测性能降低。文献[10]通过增加样本数量实现对处于两门限之间的频谱状态判决，但是有时为了得到判决结果会导致样本数量急剧增加，从而导致算法的实时性降低。

然而上述方法均未对双门限的确定进行深入研究。尽管其中一些方法通过引入噪声不确定性来计算双门限，但在现实环境中，噪声的不确定性仍是未知的。其次，大多数的双门限能量检测方法基于合作环境或与其他检测方法结合，这将增加计算的复杂度以及感知时间。最后，大多数文献并没有关于检测时间的分析。

综上，本文提出了一种适用于认知无线电的动态双门限能量检测算法。通过带约束条件的最优函数实现双门限的动态调整。此外，还建立了马尔科夫频谱占用模型来统计信道状态，并利用信道的历史状态信息对模型参数进行修正。若接收到的信号能量大于上限阈值，则信道被判决为占用；若检测统计量低于下限阈值，则该信道被判决为空闲，可被认知用户使用；如果收集的能量值介于两个阈值间，则通过对以前信道状态的统计结果进行信道状态判决。

2 能量检测算法

一个较宽的频带可以被划分为同样大小的个子信道，对于某个子信道，其对应的频率为f。基于认知用户接收到的信号来检测主用户的存在与否。这是一个典型的二元假设问题。信道上接收到的次采样信号可以通过式(1)的假设表示为[11,12]

2.1 传统能量检测算法

在传统的能量检测算法中，认知用户通过对其接收到的信号与先验门限进行比较来做出判决。0或的判决取决于子信道主用户的信号能量是否高于或低于门限值。检验统计量为[13]

其中，为样本数量，表示接收到的信号能量。当样本数量足够大时，子信道的检验统计量可以近似为正态变量。因此，在0与1条件下服从正态分布：

2.2双门限能量检测算法

一般情况下，假设接收端的噪声功率是确定的。然而，在现实环境中，噪声不仅包括高斯白噪声，还包括其他一些干扰，并且噪声功率在一定范围内随着时间的推移和发收双方相对位置的变化而改变。这种噪声不稳定的情况称之为噪声不确定性。这会引起检测性能变差(检测概率降低并且虚警概率增加)，尤其是当噪声不确定性增加时。为了使检测结果更加可靠，减少噪声不确定性的影响，双门限能量检测方法应运而生。假设无线信道的噪声不确定性被描述为[15]

通常情况下：对于某个特定的子信道状态可以通过两个随机变量进行建模，分别为“频带占用”(信号存在)与“频带空闲”(信号不存在)。然而，有时候子信道状态存在模糊的情况，不能单纯的通过二元假设检验进行判决，这种情况下就会被归类为“困惑”状态。子信道检测统计量通过与两个门限值进行比较被判决为主用户信号(由“1”表示)，噪声(由“0”表示)亦或是困惑状态(由“”表示)，如式(8)所示。

图1 噪声与主用户信号的能量分布

困惑状态可以借助于额外的信息或者与网络中其他无线认知用户协作进行判决[16]。本文利用“先听后说”的机制来判决信道的困惑状态。在这种方法中，“困惑”的信道状态的解决借助于以前观察到的信道状态。图2给出了困惑信道状态的判决过程。这一判决也可以基于在指定的一段观察时间内信道状态，而不是之前某一时刻的信道状态。

图2 信道状态判决过程

当当前信道状态是“困惑”时，则当前信道状态通过前一时刻的信道状态进行判决：若前一时刻信道状态是“频带占用”，那么当前信道状态是“占用”；否则，当前信道状态是“频带空闲”。

3 频谱占用的马尔科夫模型

由图3所示，子信道的频谱占用状态可以通过两状态的马尔科夫链描述。用0和1分别表示状态0和1的概率，状态转换概率为00,01,10,11。在之前的研究中[17]，信道占用马尔可夫模型的建立的前提是假定信道状态是静止的。然而，在实际中，模型参数会随着时间变化。例如，移动单元信道的使用峰值出现在每天的工作时间。为了计算模型中的各参数，必须制定一种权值计算方法，使得当前瞬时信道状态获得更大权值。

图3 信道马尔科夫模型

为了捕获时变信道频谱占用模型的动态特征，这里提出一种权重计算方法，保证当前瞬时信道状态拥有较大权值。子信道在时刻，通过对过去检测信道状态为1的次数进行统计，相应的状态概率定义为

其他模型参数也可通过该方法计算得到。

在获取模型参数样本分布之前，这里做一个合理的假设：信道频谱占用是分段平稳的。例如，一周的正常工作日的非高峰时段，移动单元的信道频谱占用是接近稳定的。因此，本文的研究基于分段时间间隔内信道频谱占用状态稳定性的基础之上。

由式(13)可知，对于给定的置信区间，估计的精度随着样本数量的增大而增高。

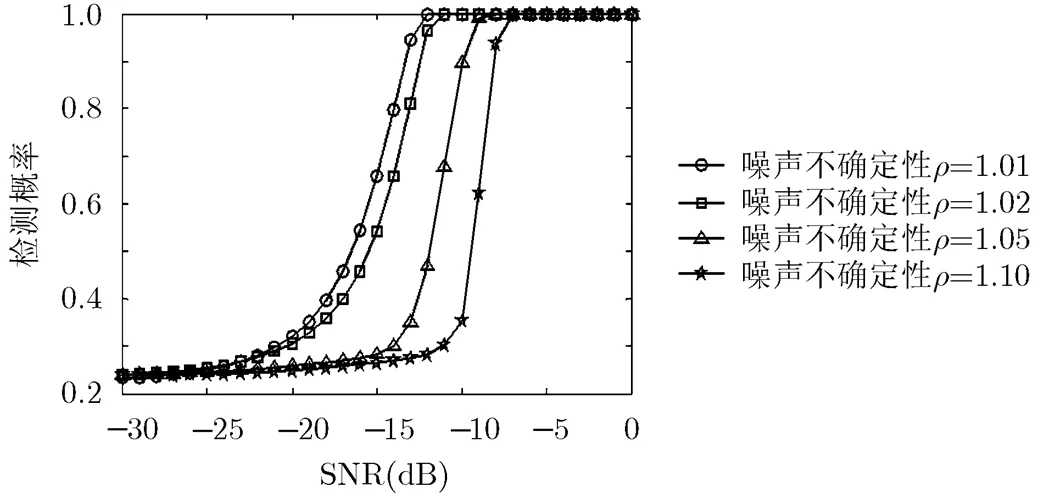
图4 不同噪声不确定性下的DEMM的性能比较

4 自适应双门限能量检测算法

基于双门限检测算法和马尔科夫频谱占用模型，这里提出了一种动态双门限能量检测算法。若为虚警概率，为检测概率，则

那么

根据Neyman-Pearson准则[20]，给定虚警概率，目的为了得到最优的双门限和，使得检测概率最大。该问题可以被描述为

那么，式(18)可以被重写为

这里给出详细的推导过程。将式(4)和式(19)代入式(17)可以得到与的详细表达式。

5 仿真结果与分析

在这部分，提供仿真结果来验证所提出DDEMM频谱感知算法的优势。以下所有图中，“Two-stage-DE”为文献[6]提出的两阶段双门限能量检测算法，“Cyclostation-DE”表示文献[7]提出的基基于循环平稳特征的双门限能量检测算法，“CSBDE”为文献[8]提出的基于双门限能量检测的协作频谱感知算法，“VRODE”为文献[9]提出的优化表决融合准则下的双门限协作能量检测算法，“ADE”为文献[10]提出的自适应双门限能量检测算法，“DDEMM”表示本文提出的基于马尔科夫模型的动态双门限能量检测算法。

仿真条件如下：主用户信号为QPSK调制，信道频率混合后接收端的信号形式为,为功率的标准高斯白噪声，采样频率为，置信水平为，虚警概率，对比的协作感知算法采用两个感知节点(N=2)。设定具有噪声不确定性的白噪声。

图5给出了不同噪声不确定度下DDEMM算法的性能比较。可以看出若噪声不确定性0，当信噪比高于-10 dB时，检测性能几乎不受噪声不确定性的影响；在信噪比低于-10 dB时，随着信噪比的降低，检测性能随着噪声不确定性的增加而变差。在信噪比为-15 dB时，噪声不确定性增加8.91%，检测性能下降2.73%。但随着噪声不确定的性的增加，尤其是当0，噪声不确定性对算法的性能影响较大，尽管DDEMM仍然受噪声不确定性的影响，但是与图4相比，DDEMM频谱感知方法较DEMM方法降低了对噪声不确定度的敏感程度，初步具有对噪声不确定度的鲁棒性。这是由于DDEMM算法中的双门限的确定是基于最大检测概率。根据前面几节的讨论分析可知，最优双门限可以使得大部分统计检验量在噪声不确定的条件下处于困惑区域之外。

图5 不同噪声不确定度下的性能比较

图6 各算法检测性能对比

频谱感知时间也就是感知算法的时效性是衡量感知性能的重要指标之一，若感知的时间较长，虽然可以在一定程度上提高感知精度，但是会降低次用户的传输时间，从而降低网络吞吐量。在虚警概率，噪声不确定性的条件下，图7给出了不同信噪比下频谱感知时间。本文所提出的DDEMM算法较之前所提出的几种算法所需的感知时间较少。并且频谱感知时间与信噪比有一定关系：随着信噪比的增加，频谱感知时间减小。在信噪比为-20 dB时，DDEMM所需感知时间约为46.7 ms，而以前的算法(CSBDE(N=2), Cyclostation-DE，“Two-stage”-DE, VORDE(N=2)和ADE大约需要61.2 ms, 53.4 ms, 48.9 ms, 55.1 ms和80.8 ms。结果表明DDEMM比其他5种算法相比在满足感知精度的前提下可以在一定程度上降低频谱感知时间。图8给出了满足检测概率时所需的最少样本数量。在信噪比为-10 dB和-15 dB时，在达到相同的检测精度的条件下，DDEMM需要的样本数量最少，CSBDE和Cyclostationary-DE次之，“Two-stage”-DE需要的样本数量最多。在信噪比为-20 dB和-25 dB时，在达到相同的检测精度的条件下，Cyclostationary-DE和ADE算法所需要的样本数量最多，CSBDE，“Two-stage”-DE 和VORDE (N=2)算法所需要的样本数量次之，DDEMM需要的样本数量最少。并且在信噪比为-20 dB时，Cyclostationary-DE算法已经无法满足所要求的检测性能。

图7 频谱感知时间(Pf=0.1, N=1000)

图8 所需的样本数量(Pf=0.1, Pd≥0.9)

6 结论

本文提出了基于马尔科夫模型的双门限能量检测算法，通过优化函数来动态的确定双门限。修正的马尔科夫模型的建立，使用算法能够对困惑状态做出相应决策。分析了噪声不确定度对双门限能量检测性能的影响。并且以检测概率最大化为目标来动态的确定最优双门限，使得该算法降低了对噪声不确定度的影响。仿真结果显示该算法与之前的方法相比感知性能显著提高。

参考文献

[1] MCHENRY M A. RED: NSF spectrum occupancy measurements project summary[OL]. http://www. sharedspectrum.com, 2005.

[2] YUE W J, ZHENG B Y, MENG Q M,. Robust cooperative spectrum sensing schemes for fading channels in cognitive radios networks[J]., 2011, 41(2): 207-218. doi: 10.1007/s11432-010-4147-x.

[3] LOREDANA A and DANIELE T. Statistical modeling of spectrum sensing energy in multi-hop cognitive radio networks[J]., 2015, 22(3): 356-360. doi: 10.1109/LSP.2014.2360234.

[4] YÜCEK and ARSLAN H. A survey of spectrum sensing algorithms for cognitive radio applications[J].&, 2009, 11(1): 116-130. doi: 10.1109/SURV.2009.090109.

[5] GILBERT S, KUHN F, NEWPORT C,. Efficient communication in cognitive radio networks[C]. Proceedings of ACM SPDC. California, USA, 2015: 119-128. doi: 10.1145 /2767386.2767422.

[6] BAGWARI A, TOMAR G S, and VERMA S. Cooperative spectrum sensing based on two-stage detectors with multiple energy detectors and adaptive double threshold in cognitive radio networks[J]., 2013, 36(4): 172-180. doi: 10.1109/ CJECE.2014.2303519.

[7] MALEKI S, PANDHARIPANDE A, and LEUS G. Two-stage spectrum sensing for cognitive radios[C]. Proceedings of IEEE ICASSP. New York, USA, 2010: 2946-2949. doi: 10.1109/ICASSP.2010.5496149.

[8] CHEN C X, FU H, NIU Z D,Cooperative spectrum sensing algorithm based on double-threshlod energy detection[J]., 2013, 35(8): 1742-1746. doi: 10.3969/j.issn.1001-506X.2013.08.26.

[9] HORGAN D and MURPHY C. Voting rule optimisation for double threshold energy detector-based cognitive radio networks[C]. Proceedings of IEEE 4th International Conference on Signal Processing and Communicating Systems, Australia, 2010: 1-8. doi: 10.1109/ICSPCS.2010.- 5709679.

[10] FANG L, WANG J K, and HAN Y H. An adaptive double thresholds scheme for spectrum sensing in cognitive radio networks[J]., 2013, 63(1): 47-52. doi: 10.1109/ICSPCC.2013.6664104.

[11] HERATH S, RAJATHEVA N, and TELLAMBURA C. Energy detection of unknown signals in fading and diversity reception[J]., 2011, 59(9): 2443-2453. doi: 10.1109/TCOMM.2011.071111.090349.

[12] SUN H J and NALLANATHAN A. Wideband spectrum sensing for cognitive radio networks: a survey[J]., 2013, 20(2): 74-81. doi: 10.1109/ MWC.2013.6507397.

[13] CABRIC D, TKACHENKO A, and BRODERSEN R W. Experimental study of spectrum sensing based on energy detection and network cooperation[C]. Proceedings of the First International Workshop on Technology and Policy for Accessing Spectrum. New York, USA, 2006: 12. doi: 10.1145/1234388.1234400.

[14] LI Z X, WANG H, and KONG J. A two-step spectrum sensing scheme for cognitive radio network[C]. Proceeding of the International Conference on Information Science and Technology. Nanjing, China, 2011: 694-698. doi: 10.1109/ ICIST.2011.5765341.

[15] ZENG Y and LIANG Y C. Spectrum sensing algorithms for cognitive radio based on statistical covariances[J]., 2009, 58(4): 1804-1815. doi: 10.1109/TVT.2008.2005267.

[16] CHEN W B, YANG C K, and HUANG Y H. Energy-saving cooperative spectrum sensing processor for cognitive radio systems[J]., 2011, 58(4): 711-723. doi: 10.1109/TCSI.2010.2078691.

[17] ATAPATTU S, TELLAMBURA C, HAI J,. Unified analysis of low-SNR energy detection and threshold selection[J]., 2015, 64(11): 5006-5019. doi: 10.1109/TVT.2014.2381648.

[18] 谢显中, 胡小峰, 马彬. 噪声功率不确定性区间估计和降低SNA WALL恶化的能量检测算法[J]. 电子与信息学报, 2014, 36(2): 364-370. doi: 10.3724/SP.J.1146.2013.00928.

XIE X Z, HU X F, and MA B. Estimation of noise power uncertainty interval and energy detector with lowering SNR WALL detection[J].&, 2014, 36(2): 364-370. doi: 10.3724/SP.J.1146. 2013.00928.

[19] SHEN B, WANG S, and HUANG Q. Gerschgorin disk theorem based spectrum sensing for wideband cognitive radio[J]., 2014, 35(4): 1-10. doi: 10.1109/ICASSP.2014.6855013.

[20] ATAOLLAH E, MARYAM N, SEYED M H A,. Sensor selection and optimal energy detection threshold for efficient cooperative spectrum sensing[J]., 2015, 64(4): 1565-1577. doi: 10.1109/ TVT.2014.2331681.

Dynamic Double Threshold Energy Detection Based on Markov Model in Cognitive Radio

LIU Yulei LIANG Jun XIAO Nan HU Yulong HU Meng

(,,’710077,)

With the development of the technology of cognitive radio, the standards of spectrum sensing performance become the higher and the higher, especially in low Signal-to-Noise Ratio (SNR) environments. A Dynamic Double-threshold Energy sensing method based on Markov Model (DDEMM) is proposed in this paper. By following the double-threshold energy sensing approach, the modified Markov model that accounts for the time varying nature of the channel occupancy is presented to resolve the ‘confused’ channel state. Furthermore, in order to overcome the effect of noise uncertainty, a dynamic double-threshold spectrum sensing method is proposed, which adjusts its thresholds according to the achievable maximal detection probability. The results of extensive simulation demonstrate that the proposed DDEMM can achieve better detection performance than the conventional double-threshold energy sensing schemes, especially under very low SNR region.

Spectrum sensing; Energy detection; Markov model; Dynamic double-threshold

TN915

A

1009-5896(2016)10-2590-08

10.11999/JEIT151400

2015-12-14；改回日期：2016-05-16；网络出版：2016-07-04

刘玉磊 huapofeixue@sina.com

国家自然科学基金(61501496)，陕西省自然科学基金(2012JM8004)，航空科学基金(2013ZC15008)

The National Natural Science Foundation of China (61501496), The Natural Science Foundation of Shaanxi Province (2012JM8004), The Aeronautical Science Foundation of China (2013ZC15008)

刘玉磊： 男，1990年生，博士生，从事宽带移动通信组网技术研究.

梁 俊： 男，1962年生，博士，教授，从事空间信息网络与数据链技术研究.

肖 楠： 男，1987年生，博士，讲师，从事宽带移动通信组网技术研究.

扈瑜龙： 男，1989年生，硕士生，讲师，从事移动通信高效传输技术研究.

胡 猛： 男，1992年生，硕士生，从事宽带移动通信组网技术研究.