基于双广义高斯模型和多尺度融合的纹理图像检索方法

杨 娟 李永福 汪荣贵 薛丽霞 张清杨



基于双广义高斯模型和多尺度融合的纹理图像检索方法

杨 娟 李永福 汪荣贵 薛丽霞*张清杨

(合肥工业大学计算机与信息学院 合肥 230009)

纹理因素是描述图像的重要特征之一，为了准确地刻画纹理特征，增强图像的区分能力，该文提出一种基于双树复数小波域统计特征的纹理图像检索方法。首先对图像采用双树复数小波变换得到各子带系数，由于系数存在细微不完全对称分布特性，将其建模为双广义高斯模型。其次，因为各子带系数之间不完全独立也不完全冲突，存在不确定关系，所以采用模糊集合和证据理论(FS-DS)的方法，融合各子带系数特征。最后，对Brodatz和彩色纹理图像库进行仿真实验，并与多种统计建模的方法相比较。结果表明，该方法有效地提高了纹理图像的平均检索率。

纹理图像检索；双树复数小波；双广义高斯分布；模糊集合；证据理论

1 引言

随着互联网的高速发展与计算机的普遍应用，数字图像的应用越来越广泛。在面对数以万计的海量图像，如何快速、准确地检索到所需的图像成为一个急需解决的难题。目前，基于内容的图像检索(Content Based Image Retrieval, CBIR)[1]作为解决在海量图像检索的一个有效途径，成为研究图像信息处理领域的热点研究课题。基于内容的图像检索，关键在于如何将图像内容进行合理表示和相似性的有效度量。从研究现状来看，没有一种有效的描述子能够充分表达图像的内容信息。纹理是描述图像的一个重要特征，相对于形状、颜色特征，纹理特征包含信息量较多。通过纹理分析，可以获得较多的图像特性信息，因此如何通过纹理分析获得对图像内容的有效表达是一个非常值得研究的课题。

目前，纹理分析方法分为4大类，即统计分析法、结构分析法、基于模型的方法和基于频谱的方法。由于纹理特征的复杂性和多样性，这些方法都各自有其优点和局限性。统计分析方法能够描述图像的局部信息且具有一定的鲁棒性，效果相对较好。但是，该方法难以确定有效的模型参数、尺度单一，导致算法建模效果与图像信息存在偏差，不能充分刻画图像的内容信息。针对这个问题，本文旨在通过建立有效统计模型，且通过充分融合多尺度图像特征进行纹理图像检索，提高算法的检索精度。

早在20世纪70年代文献[5]就在图像空域上提出了共生矩阵的概念，由于共生矩阵提取的信息量较少，导致不能充分表达图像的纹理信息。Gabor滤波器组虽具有多分辨率功能，但参数选择复杂，计算量大。但从20世纪90年代，具有“数学显微镜”之称的小波分析不断发展，小波变换具有良好的时频局部特征和变焦特征，采用逐渐精细的时域或者空域步长，可以聚焦到分析对象的任意细节。随着小波理论的不断完善，各种小波变换被研究构造。小波变换方法在空域和频域都具有较好的局部化能力，是统计纹理特征分析的有效工具[8]。但是传统的实数小波方向分辨率差，仅包含水平、垂直及对角线方向，缺乏良好的平移不变性和方向选择性。因此本文采用文献[9]提出的双树复数小波变换(DT-CWT)[10]，提取小波系数进行统计纹理分析。

选择合理的函数模型描述小波系数分布是目前研究有效的方式之一，大部分系数分布于零点附近，因此文献[11]提出广义高斯密度函数。除此之外，由于统计采样系数零均值与假设有细小偏差，如文献[15]提出构建广义伽马模型和文献[16]对细节子带幅值系数采用贝叶斯模型[17]。虽然这些模型都能很好地刻画系数围绕零均值附近的分布情况，但是从小波系数直方图的细微观察分析中可以发现，小波域系数密度函数不完全符合对称分布，从部分纹理图像的小波系数分布直方图显得尤为突出，针对此问题本文引入了双广义高斯混合模型；此外，各尺度下子带小波系数之间密度函数并非独立分布，存在不确定关系，因此针对以上问题进行研究。

为了准确地提取有效的纹理描述子，本文提出一种基于模糊集和证据理论(FS-DS)的信息融合方法，通过该方法融合小波域子带的系数特征形成一种有效的纹理分析统计特征，由此实现对纹理图像的检索。具体思路：首先经过双树复数小波变换得到子带系数矩阵，并建模为双广义高斯模型，采用反函数曲线拟合的方法进行参数估计，克服小波系数分布函数不完全对称问题；针对各子带之间存在不确定关系，采用模糊集合和证据理论(FS-DS)的方法融合各子带系数特征进行纹理图像检索。

2 双树复数小波系数的双广义高斯分布模型

在图像处理领域的实际应用中，数据分布是未知概率密度函数的近似拟合建模，并且建模的误差程度和时间复杂度是考核建模的重要标准。目前，广义高斯密度函数(GGD)已经在小波域广泛应用。

离散小波变换(DWT)会产生较大混叠，带来畸变，严重影响小波系数表征原图像纹理特征的能力。导致这种缺陷的原因表现在两个方面：平移变化性和弱的方向选择性，为了克服这些弊端，文献[9]提出了DT-CWT变换。得到任何一个子带小波系数的期望值基本近似为零，因此本文采用零均值双广义高斯分布来描述双树复数小波子带系数分布，分别对小波域系数的正数部分和负数部分进行函数拟合，其中广义高斯密度函数为

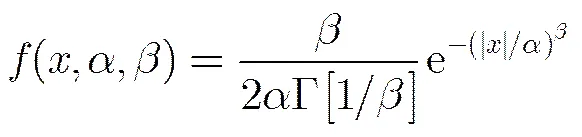
其中，

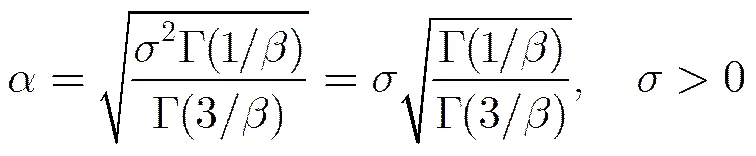
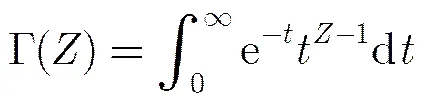
图1(a)和(b)绘制的是来自Brodatz纹理图像库的D26.gif纹理图像以及该图像的子带系数直方图。根据直方图形状可以看出其分布接近零均值GGD函数密度分布曲线，在之间基本满足对称分布，符合GGD模型，但是在之外能够稍微显现分布不对称情况。

图1(c)和(d)绘制的是来自Brodatz纹理图像库的D55.gif纹理图像以及该图像的双树复数小波子带系数直方图。从这幅纹理图像的小波域系数统计直方图就可以很明显地看出分布的不完全对称情况，以零均值为中心，在负数域的系数密度分布明显大于在正数域的密度分布。

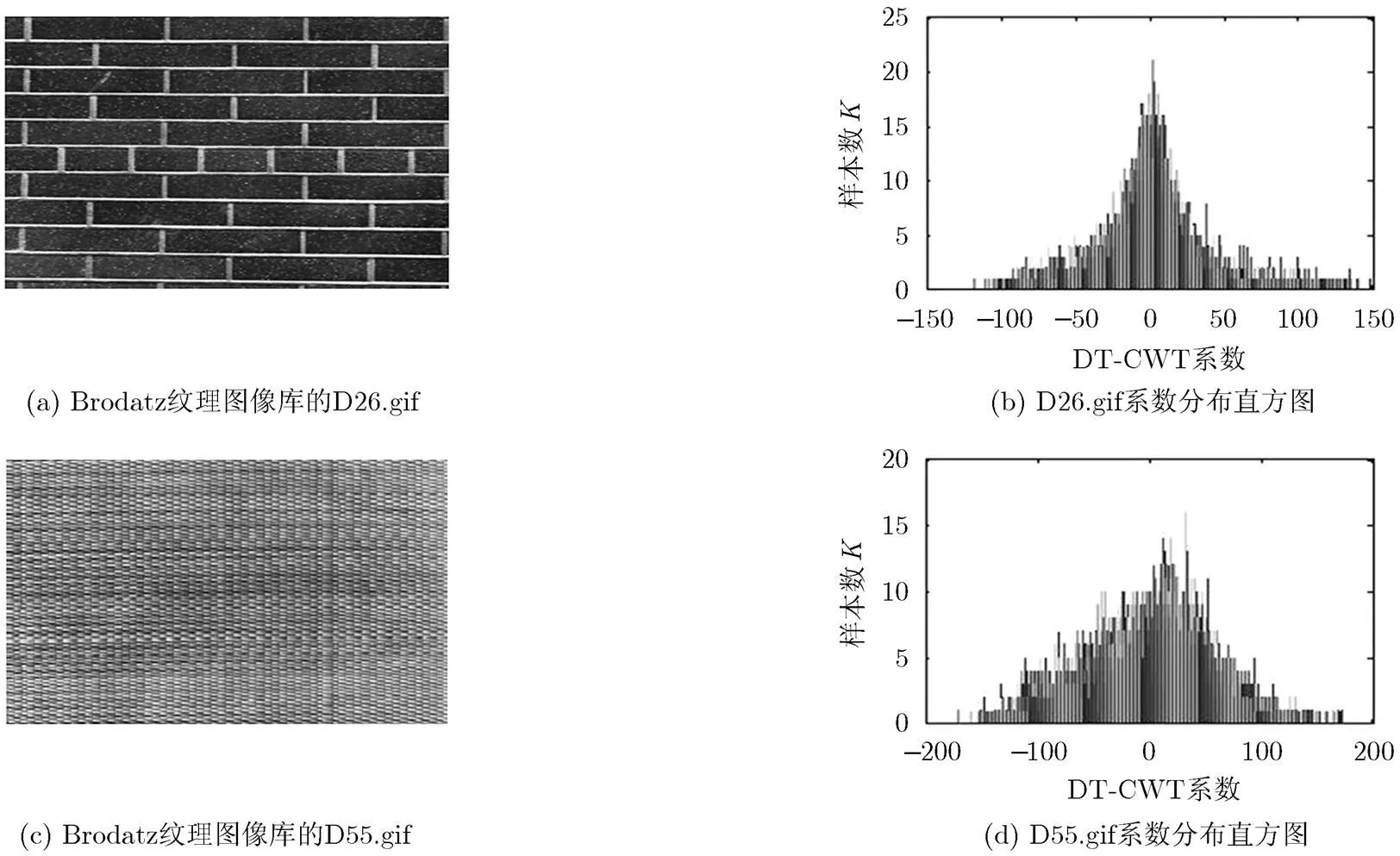
图1 Brodatz纹理图像以及双树复数小波系数直方图

双树复数小波变换与一般实数小波变换类似，得到的系数矩阵中，大部分系数分布于零域附近，但部分纹理图像存在上述不完全对称问题，因此本文引入了双广义高斯混合模型，在负数域和正数域分别进行拟合广义高斯分布函数。

双广义高斯混合模型具体建模如下：

(1)依据DT-CWT原理，对图像进行多层小波变换，提取每幅图像的双树复数小波各子带系数；

(2)采用矩阵分解的方法将子带系数矩阵进行正负系数分离，即=+，其中是原系数矩阵，是正数部分，是负数部分；

(3)将两个分解后的系数矩阵重构为对称分布，和-组合，和-组合，形成了两个标准对称分布，分别采用广义高斯拟合系数密度分布函数。

3 参数估计

广义高斯密度函数的尺度参数和形状参数的估计算法复杂性导致其在实际应用中的局限性问题，典型的估计方法有3种：矩估计法、熵匹配法和最大似然(ML)估计法，其中最大似然估计法相对较好，但是由于反函数的解析式很难求得，需要迭代计算，计算效率很低。本文借助基于反函数曲线拟合的GGD形状参数和尺度参数方法[18]，使算法效率大大提高。由于GGD对称分布，其一阶原点矩为零，故采用绝对矩方法对参数估计推导得到：

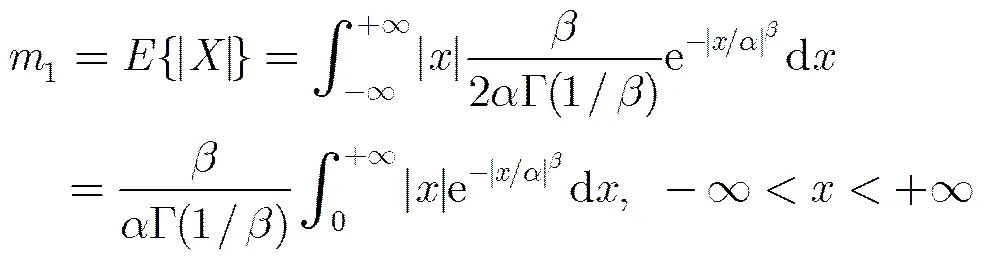
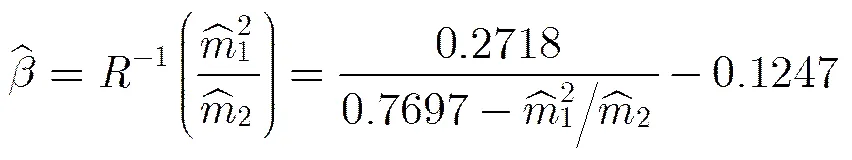
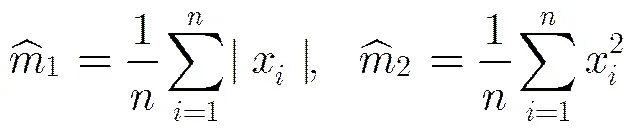
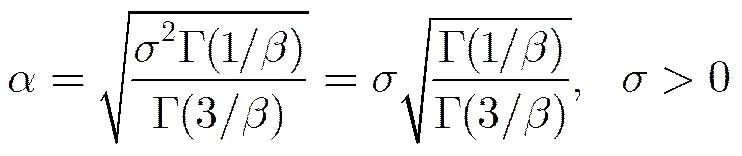
采用曲线函数拟合的反函数快速估计双广义高斯分布模型中形状参数和尺度参数，实验证明在不影响参数估计精度的条件下，大大提高了检索的效率，同时降低了时间复杂度。

4 基于FS-DS特征融合的纹理图像检索方法

文献[19]提出了基于模糊集合和证据理论(FS- DS)信息融合方法，利用模糊集合理论中的隶属函数获得各信息源的局部决策，并采用“决策距离”的概念对各个信息源的一致性进行检验。该方法利用模糊集合理论隶属度函数范围的优点，以模糊置信距离测度的大小表示数据之间的相互支持程度，解决了支持概率的绝对化问题。该方法定义不确定信息的模糊支持概率，由隶属函数得到各个信息源的可信度，对各个信息源的信任程度进行量化处理，利用上述结果的得到证据理论中的mass函数，最后利用D-S准则对多信息源进行融合，使融合结果更加准确、可信。

针对双树复数小波变换的各子带系数的统计特征，同一幅图像各子带之间存在不完全独立，同样也不完全冲突，所以采用模糊集合和证据理论(FS- DS)[19]方法能有效地融合各子带特性。在经过双树复数小波变换的统计特征时，利用DT-CWT变换对图像进行分解生成多分辨率图像，在每个分辨率尺度上的图像被分解成8个子带图像，其中2个为低通滤波子图像，6个为高通滤波子图像。低频信息反映了纹理的基本信息，高频信息反映了纹理的细节信息。

由于各子带系数之间的不确定关系，所以各子带中包含的纹理信息也有所不同，为了能客观衡量各自在纹理信息描述中的分量，采用模糊集合理论进行计算。首先为了各子带系数在同分布下进行比较，进行归一化处理：

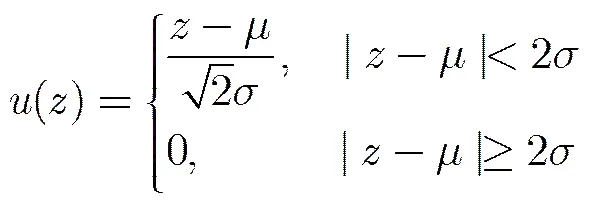
根据公式：

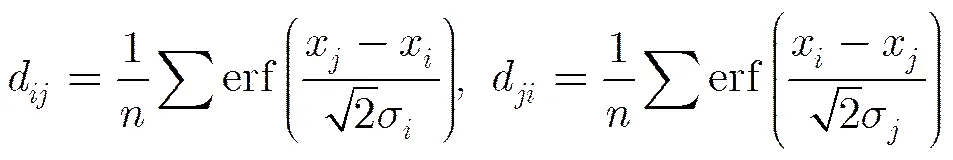
其次对查询图像和候选图像的个子带系数Dual-GGD分布的参数，构造个信任函数，利用文献[15]提出的SKLD公式推导方法构造信任函数：

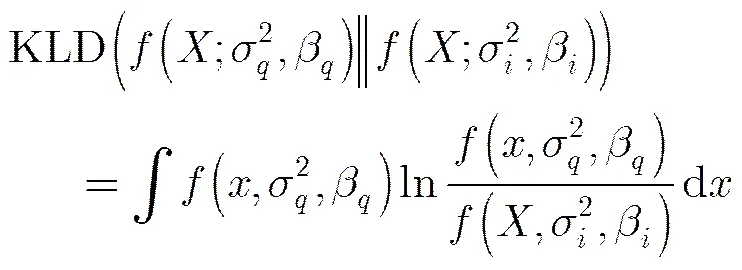
构造信任函数如下：

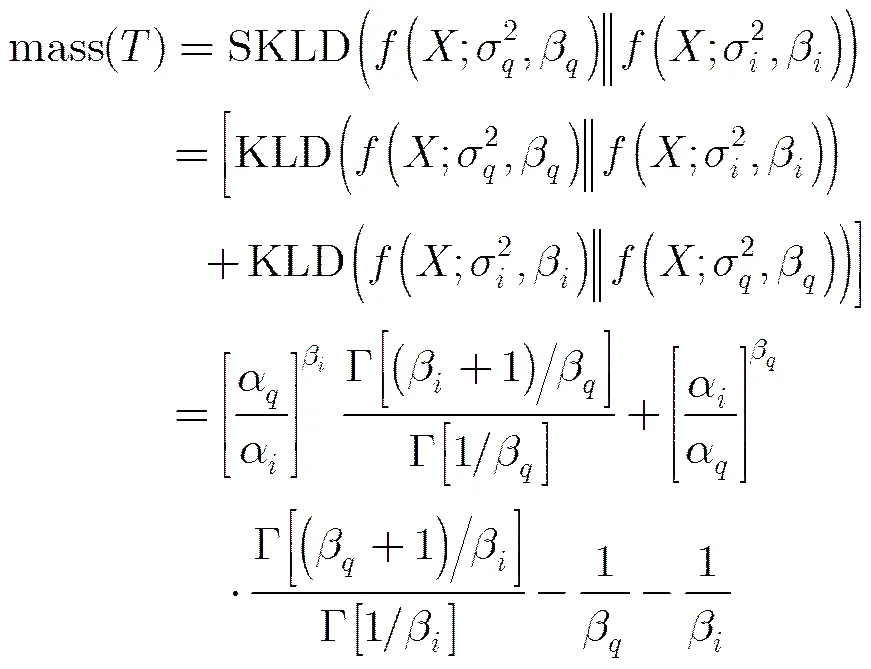
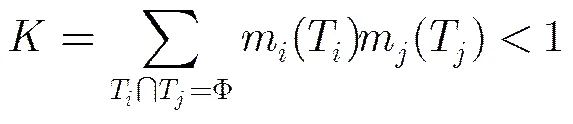
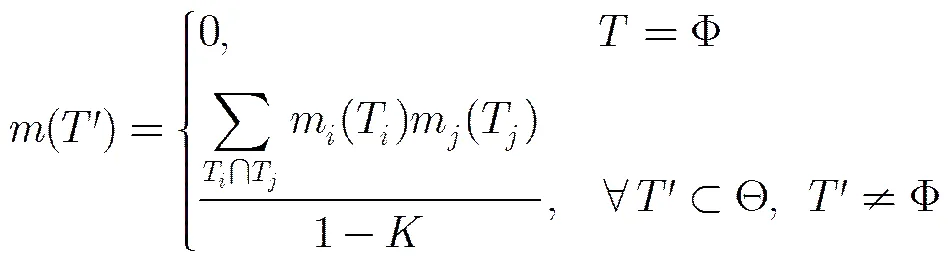
综上所述，基于双广义高斯模型和多尺度融合的纹理图像检索方法的算法步骤描述如下：

步骤1 随机地从测试图像库中抽取查询的纹理图像样本，进行检索实验；

步骤2 图像经过双树小波变换得到各子带系数矩阵，根据系数分布关于零点的不完全对称情况，零作为分布的界点，可以采用矩阵分解实现正负系数分离；

步骤3 对各子带系数矩阵进行建模，采用反函数曲线拟合的方法求取对应的双广义高斯模型的参数；

步骤4 对查询图像与测试图像库图像子带系数分别进行归一化，通过模糊集合理论计算各子带之间的置信距离测度，即相互支持程度，确定各子带先后融合次序；

步骤5 将SKLD公式计算结果作为各子带对应的信任函数值，根据步骤4中的顺序依次融合各子带的信任函数值。其最终结果为相似度度量值并进行排序，输出前个最高相似度图像。

5 实验结果与分析

在测试纹理图像检索实验时，一个查询的纹理图像样本应该是随机的从测试图像库中选取，检索结果根据最终相似性从大到小依次排列。本文将评估检索性能的平均检索率()，其计算公式如式(14)：

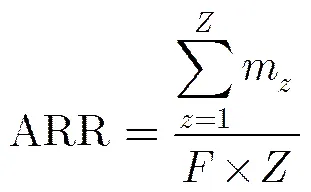
5.1 基于DT-CWT系数的双广义高斯模型

提取图像的纹理特征，在多尺度变换域，准确有效地提取各子带的统计分布特征是非常重要的。通过观察系数矩阵密度函数分布直方图，针对纹理图像系数矩阵密度分布不严格对称问题，本文提出了基于双广义高斯混合模型(Dual-GGD)提取纹理特征。

在GGD参数估计中，文献[11]采用Newton- Raphson迭代的方式作为参数估计的方法，但精度存在问题。文献[21]提出最大似然估计方法(ML)中，同样采用Newton-Raphson迭代方法估计形状参数,的初始值由偏度查询表获得，这种方法能够有效地估计分布参数，但迭代算法运算时间复杂度与收敛性密切相关，一般都较耗费时间。除此之外，如图2所示，该直方图是Brodatz纹理图像库的D18.gif小波域系数分布直方图，采用这种方法不能对有些子类图像准确建模，产生此问题的原因是由于Newton-Raphson迭代方法对初始值选取要求较高，只有当所选的初始值和真实值相接近时，估计的结果才相对准确。

根据图1中显示的两张来自Brodatz纹理图像库的D26.gif和D55.gif纹理图像，并与单广义高斯模型曲线进行比较。具体实验如下：采用DT-CWT原理，对图像进行双树复数小波变换，提取每幅图像的各子带系数，通过统计子带系数分布直方图近似代替小波系数概率分布函数，检验概率分布曲线是否近似双广义高斯分布模型，并且与单广义高斯密度分布函数曲线作比较。模拟的实验结果如图3，图4，图5所示。

通过对图3和图4实验结果分析，GGD和Dual- GGD实验结果中函数曲线差异较小，原因在于原图的小波域系数基本符合对称分布，所以差异不大。但是从图5来自Brodatz纹理图像库的D55.gif的拟合曲线存在较为明显的左右差异，位于零界点左边分布密度略大，正如图1(d)所示。综上通过对实验结果的分析，双广义高斯混合模型能够克服纹理图像小波域系数分布不对称情况，合理描述图像内容信息，充分地刻画纹理特征。

5.2 基于FS-DS特征融合的纹理图像检索

在多尺度变换域，低频信息反映了纹理的基本信息，但是高频子带的统计分布特征对于描述图像的纹理信息也非常重要。为此本文根据各子带系数之间存在的不确定关系，在纹理图像检索时，利用模糊集合和证据理论(FS-DS)的方法融合各子带系数纹理特征，求得综合相似程度，弥补假定各细节子带是独立同分布所带来的偏差，与距离直和法(the sum of distance)进行对比实验。

为了便于比较，在下面的检索试验中都采用对称KL距离(Symmetrized Kullback-Leibler Distance, SKLD)[15]，目的是为了实现两个图像的统计模型差异的更均衡测量。实验结果如图6所示，图6(a)中，横坐标表示单尺度分解下各方向子带的数量，其中“1”表示的方向自带数为2，“2”表示方向子带数为6，“3”表示的方向子带数为8；图6(b)中，横坐标表示3个尺度分解下各方向子带的数量，其中“1”表示的方向子带数排列为(2,2,2)，“2”表示的方向子带数为(2,2,6)，“3”表示方向子带数为(2,6,6)，“4”表示方向子带数为(2,6,8)，下文的实验结果显示均采用此标注方法。实验结果说明，采用本文的融合各子带信息可以较好地改善纹理图像检索的性能。

本文提出的基于双广义高斯模型和多尺度纹理图像检索方法的性能也和其他的检索方法进行了对比。实验结果如图7所示。能量方法(Energy)采用的特征是子带系数的均值和方差，相似性度量采用归一化欧氏距离[22]；广义伽马分布方法(Generalized Gamma Density (Gamma))采用的基于广义伽马模型统计小波域系数特征[14]；广义高斯分布方法(Generalized Gaussian Density(Gauss))方法采用的是单广义高斯模型统计子带系数特征[23]；WD方法采用的特征为子带系数的Welbull分布参数；它们的相似性度量均采用SKLD方法，FS-DS是本文的设计的检索方法。根据实验结果图7所示，本文算法具有较好的检索性能。此外，表1所示的是典型的3层分解(4,8,8)情况下各种纹理图像检索方法的实验结果，其中包含本文检索结果还和其他方法(即Kwitt方法[21]和Gabor方法)的结果进行了对比，这些方法采用了和本文相同的检索性能的评价标准。

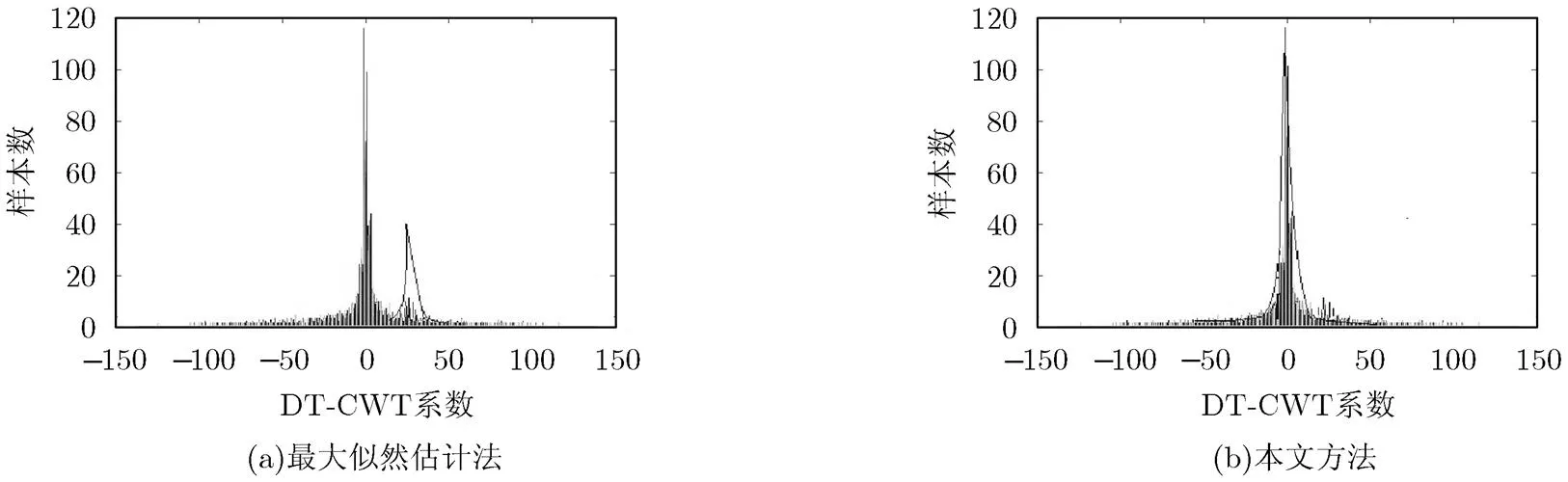
图2 两种参数估计方法的拟合性能比较

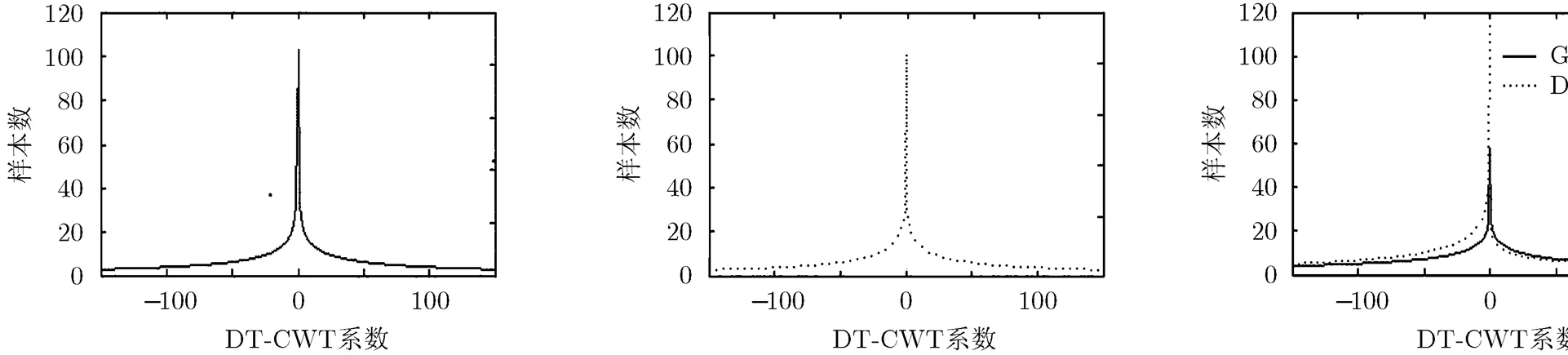
图3 D26.gif的GGD拟合曲线     图4 D26.gif的Dual-GGD拟合曲线     图5 D55.gif的曲线拟合

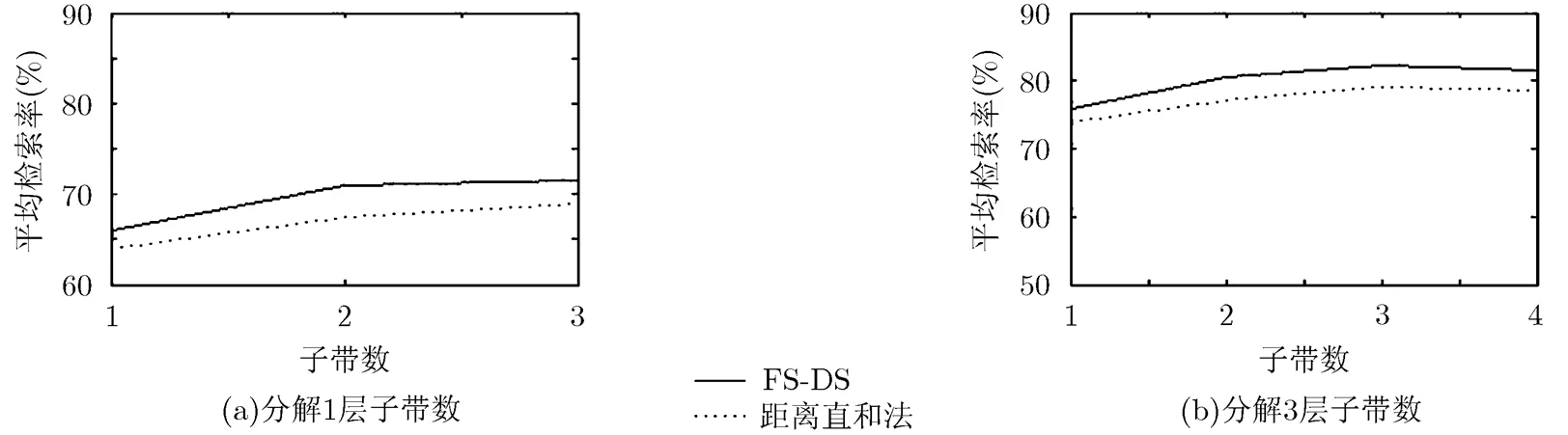
图6 不同子带间信息融合方法检索性能比较

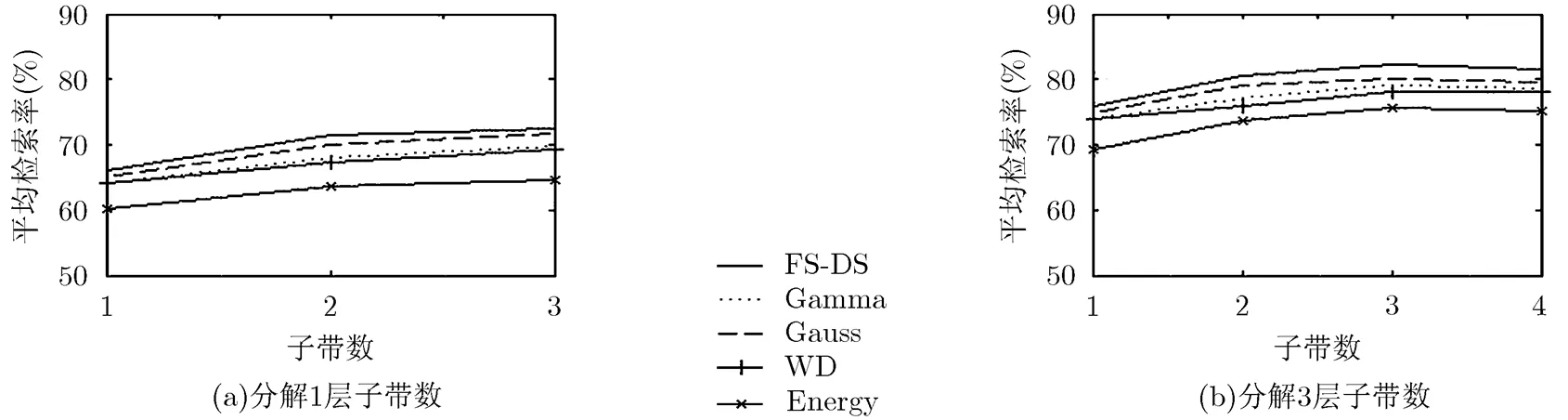
图7 不同方法下的检索性能比较

Gabor变换在特征提取需要较高的运算复杂度，并且传统的小波变换方法具有平移不变性性和弱的方向选择性等缺点。基于以上的问题，本文引入了双树复数小波变换(DT-CWT)，根据文献[9]有效地提高了检索图像的方向选择性和旋转不变性的特点。通过表1结果显示，采用FS-DS融合双树复数小波变换域各子带系数特征进行检索的性能明显提高，主要是本文算法提取了更加丰富的纹理特征信息，并且有效地融合了各子带之间对检索决策的不确定关系。

表1基于Brodatz纹理库的检索性能比较

方法FS-DSGammaGaussWDEnergyKwittGabor 平均检索率(%)82.2479.2179.5077.9875.7080.2174.37

为了进一步客观地评价本文算法的实用性和有效性，对彩色纹理图像进行对比实验。由于彩色图像属于多通道图像，首先需要进行通道分离，直接采用RGB 3通道转化为灰度纹理图像。本文挑选多组彩色纹理图像，分为28个类别，每组由20多幅相似纹理图像构成的彩色纹理图像的实验库。随机的从测试图像库中选取一个查询图像，进行纹理检索实验。其实验结果依次显示前个相似图像纹理图像，为了避免偶然性，同上述方法，并通过多次重复试验得到平均检索率。在相同的实验环境下，与其它检索算法进行比较。

表2所示的是在彩色纹理图像RGB 3通道分解下的各种纹理图像检索方法的实验结果，其中包含本文检索结果还和其他方法(即Gamma, Gauss, WD, Energy, Kwitt和Gabor方法)的结果进行了对比，这些方法采用了和本文相同的检索性能的评价标准。

通过实验数据分析，在彩色纹理图像检索中，Gamma法和Gauss法相比其他方法有一定程度的提高，但本文方法具有更高效的检索性能，在平均检索率上均有3%~5%不同程度的提高。除此之外，彩色纹理图像相对于单通道灰度纹理图像具有更加丰富图像内容信息，平均检索率的精度也略有增加。综上所述，本文方法在彩色纹理图像检索应用中同样具有良好的检索性能。

6 结论

本文提出一种基于双广义高斯模型和多尺度融合纹理图像检索算法。通过实验结果表明：在双树复数小波变换下，采用双高斯混合模型有效地保证了小波域系数密度分布不完全对称的情况，而且采取曲线拟合的参数估计方法，有效地保证了估计算法的效率。此外，本文还提供了通过模糊集合和证据理论(FS-DS)的方法融合各子带系数之间的不确定关系，改善了检索精度。与目前多种方法进行对比实验，本文算法充分利用了所有细节子带的信息，以及有效融合各尺度子带系数特征，多尺度融合更好地刻画了纹理图像的特征，增强了纹理图像的区分能力，有效地改善了检索性能。

表2基于彩色纹理库的平均检索率比较

方法FS-DSGammaGaussWDEnergyKwittGabor 平均检索率(%)86.1780.7683.4380.5074.6481.1976.15

[1] GUO Jingming and PRASETYO H. Content-based image retrieval using features extracted from halftoning-based block truncation coding[J]., 2015, 24(3): 1010-1024. doi: 10.1109/TIP.2014. 2372619.

[2] GUO Xian, HUANG Xin, and ZHANG Liangpei. Three- dimensional wavelet texture feature extraction and classification for multi/hyperspectral imagery[J]., 2014, 11(12): 2183-2187. doi: 10.1109/LGRS.2014.2323963.

[3] HONG Xiaopeng, ZHAO Guoying, PIETIKAINEN M,Combining LBP difference and feature correlation for texture description[J].,2014, 23(6):2557-2568. doi: 10.1109/TIP.2014.2316640.

[4] ARASHLOO S R and KITTLER J. Dynamic texture recognition using multiscale binarized statistical image features[J].,2014, 16(8): 2099-2109. doi: 10.1109/TMM.2014.2362855.

[5] HARALICK R M, SHANMUGAM K, and DINSTEIND I. Texture feature for image classification[J].,,, 1973, 3(6): 610-621.

[6] LI Chaorong, DUAN Guiduo, and ZHONG Fujin. Rotation invariant texture retrieval considering the scale dependence of Gabor wavelet[J]., 2015, 24(8): 2344-2354. doi: 10.1109/TIP.2015.2422575.

[7] RIAZ F, HASSAN A, REHAN S,Texture classification using rotation- and scale-invariant Gabor texture features[J]., 2013, 20(6): 607-610. doi: 10.1109/LSP.2013.2259622.

[8] SCHARFENBERGER C, WONG A, and DAVID A. Clausi. Structure-guided statistical textural distinctiveness for salient region detection in natural images[J].,2015, 24(1): 457-470. doi: 10.1109/TIP.2014.2380351.

[9] KINGABURY N. Complex wavelets for shift inavriant analysis and filtering of Signals[J]., 2001, 10(3): 234-253.

[10] ANANTRASIRICHAI N, BURN J, and BULL D R. Robust texture features based on undecimated dual-tree complexwavelets and local magnitude binary patterns[C]. 2015 IEEE International Conference on Image Processing (ICIP), Québec, 2015: 3957-3961.

[11] DO M N and VETTLI M. Wavelet-based texture retrieval using generalized gaussian density and kullbackleiber distance[J]., 2002, 11(2): 146-158. doi: 10.1109/83.982822.

[12] LASMAR N E and BERTHOUMIEU Y. Gaussian copula multivariate modeling for texture image retrieval using wavelet transforms[J]., 2014, 23(5): 2246-2261. doi: 10.1109/TIP.2014. 2313232.

[13] ARANI M N and ZHANG Xiaoping.Generalized Gaussian mixture conditional random field model for image labeling[C]. 2014 IEEE Global Conference on, Signal and Information Processing (GlobalSIP), Atlanta GA, 2014: 1068-1072.

[14] ALLILI M S, BAAZIZ N, and MEJRI M. Texture modeling using contourlets and finite mixtures of generalized Gaussian distributions and applications[J]., 2014, 16(3): 772-784.doi: 10.1109/TMM.2014. 2298832.

[15] CHOY S K and TONG C S. Statistical wavelet subband characterization based on generalized Gamma density and its application in texture retrieval[J]., 2010, 19(2): 281-289. doi: 10.1109/TIP. 2009.2033400.

[16] KWITT R, MEERWALD P, and UHL A. Efficient texture image retrieval using copulas in a Bayesian framework[J]., 2011, 20(7): 2063-2077. doi: 10.1109/TIP.2011.2108663.

[17] COMBREXELLE S, WENDT H, DOBIGEON N,Bayesian estimation of the multifractality parameter for image texture using a whittle approximation[J]., 2015, 24(8): 2540-2551. doi: 10.1109/TIP.2015.2426021.

[18] WANG Taiyue, LI Hongwei, LI Zhiming,A fast parameter estimation of generalized Gaussian distribution[C]. 2006 8th International Conference on Signal Processing, Beijing, 2006, 1: 1-4. doi: 10.1109/ICOSP.2006.345546.

[19] 韩峰, 杨万海, 袁晓光. 基于模糊集合的证据理论信息融合方法[J]. 控制与决策, 2010, 25(3): 449-452. doi: 10.13195/j.cd. 2010.03.132.hanf.023.

HAN Feng, YANG Wanhai, and YUAN Xiaoguang. Evidence theory information fusion method based on fuzzy set[J]., 2010, 25(3): 449-452. doi: 10.13195/ j.cd.2010.03.132.hanf.023.

[20] DANIEL C. On the solution of linear differential equations with singular coefficients[J]., 1982, 46(2): 310-323.

[21] KWITT R and UHL A. Lightweight probabilistic texture retrieval[J], 2010, 19(1): 241-253.doi: 10.1109/TIP.2009.2032313.

[22] MANJUNATH B S and MA W Y. Texture feature features for browsing and retrieval of image data[J]., 1996, 18(8): 837-842. doi: 10.1109/34.531803.

[23] QU H J, PENG Y H, and SUN W F. Texture image retrival based on Contourlet coefficient modeling with generalized Gaussian distribution[J]., 2007, 4683: 493-502.

Texture Image Retrieval Method Based on Dual-generalized Gaussian Model and Multi-scale Fusion

YANG Juan LI Yongfu WANG Ronggui XUE Lixia ZHANG Qingyang

(,,230009,)

Texture factor is one of the most important characteristics in the image description. In order to describe the texture feature accurately, and enhance image distinguish ability, a method of texture image retrieval is proposed based on Dual-Tree Complex Wavelet Transform (DT-CWT) in this paper. Firstly, each sub-band coefficient is obtained by DT-CWT, because the coefficient distribution exists slight incomplete symmetrical feature, which is modeled as dual-generalized Gaussian model. Secondly, there is incomplete independent anduncertain conflict between the sub-band coefficients, therefore the Fuzzy Set and Dempster-Shafer (FS-DS) evidence theory are applied to blending the characteristics of each subband coefficients. The performance of the propose algorithm is tested on the Brodatz and color texture image library, and also compared with a variety of statistical modeling methods. The experimental results demonstrate that the proposed method can improve the average retrieval rate of the texture images effectively.

Texture image retrieval; Dual tree complex wavelet; Dual-generalized Gaussian distribution; Fuzzy set; Evidence theory

TP391.4

A

1009-5896(2016)11-2856-08

10.11999/JEIT160181

2016-03-01；改回日期：2016-07-01；

2016-09-08

薛丽霞 xlxzzm@163.com

中国博士后基金(2014M561817)，安徽省自然科学基金(J2014AKZR0055)

China Postdoctoral Fund (2014M561817), The Natural Science Foundation of Anhui Province (J2014AKZR 0055)

杨 娟： 女，1983年生，讲师，研究方向为视频信息处理、视频大数据处理技术等.

李永福： 男，1991年生，硕士生，研究方向为图形图像处理与计算机视觉.

汪荣贵： 男，1966年生，教授，研究方向为智能视频处理与分析、视频大数据与云计算等.

薛丽霞： 女，1976年生，副教授，研究方向为视频大数据检索与分析.

张清杨： 男，1990年生，博士生，研究方向为优化分析处理.