基于BP神经网络的自适应伪最近邻分类

曾 勇 舒 欢 胡江平 葛月月



基于BP神经网络的自适应伪最近邻分类

曾 勇 舒 欢*胡江平 葛月月

(电子科技大学自动化工程学院 成都 611731)

在伪最近邻(PNN)分类算法中，待分类样本点与每一类样本集中各个近邻的距离加权系数都是主观确定的，这就使得算法得不到最优距离加权值。针对这一问题，该文提出一种基于BP神经网络的自适应伪最近邻分类算法。首先通过计算待分类样本点与每一类样本集中各个近邻的距离值，并将其作为BP神经网络的输入。然后根据BP神经网络输入与输出之间的映射来自适应确定相应的距离加权值。最后由BP神经网络的输出值判别样本类别号。实验结果表明，该算法能够自适应地调节距离加权系数，同时还能有效地改善分类准确率。

伪最近邻分类；BP神经网络；自适应

1 引言

为了解决PNNR存在的不足，本文提出了一种新的分类方法：基于BP神经网络的自适应伪最近邻分类方法(Adaptive pseudo Nearest Neighbor classification based on BP neural network, BPANN)，根据同类样本特征相似，而不同样本特征值差异较大这一特性来计算测试样本在每一个类别中的个近邻点，充分利用了测试样本在每一类原型样本集里的多个近邻信息，将计算出的测试样本与各近邻点间的距离值作为网络输入，并通过BP神经网络输入和输出之间的映射自适应地训练距离加权系数，使得分类器的分类精度得以提高。

本文其余部分组织如下：第2节介绍伪最近邻分类算法；第3节将给出本文所提出的BPANN的具体算法步骤以及分类器设计；第4节是实验及结果分析；最后是本文结论。

2 伪最近邻分类

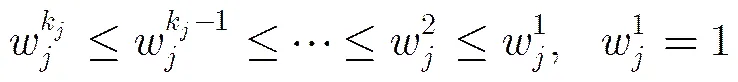
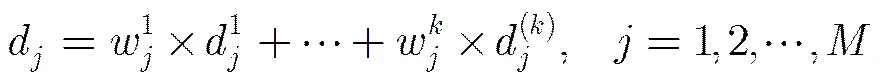
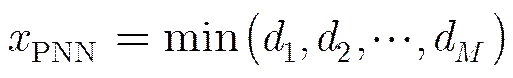
由文献[17]提出的伪最近邻规则PNNR(Pseudo Nearest Neighbor Rule)如下：一个测试样本对给定，则伪最近邻分类规则把测试样本分配为其伪最近邻所属的类别，如果有多个伪最近邻，则在其中随机选择一个，并把其对应的类别指定给测试样本。

实验表明伪最近邻分类方法的分类性能优于传统的最近邻分类方法与传统的近邻分类方法，也优于传统的距离加权的近邻分类算法[17]，但由于其中的距离加权系数都是人为主观确定的，并不能得到较优的距离加权值，为此本文提出了一种基于BP神经网络的自适应伪最近邻分类的方法。

3 基于BP神经网络的自适应伪最近邻分类

基于BP神经网络的自适应伪最近邻分类是伪最近邻分类方法的扩展，与PNN分类算法不同的是，BP神经网络分类器的输入不是待分类样本点的特征值，而是待分类样本在每一类样本集中的各个近邻的距离值。并且距离加权值不需要人为确定，而是由BP神经网络输入和输出之间的映射自适应确定，同时对每类原型样本自适应的设计其相应的分类器，从有效的样本资料中得到尽可能多的信息，使其获得更好的分类效果。图1显示的是自适应伪最近邻分类器的训练原理图，其中输入数据是训练数据集，分别各自表示属于类的原型样本数，表示其对应个近邻按升序排列的与测试样本的距离，表示个分类器的输出值。

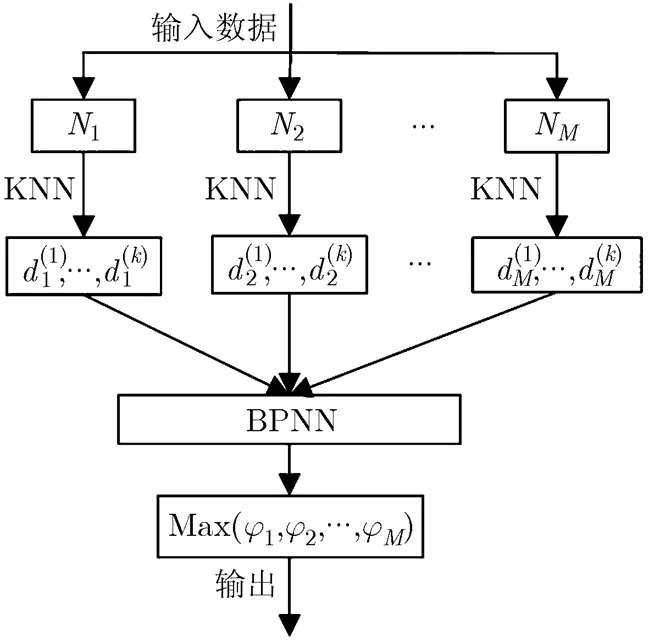
图1 自适应伪最近邻分类器训练原理图

3.1 BPANN模型的参数设置

BP神经网络具有良好的容错性、与人脑相似的高度并行性以及联想记忆功能，容错能力和自适应学习都较强，可以实现从输入到输出的非线性映射。应用于近邻分类的BP神经网络分类器，必须结合数据集的情况设计，并在试验中不断改进，才能训练出泛化性能好的模式分类器。所以，必须选择适当大小的网络结构，网络太小不能解决问题，太大则推广能力差。本文中，BP神经网络在样本训练阶段通过附加动量法来调整层与层之间的权值和阈值，从而通过网络输入输出之间的映射自适应的调节距离加权权值，同时针对样本数据的数据类别自适应的设计其相应的分类器，以便选出较优的分类器。

(1)输入与输出层节点数确定：BP网络的输入、输出层维数需要根据实际要求而定，本实验中，若样本预处理时采用的是近邻，那么输入层的维数就为；而输出层输出的则是样本的相似度即新的距离加权和，因此输出层的维数为1。

(2)隐层层数的选择及隐层节点数：根据戈尔莫戈罗夫(Kolmogorov)定理，一个3层的BP网络足以完成任何从输入到输出的连续映射，因此，我们采用具有一个隐层的3层BP神经网络。隐节点数目的选择是一个比较复杂的问题，目前确定隐节点数的方法有很多种，主要有修剪方法、复杂性调整方法、增益方法、进化方法、自适应方法[18]等。在大量实验的基础上，这里选择式(4)作为参考。

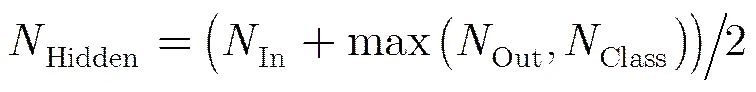
(3)激活函数的选择：神经元的激活函数一般选用Sigmoid函数，经过大量实验对比，最终我们选取式(5)所示logistic函数作为激活函数。

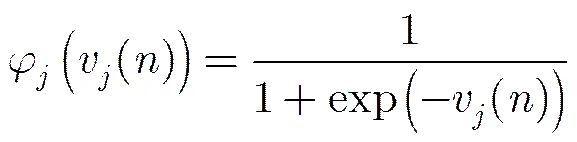
(4)初始权值的选取：因系统的非线性性使初始权值对学习是否收敛关系很大，故而希望初始权值在输入累加时使每个神经元的状态值接近于零。一般，初始权值取随机数，而且权的值要求比较小。

(5)学习率以及冲量项的选择：原则上，只要学习率足够小以保证收敛，但实际上学习率可以影响到最后的网络性能。而冲量项的目的在于：允许当误差曲面中存在平坦区时，网络可以以更快的速度学习，增加了学习过程的稳定性。对于我们所用的Sigmoid型网络，可以首先将学习率设为0.2，冲量项设为0.9，然后可以在学习过程中适当的改动。

3.2 BPANN分类方法的实现

基于BP神经网络的自适应伪最近邻分类方法实现的流程图如图2所示。

由于在实际应用中用于训练的样本各元素之间取值范围不可能完全一致，这就给网络的训练带来很大不便，不仅加大了逼近函数的波动性，使网络训练速度下降，而且容易造成网络训练失败。因此先对数据进行适当的预处理是非常重要的，这在一定程度上可以加速训练，提高训练的成功率。样本集经过预处理后，便将其送入BP神经网络中进行网络训练。对于一个数据集中个可得的训练样本，令分别表示对应于属于类的训练样本数。

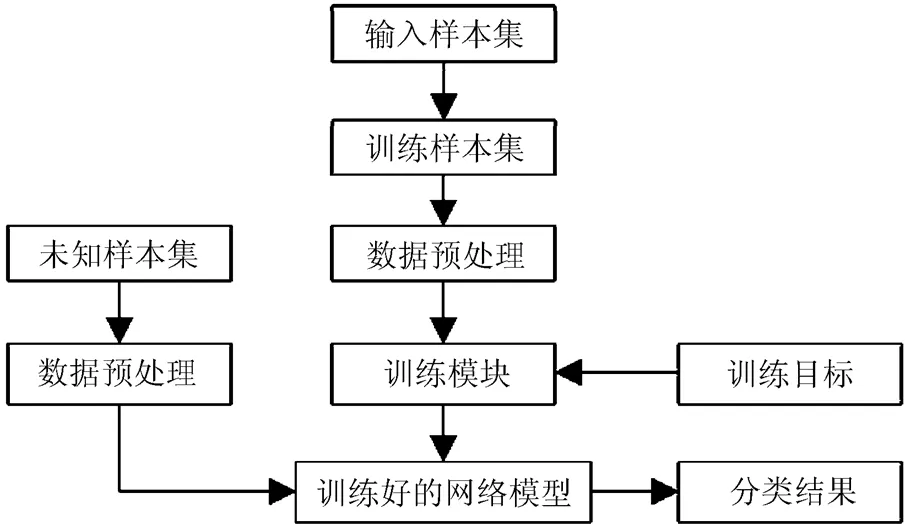
图2 基于BP神经网络的自适应伪最近邻分类方法实现流程

BPANN的具体步骤如下：

步骤1 将样本数据集(data)分为训练集(trainsam)和测试集(testsam)，进行数据预处理。计算每个训练样本点在每一类训练样本中的个近邻，以及到各个近邻的距离，并将其按升序排列为，对每一类样本数据经过归一化处理后计算对应的正例、反例，类的正例、反例个数分别为，其中正例指在类内寻找的样本点，反例指从类间寻找的样本。将每一类的正例、反例作为BP神经网络的输入，表示为，并且数据集中每一类样本分别对应一个BP网络分类器，类共对应个分类器。

{

初始化BP神经网络，即设定网络参数。其中输入层到隐含层与隐含层到输出层的权值和偏置分别表示为，将它们分别取随机数。

完成步骤3-步骤5。

}

步骤3 预处理后的数据送入网络中进行训练，得到新的权值以及偏置。

本文采用附加动量法来作为权值和偏置的学习算法，其权值学习公式为

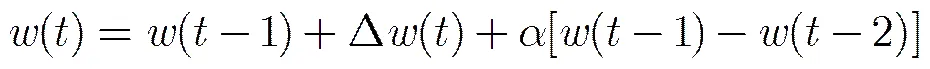
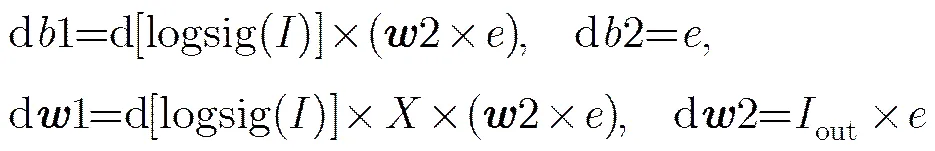
式中是网络输出的误差，用于权值和偏置的修正，是网络隐含层的输出，,

步骤4 将预处理后的测试样本送入已经训练好的网络中进行分类，找出网络输出值中的最大值，也就是新的伪最近邻，并将测试样本分到最大值对应的的索引类。

4 实验结果及分析

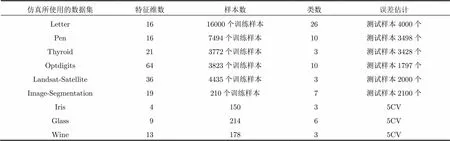
实验是在MATLAB7.11.0环境下实现，采用了机器学习库UCI[19]上的9个数据集。所使用的数据介绍见表1。数据集Letter, Pen, Thyroid, Optdigits, Landsat-Satellite和Image-Segmentation，其训练样本集与测试样本集已被预先指定。而其余的3个数据集，通过5倍交叉验证来选择训练集与测试集，其中对于数据集采用的距离度量是欧几里得距离。

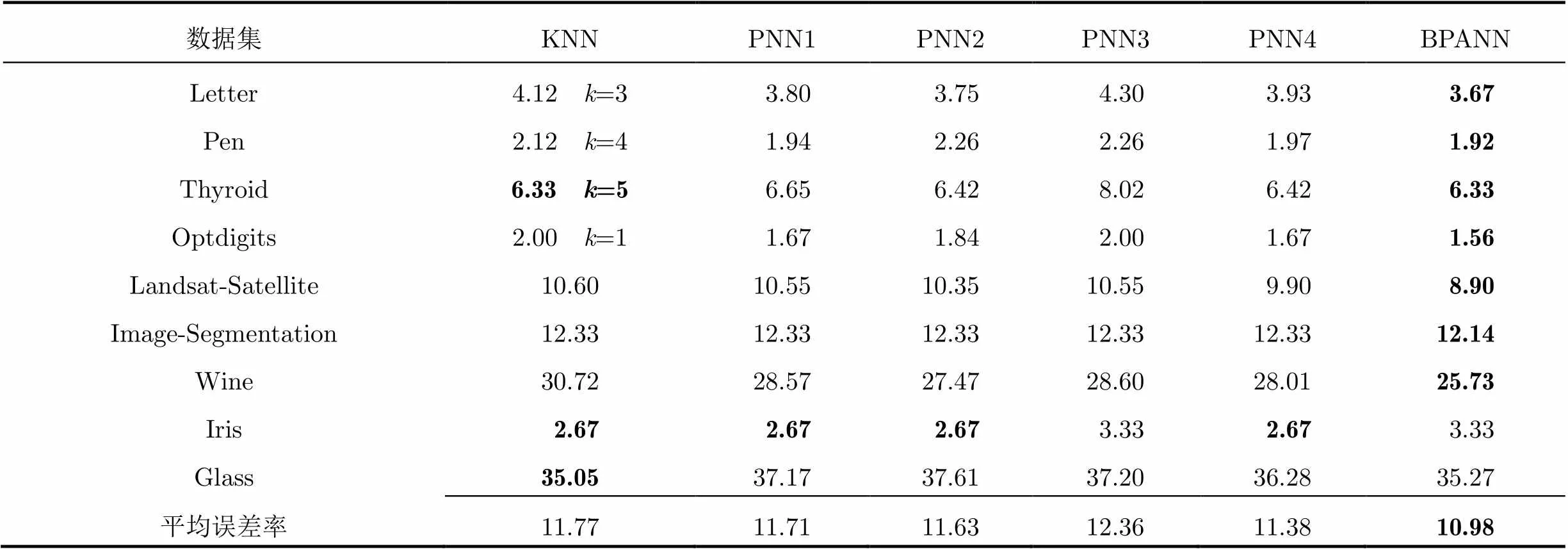
现在用BPANN与PNN以及传统的KNN一起对机器学习库UCI[19]上的9个数据集进行分类，其中PNN1, PNN2, PNN3, PNN4分别是距离逆加权、指数衰减距离加权、线性距离逆加权、倒数距离加权的伪最近邻分类，分类结果见表2。对每一个数据集，几种分类方法中最好的分类结果用黑体表示。

从表2可以看到，对数据集Letter, Pen, Optdigits, Image-Segmentation, Landsat-Satellite以及Wine，基于BP神经网络的自适应伪最近邻分类的分类性能明显好于传统的近邻分类以及伪最近邻分类。而在数据集Thyroid上，BPANN也取得了较好的分类效果。对于数据集Iris和Glass，最终的分类效果没有得到明显改善，这是由于它们属于小样本数据集，先前没有分出训练集和测试集。而BPANN分类算法在分类器设计阶段，是通过5倍交叉验证来选择训练集与测试集，交叉分组的训练数据每次的变化会对权值优化产生较大影响，进而影响分类结果。并且该算法在小样本数据集上的误差率是5次分类结果的平均值，避免了实验结果由于训练集与测试集选择的随机性引起的偶然性。

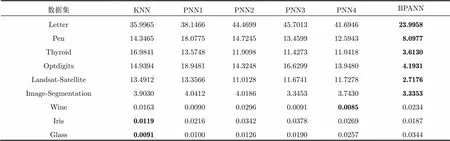
表3为表2中几种算法取得相应分类结果的分类时间(因为KNN直接计算测试样本与训练样本之间的距离，不需要进行训练，因此实验中记录的是各个算法的测试时间，即分类时间)，表中时间单位均为秒，几种分类算法分别在每个数据集上最少的分类时间用黑体表示。

表1所使用数据集的一些特征

仿真所使用的数据集特征维数样本数类数误差估计 Letter1616000个训练样本26测试样本4000个 Pen167494个训练样本10测试样本3498个 Thyroid213772个训练样本 3测试样本3428个 Optdigits643823个训练样本10测试样本1797个 Landsat-Satellite364435个训练样本 3测试样本2000个 Image-Segmentation19210个训练样本 7测试样本2100个 Iris 4150 35CV Glass 9214 65CV Wine13178 35CV

表2在9个数据集上的分类误差(%)

数据集KNNPNN1PNN2PNN3PNN4BPANN Letter4.12 k=3 3.80 3.75 4.30 3.93 3.67 Pen2.12 k=4 1.94 2.26 2.26 1.97 1.92 Thyroid6.33 k=5 6.65 6.42 8.02 6.42 6.33 Optdigits2.00 k=1 1.67 1.84 2.00 1.67 1.56 Landsat-Satellite10.6010.5510.3510.55 9.90 8.90 Image-Segmentation12.3312.3312.3312.3312.3312.14 Wine30.7228.5727.4728.6028.0125.73 Iris 2.67 2.67 2.67 3.33 2.67 3.33 Glass35.0537.1737.6137.2036.2835.27 平均误差率11.7711.7111.6312.3611.3810.98

表3 不同算法在各数据集上的分类时间(s)

数据集KNNPNN1PNN2PNN3PNN4BPANN Letter35.996538.146644.469945.701341.694623.9958 Pen14.346518.077514.724513.459912.5943 8.0977 Thyroid16.984113.574811.909811.427311.0418 3.6130 Optdigits14.939418.948114.324816.629913.9480 4.1931 Landsat-Satellite13.491213.356611.012811.674111.7278 2.7176 Image-Segmentation 3.9030 4.0412 4.0186 3.3453 3.7430 3.3353 Wine 0.0163 0.0090 0.0296 0.0091 0.0085 0.0234 Iris 0.0119 0.0216 0.0342 0.0378 0.0269 0.0187 Glass 0.0091 0.0100 0.0126 0.0190 0.0257 0.0344

由表3可得，BPANN算法在数据集Letter, Pen, Thyroid, Optdigits, Landsat-Satellite以及Image- Segmentation上的分类时间明显的小于PNN以及KNN，从算法原理可对此作出解释，PNN是通过计算距离加权和来分类，而 BPANN是由神经网络输入与输出间的映射来调节权值并分类，使得分类时间相对较少。对于小样本数据集Wine, Iris和Glass, BPANN在分类时间上没有取得明显改善，这是由于为了避免实验的偶然性，其分类时间计算的是交叉验证次数的平均值。

5 结论

针对PNN算法中距离加权系数的确定问题，本文提出了一种新的伪最近邻方法：基于BP神经网络的自适应伪最近邻分类方法。在该分类方法中，BP神经网络的输入不是待分类样本点的特征值，而是待分类样本在每一类样本集中的各个近邻的距离值，同时距离加权值不需要人为确定，而是由BP神经网络输入和输出之间的映射自适应确定，并且对每一个数据集自适应的设计其相应分类器。因此在整个分类过程中进一步减少了主观因素的参与成分，这使得分类器性能具有更好的稳定性和推广性。在多个UCI数据集上的实验结果表明，该算法与传统的KNN算法以及PNN算法相比，取得了更好的分类性能。

[1] WU Xindong, KUMAR V, QUINLAN J R,Top 10 algorithms in data mining[J]., 2008, 14(1): 1-37. doi: 10.1007/s10115-007-0114-2.

[2] MATEI O, POP P C, and VĂLEAN H. Optical character recognition in real environments using neural networks and k-nearest neighbor[J]., 2013, 39(4): 739-748. doi: 10.1107/s10489-013-0456-2.

[3] WAN C H, LEE L H, RAJKUMAR R,. A hybrid text classification approach with low dependency on parameter by integrating-nearest neighbor and support vector machine[J]., 2012, 39(15): 11880-11888. doi: 10.1016/j.eswa.2012.02.068.

[4] CARAWAY N M, MCCREIGHT J L, and RAJAGOPALAN B.Multisite stochastic weather generation using cluster analysis and k-nearest neighbor time series resampling[J]., 2014, 508: 197-213. doi: 10.1016/ j.jhydrol.2013.10.054.

[5] RAHMAN S A, HUANG Y, CLAASSEN J,Combining Fourier and lagged-nearest neighbor imputation for biomedical time series data[J]., 2015, 58: 198-207. doi: 10.1016/j.jbi.2015.10. 004.

[6] GONZÁLEZ Mabel, BERGMEIR Christoph, TRIGUERO Isaac,. On the stopping criteria for-Nearest Neighbor in positive unlabeled time series classification problems[J]., 2016, 328: 42-59. doi: 10.1016/j.ins. 2015.07.061.

[7] WANG A, AN N, CHEN G,. Accelerating wrapper- based feature selection with-nearest-neighbor[J]., 2015, 83: 81-91.doi: 10.1016/ j.knosys.2015.03.009.

[8] CHEN C H, HUANG W T, Tan T H,. Using K-nearest neighbor classification to diagnose abnormal lung sounds[J]., 2015, 15(6): 13132-13158. doi: 10.3390/s150613132.

[9] HAN Y, PARK K, HONG J,. Distance-constraint k-nearest neighbor searching in mobile sensor networks[J]., 2015, 15(8): 18209-18228.doi: 10.3390/s150818209.

[11] CHOI Sangil, YOUN Ik-hyun, LEMAY Richelle,.Biometric gait recognition based on wireless acceleration sensor using-nearest neighbor classification[C]. 2014 IEEE International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, 2014: 1091-1095.doi: 10.1109/ICCNC.2014.6785491.

[12] DUDANI S A. The distance-weighted-nearest-neighbor rule[J].,,, 1976, 6(4): 325-327. doi: 10. 1109/TSMC. 1976.5408784.

[13] GOU Jianping, XIONG Taisong, and KUANG Yin. A novel weighted voting for k-nearest neighbor rule[J]., 2011, 6(5): 833-840. doi: 10.4304/jcp.6.5.833- 840.

[14] GOU Jianping, DU Lan, ZHANG Yuhong,A new distance-weighted-nearest neighbor classier[J].&, 2012, 9(6): 1429-1436.

[15] BAILY T and JAIN A K. A note on distance-weighted- nearest neighbor rules[J].,,, 1978, 8(4): 311-313. doi: 10.1109/ TSMC.1978.4309958.

[16] MORIN R L and RAESIDE B E. A reappraisal of distance- weighted-nearest-neighbor classification for pattern recognition with missing data[J].,,, 1981, 11(3): 241-243. doi: 10.1109/TSMC.1981.4308660.

[17] ZENG Yong, YANG Yupu, and ZHAO Liang. Pseudo nearest neighbor rule for pattern classification[J]., 2009, 36: 3587-3595. doi: 10.1016/j.eswa. 2008.02.003.

[18] 杨凡, 赵建民, 朱信忠. 一种基于BP神经网络的车牌字符分类识别方法[J]. 计算机科学, 2005, 32(8): 192-195.

YANG Fan, ZHAO Jianmin, and ZHU Xinzhong. A new method of license plate characters classified recognition based on BP neural networks[J]., 2005, 32(8): 192-195.

[19] BACHE K and LICHMAN M.UCI repository of machine learning databases[OL].http://www.ics.uci.edu/~mlearn/ MLRepository.html. 2014.

Adaptive Pseudo Nearest Neighbor Classification Based on BP Neural Network

ZENG Yong SHU Huan HU Jiangping GE Yueyue

(,,611731,)

Distance-weighted coefficients between unlabeled sample point and its nearest neighbors belonging to same sample set are determined subjectively in the Pseudo Nearest Neighbor (PNN) classification algorithm, which makes it difficult to obtain optimal distance-weighted value. In this paper, an adaptive pseudo neighbor classification algorithm based on BP neural network is proposed. Firstly, the distance-weighted values between unlabeled sample point and its neighbors lying in the same sample set are regarded as the input of BP neural network. Secondly, the corresponding distance-weighted values are adaptively determined according to the mapping between the inputs and outputs of BP neural network. Finally, the classification of unlabeled sample point is judged by the outputs of BP neural network. Experimental results show that the proposed approach adaptively adjusts the distance-weighted coefficients. Moreover, the classification accuracy can be effectively improved.

Pseudo Nearest Neighbor (PNN) classification; BP neural network; Adaptive

TP181

A

1009-5896(2016)11-2774-06

10.11999/JEIT160133

2016-01-29；改回日期：2016-06-17；

2016-09-08

舒欢 shuhuan163@163.com

国家自然科学基金(61104104, 61473061)，四川省信号与信息重点实验室基金(SZJJ2009-002)

The National Natural Science Foundation of China (61104104, 61473061), The Fund of Sichuan Provincial Key Laboratory of Signal and Information Processing (SZJJ2009-002)

曾 勇： 男，1968年生，博士，副教授，研究方向为智能信息处理、智能控制理论与应用、计算机视觉与模式识别.

舒 欢： 女，1991年生，硕士生，研究方向为模式识别.

胡江平： 男，1977年生，教授，博士生导师，研究方向为多智能系统建模与控制、传感器网络信息融合、智能飞行控制等.