基于交叉点数据和三维非参数模型的雷达高度计海况偏差估计方法

蒋茂飞 许 可 刘亚龙 王 磊



基于交叉点数据和三维非参数模型的雷达高度计海况偏差估计方法

蒋茂飞①②③许 可*①②刘亚龙④王 磊①②

①(中国科学院微波遥感技术重点实验室 北京 100190)②(中国科学院国家空间科学中心 北京 100190)③(中国科学院大学 北京 100049)④(国家海洋局烟台海洋环境监测中心站 烟台 264000)

海况偏差(Sea State Bias, SSB)是雷达高度计测量海面高度的重要误差源。目前，业务化运行的雷达高度计的海况偏差校正都是采用基于风速()和有效波高(SWH)的2维经验模型方法，其海况偏差校正不确定度约为2 cm。该文提出一种基于交叉点数据和3维非参数模型的海况偏差估计方法，该方法利用星下交叉点数据，采用基于, SWH以及平均波周期(MWP)的3维非参数模型进行海况偏差估计。该文利用这种估计方法对Jason-2卫星雷达高度计2009~2011年3年的数据进行了处理，将处理结果与Jason-2卫星高度计的地球物理数据集(Geophysical Data Records, GDR)中的海况偏差校正项进行对比，结果表明该文提出的海况偏差估计方法平均能降低1.64 cm2的交叉点海面高度不符值的方差和0.92 cm2的沿轨海面高度异常值的方差，分别对应于1.28 cm和0.96 cm的均方根(RMS)海面高度，这对于提高高度计数据产品的精度具有重要意义。

雷达高度计；海况偏差；交叉点；3维非参量模型

1 引言

全球海平面上升已经越来越引起人们的关注，雷达高度计的一个主要应用就是测量平均海面高度。然而，由于海面是非高斯分布的，波谷的曲率半径比波峰大，所以波谷能反射更多的电磁能量，从而使得高度计测得的平均海面低于真实的平均海面，这种效应称为电磁偏差[4]。在高度计的回波跟踪算法中，通常假设海面高度的概率密度函数为高斯函数，而实际海面高度的概率密度函数是有偏斜度的，这样就会产生偏斜度偏差。电磁偏差和偏斜度偏差一起统称为海况偏差(Sea State Bias, SSB)，海况偏差的不确定度很大，能够达到2 cm[5,6]，随着精密定轨技术的发展，在Jason系列测高卫星中，海况偏差已经取代轨道误差成为雷达高度计测高最大的误差源[6, 7]。

在文献[15,16]的基础上，本文提出了一种基于交叉点数据和3维非参数模型的海况偏差估计方法。本文利用非线性海浪理论简单分析了波周期和海况偏差的大致关系，为将波周期信息引入海况偏差估计提供了理论依据。利用本文方法分别对Jason-2卫星雷达高度计2009~2011年3年的数据进行了处理，并将处理结果与Jason-2卫星高度计的GDR产品中的海况偏差校正项进行对比，结果表明本文提出的海况偏差估计方法能极大地降低交叉点海面高度不符值的方差和沿轨海面高度异常值的方差，这对于提高雷达高度计的测高精度具有重要意义。

2 波周期与海况偏差的关系

文献[15,16]曾将平均波周期引入海况偏差估计中，但是国内外还没有公开资料论述波周期与海况偏差的关系，本文希望通过海浪理论将波周期与海况偏差联系起来，从而为将波周期信息引入海况偏差估计提供理论依据。海况偏差主要是由海面的非线性特性所引起的，所以可以使用非线性海浪理论来进行研究。常用的非线性海浪理论主要有斯托克斯(Stokes)波理论、椭圆余弦(Cnoidal)波理论和孤立(Solitary)波理论，椭圆余弦波理论、孤立波理论以及五阶Stokes波理论都主要适用于浅水，而高度计的绝大部分有效测量点都在深水区，所以本文使用四阶Stokes波理论。

根据四阶Stokes波理论，波面轮廓可以表示为[18]

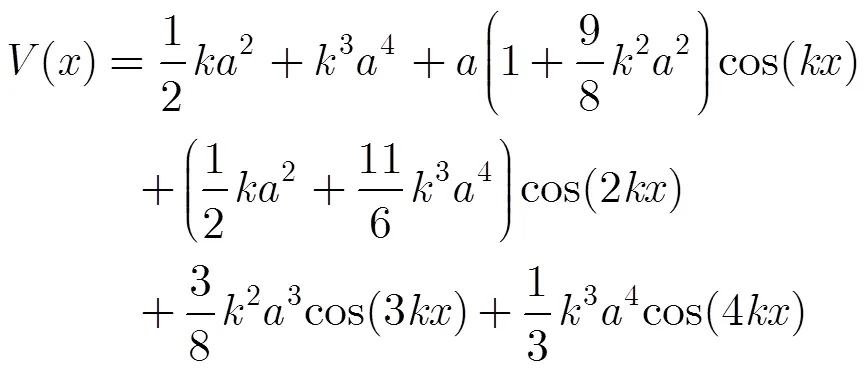
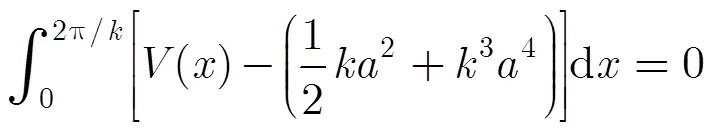
波峰到坐标原点的距离为

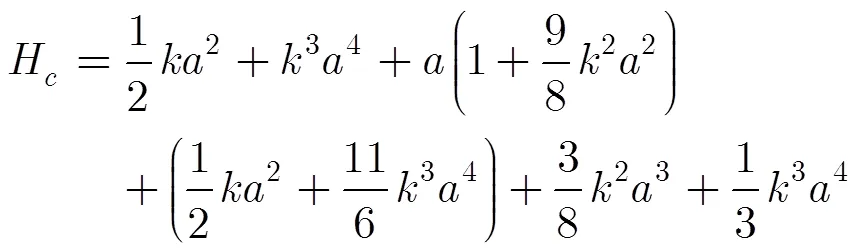
波谷到坐标原点的距离为

半波面高度到原点的距离为

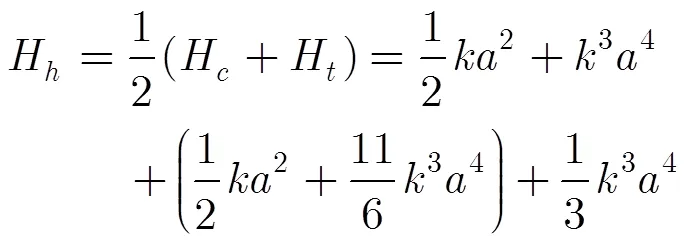
半波面高度到静止水面的距离为

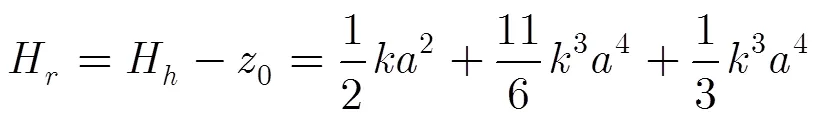
式(6)表明水面质点的振动中心不在静止水面上，而是高于静止水面，高出静止水面的距离约为,可以看作是高度计测得的平均海面，可以看作是真实的平均海面，也就是高度计测得的平均海面会低于实际的平均海面，而真实的平均海面与高度计测得的平均海面之差就可以看作是电磁偏差，所以也可以看作是四阶Stokes波理论得到的电磁偏差。

图1(a)给出了当波周期固定为9 s时，随波高的变化关系，当波周期固定时，随波高的增大而增大；图1(b)给出了当波高固定为2.5 m时，随波周期的变化关系，当波高固定时，随波周期的增大而减小。而电磁偏差是海况偏差的最主要成分，所以图1也可以大致反映海况偏差与波长和波周期的关系。

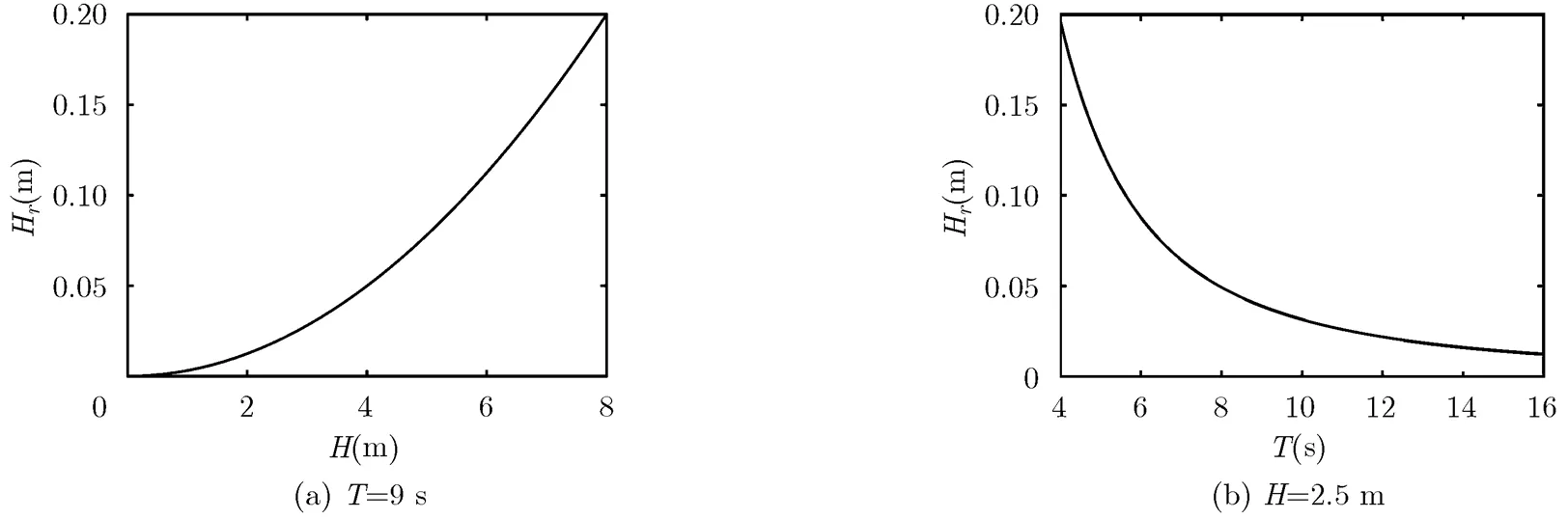
图1 四阶Stokes波理论得到的电磁偏差Hr随波高H和波周期T的变化

以上提到的波浪是具有固定波高、周期的单一波浪，其波面形状是规则的，然而实际海面上的波浪都是不规则的，由不同波高和周期的单一波浪叠加而成。所以，在利用经验模型来估计海况偏差时，我们使用有效波高和平均波周期。

3 已有的3维非参数海况偏差模型

3.1 3维非参数回归模型

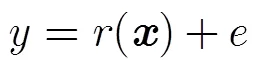
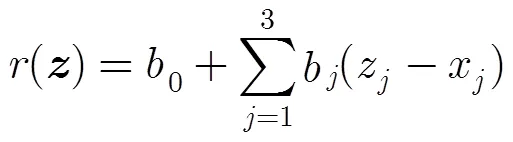
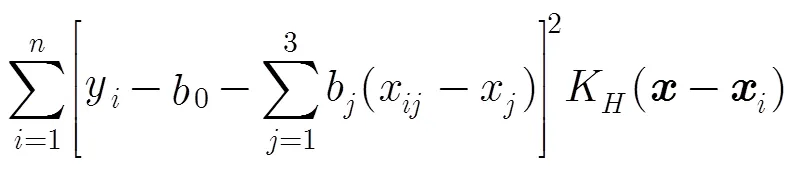
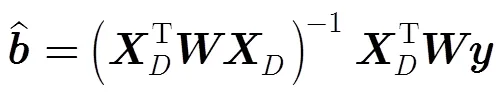
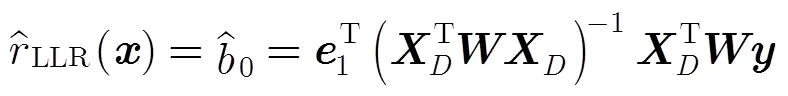
3.2 文献[15,16]的3维非参数海况偏差模型

传统的非参数海况偏差模型主要是利用和SWH作为模型输入的2维经验模型，文献[15,16]在2010年提出的3维非参数海况偏差模型采用, SWH和MWP作为模型的输入[16]。如何提取SSB信息是建立SSB模型的关键，TRAN等人将未经SSB校正的瞬时海面高度减去通过平均海面模型得到的平均海面高度，从而得到未经SSB校正的海面高度异常值并从中提取SSB信息。

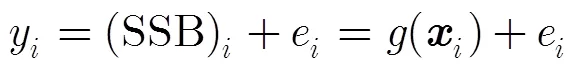
这样就得到了式(7)中典型的回归模型的表达式，给定组观测值，通过式(11)就可以得到任意所对应的SSB估计值。

4 基于交叉点数据的3维非参数海况偏差估计

4.1 基于交叉点数据的3维非参数海况偏差估计方法

与文献[15,16]提取SSB信息的方法不同，本文从未经SSB校正的交叉点海面高度不符值中提取SSB信息。具体思路如下[7,12]：

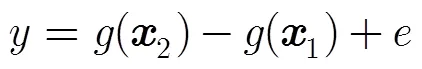
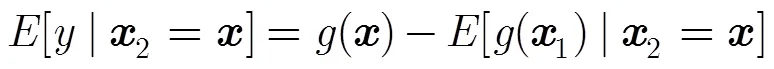
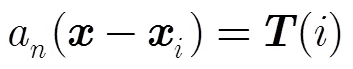
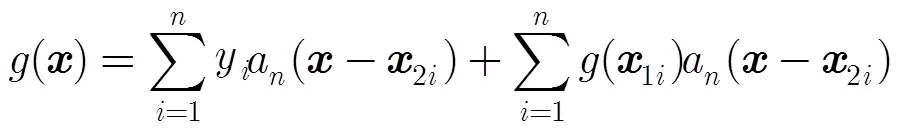
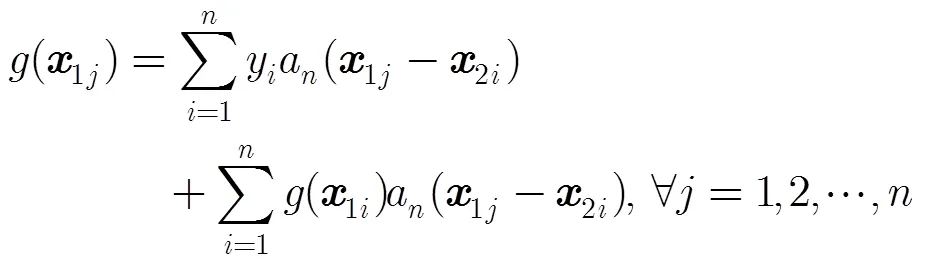
转化为矩阵的形式可以得到

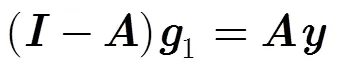
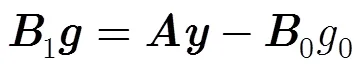
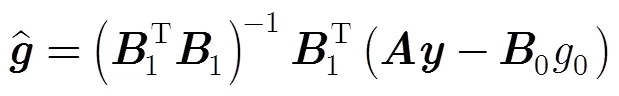
4.2 两种3维非参数海况偏差估计方法的比较

利用海面高度异常数据估计SSB和利用交叉点数据估计SSB的主要区别是获取SSB信息的方式不同，前者是从海面高度异常值中获取SSB信息，而后者是从交叉点的海面高度不符值中获取SSB信息。与利用海面高度异常数据估计SSB的方法相比，利用交叉点数据估计SSB的方法具有以下优势：

(1)海面高度异常值是高度计测得的瞬时海面高度与通过平均海面模型计算得到的平均海面高度之差，对于同一个平均海面模型，在某一个位置，平均海面高度是固定的，其中高度计的系统误差会影响SSB的测量结果，由于高度计的系统误差在交叉点数据获取过程中是不变的，通过在交叉点处将升轨和降轨的海面高度做差就可以消除这样的误差。

(2)计算海面高度异常值需要用到平均海面模型，平均海面模型是通过多个高度计多年测高数据平均得到，不同高度计所采用的数据处理方法有差异，所用到的误差校正方法也不一样，这些都会引入误差。同时，利用不同平均海面模型得到的SSB估计值也相差很大[14]；而利用交叉点的方法则没有这一问题。

5 Jason2卫星高度计海况偏差估计

5.1 交叉点数据处理

本文使用的平均波周期来自于欧洲中期天气预报中心(European Centre for Medium-range Weather Forecasts, ECMWF)再分析数据集ERA- Interim, ERA-Interim是ECMWF的第3代全球再分析数据产品，提供了自1979年以来的再分析资料，并实时更新。ERA-Interim提供每天4个时刻的数据，分别在00:00, 06:00, 12:00和18:00 UTC，数据以网格的形式提供，本文使用数据的网格分辨率为。ERA-Interim只提供每天4个时刻的数据，所以需要将数据在空间和时间上插值到高度计测量点处。本文采用先在空间上双线性插值，再在时间上线性插值的方法。本文用到的风速、有效波高以及计算海面高度所需要的数据都来源于Jason-2卫星经过完全定标的D版本的GDR数据。Jason-2卫星于2008年6月发射，它是TOPEX/ POSEIDON, Jason-1测高卫星的后继星，被公认为目前测高精度最高的卫星。

利用交叉点数据和3维非参数模型估计SSB时需要用到风速、有效波高、平均波周期和交叉点处未经SSB校正的海面高度不符值，需要把它们插值到交叉点处。本文采用三次样条插值的方法，只有在交叉点两侧各有4个连续的测量点时得到的交叉点才有效，这样可以保证较好的高度计数据质量。

5.2 Jason-2海况偏差估计过程

在利用非参数估计方法估计SSB时，需要建立一个关于, SWH和MWP的3维查找表，图2给出了, SWH和MWP的分布直方图，图中的结果是利用2011年全年的数据统计得到的。在本文所采用的查找表中，, SWH和MWP的取值范围分别为：0~30 m/s, 0~12 m和0~18 s。在利用2维非参数模型估计SSB时，在得到后，需要整体减去，使得，即平坦无风的海面的海况偏差为零。在利用3维非参数模型估计SSB时，在得到后，本文采用将整体减去的方法得到最终的SSB估计值的查找表，选择MWP=9 s是因为MWP的平均值在9 s附近。利用交叉点数据和3维非参数模型估计SSB的步骤如下：

步骤 1 对单个周期(Cycle)的交叉点数据，假设一个,可以是任意一个合理的值，例如。

步骤 4 对每个Cycle的交叉点数据重复步骤1，步骤2，步骤3，再对所有Cycle得到的结果取平均得到。

步骤6 在得到3维SSB查找表后，根据沿轨任意一个测量点的, SWH和MWP，通过插值的方法得到该测量点的SSB估计值。

5.3 Jason-2海况偏差估计结果

分别使用了2009, 2010和2011年3年的交叉点数据和3维非参数模型得到SSB估计值(CR3D)，因为利用不同年份数据得到的SSB估计值相差不大，在数据密集区都在1 cm以下，这里仅以利用2011年的数据得到的SSB估计值的查找表作为参考。为了更好地表示结果，固定第3个输入参量，以2维网格的形式给出SSB估计值在各个平面的等值线分布，如图3所示，等值线的单位为cm，3个固定值分别选在, SWH, MWP的平均值附近，这样可以保证在相应的平面有较多的测量点，3个固定值分别为：MWP=9 s,=7.5 m/s, SWH=2.5 m。图中阴影部分为测量点个数小于20的区域，代表数据稀疏区域，而图中白色部分代表数据密集区域，统计数据来源于2011年全年的数据，我们主要关心的是数据密集区域。

图3(a)是在MWP等于9 s时，SSB估计值在(, SWH)平面的分布图，当MWP固定时，和相比，SSB随SWH的变化更为明显，在给定的条件下，SSB的幅值是SWH的递增函数，这和传统的利用基于和SWH的2维非参数模型得到的结果[5,12,14]是一致的，也和图1(a)的结果吻合。图3(b)是当等于7.5 m/s时，SSB估计值在(MWP, SWH)平面的分布图，当和SWH固定时，SSB会随着MWP变化，MWP越大，SSB的幅值越小。高度计的绝大部分有效测量点都在深水区，而在深水区，影响海面非线性的主要是波陡，在波高一定时，波周期越大，波陡越小，海面非线性越弱，海况偏差也就越小，所以得到的结果是合理的，也和图1(b)的结果吻合。在数据密集区域，对于给定的SWH，随着MWP的变化，SSB有约3~4 cm的变化。图3(c)给出了当SWH等于2.5 m时，SSB估计值在(, MWP)平面的分布图，在数据密集区域，当SWH固定时，SSB随MWP的变化比随的变化更为明显，这表明MWP对SSB的影响比对SSB的影响大，在其它条件都相同时，MWP越大，SSB的幅值越小。

图2 风速U、有效波高SWH和平均波周期MWP的分布直方图

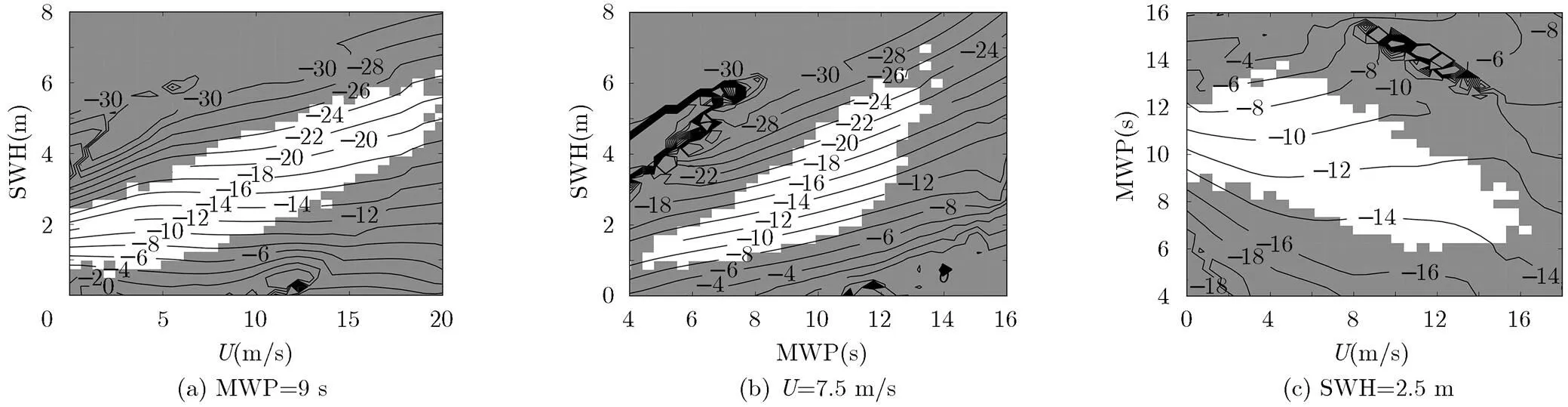
图3 利用CR3D得到的Jason-2 SSB估计值(cm)在各平面的分布

Jason-2的GDR产品中含有SSB校正项，本文将利用交叉点数据和3维非参数模型得到的SSB估计值(CR3D)和Jason-2的GDR产品中SSB校正项(JA2GDR)作比较，以此来评估利用本文所提出的SSB估计方法得到的SSB估计值。由于目前还不能直接利用卫星高度计自身测得的数据得到海况偏差的精度，所以通常是通过海况偏差校正对整个测高系统的贡献来评估SSB估计值。

海面高度不符值是最主要的用于分析整个测高系统性能的工具，通过海面高度不符值可以分析升轨和降轨的海面高度(Sea Surface Height, SSH)在交叉点处的一致性。在理想的条件下，交叉点海面高度不符值应该为零，但是由于轨道误差、地球物理校正误差和海洋波动等因素的影响，交叉点海面高度不符值通常不为零。交叉点海面高度不符值的方差可以估计整个测高系统的表现，其值越小，表明测高系统的整体表现越好[19,20]。从表1可以看出，和Jason-2的GDR中的SSB校正项相比，在其它条件都相同时，CR3D可以将海面高度不符值的方差降低1.54~1.75 cm2, 平均降低了1.64 cm2，对应于1.28 cm的均方根(RMS)海面高度。

沿轨海面高度异常(Sea Level Anomalies, SLA)也是估计测高系统整体表现的一个重要工具，沿轨SLA是通过沿轨的瞬时海面高度减去相应的平均海面得到，本文所用到的平均海面由CLS2011平均海面模型得到。沿轨SLA的方差可以用来监测测高系统的长期稳定性，其值越小表明测高系统的整体性能越好[19,20]。从表1可以看出，和Jason-2的GDR中的SSB校正项相比，在其它条件都相同时，CR3D可以将沿轨SLA的方差降低0.71~1.10 cm2，平均降低了0.92 cm2，对应于0.96 cm的均方根(RMS)海面高度。

综上所述，和Jason-2中的SSB校正项相比，CR3D可以大幅降低海面高度不符值的方差和沿轨SLA的方差，这表明CR3D可以大幅提高雷达高度计的测高精度。

文献[15,16]的3维SSB模型是通过海面高度异常数据得到的，为了将利用本文方法得到的SSB估计值和利用文献[15,16]的3维SSB模型得到的SSB估计值进行比较，本文利用2010年的海面高度异常数据建立了一个3维SSB模型，并使用该模型得到了相应的SSB估计值(SLA3D)。图4给出了相对海面高度不符值的方差，它是通过分别利用CR3D和SLA3D进行SSB校正后得到的海面高度不符值的方差减去利用JA2GDR进行SSB校正后的海面高度不符值的方差得到。图5给出了相对沿轨SLA方差，它是通过分别利用CR3D和SLA3D进行SSB校正后得到的沿轨SLA方差减去利用JA2GDR进行SSB校正后的沿轨SLA方差得到。图4和图5的结果都是利用2011年(Cycle 93-Cycle 127)的数据通过每个Cycle单独计算得到。从图4和图5可以看出，和JA2GDR相比，CR3D和SLA3D都可以降低交叉点海面高度不符值的方差和沿轨SLA的方差。而和SLA3D相比，利用CR3D得到的交叉点海面高度不符值的方差和沿轨SLA的方差都更小，这也表明CR3D比SLA3D有更好的性能。

表1利用交叉点数据和3维非参数模型得到的SSB估计值与Jason-2的GDR中的SSB校正项的比较

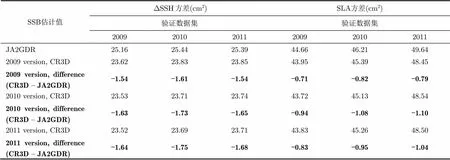
SSB估计值方差(cm2)SLA方差(cm2) 验证数据集验证数据集 200920102011200920102011 JA2GDR25.1625.4425.3944.6646.2149.64 2009 version, CR3D23.6223.8323.8543.9545.3948.45 2009 version, difference (CR3D – JA2GDR)-1.54-1.61-1.54-0.71-0.82-0.79 2010 version, CR3D23.5323.7123.7443.7245.1348.54 2010 version, difference (CR3D – JA2GDR)-1.63-1.73-1.65-0.94-1.08-1.10 2011 version, CR3D23.5223.6923.7143.8345.2648.50 2011 version, difference (CR3D – JA2GDR)-1.64-1.75-1.68-0.83-0.95-1.04

注：表中方差表示交叉点海面高度不符值的方差，第1栏中的“JA2GDR”表示Jason-2的GDR产品中的SSB校正项，“2009 version, CR3D”表示利用2009年的交叉点数据和3维非参数模型得到的SSB估计值，“2009 version, difference (CR3D – JA2GDR)” 所在的行表示相对于Jason-2的GDR产品中SSB校正项，利用2009年的交叉点数据和3维非参数模型得到的SSB估计值所计算得到的或SLA的方差的减少量。

6 结论

海况偏差由于其较大的不确定度已经成为雷达高度计测量海面高度最大的误差来源。传统的海况偏差校正采用以高度计测得的风速和有效波高为输入参量的2维经验模型，本文从非线性海浪理论的角度简单分析了波周期和海况偏差的大致关系，并联合ECMWF再分析数据集提供的平均波周期以及高度计测得的风速和有效波高，提出了一种利用交叉点数据和3维非参数模型估计海况偏差的方法。利用Jason-2卫星雷达高度计2009~2011年3年的数据对得到的SSB估计值进行评估，和Jason-2的GDR产品中的SSB校正项相比，利用本文方法所得到的SSB估计值能将交叉点海面高度不符值的方差和沿轨SLA方差分别降低1.64 cm2和0.92 cm2，分别对应于1.28 cm和0.96 cm的均方根(RMS)海面高度。而和现有的利用海面高度异常数据得到的3维SSB模型相比，利用本文方法所得到的3维SSB模型也具有更好的表现。由于ECMWF的再分析数据已经被广泛应用于业务化雷达高度计二级数据处理，所以本文提出的海况偏差估计方法具有较强的实用性。

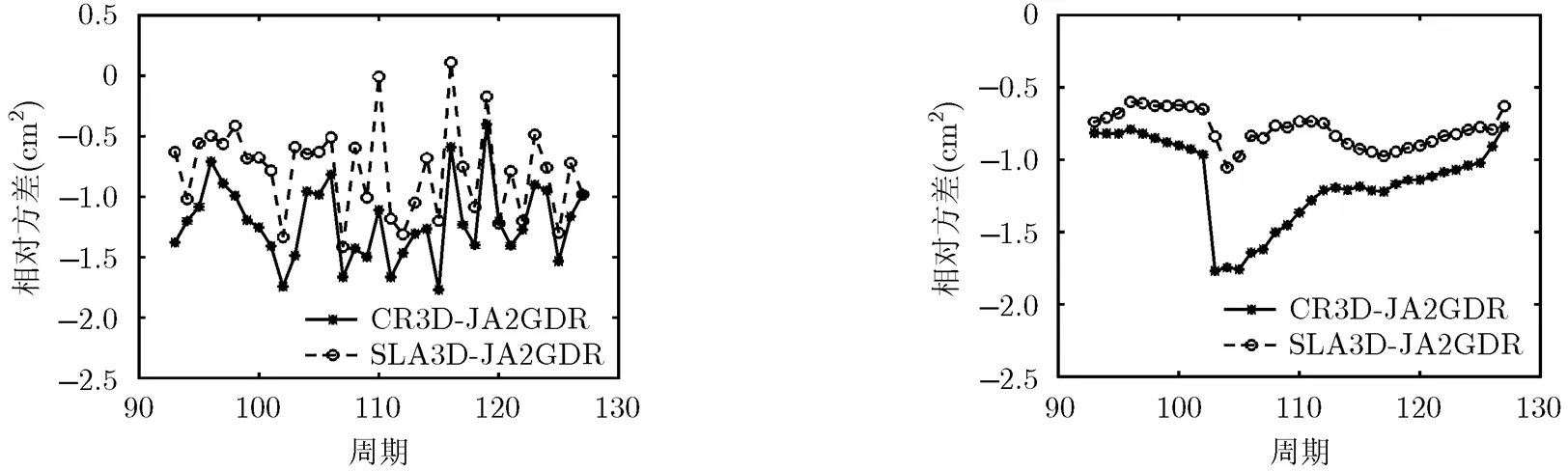
图4 高度不符值相对方差(CR3D和SLA3D得到的海面高度     图5 沿轨SLA相对方差(CR3D和SLA3D得到的

不符值的方差–JA2GDR得到的海面高度不符值的方差)     SLA的方差–JA2GDR得到的SLA的方差)

[1] 万珺之. 基于有源定标器的海洋二号高度计系统延迟在轨绝对定标研究[D]. [博士论文], 中国科学院国家空间科学中心, 2015.

WAN J Z. Study on HY-2 altimeter system delay in-orbit absolute calibration using reconstructive transponder [D]. [Ph.D. dissertation], National Space Science Center, Chinese Academy of Sciences, 2015.

[2] 王磊. 高精度卫星雷达高度计数据处理技术研究[D]. [博士论文], 中国科学院国家空间科学中心, 2015.

WANG L. Study on the data processing for high precision satellite radar altimeter[D]. [Ph.D. dissertation], National Space Science Center, Chinese Academy of Sciences, 2015.

[3] 王磊, 许可, 史灵卫, 等. 一种消除合成孔径雷达高度计延迟校正中残余误差的新算法及仿真验证[J]电子与信息学报, 2015, 37(11): 2713-2718. doi: 10.11999/JEIT150282.

WANG L, XU K, SHI L W,. A new range migration correction algorithm and its simulation for SAR altimeter[J].&, 2015, 37(11): 2713-2718. doi: 10.11999/JEIT150282.

[4] GHAVIDEL A, SCHIAVULLI D, and CAMPS A. Numerical computation of the electromagnetic bias in GNSS-R altimetry[J]., 2016, 54(1): 489-498. doi: 10.1109/TGRS.2015. 2460212.

[5] GASPAR P and FLORENS J P. Estimation of the sea state bias in radar altimeter measurements of sea level: Results from a new nonparametric method[J].-, 1998, 103(C08): 15803-15814. doi: 10. 1029/98JC01194.

[6] DUMONT J P, ROSMORDUC V, PICOT N,. OSTM/ Jason-2 products book[R]. 2011.

[7] GHAVIDEL A and CAMPS A. Time-domain statistics of the electromagnetic bias in GNSS-reflectometry[J]., 2015, 7(1): 11151-11162. doi: 10.3390/rs70911151.

[8] MILLET F W, WARNICK K F, NAGEL J R,. Physical optics-based electromagnetic bias theory with surface height-slope cross-correlation and hydrodynamic modulation [J]., 2006, 44(6): 1470-1483. doi: 10.1109/TGRS.2005.863852.

[9] ELFOUHAILY T, THOMPSON D R, CHAPRON D,. Improved electromagnetic bias theory[J]., 2000, 105(C1): 1299-1310. doi: 10.1029/1999JC900277.

[10] ELFOUHAILY T, THOMPSON D R, CHAPRON D,. Improved electromagnetic bias theory: Inclusion of hydrodynamic modulations[J].-, 2001, 106(C3): 4655-4664. doi: 10.1029/ 1999JC000086.

[11] CHELTON D B. The sea-state bias in altimeter estimates of sea-level from collinear analysis of topex data[J]., 1994, 99(C12): 24995-25008. doi: 10.1029/94JC02113.

[12] GASPAR P, LABROUE S, OGOR F,. Improving nonparametric estimates of the sea state bias in radar altimeter measurements of sea level[J]., 2002, 19(10): 1690-1707. doi: 10.1175/1520-0426(2002)019<1690:INEOTS >2.0.CO;2.

[13] GASPAR P, OGOR F, LETRAON P Y,. Estimating the sea-state bias of the topex and poseidon altimeters from crossover differences[J].-, 1994, 99(C12): 24981-24994. doi: 10.1029/ 94JC01430.

[14] LABROUE S, GASPAR P, DORANDEU J,. Nonparametric estimates of the sea state bias for the Jason-1 radar altimeter[J]., 2004, 27(3-4): 453-481. doi: 10.1080/01490410490902089.

[15] TRAN N, VANDEMARK D, CHAPRON B,. New models for satellite altimeter sea state bias correction developed using global wave model data[J].

-, 2006, 111(C9): 141-152. doi:

10.1029/2005JC003406.

[16] TRAN N, VANDEMARK D, LABROUE S,. Sea state bias in altimeter sea level estimates determined by combining wave model and satellite data[J].-, 2010, 115(C03020): 1-7. doi: 10.1029/ 2009JC005534.

[17] 苗洪利, 王鑫, 王桂忠, 等. 改进的高度计海况偏差估计参数模型研究[J].中国海洋大学学报(自然科学版), 2015, 45(12): 119-124. doi: 10.16441/j.cnki.hdxb.20150125.

MIAO H L, WANG X, WANG G Z,. Study on the improved sea state bias parametric model[J].(), 2015, 2015, 45(12): 119-124. doi: 10.16441/j.cnki.hdxb. 20150125.

[18] 文圣常, 余宙文. 海浪理论与计算原理[M]. 北京: 科学出版社, 1984: 95-115.

WEN S H and YU Z W. Wave Theory and Calculation Principles[M]. Beijing: Science Press, 1984: 95-115.

[19] ABLAIN M, PHILIPPS S, PICOT N,. Jason-2 global statistical assessment and cross-calibration with Jason-1[J]., 2010, 33(S1): 162-185. doi: 10.1080/ 01490419.2010.487805.

[20] PRANDI P, PHILIPPS S, PIGNOT V,. SARAL/AltiKa global statistical assessment and cross-calibration with Jason-2[J]., 2015, 84(5): 297-312. doi: 10.1080/01490419.2014.995840.

A New Method for Radar Altimeter Sea State Bias Estimation Based on Crossover Data and Three-dimensional Nonparametric Model

JIANG Maofei①②③XU Ke①②LIU Yalong④WANG Lei①②

①(,,100190,)②(,,100190,)③(,100049,)④(,,264000,)

The Sea State Bias (SSB) is an important source of error in satellite altimetry. Operational SSB correction models are based on the altimeter-measured wind speed () and Significant Wave Height (SWH). This paper presents a new method to estimate the SSB from the crossover differences using a three-dimensional nonparametric model based on, SWH, and the Mean Wave Period (MWP). Evaluated by the separate annual data sets from 2009 to 2011, the SSB values estimated with the presented method can decrease the variance of the crossover Sea Surface Height (SSH) differences by 1.64 cm2, or 1.28 cm RMS, and decrease the variance of the Sea Level Anomalies (SLA) by 0.92 cm2, or 0.96 cm RMS in comparison to the SSB values in the Geophysical Data Records (GDR) of Jason-2. It is of great significance for improving the precision of altimeter products.

Radar altimeter; Sea state bias; Crossover; Three-dimensional nonparametric model

TN953

A

1009-5896(2016)11-2731-08

10.11999/JEIT160195

2016-03-03；改回日期：2016-07-12；

2016-09-30

许可 xuke@mirslab.cn

蒋茂飞： 男，1989年生，博士生，研究方向为雷达高度计数据处理.

许 可： 男，1967年生，博士，研究员，博士生导师，主要研究方向为星载雷达高度计系统技术、合成孔径雷达高度计系统技术和信号处理技术.

刘亚龙： 男，1985年生，博士，研究方向为雷达高度计数据处理.

王 磊： 男，1986年生，博士，研究方向为雷达高度计信号处理.