基于混合稀疏基字典学习的微波辐射图像重构方法
朱 路 宋 超 刘媛媛 黄志群 王 杨
基于混合稀疏基字典学习的微波辐射图像重构方法
朱 路*宋 超 刘媛媛 黄志群 王 杨
(华东交通大学信息工程学院 南昌 330013)
目前的微波辐射测量成像系统在一次观测中所采集的数据量大,基于奈奎斯特空间采样及常规微波辐射图像重构方法难以实现高分辨率要求。该文针对微波辐射干涉测量在频域中进行,采用傅里叶最优随机抽取的超稀疏干涉测量(低于奈奎斯特采样)对微波辐射图像进行线性压缩投影,降低数据采样。考虑微波辐射图像在总体差分域和小波中都具有可压缩特性,提出总体差分和小波混合正交基的K-SVD字典学习微波辐射图像重构模型,利用Bregman和交替迭代算法求解该模型,重构线性压缩投影信息从而获得微波辐射图像。仿真实验表明,该文提出的算法在微波辐射图像重构效果、噪声稳定性上优于DLMRI算法和GradDLRec算法。
微波辐射图像;超稀疏干涉测量;混合正交基字典学习;交替迭代方法
1 引言
微波辐射计是微波遥感的手段之一,它通过测量目标的微波辐射特性,反映目标内在的物理特征信息,但对目标表面粗糙度等宏观结构特征不敏感。研究表明,土壤微波辐射基本上是由土壤的复介电常数决定,水的复介电常数实部约为80左右,而干燥土壤的复介电常数为3~5,土壤的微波辐射几乎依赖于它的湿度含量(土壤湿度)。因此,利用微波辐射计获得土壤微波辐射图像的特征主要取决于土壤湿度。通过获取的微波辐射图像可以反演土壤湿度数据,进而对土壤湿度数据分析可以提高气象预报的准确度,有效监测干旱及洪涝等地质灾害。干涉测量综合孔径微波辐射计(Interferometric Synthetic Aperture Microwave Radiometry, ISAMR)[1]把小口径阵列综合成大的观测口径,不需要机械扫描可以成像,解决实孔径微波辐射计的缺点。同时,ISAMR在基于奈奎斯特空间采样的基础上,采用最小冗余阵列稀疏排列,可以减少观测天线的数量。但是,L-Band的星载ISAMR要实现50 km的空间分辨率,仍需要直径达9 m左右的天线阵列[2]。并且,随着图像向精细化和结构化方向的发展,为了获得高分辨率的微波辐射图像,需增加系统的复杂度。对此,基于奈奎斯特采样和常规微波辐射成像方法难以实现。
压缩感知(Compressed Sensing, CS)理论是近几年信息处理领域的重大突破[3],CS理论是将信号的稀疏先验信息引入到信号重构过程中,利用远小于奈奎斯特抽样率重构原始信号,从而有效降低传感器和抽样系统的复杂性。信号的稀疏表示是重构的先决条件,即信号在字典下的表示系数越稀疏则重构质量越高,选择最优字典是信号重构的关键。图像通常包含多种结构信息,如分段过平滑性、变换域的稀疏性、低秩等[4],对于复杂场景的微波辐射图像,单一的正交基难以最优稀疏表示。文献[5]提出了级联字典与OMP的图像重构方法,即利用全变差分和小波的级联字典对微波辐射图像进行稀疏表示,然后用OMP算法重构高分辨率的微波辐射图像,但该方法缺乏自适应性。K-SVD字典学习(Dictionary Learning, DL)方法[6]能够自适应稀疏表示信号,其基本思路是利用奇异值分解(Singular Value Decomposition, SVD)方式代替逆矩阵对字典中的原子进行逐个更新以减少表示误差,简化计算过程,并同步更新当前迭代原子所对应的稀疏系数以加快算法的收敛速度[6,7]。文献[8]提出了基于自适应学习稀疏字典的DLMRI算法(MR Image reconstruction by Dictionary Learning),该算法利用高度欠采样的k空间数据,在图像域中自适应学习字典,通过非线性重构算法获得较高质量的MRI。文献[9]提出GradDLRec算法(Gradient based Dictionary Learning method for image Recovery),结合TV (Total Variation)和字典学习,分别对横向差分图像和纵向差分图像进行字典训练,然后重构MRI图像;文献[10]通过在图像梯度和稀疏域中进行字典学习,训练出的字典稀疏表示能力更强,从而重构分辨率更高的MRI。文献[11-13]根据图像具有的层次化特征,提出多层字典的训练方法,该方法能够处理大尺度图像分类问题。文献[14]根据信号稀疏表示的余量具有不同的几何结构这个特征,提出多结构字典学习方法,从训练数据中提取信号的本质结构。因此,深入挖掘图像的多种结构信息训练字典是复杂场景微波辐射图像稀疏表示的有效手段。
考虑相同的稀疏采样,信号在字典下的表示系数越稀疏则重构质量越高,本文将总体差分和小波变换同时引入到信号重构模型,提出基于混合基字典学习的微波辐射图像重构方法。该方法根据微波辐射图像通常具有多种结构信息,利用傅里叶随机抽取对微波辐射图像进行稀疏采样,通过混合基字典训练学习(K-SVD)稀疏表示微波辐射图像,采用交替迭代算法(Alternating Direction Method, ADM)求解图像重构模型中的各个凸优化子问题,获得高分辨的微波辐射图像。
2 基于压缩感知的微波辐射成像模型
2.1压缩感知(Compressed Sensing, CS)理论
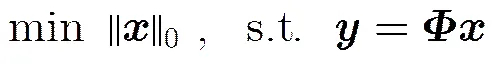
(2)
由于1范数是凸问题,可以采用内点法、梯度投影法以及同伦算法等凸优化方法求解。
2.2 微波辐射稀疏干涉测量成像模型
根据微波辐射测量和综合孔径干涉测量理论[1,15],建立微波辐射计阵列信号相关输出与谱亮度之间的关系:
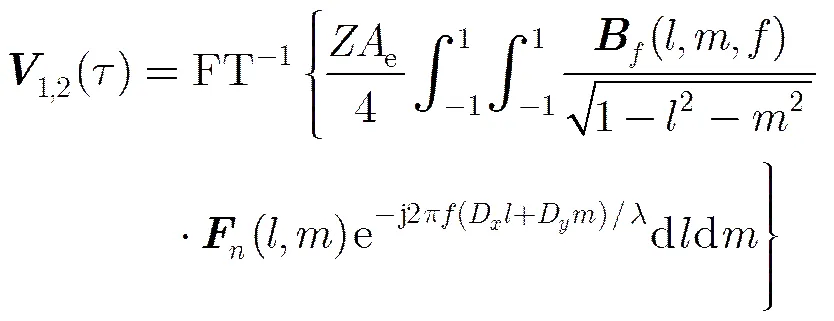
对式(3)进行简化和整理,建立微波辐射图像与理想空间干涉测量的傅里叶关系:
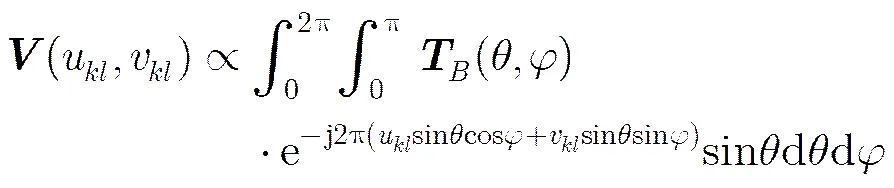
考虑微波辐射计接收机的随机噪声,对空间频率进行离散化,然后随机选择空间傅里叶频率分量,建立微波辐射离散的随机稀疏干涉测量模型:
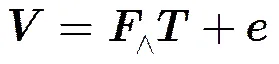
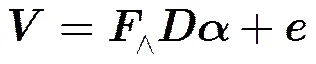
3 基于混合基字典学习的微波辐射图像重构方法
文献[5]指出微波辐射图像在总体差分和小波中都具有可压缩特性,在DLMRI算法和GradDLRec算法的基础上,本文引入TV和Daubechies (Db4)小波,建立总体差分和小波混合正交基稀疏表示的字典学习微波辐射图像重构模型:
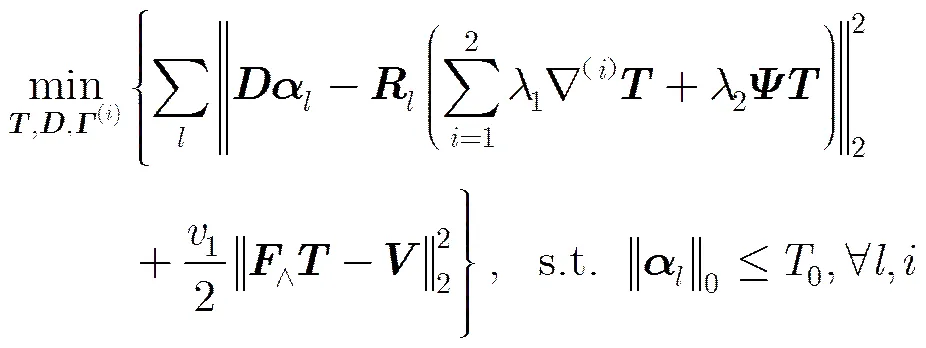
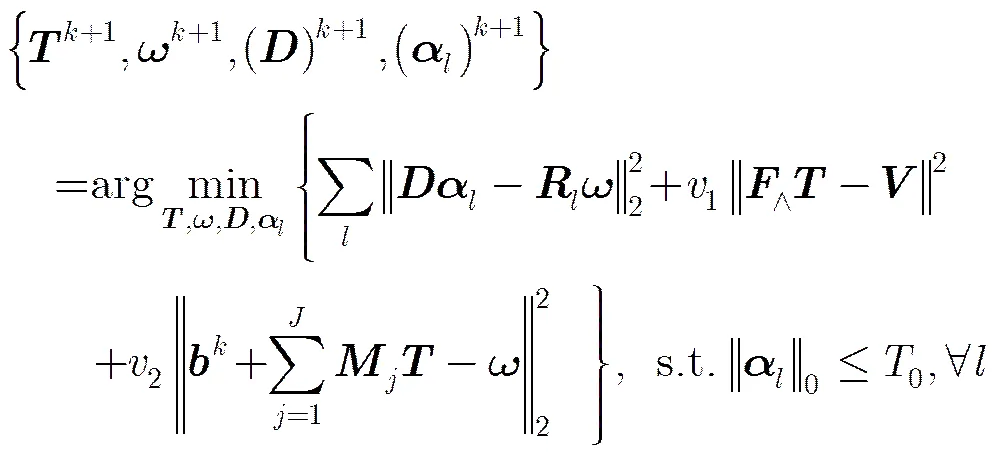
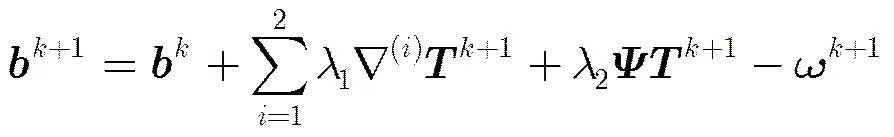
其中,2表示正惩罚参数。采用交替迭代方法(Alternating Direction Method, ADM)对式(8)进行去耦合获得P1, P2, P3 3个子问题,分别求解3个子问题可以获得式(8)的解析解。
(P1)
(P2)
(P3)
采用最小二乘法求P1问题,求导P1并令其导数为零,得
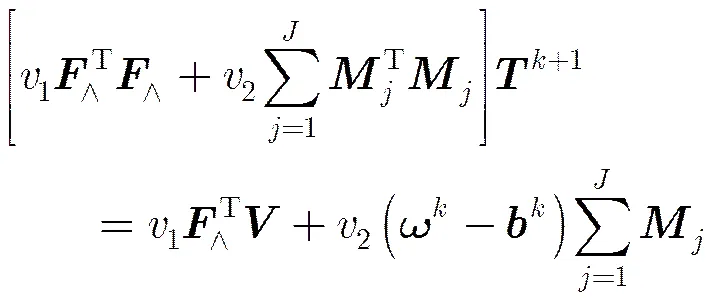

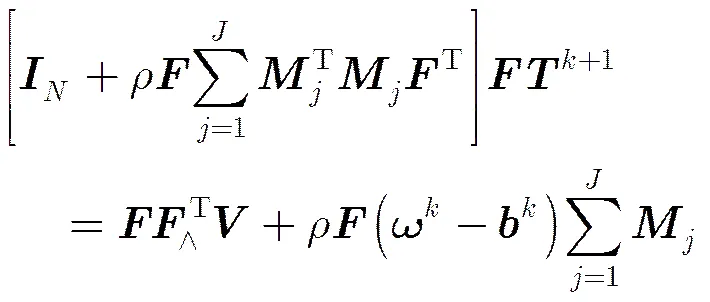

采用最小二乘法求P2问题,对其求导并令其导数为零,结果为
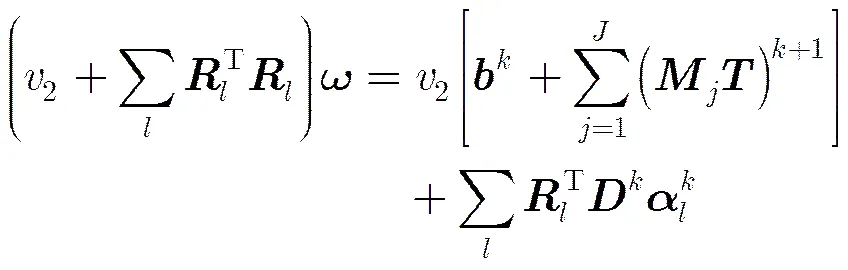
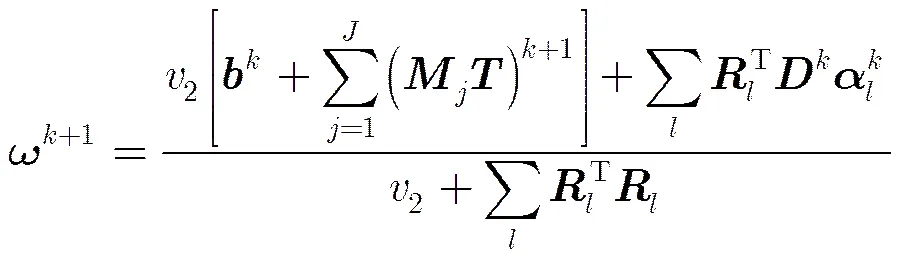
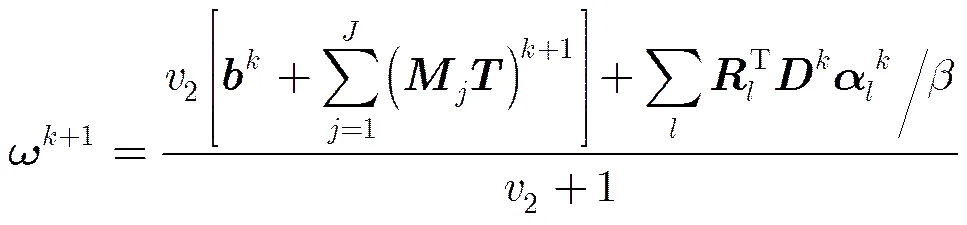

表1 本文算法的步骤
4 实验仿真及分析
这部分内容主要通过仿真实验分析本文算法的性能。考虑文献[5]采用的观测矩阵是高斯随机矩阵,微波辐射成像(MRI)和微波辐射测量通常在频域中观测,本文利用傅里叶随机抽取采样微波辐射图像。因此,本文主要与DLMRI算法、GradDLRec算法进行比较。在实验仿真中,采用如图1所示的月球微波辐射图像作为测试对象,图像大小为256×256,其频谱图如图1(b)所示。从频谱图中可以看出,低频信息主要分布在中间区域,高频信息则分布在边缘区域。根据低频信息和高频信息分布比较集中的特点,利用不同采样概率的随机傅里叶抽取对块图像进行最优观测,如图1(c)采样方式所示。该采样方式在总采样率不变的情况下,实现对采样资源的优化处理。然后分别通过DLMRI算法、GradDLRec算法和本文算法重构微波辐射图像。其中,DLMRI算法参数设置如下:图像块大小为6,稀疏字典大小==36,图像块重叠抽取步长=1,=36,=140, K-SVD字典学习算法采用10次循环迭代,200×个图像块,稀疏度0=5; GradDLRec算法参数设置同DLMRI算法,添加参数=140,=3;本文算法参数设置也同DLMRI算法,增加参数=0.5,=0.5。设置6个不同的采样率Ra=0.25, 0.35, 0.47, 0.58, 0.70, 0.85,依次仿真。其中,采样率Ra定义为采集信号的长度与实际信号的长度之比,即Ra=/。本文将对压缩采样的重构效果(PSNR, MSE)、噪声稳定性和计算复杂度进行分析。
4.1 PSNR和MSE仿真分析
PSNR为峰值信噪比(Peak Signal to Noise Ratio, PSNR),是一种常用的重构图像客观评价标准。PSNR的定义式为:PSNR=10lg((2-1)2/MSE),其中表示图像亮度的位数,MSE为均方误差。图2是在采样率为0.58的条件下,采用DLMRI算法、GradDLRec算法和本文算法重构月球微波辐射图像的仿真结果。表2,图3(a)是3种重构算法重构月球微波辐射图像的PSNR结果,表3,图3(b)是3种重构算法重构月球微波辐射图像的MSE结果。
通过分析表2,表3,图3(a)和图3(b)的仿真结果,本文算法的重构图像效果(主观视觉和客观PSNR值以及MSE值)优于DLMRI算法和GradDLRec算法,而且本文算法保留了图像的大部分细节信息,获得了更加清晰的微波辐射图像。
图4是在采样率为0.58的条件下,采用DLMRI算法、GradDLRec算法和本文算法重构地球微波辐射图像的仿真结果。表4,图5(a)是3种重构算法重构地球微波辐射图像的PSNR结果,表5,图5(b)是3种重构算法重构地球微波辐射图像的MSE结果。

图1 测试图像以及采样模式

图2 月球微波辐射重构图像
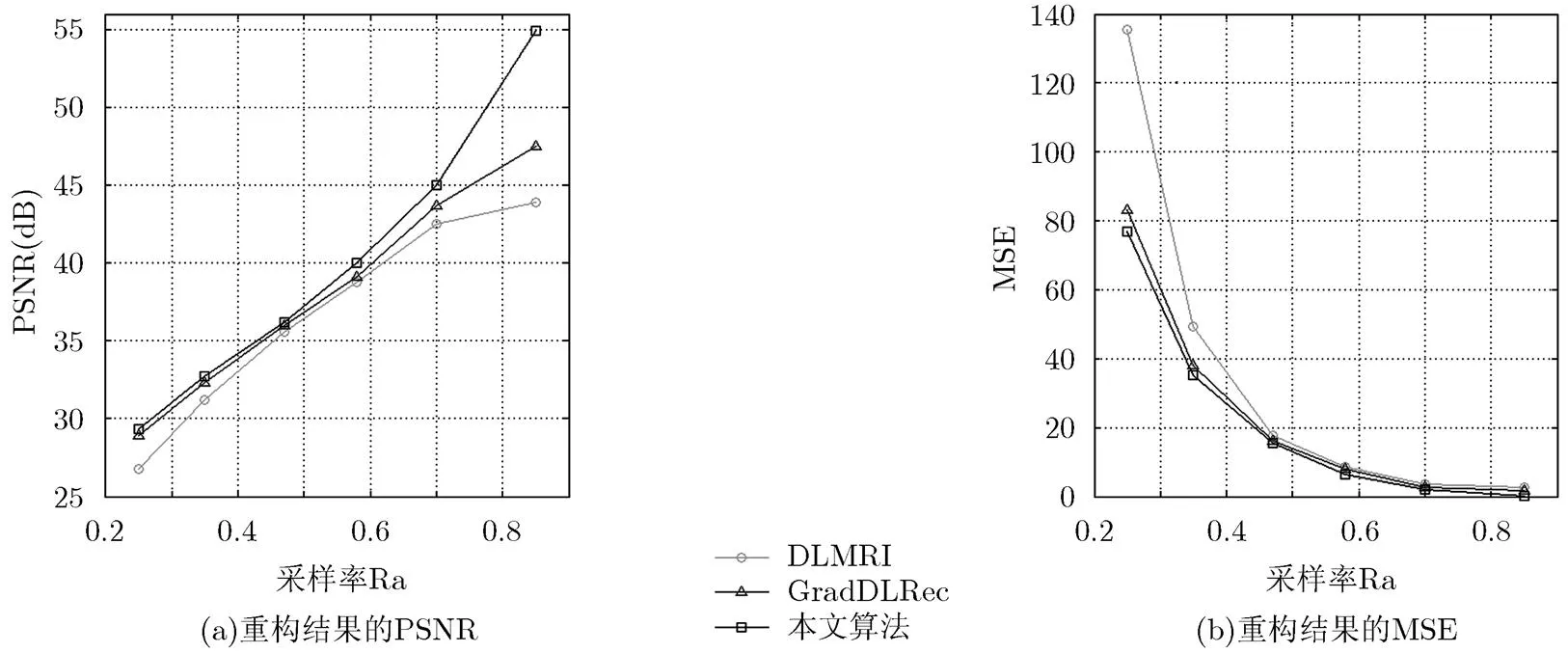
图3 3种算法重构月球微波辐射图像的PSNR和MSE结果
通过分析表4,表5,图5(a)和图5(b)的实验结果可知,对于重构的地球微波辐射图像,无论从主观视觉和客观PSNR值以及MSE值来看,本文算法比DLMRI算法和GradDLRec算法在重构图像效果上都有显著提高,而且本文算法保留了图像的大部分细节信息,获得了更加清晰的微波辐射图像。由图5(b)可知:相对应的MSE变化曲线趋势和PSNR变化曲线趋势恰恰相反。因此,由上述结论可知:本文算法在重构图像质量上优于DLMRI算法和GradDLRec算法,能够得到更高分辨率的微波辐射图像。

图4 地球微波辐射重构图像
表2重构月球图像中,3种算法在6个采样率下的PSNR值(dB)
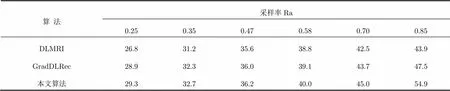
算法采样率Ra 0.250.350.470.580.700.85 DLMRI26.831.235.638.842.543.9 GradDLRec28.932.336.039.143.747.5 本文算法29.332.736.240.045.054.9
表3重构月球图像中,3种算法在6个采样率下的MSE值
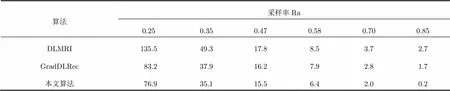
算法采样率Ra 0.250.350.470.580.700.85 DLMRI135.549.317.88.53.72.7 GradDLRec 83.237.916.27.92.81.7 本文算法 76.935.115.56.42.00.2
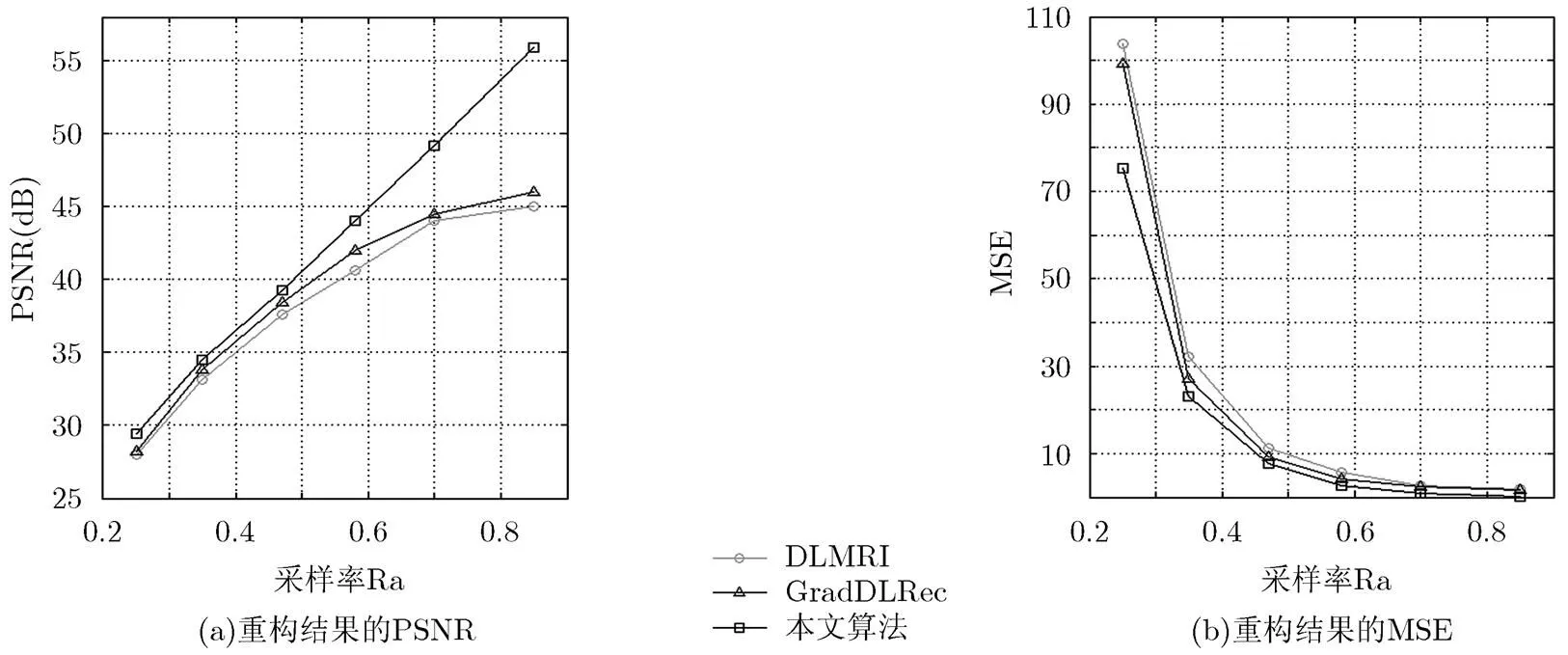
图5 3种算法重构地球微波辐射图像的PSNR和MSE结果

表4 重构地球图像中,3种算法在6个采样率下的PSNR值(dB)
表5重构地球图像中,3种算法在6个采样率下的MSE值

算法采样率Ra 0.250.350.470.580.700.90 DLMRI103.832.111.35.72.62.0 GradDLRec 99.427.0 9.34.12.31.6 本文算法 75.323.2 7.72.70.80.2
在采样率为0.58时,本文算法重构月球和地球微波辐射图像的PSNR分别为:40.0 dB, 44.0 dB,与文献[5](高斯随机观测)采用级联字典与OMP重构月球和地球微波辐射图像的结果:35.72 dB, 44.53 dB接近。压缩感知理论指出,在相同条件下,傅里叶随机抽取比高斯随机观测需要更高的采样率,因此本文提出的多稀疏基字典学习方法优于文献[5]的方法。
4.2噪声灵敏度仿真分析
为了测试噪声灵敏度,在稀疏采样中增加零均值的高斯噪声。通过控制高斯随机噪声的方差值,仿真3种算法(DLMRI算法、GradDLRec算法和本文算法)的PSNR与噪声方差值的关系,从而分析不同方法的噪声灵敏度。本文实验方差值分别设置为:0.1, 1.0, 2.0, 5.0, 8.0, 10.0。
图6(a)和图6(b)分别表示采样率为0.25和0.58时,DLMRI, GradDLRec和本文算法的PSNR随噪声方差值变化的趋势图。从仿真结果中,我们可以看出本文算法的PSNR随噪声变化的幅度最小,且在相同采样率和相同噪声方差下PSNR的值最大,因此,本文算法的噪声稳定性好,受噪声干扰小。
4.3 计算复杂度分析
DLMRI算法包括稀疏表示和图像重构两个阶段,其计算复杂度为O(0); GradDLRec算法主要包括稀疏表示、图像重构,计算复杂度分别为O(0), O(g()),其中,算法总体的计算复杂度取决于稀疏表示复杂度O(0)。本文算法是在GradDLRec算法的稀疏基字典上增加了小波基,构成差分与小波基的级联字典,仅对GradDLRec算法的稀疏基字典长度做了线性扩展,因此,本文算法的计算复杂度近似为O(0)。为验证本文算法的计算复杂度,对GradDLRec算法和本文算法的运行时间进行了仿真。仿真实验是在Matlab 8.0版本(R2012b)中运行,计算机配置为Intel Core i7 CPU, 2.70 GHz主频,8 G内存,64位Windows 7操作系统。为了消除随机的影响,仿真实验对两种算法的运行时间进行10次统计平均,GradDLRec算法与本文算法平均运算时间分别为151 s和167 s,从而验证了本文算法的计算复杂度近似为O(0)。
5 结束语
考虑微波辐射图像在总体差分域和小波中都具有可压缩特性,本文提出混合正交基的字典学习微波辐射图像重构方法。通过级联总体差分和小波稀疏表示微波辐射图像,建立混合稀疏基的字典学习微波辐射图像模型,利用Bregman和交替迭代算法分解为3个子问题,通过分别求解3个子问题有效重构微波辐射图像。仿真实验结果表明,本文提出的算法相比DLMRI和GradDLRec算法具有更好的重构图像效果,获得了更加清晰、分辨率更高的微波辐射图像;同时在噪声稳定性上也要优于DLMRI和GradDLRec两种算法,具有很好的抗噪声干扰性。同时,在重构性能方面,本文算法优于级联字典与OMP重构方法。由于采用了多稀疏基的K-SVD算法训练字典,本文算法运行时间较长。后续工作将优化本文算法的重构时间和参数设置,进一步推向实际工程应用。
[1] SWIFT C T, LEVINE D M, and RUF C S. Aperture synthesis concepts in microwave remote sensing of the Earth[J]., 1991, 39(12): 1931-1935. doi: 10.1109/22.106530.
[2] KERR Y H, WALDTEUFEL P, WIGNERON J,The SMOS mission: New tool for monitoring key elements of the global water cycle[J]., 2010, 98(5): 666-687. doi: 10.1109/JPROC.2010.2043032.
[3] DONOHO D L. Compressed sensing[J]., 2006, 52(4): 1289-1306. doi: 10.1109/TIT.2006.871582.
[4] LIU Y DE, DE VOS M, GLIGORIJEVIC I,Multi-structural signal recovery for biomedical compressive sensing[J]., 2013, 60(10): 2794-2805. doi: 10.1109/TBME.2013.2264772.
[5] 朱路, 刘江锋, 刘媛媛, 等. 基于稀疏采样与级联字典的微波辐射图像重构方法[J]. 微波学报, 2014, 30(6): 41-45.
ZHU Lu, LIU Jiangfeng, LIU Yuanyuan,. Microwave radiation image reconstruction method based on the sparse sampling and combined dictionary[J]., 2014, 30(6): 41-45.
[6] AHARON M, ELAD M, and BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]., 2006, 54(11): 4311-4322. doi: 10.1109/TSP.2006.881199.
[7] 练秋生, 石保顺, 陈书贞. 字典学习模型、算法及其应用研究进展[J]. 自动化学报, 2015, 41(2): 240-260. doi: 10.16383/ j.aas.2015.c140252.
LIAN Qiusheng, SHI Baoshun, and CHEN Shuzhen. Research advances on dictionary learning models, algorithms and applications[J]., 2015, 41(2): 240-260. doi: 10.16383/j.aas.2015.c140252.
[8] RAVISHANKAR S and BRESLER Y. MR image reconstruction from highly undersampled k-space data by dictionary learning[J]., 2011, 30(5): 1028-1041. doi: 10.1109/TMI.2010.2090538.
[9] LIU Q, WANG S, YING L,. Adaptive dictionary learning in sparse gradient domain for image recovery[J]., 2013, 22(12): 4652-4663. doi: 10.1109/TIP.2013.2277798.
[10] HUANG Y, PAISLEY J, LIN Q,. Bayesian nonparametric dictionary learning for compressed sensing MRI[J]., 2014, 23(12): 5007-5019. doi: 10.1109/TIP.2014.2360122.
[11] THIAGARAJAN J J, RAMAMURTHY K N, and SPANIAS A. Learning stable multilevel dictionaries for space representations[J].&, 2015, 26(9): 1913-1926.doi: 10.1109/ TNNLS.2014.2361052.
[12] SHEN L, SUN G, HUANG Q,. Multi-level discriminative dictionary learning with application to large scale image classification[J]., 2015, 24(10): 3109-3123. doi:10.1109/TIP.2015.2438548.
[13] LU C, SHI J, and JIA J. Scale adaptive dictionary learning[J]., 2014, 23(2): 837-847. doi: 10.1109/TIP.2013.2287602.
[14] MAHMOUD N, FAEZEH Y, and HUSEYIN O. A strategy for residual component-based multiple structured dictionary learning[J].2015, 22(11): 2059-2063. doi: 10.1109/LSP.2015.2456071.
[15] 朱路, 陈素华, 刘江锋, 等. 基于变密度稀疏采样的微波辐射干涉测量反演成像方法[J]. 计算机应用研究, 2015, 32(4): 1236-1239. doi: 10.3969/j.issn.1001-3695.2015.04.066.
ZHU Lu, CHEN Suhua, LIU Jiangfeng,Microwave radiation interferometry inversion imaging method based on variable density sparse sampling[J]., 2015, 32(4): 1236-1239. doi: 10.3969/j.issn. 1001-3695.2015.04.066.
[16] YIN W, OSHER S, GOLDFARB D,Bregman iterative algorithms for1-minimization with applications to compressed sensing[J]., 2008, 1(1): 143-168. doi: 10.1137/070703983.
Microwave Radiation Image Reconstruction Method Based on the Mixed Sparse Basis Dictionary Learning
ZHU Lu SONG Chao LIU Yuanyuan HUANG Zhiqun WANG Yang
(,,330013,)
At present, the amount of data collection of microwave radiometric imaging system in one snapshot is massive, so it is difficult to achieve the high spatial resolution by conventional microwave radiation imaging method based on the Nyquist sampling. According to the situations of microwave radiation interferometry conducted in the frequency domain, super sparse interferometry is adopted based on the optimal random Fourier sampling to sparsely project microwave radiation image, reducing the amount of data collection. Considering that the microwave radiation image has the character of compressibility in the total variation and microwave domain, the model of microwave radiation image reconstruction method is proposed based on the learning dictionary of mixed sparse basis of total variation and the wavelet, and the microwave radiation image is reconstructed by the Bregman and alternate direction method. The simulation results show that the proposed algorithm is better than the DLMRI algorithm and GradDLRec algorithm from two aspects of image reconstruction and noise sensitivity.
Microwave Radiation Image (MRI); Super sparse interferometry; Mixed orthogonal basis learning dictionary; Alternate direction method
TP751
A
1009-5896(2016)11-2724-07
10.11999/JEIT160104
2016-01-21;改回日期:2016-08-03;
2016-10-09
朱路 luyuanwanwan@163.com
国家自然科学基金(31101081, 61162015),江西省自然科学基金(20161BAB202061)
The National Natural Science Foundation of China (31101081, 61162015), The Natural Science Foundation of Jiangxi Province (20161BAB202061)
朱 路: 男,1976年生,副教授,博士,硕士生导师,研究方向为无线传感器网络、压缩感知、图像处理.
宋 超: 男,1988年生,硕士生,研究方向为压缩感知、图像处理.
刘媛媛: 女,1978年生,副教授,硕士,硕士生导师,研究方向为无线传感器网络、压缩感知.

