基于供应商联盟的混合补货方式下ATO供应链补货策略
李宇雨,黄 波
基于供应商联盟的混合补货方式下ATO供应链补货策略
李宇雨1,黄 波2
(1.重庆师范大学计算机与信息科学学院,重庆400047;2.重庆大学经济与工商管理学院,重庆400044)
考虑ATO供应链中组装商通过拉动式和推动式两种补货方式分别从两个供应商处采购零部件,供应商可以结成联盟与其进行谈判,构建了相应的ATO供应链Stackberg非合作博弈和讨价还价合作博弈模型,研究了ATO供应链零部件生产及补货策略,收益分配策略和供应商结盟策略,并比较了两种决策模式下的供应链最优策略,分析了各方议价能力等对最优策略的影响。研究发现,ATO供应链通过合作博弈制定的策略实现了非合作博弈的Pareto改进;组装商的谈判顺序决策权能为其在谈判中带来额外收益,供应商通过结盟参与谈判则可对此有效化解,并在供应商议价能力均较强的情况下,提高所有供应商的利润。
ATO供应链;供应商联盟;Stackberg博弈;讨价还价博弈;补货策略
0 引言
随着企业间竞争转变为基于时间和客户需求的竞争,在为顾客提供定制化产品的同时,提高产成品响应速度,成为企业增强竞争力的重要手段。按订单装配(Assemble - to - Order,ATO)因其能以较低的成本快速响应市场变化成为许多企业优先考虑的生产方式之一(如电脑、汽车、摩托车等)[1,2]。在ATO模式下,由于企业是接到客户订单后才开始组装最终产品,因此原材料或零部件的及时供应是系统顺利运行的关键[3]。
ATO供应链主要采用两种补货方式:推动式补货方式和拉动式补货方式。在推动式补货方式下,供应商因拥有某些核心技术,在与制造商的合作中具有一定优势,议价能力较强,会由组装商保有零部件库存并承担相应库存风险[4];在拉动式补货方式下,供应商在合作中处于弱势,议价能力较弱,会由其保有零部件库存并承担相应库存风险[5]。现实ATO供应链中,制造商通常会同时采用拉动式和推动式补货方式,如国内的一些电脑生产商从多家供应商处购买零部件进行组装生产,在与处理器供应商Intel、AMD等芯片供应商的合作中处于弱势,采用推动式补货方式,由组装商承担库存风险;而在与光驱、机箱、电源等供应商的合作中处于强势,则与供应商签订拉动式补货协议,由供应商保有库存并承担库存风险。因此,有必要对混合补货方式下的供应链补货策略进行研究。
国内外现有相关研究主要集中于单一补货方式(推动式或拉动式)下的ATO供应链零部件补货及分配策略。如Zhao[6]考虑多产品多零部件ATO系统中,组装商采用推动式补货和连续性检查库存管理策略,研究了产品需求服从复合泊松过程,零部件补货提前期随机情况下的补货策略;ElHafsi[7]则研究了单产品多零部件ATO组装商,在产品需求服从复合泊松过程情况下的推动式补货策略以及供应商零部件生产策略;Karaarslan[8]考虑ATO组装商用两个零部件组装生产1个产成品,且采用周期性检查库存管理策略和推动式补货策略,其中1种零部件补货提前期长、保管费高且检查周期短,研究了组装商在产品需求随机且允许缺货滞后供给情况下的补货策略;Doğru[9]考虑ATO组装商用2种专用零部件和1种通用零部件组装2种产成品,零部件补货提前期相同,运用随机规划研究了组装商零部件推动式补货策略;Bernstein[10]研究了推动式补货方式下,多种产成品共享一种通用零部件的ATO组装商,如何基于产品需求预测制定通用零部件的补货及分配策略;Bernstein和Decroix[11]则研究了拉动式补货方式下多层次ATO系统中,供应商零部件产量和价格决策;Wang和Gerchak[12]分析了拉动式补货方式下,面临随机性需求的ATO系统组装商和供应商零部件补货及定价策略。
近年来,学者们逐渐开始对拉动与推动混合补货方式下ATO系统零部件生产及补货策略进行研究,如李宇雨等[13]考虑由一个最终产品制造商与两个零部件供应商组成的ATO系统,制造商分别采用拉动式和推动式补货方式向不同的供应商采购零部件,运用Stacklberg等非合作博弈研究了ATO供应链零部件生产、补货策略,但该文考虑组装商和供应商是一种完全竞争的关系;但斌等[14]则研究了由一个组装商和多个供应商组成的ATO供应链,如何以供应链总利润最大化为目标,选择拉动式和推动式补货方式,以及相应的生产及补货批量,但该文考虑组装商与供应商之间是一种完全的合作关系,且没有研究供应链合作能否实现,以及如何通过合理的零部件价格和利润分配促进供应链合作的实现。事实上现代市场竞争是整个供应链之间的竞争,供应链上下游企业非常注重加强合作,以增强供应链竞争力,在最大化供应链利润的同时最大化自身利润,实现供应链各方的共赢。因此,供应链企业间的关系应该是一种竞争与合作并存的竞合关系。
此外,ATO供应链中,组装商是从多个供应商处采购零部件进行组装,供应商为了增加与组装商的议价能力会结成联盟,共同与组装商进行讨价还价,如电子元件[15],汽车配件供应商联盟[16]。Nagarajan和Sošić[17]考虑产品需求确定的ATO供应链由一个组装商和多个供应商组成,供应商结成动态联盟与组装商展开竞争,研究了以供应商联盟为领导者的Stacklberg博弈,以组装商为领导者的Stacklberg博弈,以及双方同时展开行动的纵向纳什博弈等3种模式下的供应链联盟稳定性;Sošić[18]则在文献[17]的基础上,进一步考虑ATO供应链产成品需求不确定,研究了同样3种模式下的供应链联盟稳定性。
基于此,本文考虑ATO供应链中组装商同时采用拉动式和推动式补货方式从供应商处采购零部件,供应商可以结成联盟,共同与组装商进行谈判,针对ATO供应链企业间竞合关系的特征,通过构建基于供应商联盟的混合补货方式下ATO供应链Stackberg非合作博弈和讨价还价合作博弈模型,研究ATO供应链零部件生产及补货策略,收益分配策略和供应商结盟策略,并通过理论和数值仿真算例分析,找出ATO供应链最优策略以及供应商的结盟条件,比较两种决策模式下的供应链最优策略,分析主要参数对最优解的影响,为ATO供应链组装商和零部件供应商制定相关策略提供理论依据。
1 问题描述及模型建立
1.1 问题描述
ATO供应链中,一些零部件供应商在行业中处于垄断地位,议价能力强(如电脑的芯片供应商),组装商一般采取推动式补货方式向其补货,即,双方谈判确定出零部件的补货价格和补货批量,并且由组装商保有零部件库存,承担库存风险和零部件积压损失;而一些零部件供应商所处行业竞争激励,缺乏垄断力和议价能力(如电脑的机箱供应商),组装商一般采取拉动式补货方式向其补货即,双方谈判确定出零部件的补货价格,零部件产量则由供应商决定,并由其保有零部件库存,承担承担库存风险和零部件积压损失。
ATO供应链可以采用两种模式进行合作,一种是组装商及供应商各以自身利润最大化为目标,通过Stackelberg博弈,决定零部件补货批量和价格;另一种是以供应链整体利润最大化为目标,决定零部件补货批量,再通过讨价还价博弈,决定零部件价格。
在组装商及供应商各以自身利润最大化为目标,通过Stackelberg博弈,决定零部件补货批量和价格的情况下,ATO供应链合作的决策分为三个阶段:第一阶段,由供应商1制定零部件1价格;第二阶段,由组装商根据零部件1价格、产品单位组装成本和市场需求等确定零部件1补货量及零部件2价格;第三阶段,由供应商2根据组装商给出的零部件2价格制定其零部件2批量。
ATO供应链以整体利润最大化为目标进行合作过程如下:首先,零部件供应商确定是否结盟参与供应链合作。接着,组装商与零部件供应商为了实现供应链及其自身利润的最大化,以ATO供应链总利润最大化为目标一同制定市场策略,包括:零部件产量,以及供应商不结盟情况下,组装商与供应商的谈判顺序,由于组装商是ATO供应链的核心企业,因此,拥有谈判顺序的决策权。接下来,若供应商不结盟,则组装商按谈判顺序与供应商分别进行谈判,通过讨价还价,确定出供应商的零部件价格及ATO供应链各方所分得利润,并签订契约;若供应商结盟参与供应链合作,则组装商与供应商联盟进行谈判,通过讨价还价,确定组装商与供应商联盟的利润分配,再由供应商联盟内部通过讨价还价确定各供应商的零部件价格及其分得利润,并分别与组装商签订契约;最后,供应商按契约规定生产出零部件,组装商则分别以推动式和拉动式补货方式进行零部件补货,并根据产品订单进行组装和销售,并实现各自的利润。
显然,组装商和零部件供应商的议价能力,供应商是否结盟,供应商不结盟情况下的谈判顺序都将对ATO供应链各方利润造成很大影响。本文将通过建立基于供应商联盟的拉动与推动混合补货模式下ATO供应链讨价还价合作博弈模型,研究ATO供应链最优零部件生产和补货策略,利益分配策略,以及供应商的结盟策略,分析供应链各方议价能力和谈判顺序等对以上策略的影响。
1.2 模型建立
供应商为了增强对组装商的议价能力,首先需要决定是否以结盟方式参与ATO供应链合作。接着,为了实现ATO供应链合作的最优,组装商和供应商(或供应商联盟)以供应链期望利润最大化为目标,确定零部件1和零部件2的生产及补货批量和,以及供应商不结盟情况下的谈判顺序。接下来,若供应商不结盟则组装商分别与供应商1和2进行谈判,通过讨价还价确定零部件价格及各自利润;若供应商结盟则先由联盟与组装商通过讨价还价确定利润分配,再由供应商之间通过讨价还价确定零部件价格及相应利润。谈判完成后,供应商1和2分别以和的单位生产成本按各自的补货批量制造零部件,零部件生产完成后,供应商1将整批零部件以的价格交付给组装商,并由其保管零部件库存;供应商2则需保管零部件库存,只在组装商时以价格向其交付零部件。组装商在接到产品订单后,以单位组装成本组装产成品,组装完成即以销售价格交付给最终用户。季末没有组装的零部件残值为0,组装商将为此承担零部件1的积压成本,供应商2则承担零部件2的积压成本。
产成品的销售价格和市场需求,组装商单位组装成本和议价能力,供应商单位生产成本和议价能力,供应商是否结盟,以及ATO供应链谈判顺序等均是所有企业共同知识。
由以上可知,ATO供应链期望总利润为:
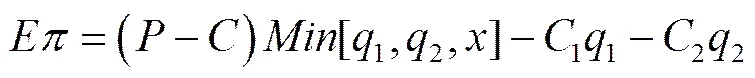
由于组装商需在销售季节之初就向供应商1订货,且拥有并负责保管零部件1的库存,承担相应库存风险,因此供应商1的利润在销售季节之初即可确定,为:
(2)
由于供应商2拥有并负责保管零部件2的库存,承担相应库存风险,因此供应商2的利润不确定,其期望利润为:
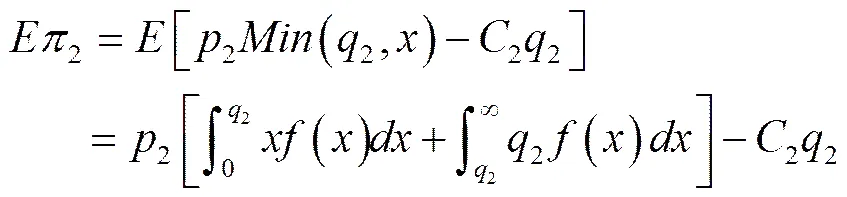
组装商拥有并负责保管零部件1的库存,承担相应库存风险,因此组装商的利润不确定,其期望利润为:
(4)
本文接下来将分别讨论两种决策模式下的最优解。
2 组装商利润最大化下的最优解
在组装商及供应商各以自身利润最大化为目标,通过Stackelberg博弈,决定零部件补货批量和补货价格的情况下,ATO供应链合作的决策分为三个阶段:第一阶段,由供应商1制定零部件1价格;第二阶段,由组装商根据零部件1价格、产品单位组装成本和市场需求等确定零部件1补货量及零部件2价格;第三阶段,由供应商2根据组装商给出的零部件2价格制定其零部件2的生产批量。本部分则将采用逆向归纳法分析ATO供应链最优解。
首先,供应商2以自身利润最大化为目标,制定零部件2最优批量,求解,可以得到为满足下式的解。
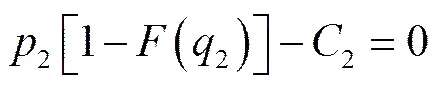
(6)
(6)式为供应商2的反应函数,即,当组装商给定一个零部件2的价格,供应商2就有一个对应的零部件2批量使其利润最大。
由于产品市场需求以及供应商2的成本为共同知识,组装商就知道供应商2的反应函数,就会据此以自身利润最大化为目标,确定零部件2价格以及零部件1批量。求解可得:

求解(7)式可得组装商的零部件2最优价格为
(8)
(8)式表明组装商制定的零部件2最优价格与零部件1价格为一一对应关系,即,当供应商1给定一个零部件1价格,组装商就能找到一个零部件2最优价格使其自身利润最大。
由于1个产品是由1个零部件1和1个零部件2组装而成,且组装商承担着零部件1的库存风险,因此,必然向供应商1采购不超过的零部件1,即;同样,供应商2承担着零部件2的库存风险,且知道组装商的零部件1补货批量,因此,必然生产不超过的零部件2,即,博弈的最后结果就是,即:
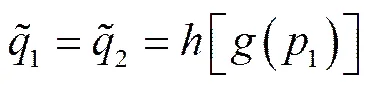
同样,供应商1也知道组装商的反应函数,即(9)式,就会据此以自身利润最大化为目标制定零部件1价格,将(9)式代入(2)式,求解可得:
(10)
结论1 零部件2最优生产批量随零部件2价格提高而增加。
结论1表明,在混合补货方式的ATO系统中,与组装商签订拉动式补货协议的供应商,应随其零部件价格的提高而增加生产批量。
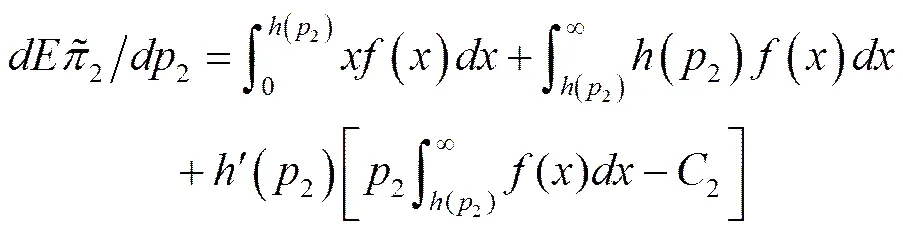
结论2表明,与组装商签订拉动式供货协议的供应商,其利润在产品缺货概率较大时,会随着其零部件价格的提高而增加,换言之,签订拉动式协议下供货商应在此情况下,提高零部件价格,以获取更高利润。
3 供应链利润最大化下的最优解
在ATO供应链以整体利润最大化为目标进行决策的情况下,ATO供应链合作顺序为,首先由组装商和供应商1和2以供应链期望总利润最大化为目标,确定零部件1和2的产量,由于产成品是由1个零部件1和1个零部件2组成,若两种零部件的产量不相等,则必然有1种零部件会因没有配套零部件而被浪费,造成不必要的损失和成本,因此,ATO供应链必然生产相同数量的零部件1和2,即。求ATO供应链期望总利润关于零部件1和2产量的一阶偏导数等于0的解,即,可得:
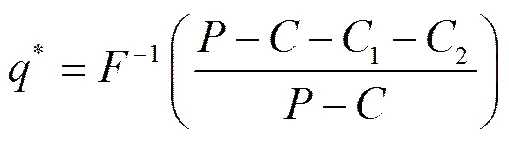
(12)
由(11)式可得结论3如下。
结论3 ATO供应链中供应商最优零部件产量随产成品销售价格的提高而增加,随组装商制造成本和供应商生产成本的提高而减少。
结论3表明,随着产成品销售价格的提高,ATO供应链因零部件供给不足而导致的利润损失和缺货成本上升,所以就应该提高零部件产量以降低缺货概率和成本;而随着组装商组装成本提高,ATO供应链利因零部件供给不足而导致的利润损失和缺货成本下降,随着供应商生产成本提高,ATO供应链积压成本上升,所以就应该减少零部件产量以降低积压概率和成本。
3.1 供应商不结盟情况下的最优解分析
ATO供应链在确定了最优零部件产量及相应的期望总利润后,由组装商分别与供应商1和2进行序贯谈判,以讨价还价方式确定各自的(期望)利润、和,显然,。因为组装商是与供应商1和2进行序贯谈判,所以ATO供应链合作是由两次双人讨价还价博弈组成,每次讨价还价博弈均为:

s.t.,
组装商以及供应商1和2为了能从供应链合作中获得更高的利润,往往会在谈判前向其他企业发出通牒(commitment),宣告其参与供应链合作的利润不能低于一个最低值,,否则,将退出合作。当然,这种通牒并非绝对可置信,参与者完全有可能在谈判中做出让步和妥协,接受低于该最低值的分配方案,这种妥协行为就会导致其声誉等方面的损失,从而承担一定的“妥协成本”。显然,当参与者通过讨价还价获得的利润不低于其最低值时就不存在让步和妥协行为,也就没有妥协成本产生,即时,;当参与者在谈判中做出让步和妥协,接受了低于其最低要求值时,就会承受一定妥协成本,即时,,其中,,为单位妥协成本。该式表明,参与者因妥协所付出成本与其妥协程度正相关(即其要求的最低值与实际分得的期望利润之间差距)。由此可得:


(15)

,(17)
供应链合作过程中,参与各方确定了供应链零部件产量及相应最优期望总利润后,由组装商决定谈判顺序,并按照谈判顺序分别与两个供应商进行两轮谈判,通过讨价还价确定零部件采购价格及相应的利润分配。在第1轮谈判中,双方就供应链合作期望总利润进行讨价还价,确定出供应商1或2的零部件采购价格及其相应所分得的利润,;以及第2轮谈判中所需进行分配的利润;在第2轮谈判中,双方就利润进行讨价还价,确定出该供应商的零部件采购价格及相应的各自利润和。
本文进一步考虑第1轮谈判双方约定,该轮谈判的协议只有在组装商的第2轮谈判也达成协议才正式生效,以避免第2轮中“敲竹杠”行为的产生。如组装商在第1轮谈判达成协议后就向该供应商下了零部件订单,并需承担违约赔偿责任,另一个供应商就可能在第2轮谈判中进行“敲竹杠”,获得额外收益。
由此可得引理1如下。
由引理1可以看出,无论组装商按照什么样的顺序进行谈判,其所获利润相同,因此,其对谈判顺序没有偏好。但对供应商()而言,若能在第1轮与组装商谈判,将获得更多的利润,因此,供应商都更愿意在第1轮与组装商谈判,也就愿意在确定谈判顺序时向组装商许诺,以向其转让部分利润为代价,换取在第1轮进行谈判的权利。
由此可得引理2如下。
引理2表明,供应商1和供应商2在与组装商谈判中,会因谈判顺序的提前而额外获利(即,谈判顺序后移而受损),而谈判顺序由组装商来决定,所以,供应商1和2就会为了获得(或保住)其在第1轮谈判的位置,而向组装商让利。组装商也会对此加以充分利用,要求供应商1和供应商2让利,以最终获得更多利润。
由此可得结论4如下。
结论4表明,由于供应商无权决定谈判顺序,因此,无论参与第几轮谈判,均只能获得在第2轮参与谈判的利润,而组装商则因供应商的让利,而获得额外的利润,提高其期望利润。

(19)
由(18)式和(19)式可得结论5如下。
结论5表明,组装商对某供应商的议价能力越强(即该供应商对组装商的议价能力越弱),组装商在于求该供应商谈判中越能要求其降低零部件价格以获得更多利润;而另一个供应商自然就会要求从组装商处分得一部分增加的利润,因此,就会提高其零部件转移价格。
证明:求组装商和供应商1和2的期望利润关于组装商议价能力()的一阶偏导数可得
3.2 供应商结盟情况下的最优解分析
在ATO供应链合作中,供应商有时会与其它供应商结成供应商联盟,去和组装商进行谈判,以提升对组装商的议价能力,提高自身利润。

供应商之间的利润分配仍采用讨价还价的谈判方式,且供应商之间的议价能力为:
(21)

由(17)、(21)和(22)式可知,供应商之间的议价能力与供应商对组装商议价能力之间的关系为:
(23)
证明:当供应商将结成联盟参与ATO供应链合作时,首先是供应商联盟与组装商通过讨价还价分配利润,组装商分得利润,供应商联盟则分得利润,接着,供应商之间再通过讨价还价进行利润分配,则供应商()的期望利润为。由结论2可知,供应商独立参与ATO供应链合作时的期望利润为。
结论8 供应商结盟参与ATO供应链合作情况下,组装商和供应商()的收益分别为和。
证明:结论8的证明过程由结论7证明过程可得。结论8证毕。
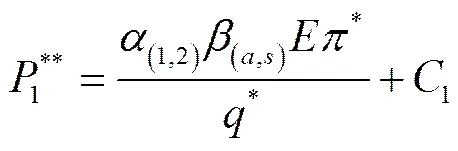
(25)
由(18)式和(19)式可得结论9如下。
结论9表明,供应商对另一个供应商议价能力越强,另一个供应商对该供应商议价能力就越弱,该供应商就能在供应商联盟内部谈判中分得更多的利润,即可以向组装商索取更高的零部件价格,由于供应商联盟与组装商之间的议价能力不变,供应商联盟从ATO总利润中分得的利润不变,因此,另一个供应商的零部件价格和利润就会降低,组装商的利润则保持不变。组装商对供应商联盟的议价能力越强(即,供应商联盟对组装商的议价能力越弱),组装商在谈判中分得利润越多,供应商联盟分得利润越少,而供应商之间议价能力和利润分配比例未变,因此,供应商所的零部件价格和利润均会降低。
4 仿真分析
求解可得,当组装商及供应商以各自利润最大化为目标,采用Stackberg非合作博弈进行决策时,ATO供应链最优解分别为:零部件1价格,零部件2价格;零部件批量,供应商1利润,供应商2利润,组装商利润。
当ATO供应链以供应链整体利润最大化为目标,采用讨价还价博弈进行决策时,组装商和供应商()的妥协成本系数分别为:,和,由(16)、(17)、(20)、(21)和(22)式可得,组装商对供应商及供应商联盟的议价能力,供应商和供应商联盟对组装商的议价能力,以及供应商之间的议价能力分别为:
若供应商独立参与ATO供应链合作,则由结论4和(18),(19)式可得供应商()的最优零部件价格分别为和,组装商期望利润和供应商的利润分别为,和。
对比两种博弈结果可以发现,ATO供应链采用Stackberg非合作博弈进行决策时,最终的零部件产量仅为仅为ATO供应链最优零部件产量的约40%,ATO供应链的总利润仅为ATO供应链最大期望利润的63%,组装商和供应商的利润也分别小于以ATO整体利润最大化进行决策时的各自利润,因此,供应商结盟参与ATO供应链合作,并通过讨价还价合作博弈制定ATO供应链零部件生产及补货策略,提高了ATO供应链所有参与主体的期望利润,实现了ATO供应链的Pareto改进。
由表1可以发现,正如结论4指出,组装商对供应商1议价能力越强,零部件1的价格越低,供应商1利润越少;零部件2的价格则越高,供应商2的利润越多;当组装商议价能力比供应商2强时,组装商期望利润越多,反之,组装商议价能力比供应商2弱时,组装商的期望利润越少。由于一直得到满足,因此,供应商均会结盟参与ATO供应链合作。
此外,由(14)式可知,组装商对供应商1议价能力越强,其对供应商联盟的议价能力也越强,因此,由表1还可以发现,正如结论7指出,随着组装商对供应商联盟的议价能力的增强,其期望利润变得越来越多。
表1 对零部件价格及相应利润的影响
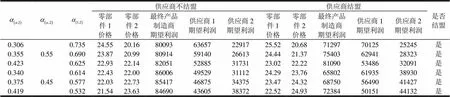
表1 对零部件价格及相应利润的影响
供应商不结盟供应商结盟是否结盟 零部件1价格零部件2价格最终产品制造商期望利润供应商1期望利润供应商2期望利润零部件1价格零部件2价格最终产品制造商期望利润供应商1期望利润供应商2期望利润 0.3060.550.73524.5520.1680093636572291725.5220.68712977012525245是 0.3550.69023.8720.9980914591402661324.4421.37754036294128323是 0.4230.62522.9322.1482051528853173123.0222.22810905348632091是 0.3400.450.61422.4322.0086006495293111224.2923.76658026193538930是 0.3750.57722.0322.7385417468753437523.4724.32687505649041427是 0.4190.53221.5423.6384690436053837222.5224.93723845015144132是
5 结论
本文考虑ATO供应链中组装商分别通过拉动式补货和推动式补货方式从两个供应商处采购零部件,供应商可以通过结盟与其进行谈判,分别构建了ATO供应链Stackberg非合作博弈和讨价还价合作博弈模型,研究了ATO供应链零部件生产及补货策略,以及相应的收益分配策略和供应商结盟策略,得出了ATO供应链的最优零部件生产和补货策略,收益分配方案,以及供应商是否结盟的条件,并比较了两种决策模式下的供应链最优策略,分析了组装商,供应商和供应商联盟议价能力对ATO供应链最优策略的影响。
研究发现,ATO供应链通过合作博弈制定的相关策略优于非合作博弈,提高了所有参与者利润,实现了Pareto改进;ATO供应链应随产成品价格上升而提高零部件产量,随零部件制造成本或产成品组装成本上升而降低零部件产量;组装商可利用其谈判顺序决策权,迫使供应商向其转让部分利润,而供应商结盟与其谈判则可有效化解组装商的这一优势,并在供应商议价能力均较强的情况下,提高所有供应商的利润;在供应商不结盟情况下,组装商对某供应商议价能力越强,该供应商零部件价格及利润越低,另一供应商零部件价格及利润越高,若组装商比另一供应商议价能力强,其期望利润越高,否则越低;在供应商结盟情况下,组装商对供应商联盟议价能力越强,其期望利润越高,所有供应商的零部件价格及利润越低,供应商对另一个供应商议价能力变化会提高该供应商零部件价格及其利润,降低另一个供应商零部件价格及其利润,对组装商期望利润没有影响。
[1] 聂佳佳. 预测信息分享对制造商开通直销渠道的影响[J]. 管理工程学报, 2012, 26(2):106-112.
[2] Lu Y, Song J S, Zhao Y. No-holdback allocation rules for continuous-time assemble-to-order systems[J]. Operations Research, 2010, 58(3):691-705.
[3] 郭佳, 傅科, 陈功玉. 可变产能的按订单装配系统库存和生产决策研究[J]. 中国管理科学, 2012, 20(3):94-103.
[4] DeCroix G A, Song J S, Zipkin P H. Managing an assemble-to-order system with returns[J]. Manufacturing & service operations management, 2009, 11(1):144-159.
[5] Feng J, Liu L, Wan Y. Irreducibility of joint inventory positions in an assemble-to-order system under (r, nQ) policies[J]. Naval Research Logistics (NRL), 2012, 59(1):18-25.
[6] Zhao Y. Analysis and evaluation of an assemble-to-order system with batch ordering policy and compound Poisson demand[J]. European Journal of Operational Research, 2009, 198(3):800-809.
[7] ElHafsi M. Optimal integrated production and inventory control of an assemble-to-order system with multiple non-unitary demand classes[J]. European Journal of Operational Research, 2009, 194(1):127-142.
[8] Karaarslan A G, Kiesmüller G P, De Kok A G. Analysis of an assemble-to-order system with different review periods[J]. International Journal of Production Economics, 2013, 143(2): 335 – 341.
[9] Doğru M K, Reiman M I, Wang Q. A stochastic programming based inventory policy for assemble-to-order systems with application to the W model[J]. Operations research, 2010, 58(4-1):849-864.
[10] Bernstein F, DeCroix G A, Wang Y. The impact of demand aggregation through delayed component allocation in an assemble-to-order system[J]. Management Science, 2011, 57(6): 1154 - 1171.
[11] Bernstein F, Decroix G. Decentralized pricing and capacity decisions in a multitier system with modular assembly[J]. Management Science, 2004, 50(9):1293-1309.
[12] Gerchak Y, Wang Y. Revenue-sharing vs. wholesale-price contracts in assembly systems with random demand[J]. Production and Operations Management, 2004, 13(1):23-33.
[13] 李宇雨, 但斌, 郭钢. 拉动与推动混合供货方式下ATO系统的生产补货策略研究[J]. 管理工程学报, 2010, 24(3):144-149.
[14] 但斌, 李宇雨, 黄波. 大规模定制环境下ATO供应链的混合补货策略[J]. 计算机集成制造系统, 2011, 17(6):1271-1278.
[15] Lee P K C, Yeung A C L, Edwin Cheng T C. Supplier alliances and environmental uncertainty: an empirical study[J]. International Journal of Production Economics, 2009, 120(1):190-204.
[16] Nagarajan M, Sošić G. Game-theoretic analysis of cooperation among supply chain agents: Review and extensions[J]. European Journal of Operational Research, 2008, 187(3):719-745.
[17] Nagarajan M, Sošić G. Coalition stability in assembly models[J]. Operations Research, 2009, 57(1):131-145.
[18] Sošić G. Impact of demand uncertainty on stability of supplier alliances in assembly models[J]. Production and Operations Management, 2011, 20(6):905-920.
Replenishment Policy of ATO Supply Chain under Mixed Replenishment Mode Based on Supplier Alliance
LI Yu-yu1, HUANG Bo2
(1. College of Computer and Information Science, Chongqing Normal University, Chongqing 400047, China; 2. College of Economics and Business Administration, Chongqing University, Chongqing 400044, China)
Under the ATO (assemble-to-order) mode, a manufacturer assembles final products only after receiving orders from a customer. Therefore, it is critical for ATO supply chains to run successfully by having components supplied in time.
This paper made an assumption that an ATO supply chain consists of two component suppliers, which are Supplier 1 and Supplier 2, and one ATO manufacturer, who replenishes component 1 from Supplier 1 by using push replenishment mode, and component 2 from Supplier 2 by pull replenishment mode. Suppliers can form an alliance to negotiate with an ATO manufacturer. We propose a Stackelberg game model and a replenishment bargaining model of ATO supply chains under the mixed replenishment mode. Supplier alliance is proposed to study component production and replenishment policy, profit-sharing policy and suppliers’ alliance policy.
In the Stackelberg game, ATO manufacturers and component suppliers decide no replenishment quantities and prices of Component 1 and Component 2 in order to maximize their own profit. There are three stages of decision-making in the Stackelberg game. In the first stage, Supplier 1 decides the price of Component 1. In the second stage, ATO manufacturer decides the replenishment quantity of Component 1 and the price of Component 2 according to the price of Component 1, assembly cost of unit product and market demand of products. In the third stage, Supplier 2 decides the quantity of Component 2 according to the replenishment price offered by the ATO manufacturer.
In the bargaining game, ATO manufacturer and component suppliers decide on replenishment quantity and prices of Component 1 and Component 2 in order to maximize the total profit of ATO supply chains. There are three stages of decision-making in the bargaining game for ATO supply chains. In the first stage, suppliers decide whether to form a supplier alliance. In the second stage, ATO manufacturer and component suppliers decide replenishment quantities and bargaining sequence under the condition that suppliers form no alliance. We assume that ATO manufacturer dictates the negotiation sequence as it is the core enterprise of ATO supply chain. In the third stage, under the condition that suppliers form no alliance, ATO manufacturer bargains with Suppliers 1 and 2 according to the negotiation sequence in order to decide the prices of components and their share of profits. Under the condition that suppliers form a supplier alliance, ATO manufacturer bargains with supplier alliance to decide profit shared by ATO manufacturer and supplier alliance. Suppliers decide the prices of components and their share of profits through negotiation.
Through theoretical and numerical analyses, optimal solutions of Stackelberg game model and bargaining model are obtained and compared. The impact of bargaining power of ATO manufacturer and component suppliers on optimal policy is analyzed.
It is found that optimal policy of ATO supply chains through cooperative game is Pareto improvement on those of non-cooperative game. The decision-making power on negotiation sequence owned by ATO manufacturer can bring additional profit. However, profit will be counteracted by alliance of suppliers in the negotiation process. In the case of both suppliers having stronger bargaining power, a supplier alliance will improve profit for both suppliers.
ATO (assemble-to-order) supply chain; suppler alliance; Stackberg game; bargaining game; replenishment policy
中文编辑:杜 健;英文编辑:Charlie C. Chen
F406.2
A
1004-6062(2016)02-0124-09
10.13587/j.cnki.jieem.2016.02.015
2013-05-13
2014-02-10
国家自然科学基金资助项目(71102178);中国教育部人文社科资助项目(11YJC630070)
李宇雨(1982—),女,重庆人,副教授,博士,主要研究方向为物流与供应链管理、大规模定制。

