基于-约束与区间数线性规划的钢铁供应链能源优化模型

朱小龙,丁 帅,朱卫东,彭张林,倪大伟



朱小龙1,2,丁 帅1,朱卫东1,彭张林1,倪大伟1

（1.合肥工业大学管理学院, 安徽合肥 230009; 2.安徽工商职业学院，安徽合肥231131）

由于二次能源的存在，钢铁供应链上的能源流在不同工序过程之间进行交互，存在着正向和逆向的能源流动。对钢铁供应链上能源流的优化，可以显著提高二次能源的利用效率，从而降低钢铁企业的综合能源消耗。首先，研究了钢铁供应链上的能源流情况，建立了钢铁供应链能源流模型，在此基础上考虑钢铁供应链能源优化的两重目标及相关约束因素，构建了钢铁供应链能源优化模型；其次，组合运用-约束方法和区间数线性规划方法对模型进行求解；最后，典型算例验证了该模型可以有效降低钢铁企业的能源消耗，提升能源利用效率。

钢铁供应链，能源优化，区间数线性规划，-约束方法

0引言

钢铁企业的生产系统可以抽象为物质流转变与能量流转变两个过程，这两个过程的运转将带来大量的资源消耗、能源消耗与废弃物排放。现代钢铁工业在工艺、技术与管理上均有较大地改进与提高，但日益趋增的市场需求在带动钢铁工业高速发展的同时，也对资源与能源的供应能力，以及环境的承载能力提出了严峻挑战[1]。为促进钢铁工业中资源利用率与能源利用率的提高，以及减少废弃物排放等实际问题的有效解决，很多学者从钢铁供应链优化方面展开研究，已有的工作主要集中在三个方向：物质流的研究[2-5]、能源流的研究[6-9]、物质流与能源流相互关系的研究[10-11]。这些研究主要从物质流与能源流模型、库存优化管理、钢铁工业能源利用效率等方面进行了分析，却鲜有涉及能源流上能源的优化配置问题。由于钢铁企业生产实践中，二次能源的存在，供应链上的能源流在不同工序过程之间进行交互，发生正向的和逆向的流动，对钢铁企业的能源利用产生了重要影响。因此，有必要从二次能源回收利用的视角，对钢铁供应链能源优化问题进行研究，以期通过二次能源的优化配置，降低钢铁供应链上能源消耗和能源成本，提高能源利用效率。

考虑二次能源回收利用的钢铁供应链系统中，能源优化主要有降低能耗与减少能源成本两个目标，但同时受到能源需求、能源平衡、废物排放、边界与参数等多方面因素的约束，使得钢铁供应链能源优化问题成为一个复杂的多目标优化问题。除此之外，钢铁供应链能源优化问题还受到相关政策、经济环境、市场变化等诸多不确定性因素的影响，使得钢铁供应链能源优化问题更加复杂。为厘清二次能源在钢铁供应链上的流动过程，以及二次能源的回收利用对钢铁供应链能源优化的实际效果。本文在详细分析钢铁供应链能源流的基础上，构建钢铁供应链能源流优化模型，并将-约束法与区间数线性规划方法引入到该模型的求解过程中，首先运用-约束法将钢铁供应链中的多目标优化模型转化为单目标优化模型，其次运用区间数线性规划方法求解含区间数的单目标优化模型。最后结合算例的实证研究，对模型进行进一步验证分析。

1钢铁供应链能源优化模型

1.1钢铁供应链能源流分析

在钢铁生产过程中，含碳素等能源经过投入、加工、转换等环节到能源产品的成型或排放物的释放，形成了钢铁供应链中能源的转换过程。各种能源沿着投入、转换、使用、排放的路径流动，形成了钢铁供应链上的能源流[11]。钢铁供应链上能源流推动了其物质流的流动和转变，实现了供应链上含铁等原料的物质的转换和分配，加快了供应链上资源的新陈代谢，对供应链上的能源效率提升起到决定作用。

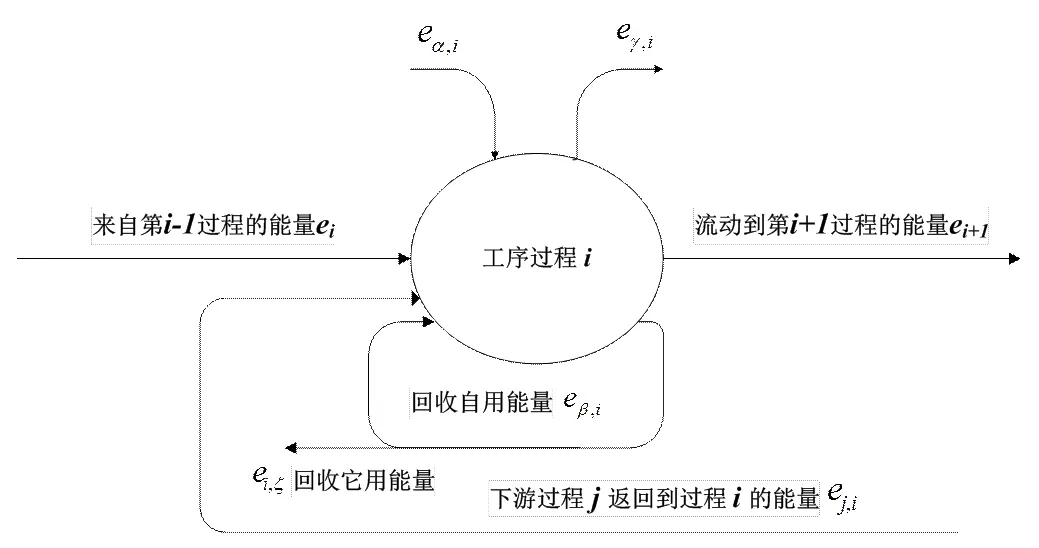
图1 单个工序过程的能源流

钢铁供应链上的能源流由正向能源流和逆向能源流组成。正向能源流是指按照供应链上各工序自上而下正向流动的能源，而逆向能源流则是指在供应链上逆向利用的二次能源，主要包括可回收的副产煤气、余热等。其中，余热是最主要的二次能源，包括烧结废气显热、焦炭显热、炼铁热风炉烟气余热、转炉煤气显热、轧钢加热炉烟气余热等[7,11]。逆向流动的二次能源与正向流动的能源一起组成了钢铁供应链上的所有能量，这些能量在不同的工序过程间进行流动。在单个工序过程上，全部能量按来源、流向和作用的不同，可以分为7股能量流，如图1所示。

单个工序过程的能量流主要包括7股能量：1）上游输入的能量，是指从第个过程带入到第过程作为原材料的能量；2）本过程输出的能量，是指产品从第过程中带走的能量；3）从外界流入的能量，是指从整个生产工序过程外部供给到第过程的燃料、电力等能量；4）损失能量，是指从第过程中排放的以及在物流输送过程中损失的能量；5）回收自用能量，是指从第过程中回收自用的二次能源；6）回收它用能量，是指从第过程中回收并用于其他过程的二次能源；7），是指由下游过程逆向返回到过程的能量。

在钢铁供应链上，存在着原材料采集、炼铁、炼钢、轧钢、产品使用等工序过程，其中，产品在原材料采集和使用两个过程中只发生了简单的物理变化，并未形成完整的能量输入与输出，因此，除了这两个过程，其他过程都蕴含着图1所示的能量流模型。考虑到不同工序过程之间的能量流转化、互动等流动过程，进一步建立完整的钢铁供应链能源流模型，该模型将所有单个工序过程的能量流进行集成，组成一个更为复杂的能源流网络体系，如图2所示。

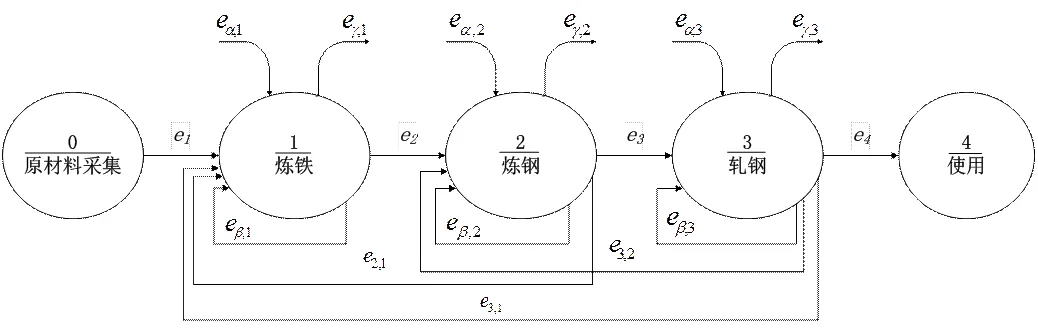
图2钢铁供应链能源流模型

钢铁供应链能源流模型展示了能源在钢铁供应链上的流动过程和流动形式。由模型可知，能源不仅在单个工序过程上进行流动，而且在上下游不同工序过程之间进行着互动与流动。因此，对钢铁供应链能源优化的研究，应立足于整个钢铁供应链能源流模型，运用优化建模理论与方法，统筹分析二次能源的回收利用对钢铁供应链能源优化的实际影响。

1.2钢铁供应链能源优化模型

图1和图2分别描绘了单个工序过程上能量流的输入与输出过程，以及钢铁生产供应链上能源的整体流动过程。研究钢铁供应链上能源的优化问题，就是研究如何控制此钢铁供应链能源流模型上能源的合理流动与配置。钢铁供应链上的能源优化，主要从降低能耗和节约钢铁产品的能源成本两方面设定对应的目标函数，并从能源需求、能源平衡、废物排放、参数取值等方面考虑规划约束。鉴于钢铁供应链能源优化过程中存在大量的复杂性和不确定性问题，且该优化模型的目标函数和约束条件的系数中存在很多不确定性实数表达。本文将区间数引入到该问题中，用区间系数来统一表达不确定性信息，建立区间数多目标优化模型，从而便于后续运用区间数线性规划方法对模型进行求解。区间数中的区间可以表示为或，表示数在它的概率分布未知时，能取到最大值和最小值[12]。

1.2.1目标函数

对于钢铁企业，其生产供应链上的能源优化，主要以降低能耗和节约能源成本两个目标为主。能耗的降低，主要来源于两个方面：一是工艺流程和生产技术的改进，降低了对单位产品能源的消耗量；二是二次能源的回收利用，用二次能源来补充对一次能源的消耗，本文主要是考虑二次能源的回收利用对能耗的实际影响。能源成本的节约，主要因为二次能源的单位成本要显著低于一次能源的单位成本，故二次能源的回收利用能达到节约能源成本的目标。分别以能耗最小化和能源成本最小化为目标构建钢铁供应链能源优化的目标函数，具体如下：

1）钢铁供应链能耗最小化。以生产单位钢铁产品为基准，单个过程的能耗量为该过程产品量与单位过程产品所消耗能量的乘积。由于该钢铁供应链上存在二次能源流，则单个过程的能耗量，应为从外界输入到该过程的燃料、电力等总能量，与该过程回收并用于其他过程余能的实际差值。对于钢铁供应链上的总能耗，即为所有单个过程能耗之和。钢铁供应链能耗最小化目标函数为：

2）钢铁产品的能源成本最小化。能源成本是以单位能源的平均成本为基准，分为一次能源平均成本和二次能源平均成本，由于市场变化的不确定性，分别用模糊区间、表示，则生产单位钢铁产品的能源成本最小化的目标函数为：

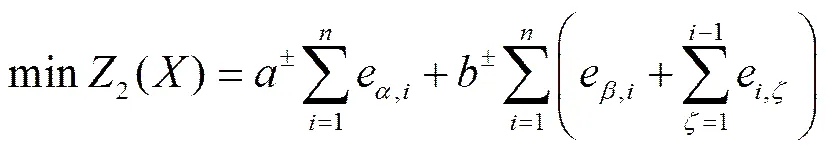
1.2.2 约束条件

钢铁供应链能源优化要实现上述两个优化目标，必须要满足一定的约束条件。这些约束主要包括：钢铁产品生产对能源的基本需求约束，能量的输入与输出的平衡约束，CO等废弃物的排放约束，生产能力与能量排放的边界约束，参数为非负的参数约束，以及其他关系式约束等，具体如下：

1）需求约束：是指钢铁供应链上每个过程的能源供给必须满足过程产品能源的基本需求，即：

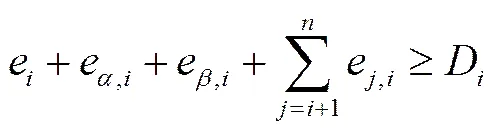
2）能量平衡约束：根据能量守恒定律，每个过程中能量输入与能量输出应保持平衡，即：

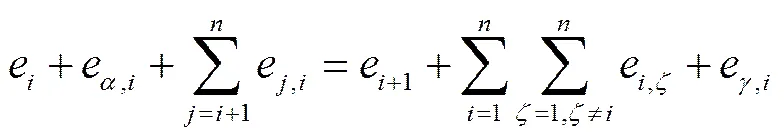
3）排放约束：钢铁供应链上使用了大量的含碳能源，造成生产过程损失的能量中含有CO等温室气体，国家相关部门对钢铁供应链上各过程CO的排放量有明确的排放限值：

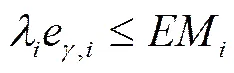
4）边界约束：由于受设备、人员、场地等生产条件的限制，每个生产过程所产出的能量必定不会超出既定的生产能力，即：

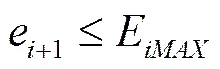
能量排放是不可避免的，每个过程都会产生一定的能量排放，且排放的能量也存在一个最低的排放界限，即：

（7）

（9）

6）参数约束：是对相关变量为非负的参数约束。

本文研究的钢铁供应链能源优化问题属于典型的多目标优化问题（Multi-objective Optimization Problems，MOPs），且上述构建的模型亦为多目标优化模型，存在能耗最小化和能源成本最小化两个目标函数，这两个目标函数存在着相互影响和制约，甚至某种情况下，存在着一定的冲突。因此，与单目标优化模型存在唯一确定的最优解不同的是，多目标优化模型存在一个广义上的优化解，这个优化解通常是一个解集（或称为Pareto解集）。

为了求解上述构建的钢铁供应链能源优化多目标模型，本文介绍一种将-约束法与区间数线性规划方法相结合的求解方法。求解思路为：首先，运用-约束法将本文构建的钢铁供应链能源优化模型中的多目标优化问题转化为单目标优化问题，即将钢铁供应链多目标优化模型转化为单目标优化模型；其次，运用区间数线性规划对转化后的单目标优化模型进行求解，区间数线性规划方法能够有效地处理优化模型中目标函数系数和约束条件系数中存在的区间数表达问题。接下来，分别详细介绍-约束法和区间数线性规划方法的主要思想、求解的主要流程与关键步骤。

在本文构建的钢铁供应链能源优化模型中，我们考虑将能耗最小化目标作为相对重要的目标，因此，运用-约束法求解的思想为将成本最小化目标辅加一个限制域，转变为能耗最小化目标函数的约束条件，从而将钢铁供应链能源优化模型中的多目标优化转化为单目标优化问题，具体步骤如下：

Step2：确定单位钢铁产品能源成本最小化目标函数的限制域取值范围。对于，其不但要满足，且须满足，因此，。

2.2 区间数线性规划求解转化后的钢铁供应链能源单目标优化模型

区间数线性规划（Interval Linear Programming，ILP），是一种用区间系数来解决目标函数和约束条件中信息未知、信息不确定等问题的有效方法，将目标函数和约束条件中决策变量的系数统一转化成区间系数表示[17-20]。基于ILP，将原模型转化为如下所示：

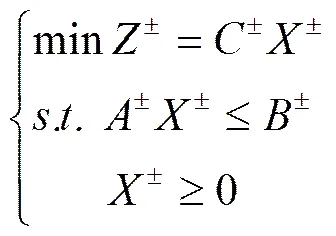
根据文献[21]的研究，区间数线性规划模型可以转化为两个确定性的子模型，这两个子模型分别对应于目标函数的上界和下界。假设，，首先，在模型（Ⅰ）的基础上构建并求解一个对应于的子模型（Ⅱ），其次，在子模型（Ⅱ）解的基础上构建对应于的子模型（Ⅲ）。

对于区间数线性规划问题，存在区间解与区间目标值。为求解以上优化问题，根据文献[21]的引理（2）、定理（2）、推论（3）与推论（5），设计区间数线性规划的求解算法如下：

Step1：构造目标函数的下界子模型（Ⅱ），如下所示：

Step3：求解子模型（Ⅱ）的目标值，公式如下：

Step4：构造子模型（Ⅲ），如下所示：

（模型（Ⅲ））

其中，约束3与约束4是在满足以下两个条件下新增加的约束：1），且；2）子模型（Ⅱ）存在上述满意解：与

Step5：求解子模型（Ⅲ）。同理，求得模型（Ⅲ）存在满意解与。

Step6：求解子模型（Ⅲ）的目标值。公式如下：

Step7：综合step（1）-step（6），我们得知：优化模型的区间解、区间目标值分别为：和。

3算例分析

以国内某大型钢铁企业为例，结合本文构建的能源优化模型，对该企业2010年能源流情况进行实证分析。该钢铁企业主要生产热轧钢板，其工艺生产流程主要包括原材料采集、炼铁、炼钢、轧钢与产品使用等5个过程，含碳等能源经过一系列加工、转换环节到能源产品或排放物，形成该钢铁企业供应链上的能源流网络。

通过调研得知，一方面，该企业钢铁能耗处于全国中下水平，能源利用效率较差；另一方面，该企业能源费用约占钢铁生产成本的1/3，能源费用占比较高。能耗较高与能源成本较大成为该企业近期遇到到发展瓶颈问题，困扰着该钢铁企业的发展。为测试和验证本文所构建的能源优化模型的优化效果，选取该企业2010年能源利用的相关数据进行实证分析。

3.1 优化模型确定

1）目标函数系数

表1 目标函数的系数

分析该钢铁企业供应链的工序过程可知，其过程1、过程2与过程3上存在能源流，过程1、过程2与过程3上的过程产品量分别为：铁矿石与钢板比、铁水与钢板比及钢水与钢板比；其能源成本由基础能源成本与二次能源成本组成。由该钢铁企业2010年度能源利用总结报告，以及搜集到的数据，可得出该钢铁企业2010年度能源优化模型中目标函数的系数如表1所示。其中，铁矿石与钢板比、铁水与钢板比、钢水与钢板比为确定性实数，且都取自该钢铁企业的年度平均值；基础能源成本、二次能源成本为不确定性系数，用区间数表示。本文将基础能源与二次能源的成本区间定义为：与分别取该钢铁企业2010年的年度平均值，与分别取2010年度钢铁行业基础能源成本与二次能源成本的最大值。

2）约束条件系数

表2约束条件的系数

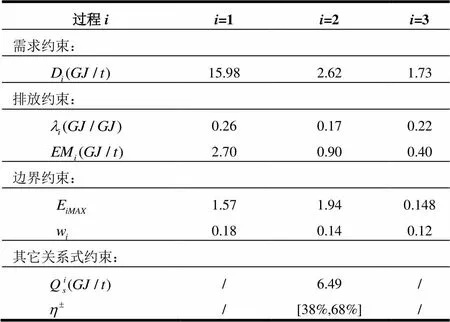
过程ii=1i=2i=3 需求约束： 15.982.621.73 排放约束： 0.260.170.22 2.700.900.40 边界约束： 1.571.940.148 0.180.140.12 其它关系式约束： /6.49/ /[38%,68%]/

3）优化模型

分表将表1中目标函数的系数和表2中约束条件的系数代入到公式（1）-（10）中，得到本案例的具体优化模型如下：

表1某钢铁企业2010年度钢铁供应链能源优化前后能耗与成本比较

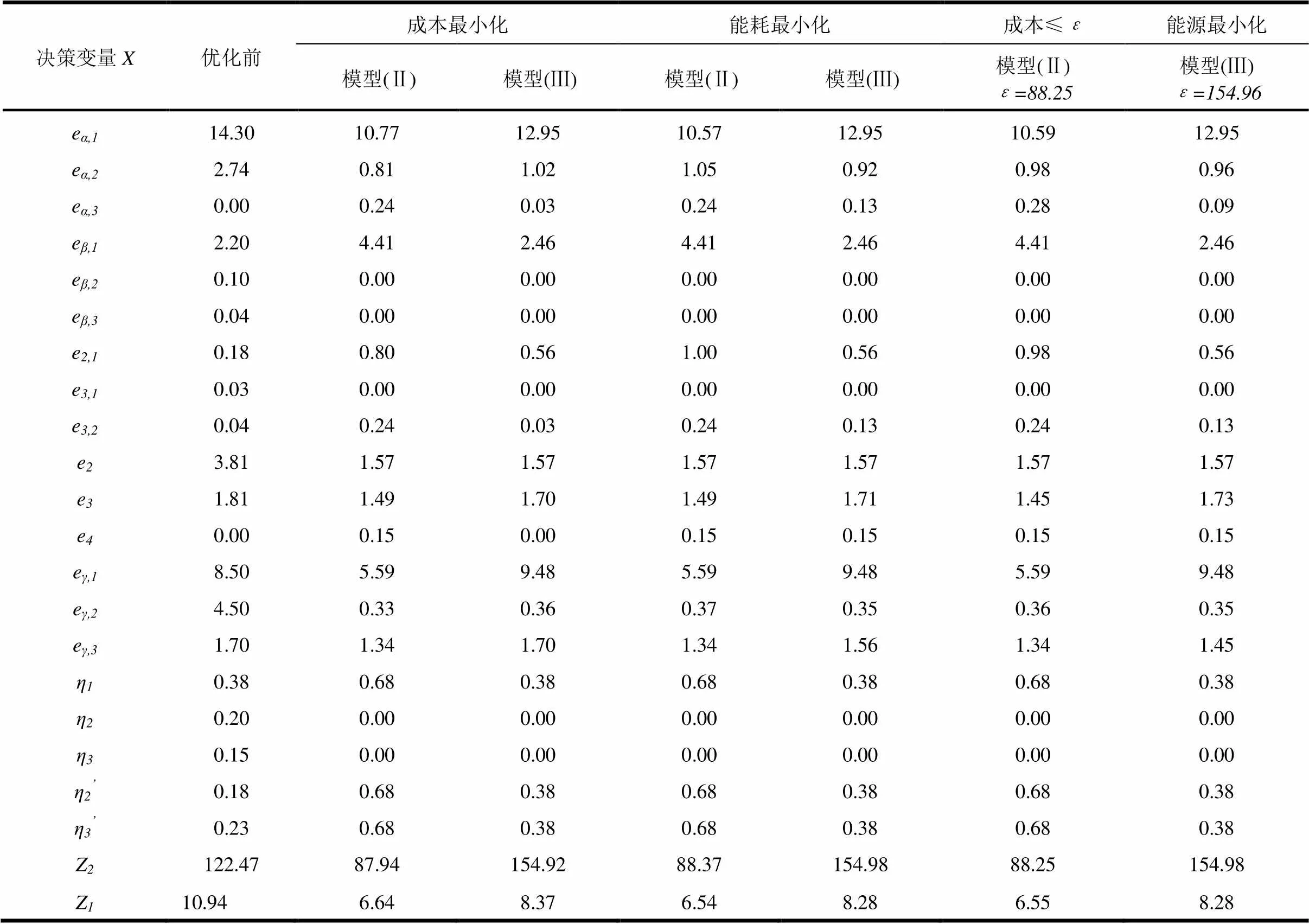
决策变量X优化前成本最小化能耗最小化 成本≤ε 能源最小化 模型(Ⅱ)模型(Ⅲ)模型(Ⅱ)模型(Ⅲ)模型(Ⅱ)ε=88.25模型(Ⅲ)ε=154.96 eα,114.3010.7712.9510.5712.9510.5912.95 eα,22.740.811.021.050.920.980.96 eα,30.000.240.030.240.130.280.09 eβ,12.204.412.464.412.464.412.46 eβ,20.100.000.000.000.000.000.00 eβ,30.040.000.000.000.000.000.00 e2,10.180.800.561.000.560.980.56 e3,10.030.000.000.000.000.000.00 e3,20.040.240.030.240.130.240.13 e23.811.571.571.571.571.571.57 e31.811.491.701.491.711.451.73 e40.000.150.000.150.150.150.15 eγ,18.505.599.485.599.485.599.48 eγ,24.500.330.360.370.350.360.35 eγ,31.701.341.701.341.561.341.45 η10.380.680.380.680.380.680.38 η20.200.000.000.000.000.000.00 η30.150.000.000.000.000.000.00 η2’0.180.680.380.680.380.680.38 η3’0.230.680.380.680.380.680.38 Z2122.4787.94154.9288.37154.9888.25154.98 Z110.946.648.376.548.286.558.28

3.2 优化模型求解

根据钢铁企业2010年度能源利用总结报告可知，该企业2010年全年平均吨钢综合能耗为10.94，平均吨钢能源成本为122.47。各个工序环节以稳定的能源流分配方式进行生产，能源流平均输入、输出都有详细的报告值，优化前各个生产工序的能源流配置情况如表3所示。

将表1和表2中各变量的参数值分别代入公式（1）-（10），即可得到该钢铁企业供应链能源优化模型，再运用本文设计的基于-约束与区间数线性规划模型求解方法，编程求解该算例，得到优化该模型的求解结果见表3。由表3可知，该钢铁企业供应链能源优化模型的最终满意解为：当=88.25，=154.96时，，。

3.3 优化结果分析

由表3求得的该钢铁企业2010年度钢铁供应链能源优化结果，我们可以得出以下结论：

1）通过能源的优化配置，减少了该钢铁企业工序过程中外界能量的输入，提高了二次能源的回收利用率。如：对于过程1-炼铁，优化后，从外界输入的能量、本过程流入过程2-炼钢的能量及散发到外界的能量减少，回收自用的能量和从后续过程回收的能量增加；对于过程2-炼钢，从外界输入的能量、本过程流入过程3-轧钢的能量及散发到外界的能量减少，回收自用的能量减至零，回收的余热余能主要用于其它过程，过程中的二次能源主要来源于过程3-轧钢回收的二次能量；对于过程3-轧钢，回收自用的余热余能也为零，该过程的能量主要来自于上一过程带入的能量，过程散失到外界的能量也比优化前有明显减小。

2）通过二次能源的优化利用，一方面，该钢铁企业2010年度总能耗从优化前的10.94降低到6.55～8.28，节能效率达到24.31%～40.13%，能耗优化效果显著；另一方面，该钢铁企业2010年度总能源成本从122.47降低到88.25，节约率达到27.94%，节约了该钢铁企业的能源成本。

3）能源优化模型具有相对稳定性。在求解能源优化模型的过程中，不难发现，在初始阶段能耗降低会伴随着能源成本的增加，但当能耗降到最优值时，能源成本对能耗的影响较小，能耗保持相对稳定的状态。

模型求解结果显示，钢铁企业生产供应链上的能源流通过优化，可以有效地降低生产供应链上能源的消耗和能源利用的经济成本。这是由于：一方面，二次能源的回收利用（自用和他用），极大地补充了供应链上能源的需求，减少了对一次能源的消耗，因此使得总能耗降低；另一方面，通过表2可以看出，一次能源的成本为[7.07,10.8]，而二次能源的成本仅为[0.80,1.20]，二次能源的使用成本要远低于一次能源的使用成本，因此，二次能源的回收利用（自用和他用）必然能降低供应链上整体能源消费成本。故模型求解结果具有一定合理性。

4总结

论文首先分析了钢铁企业生产供应链系统上能源的流动过程，建立了钢铁供应链能源流模型，在此基础上构建了考虑能耗成本最小化、能源成本最小化双重目标及多个复杂约束共作用下的钢铁供应链能源优化模型。其次，设计了一种基于-约束法和区间数线性规划方法的求解模型，给出了详细的求解过程。最后，结合国内某大型钢铁企业2010年的能源利用的相关数据进行实证分析，实证结果显示：1）二次能源的回收自用或他用，可以补充对一次能源的消耗，从而切实减少外界能源的输入；2）若该钢铁企业能按模型所要求的强化二次能源的有效回收利用，则其2010年能源效率将会提高到124.31%～140.13%，能源成本将会降低27.94%；3）数据显示本文构建的优化模型具有一定的稳定性。案例从实证的角度验证了本文构建的模型具有一定的有效性和实用性。在后续的研究中，将努力收集更多的案例进行实证研究，以对模型就行修正和完善，并争取在部分钢铁企业中进行应用实践。

[1] Kong H, Qi E, Li H, et al. An MILP model for optimization of byproduct gases in the integrated iron and steel plant [J]. Applied Energy, 2010,87:2156–2163.

[2] Sandhu MA, Helo P, Kristianto Y. Steel supply chain management by simulation modeling [J]. Benchmarking: An International Journal, 2013,20:45–61.

[3] Jiang G, He E, Li G, et al. Production line production planning model of iron and steel enterprise [J]. Journal of Digital Information Management, 2013,11:131–135.

[4] Potter A, Mason R, Naim M, et al. The evolution towards an integrated steel supply chain: A case study from the UK [J]. International Journal of Production Economics, 2004,89:207–216.

[5] Zäpfel G, Wasner M. Warehouse sequencing in the steel supply chain as a generalized job shop model [J]. International Journal of Production Economics, 2006,104:482–501.

[6] Wei Y-M, Liao H, Fan Y. An empirical analysis of energy efficiency in China’s iron and steel sector [J]. Energy, 2007,32:2262–2270.

[7] Michaelis P, Jackson T. Material and energy flow through the UK iron and steel sector. Part 1: 1954–1994 [J]. Resources, Conservation and Recycling, 2000,29:131–156.

[8] Michaelis P, Jackson T. Material and energy flow through the UK iron and steel sector: Part 2: 1994–2019 [J]. Resources, Conservation and Recycling, 2000,29:209–230.

[9] Cai YP, Huang GH, Yang ZF, et al. Identification of optimal strategies for energy management systems planning under multiple uncertainties [J]. Applied Energy, 2009,86:480–495.

[10] Yu Q, Lu Z, Cai J. Calculating Method for Influence of Material Flow on Energy Consumption in Steel Manufacturing Process [J]. Journal of Iron and Steel Research, International, 2007,14:46–51.

[11] Andersen JP, Hyman B. Energy and material flow models for the US steel industry [J]. Energy, 2001,26:137–59.

[12] 刘新旺, 达庆利, 韩世莲. 区间数运输问题模型及其模糊目标规划求解方法[J]. 管理工程学报, 1999,13:6–8.

[13] George Mavrotas. Effective implementation of the ε-constraint method in Multi-Objective Mathematical Programming problems [J]. Applied Mathematics and Computation, 2009,213:455–465.

[14] Ehrgott M, Ruzika S. Improved ε-Constraint Method for Multiobjective Programming [J]. Journal of Optimization Theory and Applications, 2008,138:375–396.

[15] Esmaili M, Amjady N, Shayanfar HA. Multi-objective congestion management by modified augmented ε-constraint method [J]. Applied Energy, 2011,88:755–766.

[16] Laumanns M, Thiele L, Zitzler E. An efficient, adaptive parameter variation scheme for metaheuristics based on the epsilon-constraint method [J]. European Journal of Operational Research, 2006, 169: 932 – 942.

[17] Alolyan I. Algorithm for interval linear programming involving interval constraints [C]. IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), 2013 Joint, 2013, p. 1274–1278.

[18] Dong C, Huang GH, Cai YP, et al. An interval-parameter minimax regret programming approach for power management systems planning under uncertainty [J]. Applied Energy, 2011,88:2835–2845.

[19] Dai C, Li YP, Huang GH. An interval-parameter chance-constrained dynamic programming approach for capacity planning under uncertainty [J]. Resources, Conservation and Recycling, 2012, 62: 37 – 50.

[20] 樊治平, 胡国奋. 区间数多属性决策的一种目标规划方法 [J]. 管理工程学报, 2000,14:50–53.

[21] Huang GH, Baetz BW, Patry GG. Grey integer programming: An application to waste management planning under uncertainty [J]. European Journal of Operational Research, 1995,83:594–620.

An Energy Optimization Model of Iron and Steel Supply Chain Using-Constraint Method and Interval Linear Programming Approach

ZHU Xiao-long1,2, DING Shuai1, ZHU Wei-dong1, PENG Zhang-lin1, NI Da-wei1

（1. School of Management, Hefei University of Technology, Hefei 230009, China; 2 .Anhui Business Vocational College, Hefei 231131, China）

The production system of iron and steel enterprises can be conceptualized into two processes: material flow transformation and energy flow transformation. The operation of these two processes consumes a great amount of resource, energy consumption and waste emissions. Due to the generation of secondary energy, energy flow in the iron and steel supply chain interacts among different production processes and runs forward and backward respectively, which has an important impact on the energy utilization for an iron and steel enterprise. Therefore, it is necessary to study the energy optimization of an iron and steel supply chain from the perspective of secondary energy recycling with the aim of reducing energy consumption and energy costs in the supply chain and improving energy efficiency through the optimal allocation of secondary energy.

In order to clarify the flowing process of secondary energy in an iron and steel supply chain as well as the actual impact of secondary energy recycling on energy optimization of the iron and steel supply chain, an energy optimization model is proposed based on the detailed analysis of energy flows. Then, the-constraint method and interval linear programming approach are introduced to the process of solving the model. Finally, the research result that the model can effectively reduce the energy consumption of an iron and steel enterprise and improve energy utilization efficiency has been demonstrated through a typical case study. This paper is composed of the following four parts:

Firstly, this paper analyzes the energy flow in an iron and steel supply chain. There are 7 strands of energy flows in a single process: (1) the energy input from the upstream; (2) the energy output from the present process; (3) the energy input from the outside; (4) the wasted energy; (5) the recycling energy for own use; (6) the recycling energy for others’ use; and (7) the energy reversing from the downstream process. Energy flow in all single process can be integrated into a more complicated energy flow network system. It is clear that the energy flows not only in a single process but also in different processes in upstream and downstream activities.

Secondly, an energy optimization model is constructed in this paper. The interval coefficients are used to express uncertain information of the objective function and its constraints. A multi-objective optimization model for an iron and steel supply chain is constructed. The objective function includes energy consumption minimization and energy cost minimization. The related constraints include basic demands for energy when producing iron and steel products, conserving input energy and output energy, requiring production capacity and technical parameters, increasing energy efficiency of a cogeneration system, demanding limits for secondary energy, having a constraint for the amount of electric output and emission limits, such as CO2, and non-negativity for some parameters.

Thirdly, the solution based on-constraint method and interval linear programming is given. We change a multi-objective optimization problem into a single-objective optimization problem using-constraint method. A single-objective optimization model for an iron and steel supply chain is changed from a multi-objective optimization model. We solve the single-objective optimization model using interval linear programming.

Finally, this paper implements a deeply empirical analysis based on a large Chinese iron and steel enterprise. There are three findings in this study. First, the energy from the outside has been reduced, and the efficiency for recycling secondary energy has been improved. Second, by optimization of secondary energy, the total annual energy consumption is reduced from 10.94GJ/t-steel to 6.55~8.28GJ/t-steel in 2010, and the efficiency of energy conservation is about 24.31%~40.13%. Thus, the result is quite significant. On the other hand, the total energy cost is decreased from 122.47USD/t-steel to 88.25USD/t-steel in 2010. The savings rate reaches up to 27.94%. It helps enterprises to economize the energy cost. Third, the energy optimization model has a relatively stability.

In summary, we can optimize resource and energy allocation using the constructed energy optimization model of iron and steel supply chain that is based on-constraint method and interval linear programming approach. In addition, we can improve the awareness to recycle the secondary energy. All of these measures can reduce the energy consumption from the outside and improve the efficiency for recycling secondary energy in an iron and steel supply chain. Thus, for an iron and steel enterprise the efficiency of energy conservation could be improved and the energy cost could be reduced. Therefore, an enterprise should adjust their supply chain systems to strengthen the recycling and utilization of secondary energy by optimizing and improving their manufacturing process.

iron and steel supply chain; energy optimization; interval linear programming;-constraint method

中文编辑：杜 健；英文编辑：Charlie C. Chen

TF 4

A

1004-6062(2016)02-0243-08

10.13587/j.cnki.jieem.2016.02.030

2012-11-01

2014-01-03

国家自然科学基金资助项目（71201042，71071045），安徽高校人文社科研究基地资助项目（2012AJRW0293）

朱小龙（1976—），男，安徽合肥人，副教授，博士研究生，研究方向：能源管理、决策分析。